73.矩陣清零

題目

給定一個 *m* x *n* 的矩陣，如果一個元素為 0 ，則將其所在行和列的所有元素都設為 0 。請使用 原地 算法。

示例 1：

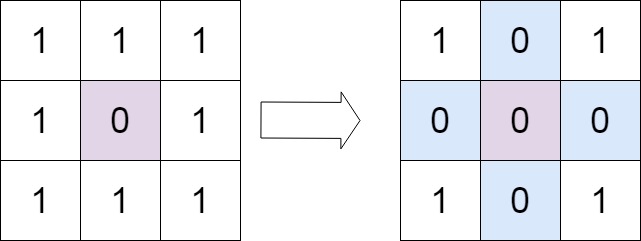
輸入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
輸出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

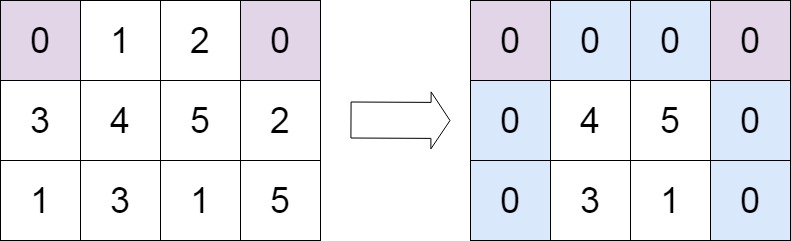
輸入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]

思路

第一次把滿足條件的行和列用set存下來，第二次遍歷即可，O(n^2)

代碼如下：

class Solution {
public:void setZeroes(vector<vector<int>>& matrix) {unordered_set<int> a,b;for(int i = 0;i<matrix.size();i++){for(int j = 0;j<matrix[0].size();j++){if(matrix[i][j] == 0){a.insert(i);b.insert(j);}}}for(int i = 0;i<matrix.size();i++){for(int j = 0;j<matrix[0].size();j++){if(a.count(i) != 0 || b.count(j) != 0){matrix[i][j] = 0;}}}}
};

54.螺旋矩陣

題目

給你一個 m 行 n 列的矩陣 matrix ，請按照 順時針螺旋順序 ，返回矩陣中的所有元素。

示例 1：

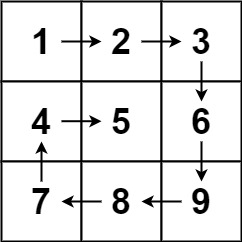
輸入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
輸出：[1,2,3,6,9,8,7,4,5]

示例 2：

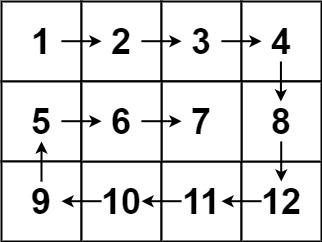
輸入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
輸出：[1,2,3,4,8,12,11,10,9,5,6,7]

思路

這個應該是很常見的一道題了，，，感覺頻率很高，我習慣了一套模板就是把left，right，top和button確定下來，然后從左到右，從上到下，從右往左，從下往上遍歷即可

代碼如下：

class Solution {
public:vector<int> spiralOrder(vector<vector<int>>& matrix) {int left = 0,right = matrix[0].size()-1;int top = 0,button = matrix.size()-1;vector<int> ans;while(true){for(int i = left;i<right+1;i++){ans.emplace_back(matrix[top][i]);}top++;if(top > button) break;for(int i = top;i<button+1;i++){ans.emplace_back(matrix[i][right]);}right--;if(right < left) break;for(int i = right;i>left-1;i--){ans.emplace_back(matrix[button][i]);}button--;if(button < top) break;for(int i = button;i>top-1;i--){ans.emplace_back(matrix[i][left]);}left++;if(left > right)break;}return ans; }
};

48.旋轉圖像

題目

給定一個 n × n 的二維矩陣 matrix 表示一個圖像。請你將圖像順時針旋轉 90 度。

你必須在?原地 旋轉圖像，這意味著你需要直接修改輸入的二維矩陣。請不要 使用另一個矩陣來旋轉圖像。

示例 1：

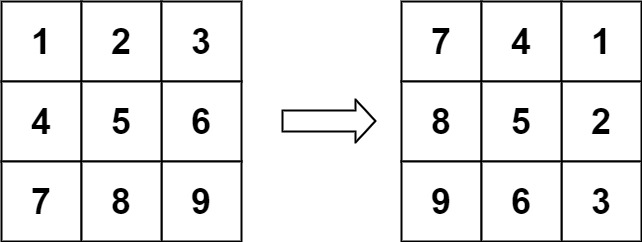
輸入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
輸出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

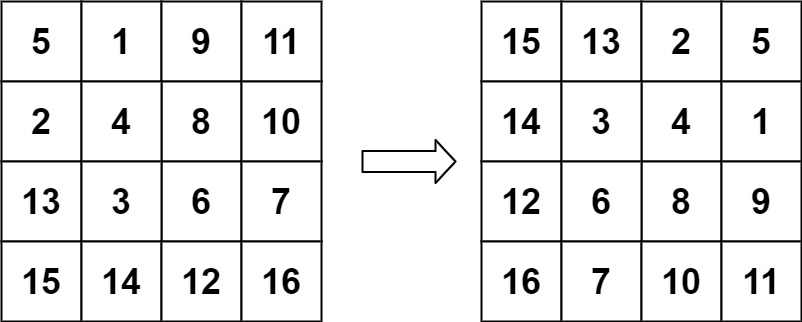
輸入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
輸出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

思路

因為不能使用另一個矩陣來記錄，事實上很容易發現下標規律是[i,j] -> [j,n-1-i]，不過其實可以上下翻轉一次再左上角和右下角翻轉一次會是同樣的效果，O(n^2)

代碼如下：

class Solution {
public:void rotate(vector<vector<int>>& matrix) {for(int i = 0;i<matrix.size()/2;i++){for(int j = 0;j < matrix[0].size();j++){int tmp = matrix[i][j];matrix[i][j] = matrix[matrix.size()-1-i][j];matrix[matrix.size()-1-i][j] = tmp;}}for(int i = 0;i<matrix.size();i++){for(int j = i+1;j<matrix[0].size();j++){swap(matrix[i][j],matrix[j][i]);}}}
};

240.搜索二維矩陣II

題目

編寫一個高效的算法來搜索 *m* x *n* 矩陣 matrix 中的一個目標值 target 。該矩陣具有以下特性：

• 每行的元素從左到右升序排列。

• 每列的元素從上到下升序排列。

示例 1：

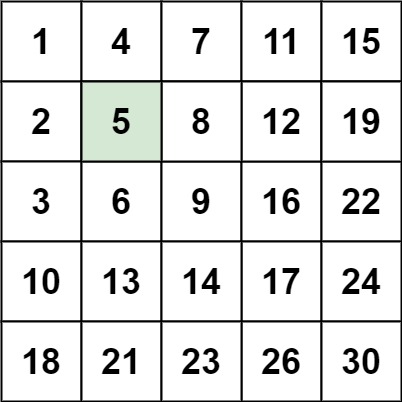
輸入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
輸出：true

示例 2：

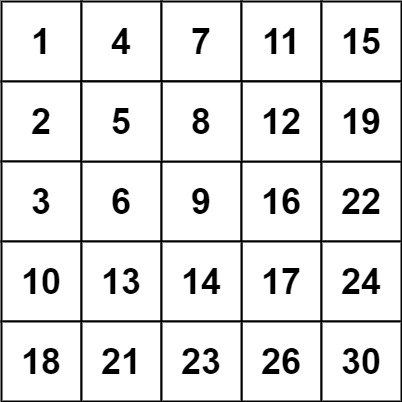
輸入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
輸出：false

思路

發現規律，從右上角觀察發現，利用i和j的加和減可以遍歷整個矩陣

如果找到則返回true即可

代碼如下：

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int n = matrix.size();int m = matrix[0].size();int i = 0,j = m-1;while(i < n && j > -1){if(matrix[i][j] < target) i++;else if(matrix[i][j] > target) j--;else{return true;}}return false;}
};