前綴和算法：提升編程效率的秘密武器(Java版)

本篇會加入個人的所謂魚式瘋言

??????魚式瘋言:??????此瘋言非彼瘋言
而是理解過并總結出來通俗易懂的大白話,
小編會盡可能的在每個概念后插入魚式瘋言,幫助大家理解的.
🤭🤭🤭可能說的不是那么嚴謹.但小編初心是能讓更多人能接受我們這個概念 ！！！

在這里插入圖片描述

前言

在前面我們熟悉了 == “雙指針” 算法== ，== “滑動窗口” 算法==， 以及 二分查找 算法 。 小伙伴可以思考下，

這些本質上是不是都是雙指針呢， 沒錯，當然是的 💖 💖 💖

這三個專題我們已經 圓滿結束啦, 那么我們的雙指針大家族也算是告一段落啦 💖 💖 💖

而在本篇我們中講新的專題，是去雙指針不同的專題 ， 前綴和 算法

下面小伙伴先了解下本篇文章的規劃吧 😊 😊 😊

目錄

  1. 前綴和算法的初識

  2. 前綴和算法的實際運用

  3. 前綴和算法的總結

一. 前綴和算法的初識

<1>. 前綴和算法的簡介

前綴和算法，也稱為 前綴和技巧 ，是一種常見的算法技巧，用于高效地計算數組或序列中某個 位置前 的 所有元素的和。

前綴和算法的思路是先計算出從數組的 起始位置到每個位置 的 子數組和 ，然后根據需要的范圍計算出相應的結果。

<2>. 前綴和使用流程

我們通過一個簡單的題目來講解前綴和的具體使用吧 💖 💖 💖 💖

1. 前綴和

DP34.前綴和題目鏈接

<1>. 題目描述

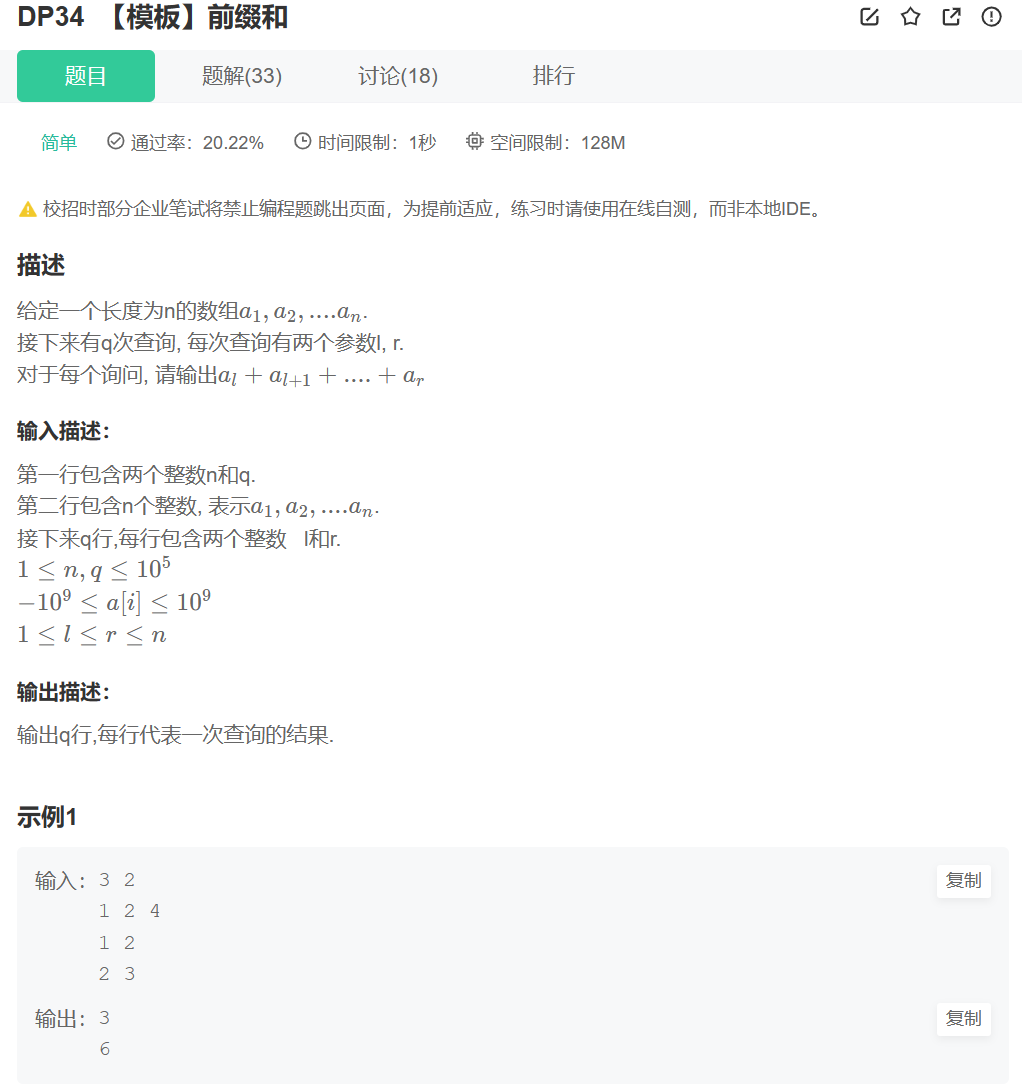
在這里插入圖片描述

題目含義：

先 初始化一個數組，并 指定長度，然后在指定一段需要求的 子數組的區間 的 總和 ，進行返回， 注意這里要指定 q 次, 意味著我們要求 q 次子數組的總和 并返回

<2>. 講解算法思想

題目分析 ：

遇到求某段區間的總和，我們不難想到

解法一 :

暴力求解

用一個 for 循環 來累加 左右區間 的，然后循環往復進步 q 次

前綴和算法 :

我們先定義一個 數組dp，這個數組是主要用來統計 i 位置到 0 的 元素的 總和

算法步驟

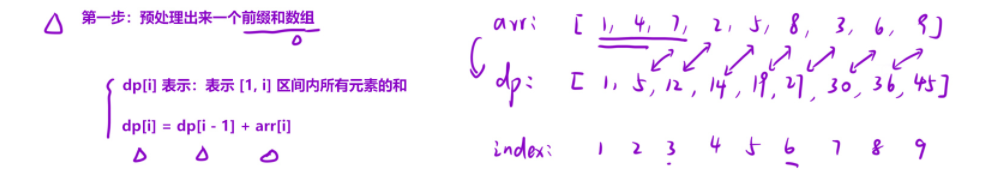
在這里插入圖片描述

  • 第一步： 先定義 dp 數組， i = 0 時，先把 第一個元素 進行 相加， 然后到 i = 1 時，我們就在 dp[0] 的基礎上加上 原數組(假設原數組名為 nums ) nums[1] 那個元素 , 循環往復，意味著就可以得到我們的 每個位置到 0 位置的總和的數據。

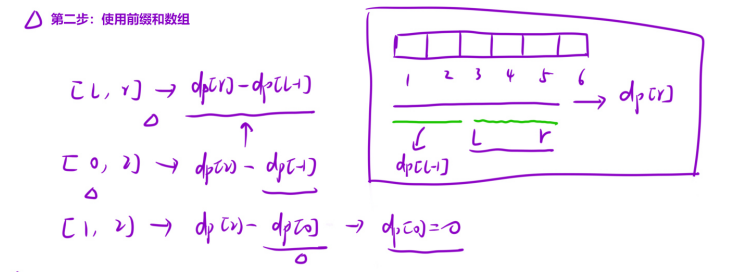
在這里插入圖片描述

  • 第二步： 使用前綴和數組，我們要得到某得區間的，就可以利用前綴和數組，用 dp[右邊界] - dp[左邊界-1] 就可以得到我們的該 區間的和

請添加圖片描述

<3>. 編寫代碼

import java.util.Scanner;// 注意類名必須為 Main, 不要有任何 package xxx 信息
public class Main {public static void main(String[] args) {Scanner in = new Scanner(System.in);int n=in.nextInt();int q=in.nextInt();long [] array=new long [n+1];for(int i =1 ; i < n+1 ; ++i) {array[i]=in.nextInt();      }int k=0;long[] sum=new long[q];long[] dp=new long[n+1];dp[0]=0;for(int x= 1; x < n+1 ; x++ ) {dp[x]= dp[x-1] + array[x];}while(q != 0) {int left = in.nextInt();int right = in.nextInt();System.out.println(dp[right]-dp[left-1]);                k++;q--;}}}

在這里插入圖片描述

魚式瘋言

前綴和算法的時間復雜度為 O(n) ，其中 n 表示數組的長度。

它的主要應用場景包括計算 連續子數組的和 、找到和為某個特定值的 子數組等 。

細節處理 ：

 dp[0]=0;

我們這里就直接放置 下標 0 的位置為 0 ，這樣就可以 有序的進行循環 dp[i]= dp[i-1] +array[i];

在這里插入圖片描述

因為當 i=0 ， i-1 就很有可能 發生越界

二. 前綴和的實際運用

1. 除自身以外的乘積

238.除自身以外的乘積題目鏈接

<1>. 題目描述

在這里插入圖片描述

給你一個整數數組 nums，返回 數組 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘積 。

題目數據 保證 數組 nums之中任意元素的全部前綴元素和后綴的乘積都在 32 位 整數范圍內。

請 不要使用除法，且在 O(n) 時間復雜度內完成此題。

示例 1:

輸入: nums = [1,2,3,4]
輸出: [24,12,8,6]

示例 2:

輸入: nums = [-1,1,0,-3,3]
輸出: [0,0,9,0,0]

題目含義 ：

定義一個新數組，求 nums 除了該 位置以外元素 的 乘積，并賦值給新數組的 當前位置

<2>. 講解算法思想

題目分析 :

因為題目要求我們不能使用 除法 ，

所以就要利用 前綴積 算法, 并且使用 前綴積 和 后綴積 結合起來去解決本題

在這里插入圖片描述

算法步驟

首先我們需要兩個數組一個是前綴積 dpleft 和 dpright ；來 （ 同一下標） 初始化我們的 前綴積 以及 后綴積

當我們定義 前綴積 時 ：

從 下標 0 開始 從左往右 累加 dp[i]= dp[i-1] * nums[i-1] 初始化 deleft數組

請添加圖片描述

當我們定義 后綴積deright 從 nums最后一個數組 從右往左 開始 （同一下標） dp[i] = dp[i + 1] * nums[i + 1] 來初始化 后綴和deright

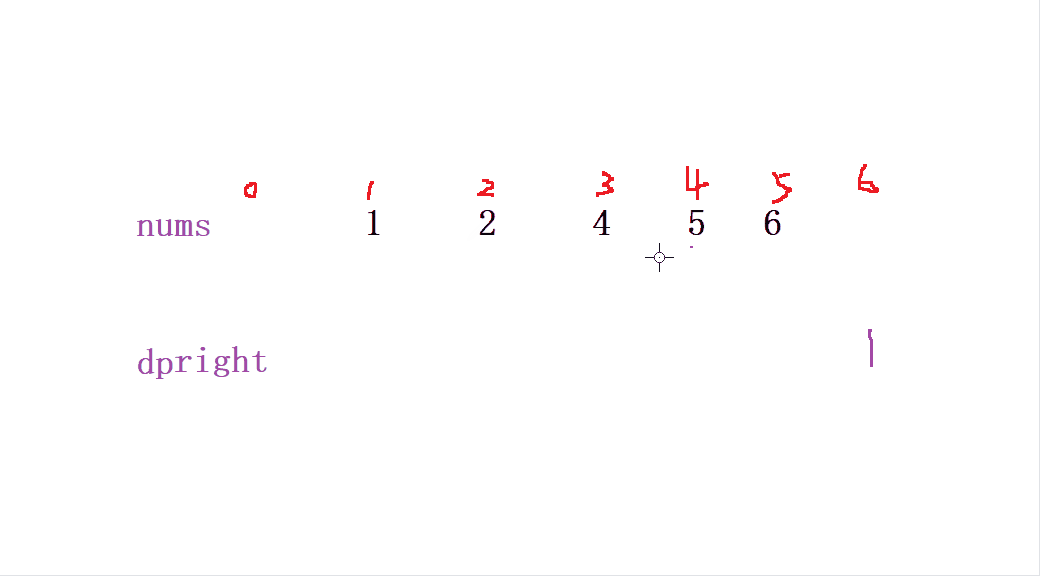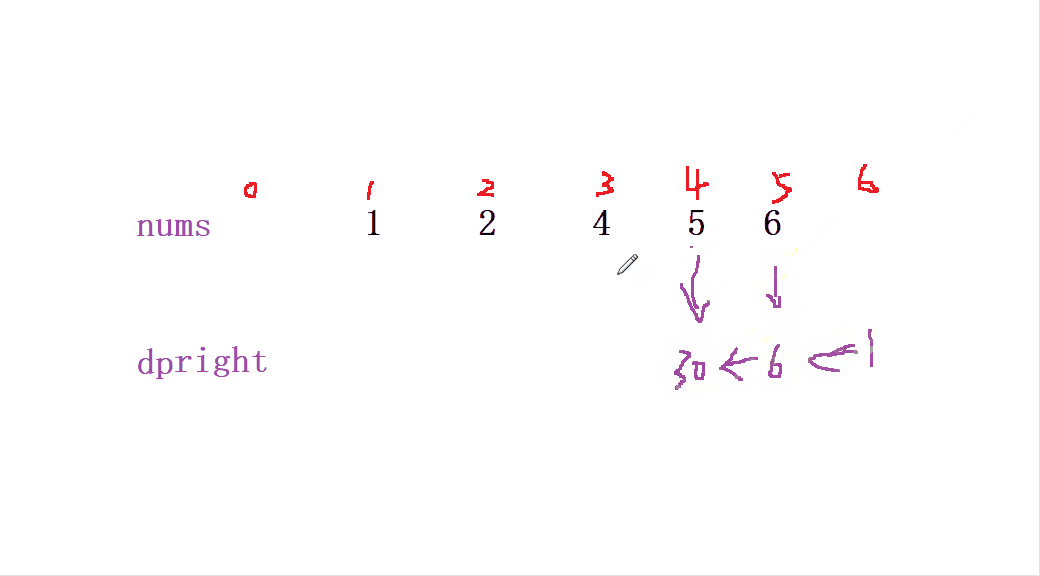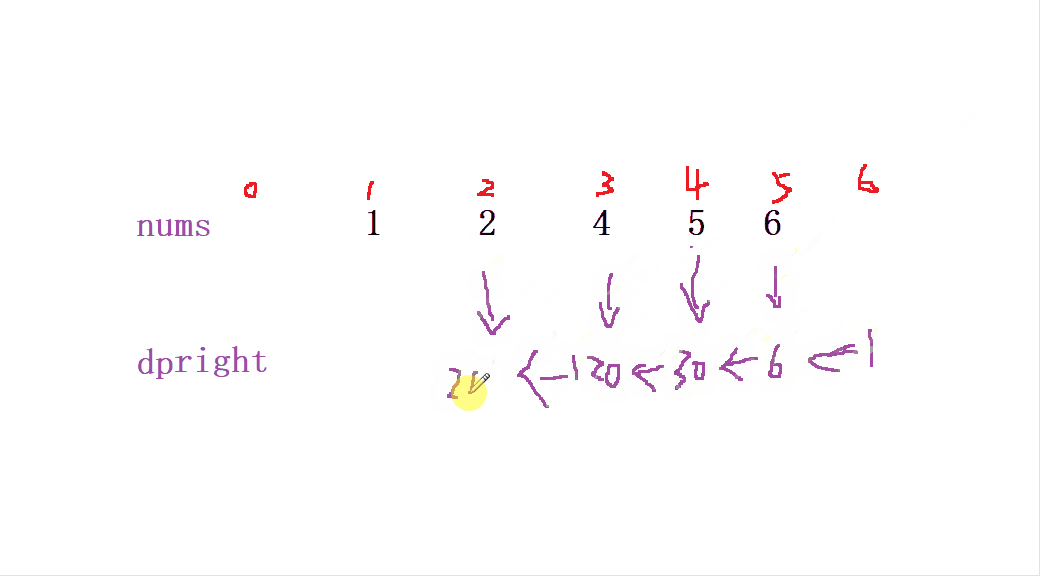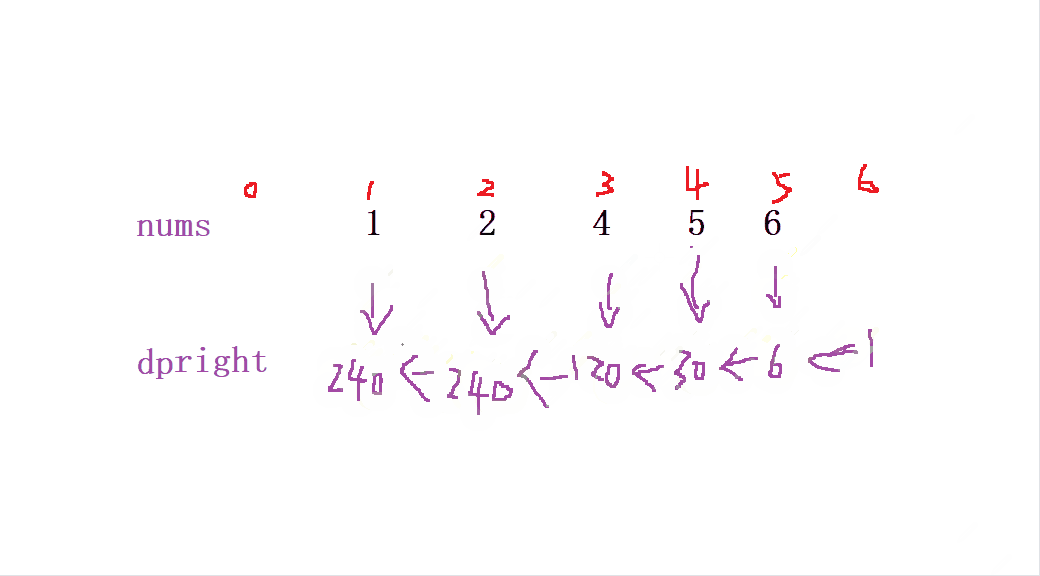
請添加圖片描述

最后我們要獲取到該位置的值就可以 通過 ret[i]= dpleft[i] * dpright[i+1]; 來獲取當前位置除自身以外的 乘積

<3>. 編寫代碼

class Solution {public int[] productExceptSelf(int[] nums) {// 得到數組長度int n= nums.length;// 定義一個前綴積的數組int[] dpleft = new int [n+1];dpleft[0]= 1;// 進行前綴積for(int i =1 ; i < n+1 ; ++i) {dpleft[i]=nums[i-1] * dpleft[i-1];}  // 定義 一個后綴積的數組int[] dpright= new int[n+1];dpright[n]=1;// 進行后綴積的數組for(int  j = n-1 ; j >= 0; j-- ) {dpright[j]= nums[j] * dpright[j+1];}int[] ret= new int[n];// 得到返回值for(int i =0 ; i < n; ++i) {ret[i]= dpleft[i] * dpright[i+1];}return ret;}
}

在這里插入圖片描述

魚式瘋言

本題的一點體會

本題的核心是如何寫出 前綴積數組 和 后綴積的數組 的遞推公式， 以及邊界值的處理細節

邊界處理細節

  // 定義一個前綴積的數組int[] dpleft = new int [n+1];dpleft[0]= 1;// 定義 一個后綴積的數組int[] dpright= new int[n+1];dpright[n]=1;

定義一個比一個原來的數組的長度 +1 的 dp數組，并且把 最邊界 都賦值為 1 (注意是 1， 而不是為 0 )

2. 和可被 k 整除的子數組

974. 和可被 k 整除的子數組題目鏈接

<1>. 題目描述

在這里插入圖片描述

給定一個整數數組 nums 和一個整數 k ，返回其中元素之和可被 k 整除的（連續、非空） 子數組 的數目。

子數組 是數組的 連續 部分。

示例 1：

輸入：nums = [4,5,0,-2,-3,1], k = 5
輸出：7
解釋：
有 7 個子數組滿足其元素之和可被 k = 5 整除：
[4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]

示例 2:

輸入: nums = [5], k = 9
輸出: 0

題目含義 ：

返回一段的所有能夠被 k 整除 的 子數組 的 個數

<2>. 講解算法思想

解法一：

暴力枚舉

解法二：

前綴和

講解 前綴和算法 之前，我們先得熟悉 兩個原理

1. 同余定理

如果 (a - b) % n == 0 ，那么我們可以得到一個結論： a % n == b % n 。

用文字敘述就是，如果 兩個數相減的差能被 n 整除 ，那么這兩個數對 n 取模 的 結果相同。

例如： ·(26 - 2) % 12 == 0 ，那么 26 % 12 == 2 % 12 == 2 。

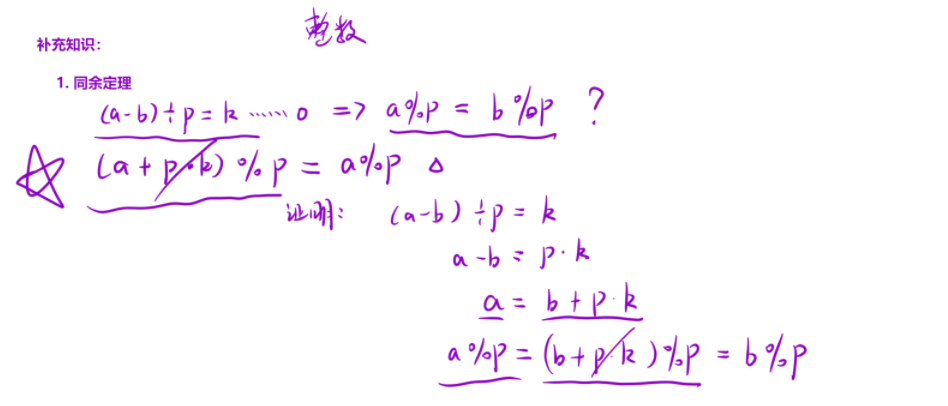
在這里插入圖片描述

2. java 中負數取模的處理方法

a. Java 中關于負數的取模運算，結果是**「把負數當成正數，取模之后的結果加上一個負號」。**

例如： -1 % 3 = -(1 % 3) = -1

b. 因為有負數，為了防止發生 「出現負數」 的結果，以 (a % n + n) % n 的形式輸出 保證為正 。

例如： -1 % 3 = (-1 % 3 + 3) % 3 = 2

在這里插入圖片描述

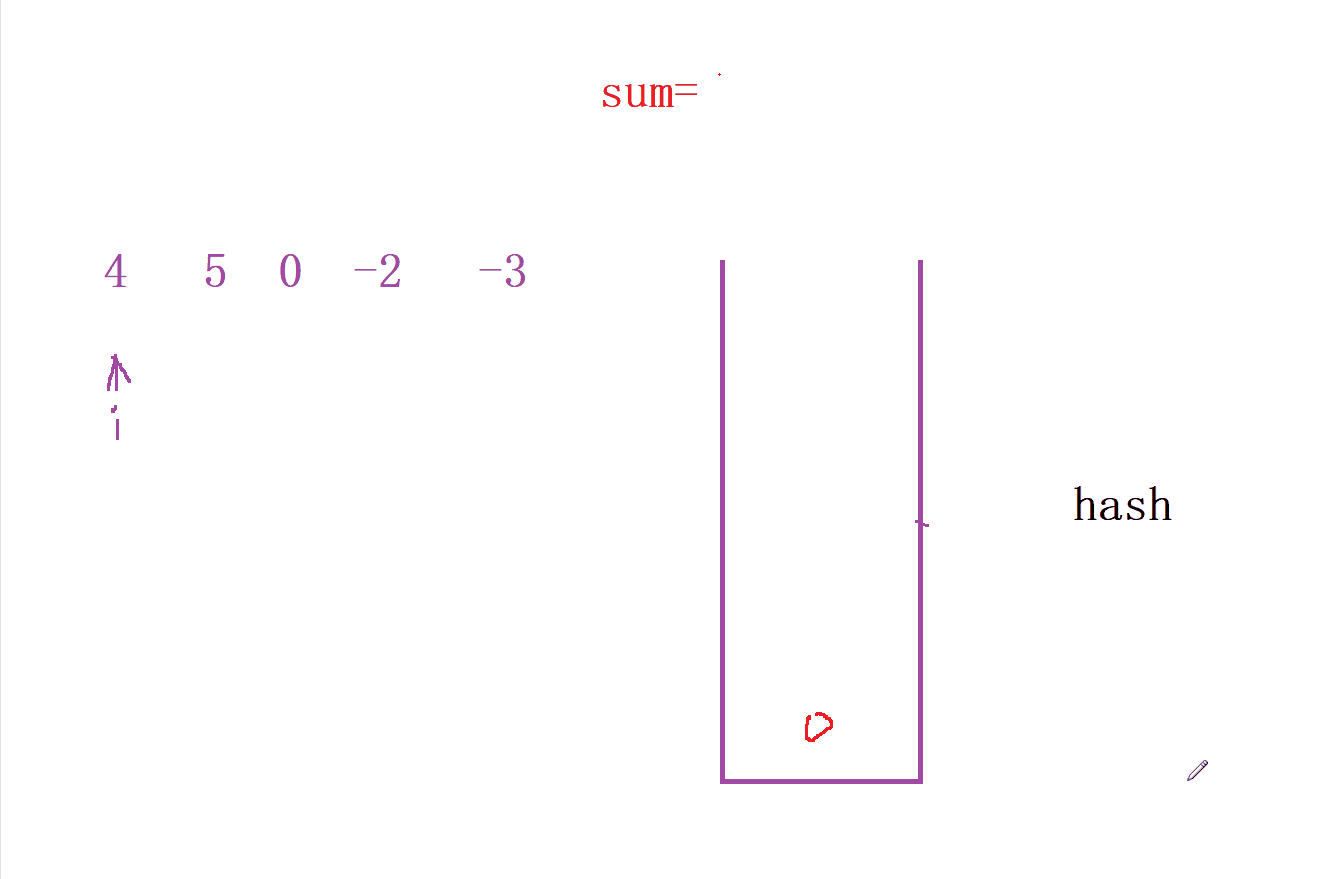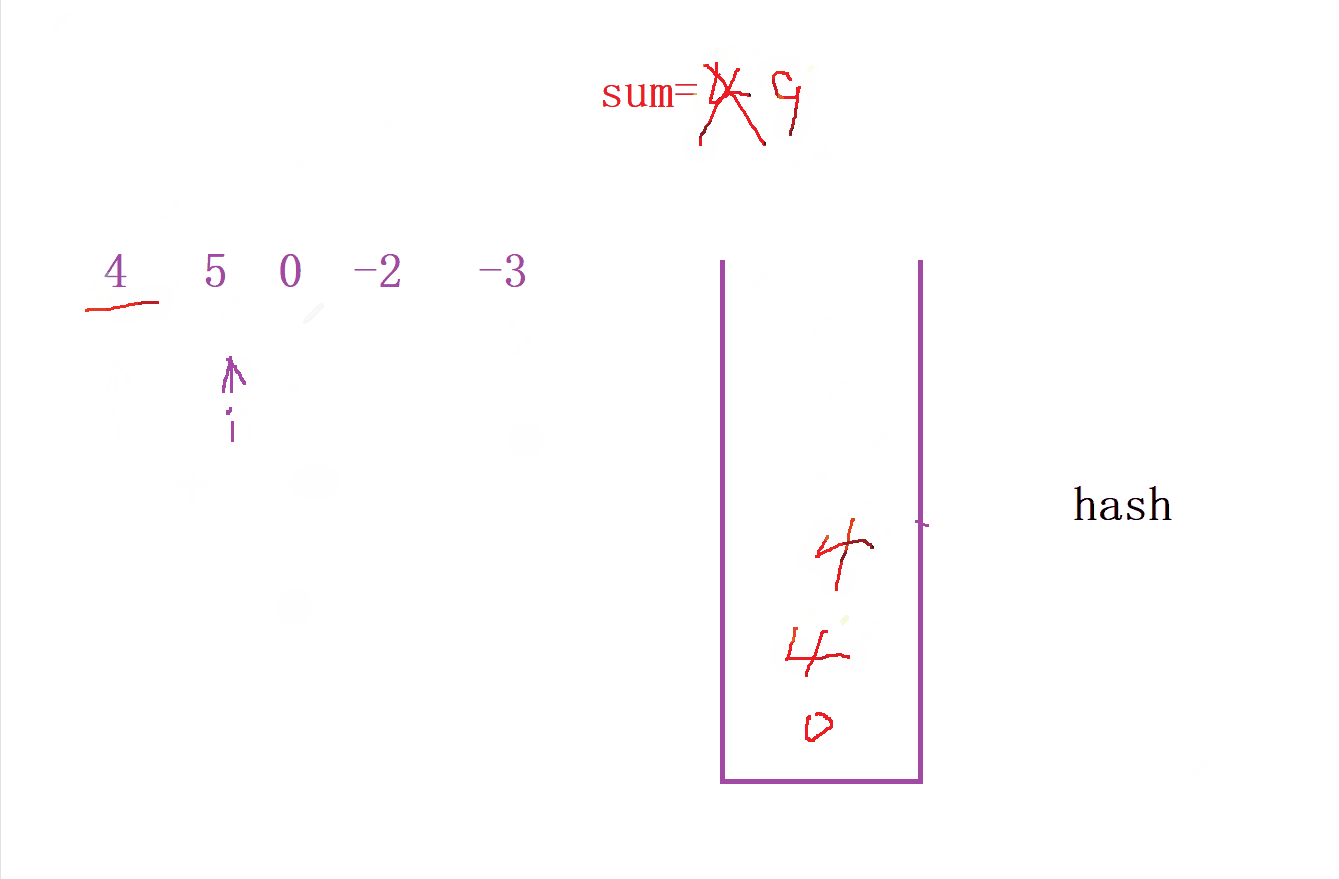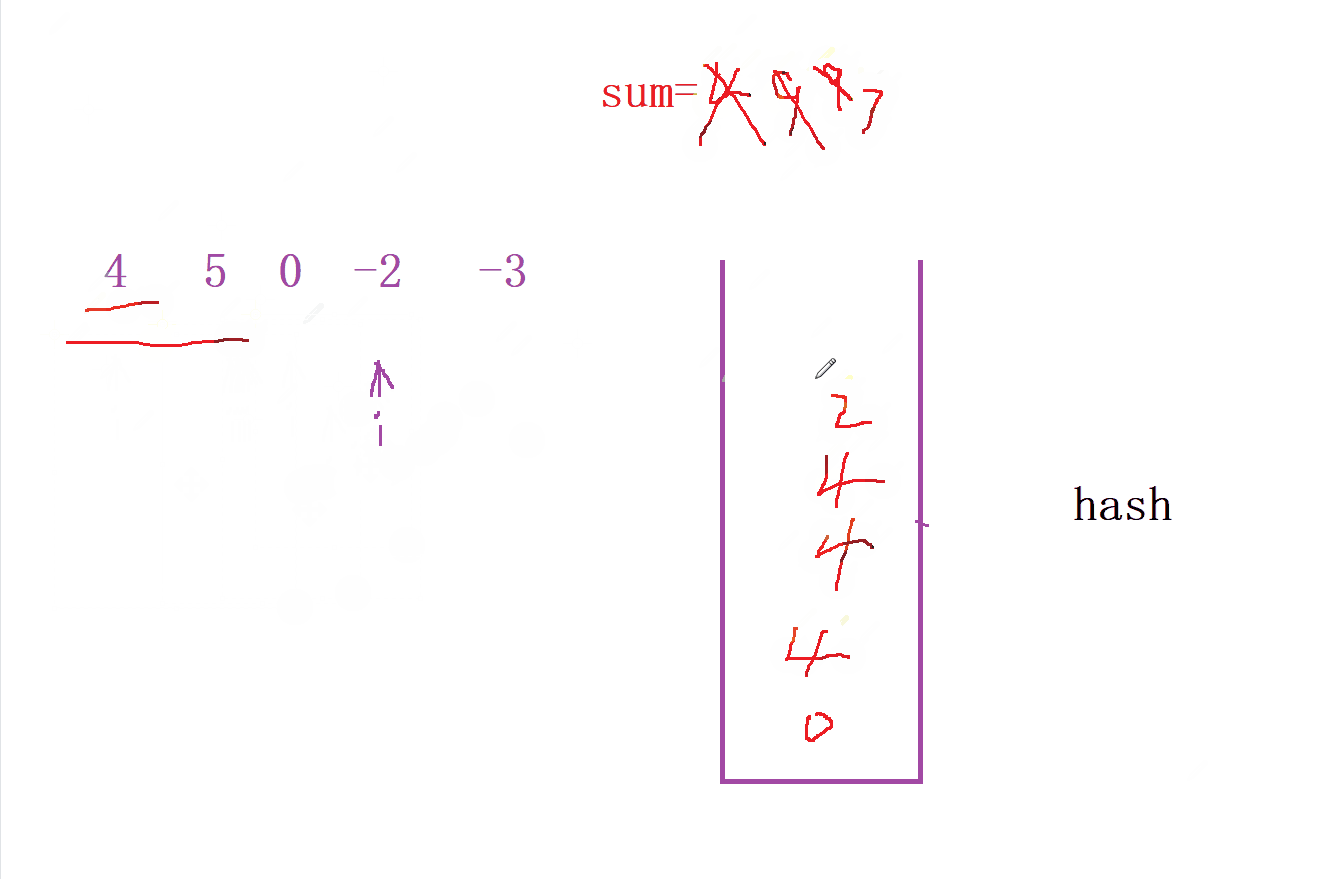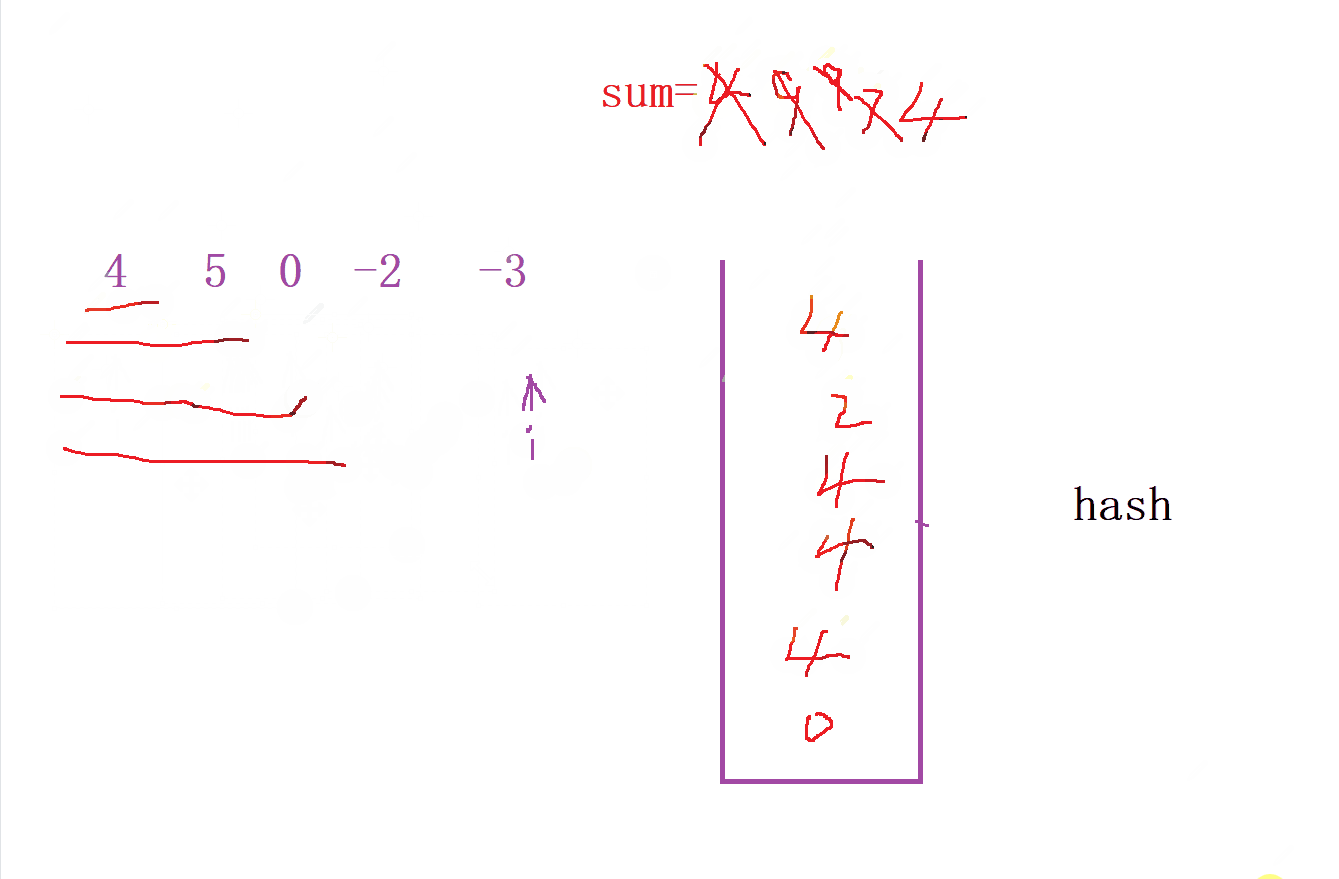
前綴和算法步驟

  • 設 i 為數組中的任意位置，用 sum[i] 表示 [0, i] 區間內所有元素的和。

  • 想知道有多少個「以 i 為結尾的可被 k 整除的子數組」，就要找到有多少個起始位置為 x1, x2 , x3 … 使得 [x, i] 區間內的所有元素的和可被 k 整除。

  • 設 [0, x - 1] 區間內所有元素之和等于 a ， [0, i] 區間內所有元素的和等于 b ，可得 (b - a) % k == 0 。

  • 由 同余定理 可得， [0, x - 1] 區間與 [0, i] 區間內的前綴和同余。于是問題就變成：

  • 找到在 [0, i - 1] 區間內，有多少前綴和的余數等于 sum [i] % k 的即可。

在這里插入圖片描述

  1. 我們先定義一個 哈希表 來統計每次 前綴和的個數 ， 并且尋找中間到是否 前綴和 中是否出現的 個數
  1. 然后我們就可以通過哈希表來尋找滿足 sum[i] % k 的 個數

請添加圖片描述

<3>. 編寫代碼


class Solution {public int subarraysDivByK(int[] nums, int k) {// 定義 一個哈希表Map<Integer, Integer> map= new HashMap<>();int n= nums.length;int ret=0,sum=0;// 可以理解為 從 0 位置放入 0 數據 map.put(0/k,1);for(int i=0; i < n; ++i ) {sum += nums[i];// 除去 Java 中 取模是 負數的情況int r=  (sum % k + k) % k  ;// 通過 余值定理 可知// sum % k =   a  % k// 這里就可以轉化成 前面 【0, i-1】的位置 // 是否存在 哈希表中ret += map.getOrDefault(r,0);// 將前綴和數據放入 哈希表中map.put(r,map.getOrDefault(r,0)+1);}return ret;}
}

在這里插入圖片描述

魚式瘋言

對于本題小編最大的體會

  1. 當我們需要求 某個數 的子數組 時， 借用 前綴和 和 哈希表 的結合來尋找 前面的出現的 前綴和 來 查找是否滿足 該數字 的方法
   // 可以理解為 從 0 位置放入 0 數據 map.put(0/k,1);
  1. 細節處理

如果整段數值 前綴和為0 ， 那么我們就需要制定一個 默認值 為 0 來進入哈希表

3. 連續數組

525.連續數組題目鏈接

<1>. 題目描述

在這里插入圖片描述

給定一個二進制數組 nums , 找到含有相同數量的 0 和 1 的 最長連續子數組，并返回該 子數組 的長度。

示例 1:

輸入: nums = [0,1]
輸出: 2
說明: [0, 1] 是具有相同數量 0 和 1 的最長連續子數組。

示例 2:

輸入: nums = [0,1,0]
輸出: 2
說明: [0, 1] (或 [1, 0]) 是具有相同數量0和1的最長連續子數組。

題目含義 :

尋找 一個 最長的連續子數組 0 和 1 個想等的 長度

<2>. 講解算法思想

題目分析

我們要 0 和 1 的個數想等， 那么我們確定 0 和 1 的個數想等呢 ？

我們可以思考一下， 如果 把 0 改成 -1 ， 只要 -1 和 1 相加 為 0 不就 個數相等 了嗎？ 🤔 🤔 🤔

算法步驟

從上一題的思路可得， 我們的目的就是要尋找 總和 為 0 的 一段子數組， 我們就可以借助 哈希表 和 前綴和 。

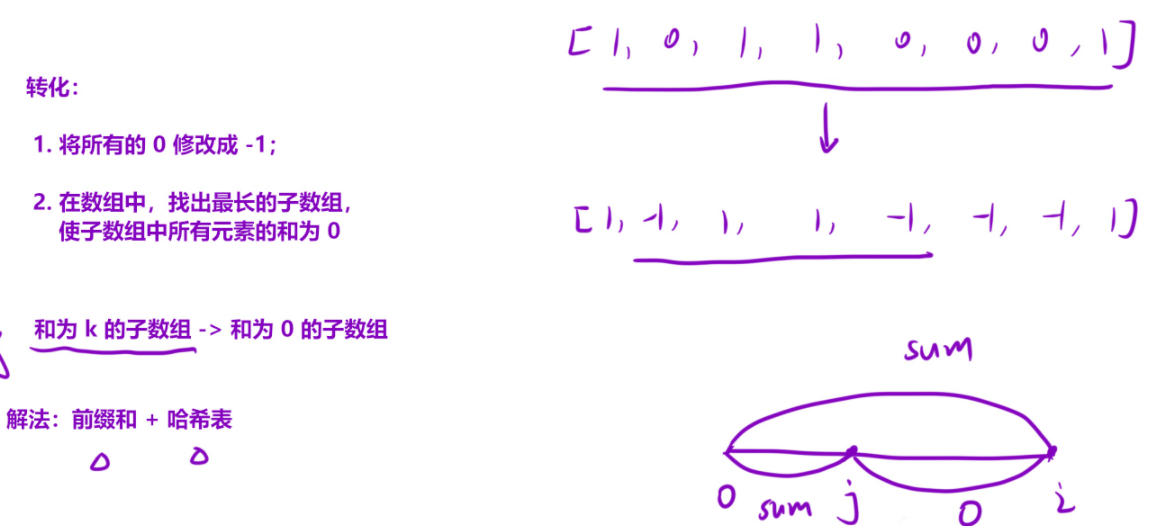
在這里插入圖片描述

那么我們本質上還是尋找 在現有的一段前綴和中去尋找一段區間是否 等于 0 的個數

我們先定義一個 哈希表， 因為我們要的長度， 但這個哈希表統計的是當前位置的下標。

在這里插入圖片描述

<3>. 編寫代碼

class Solution {public int findMaxLength(int[] nums) {int n= nums.length;// 定義個哈希表 // 左邊為前綴和 ， 右邊 為 下標位置Map<Integer , Integer> map= new HashMap<>();int len=0,sum = 0;map.put(0,-1);// 前綴和 + 哈希表for(int j=0; j < n ; j++) {// 進行前綴和   sum +=  (nums[j]==0 ? -1 : 1) ;// 這個本質上還是相當于 用 getOrdefault() 來判斷// 更新結果if(map.containsKey(sum)) {len=Math.max(len,j - map.get(sum) );} else {// 如果不存在該前綴和 就 進行哈希表// 這里的細節就是 // 不需要進入重復元素map.put(sum,j);}}return len;}
}

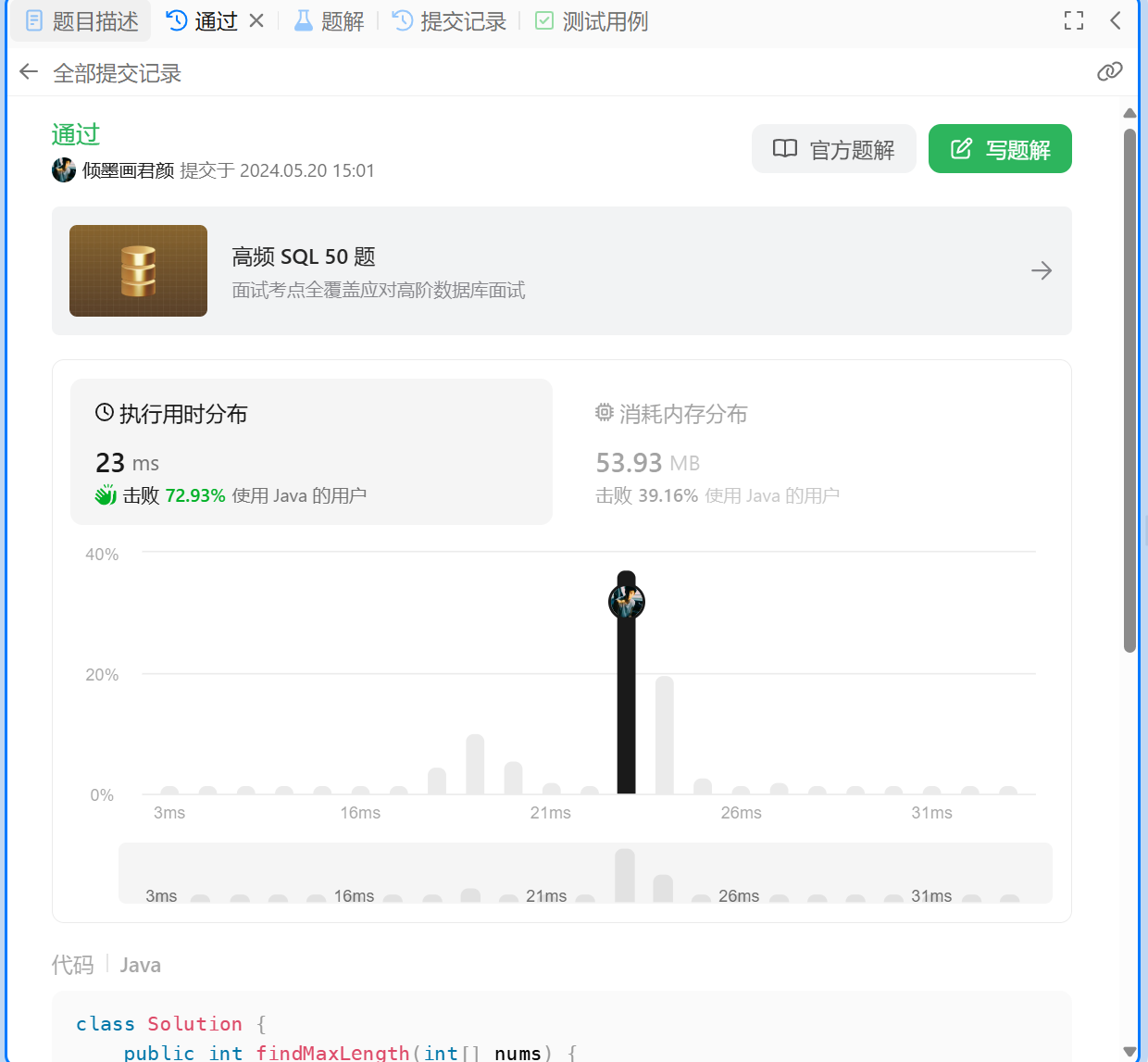
在這里插入圖片描述

魚式瘋言

對于本題小編最大的體會還是 0 轉 -1 從而 轉化 成 總數為 0 這個思路

但核心還是我們的 前綴和+哈希表 來尋找我們一段子數組 中和 為 某個數 的方法

細節處理 ：

細節一 ：

   map.put(0,-1);

定義一個 初始下標為 -1 ， 方便我們計算數組的 長度，并處理 邊界條件

// 更新結果if(map.containsKey(sum)) {len=Math.max(len,j - map.get(sum) );} else {// 如果不存在該前綴和 就 進行哈希表// 這里的細節就是 // 不需要進入重復元素map.put(sum,j);}

細節二 :

當該數字存在時，由于我們需要的數組的 最大長度， 當出現下一個同樣數字時， 左邊的下標 的值就會 增大，從而導致 j - 左邊下標值 減小

數組長度減少 。

4.二維數組的前綴和

dp35. 二維數組的前綴和題目鏈接

<1>. 題目描述

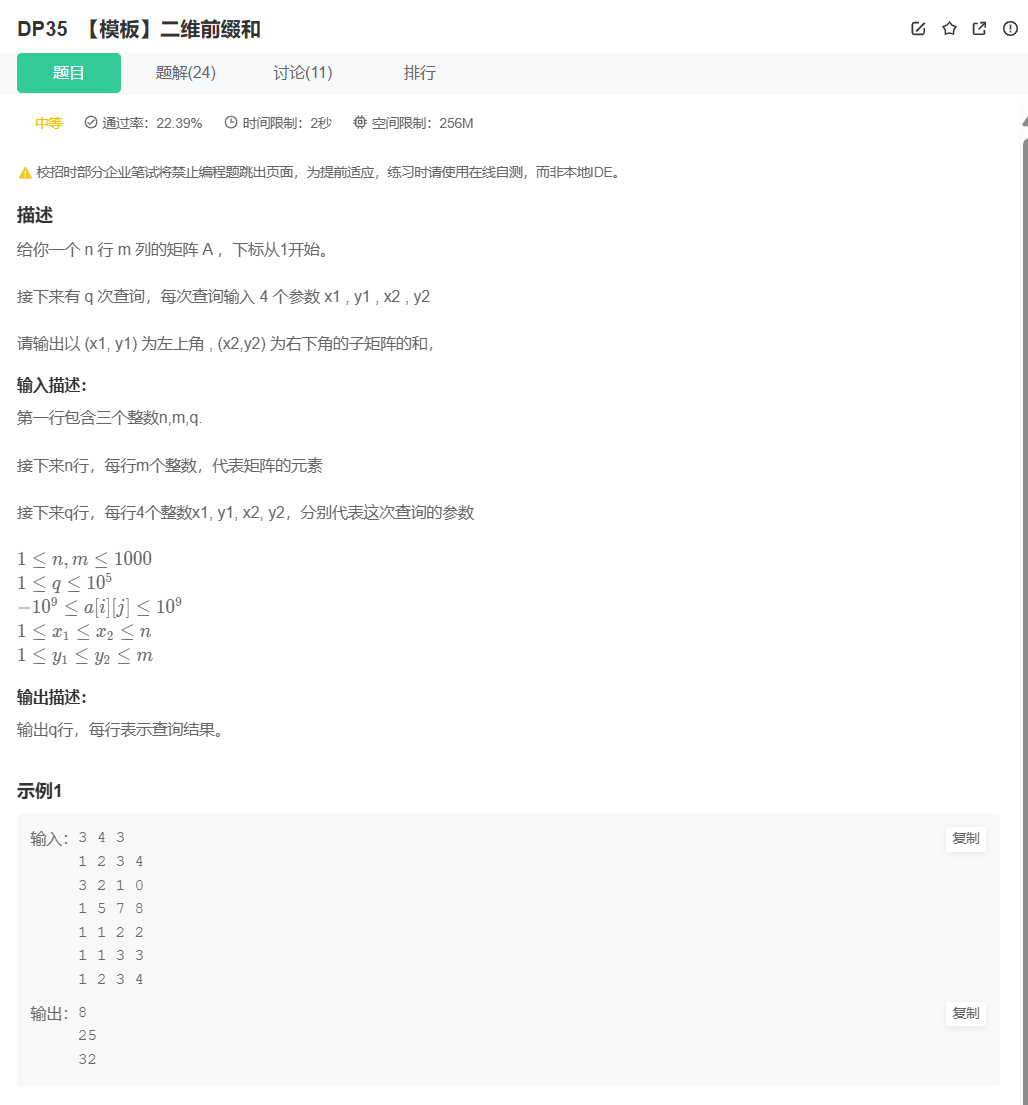
在這里插入圖片描述

題目含義 ：

給定一個 左上角 和 右下角的坐標，求出左下角和 右下角坐標所圍成的 矩陣的 數字總和

<2>. 講解算法思想

題目分析 ：

想要求本題，最好的思路還是利用我們的二維前綴和的思想

那么我們的 二維前綴和 該怎么計算 ？ ？ ？

提示一下 ：

我們需要在一維前綴和的基礎上進行把 二維數組進行拆分 即可

算法步驟:

類比于一維數組的形式，如果我們能處理出來從 == [0, 0]== 位置到 == [i, j] == 位置這片區域內所有
元素的累加和，就可以在 O(1) 的時間內，搞定矩陣內任意區域內所有元素的 累加和 。因此我們
接下來僅需完成兩步即可：

  • 第一步：搞出來 前綴和矩陣

這里就要用到 一維數組 里面的拓展知識，我們要在矩陣的最上面和最左邊添加上一行和一列 0，這樣我們就可以省去非常多的 邊界條件 的處理（同學們可以自行嘗試直接搞出來前綴和矩陣，邊界條件的處理會讓你崩潰的）。處理后的矩陣就像這樣：

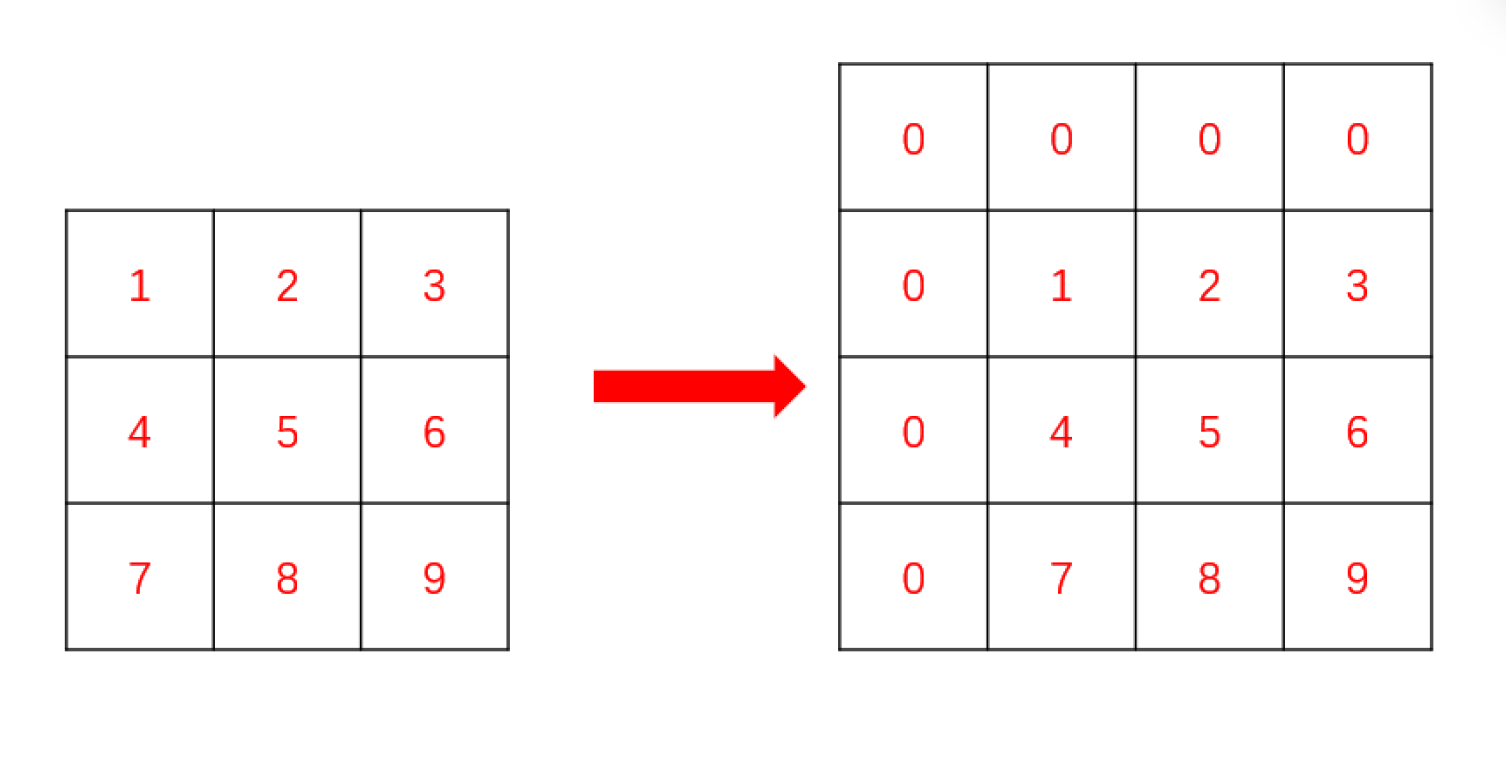
在這里插入圖片描述

  • 第二步

這樣，我們填寫前綴和矩陣數組的時候，下標直接從 1 開始，能大膽使用 i - 1 , j - 1 位
置的值。

注意 dp 表與原數組 matrix 內的元素的 映射關系：

i. 從 dp 表到 matrix 矩陣，橫縱坐標減一；

ii. 從 matrix 矩陣到 dp 表，橫縱坐標加一。

前綴和矩陣中 sum[i][j] 的含義，以及如何遞推二維前綴和方程

sum[i][j] 的含義：

sum[i][j] 表示，從 [0, 0] 位置到 [i, j] 位置這段區域內，所有元素的累加和。對應
下圖的紅色區域：

簡單來說就是：

如下圖，假設 紅色 區域為 a，紫色 區域為 b ， 綠色 區域為 d ， 橙色 區域為 c

計算前綴和時， 我們就可以把他們看成是一塊又一塊的區域來 累加

而我們通過這樣的分解區域是需要得到 a + b + c + d 總和的面積， 那我們就需要轉化成 s= (a+b) + (a+c) + d - a 從而得到我們 前綴和 數組

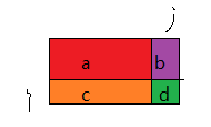
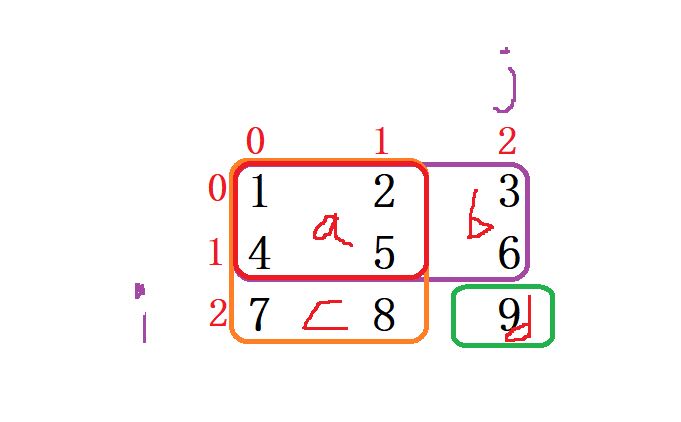
在這里插入圖片描述

在這里插入圖片描述

所以我們就可以推導出 dp[i][j] = dp[i][j-1] + dp[i-1][j] - dp[i-1][j-1] + nums[i][j];

那么我們該怎么使用 二維前綴和數組 呢 ？

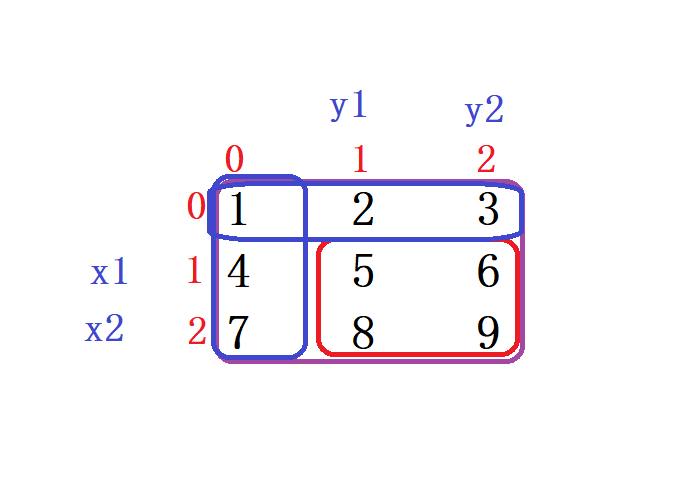
在這里插入圖片描述

我們想要得到紅色的區域，總得用 dp[x2][y2] - 區域 b - 區域 c + 區域 a 得到我們的區域 d

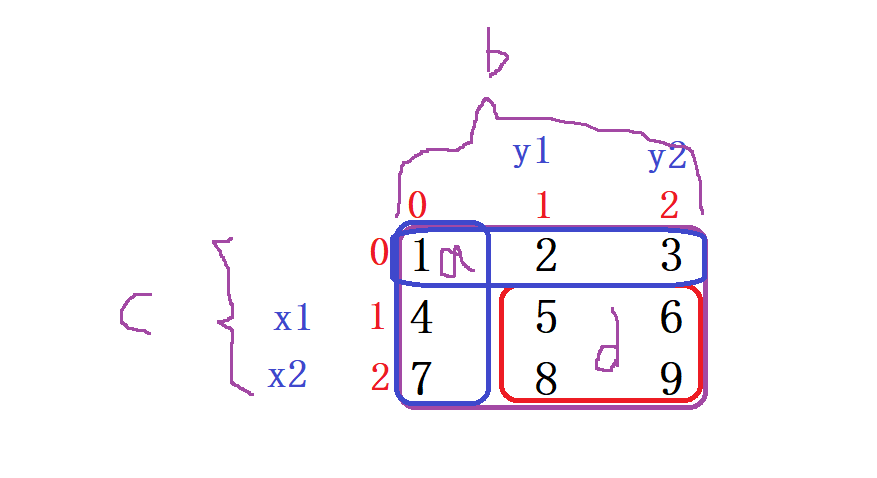
在這里插入圖片描述

從中我們可以推導出 使用二維前綴和的公式為 ： d = dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1];

<3>. 編寫代碼

import java.util.Scanner;// 注意類名必須為 Main, 不要有任何 package xxx 信息
public class Main {public static void main(String[] args) {Scanner in = new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的區別int n = in.nextInt(), m = in.nextInt(), q = in.nextInt();long array[][] = new long[n + 1][m + 1];for (int i = 1; i < n + 1; ++i) {for (int j = 1; j < m + 1; j++) {array[i][j] = in.nextInt();}}long dp[][] = new long[n + 1][m + 1];for (int i = 1; i < n + 1; ++i) {for (int j = 1; j < m + 1; j++) {dp[i][j] = dp[i][j - 1] + dp[i - 1][j] + array[i][j] - dp[i - 1][j - 1];}}while (q > 0) {int x1 = in.nextInt(), y1 = in.nextInt(), x2 = in.nextInt(), y2 = in.nextInt();long sum = dp[x2][y2] - dp[x2][y1 - 1] - dp[x1 - 1][y2] + dp[x1 - 1][y1 - 1];System.out.println(sum);q--;}}
}

在這里插入圖片描述

三.前綴和算法的總結

  • 我們先初步認識了前綴和算法本質上就是 0到i 位置的和的一個數組， 我們通過 基本前綴和數組 通過轉化進行來實現對 子數組 的計算 。

  • 更在 ‘除自身以外的乘積’的上， 我們認識到也可以同時構造 前綴和 以及 后綴和 的思想來實現對我數組 兩頭的同時計算

  • 以及在 ‘和可被 k 整除的子數組’ 和 ‘連續數組’ 中 ， 我們認識到 可以用 前綴和 搭配 哈希表 來 尋找某個固定值 的子數組的 個數 或者 下標

  • 最后的二維數組， 更讓我們在 矩陣區域的思維 上進行 把 二維數組 進行劃分成一段一段我們 已有的的區域 ， 來 初始化和使用 我們的 二維前綴和數組

如果覺得小編寫的還不錯的咱可支持 三連 下 (定有回訪哦) , 不妥當的咱請評論區 指正

希望我的文章能給各位寶子們帶來哪怕一點點的收獲就是 小編創作 的最大 動力 💖 💖 💖

在這里插入圖片描述

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/bicheng/15862.shtml
繁體地址，請注明出處：http://hk.pswp.cn/bicheng/15862.shtml
英文地址，請注明出處：http://en.pswp.cn/bicheng/15862.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

代碼審計--一道簡單的文件包含題目的多種利用方式

代碼審計--一道簡單的文件包含題目的多種利用方式

NO.1 傳統方法 首先來看下代碼 <?php error_reporting(0); if(isset($_GET["file"])){include($_GET["file"]); }else{highlight_file(__FILE__);phpinfo(); } ?>看完代碼后再來學習學習函數吧&#xff0c;畢竟菜啊&#xff01;&#xff01;&…
閱讀更多...
IronPython和C#交互

IronPython和C#交互

在C#環境中動態調用IronPython腳本&#xff0c;可以通過以下步驟實現&#xff1a; 安裝IronPython: 首先&#xff0c;確保你的項目中已經安裝了IronPython。可以通過NuGet包管理器來安裝IronPython。 創建IronPython運行環境: 在C#代碼中&#xff0c;你需要創建一個ScriptEngi…
閱讀更多...
NASA數據集——阿爾法噴氣式大氣實驗甲醛（HCHO）數據

NASA數據集——阿爾法噴氣式大氣實驗甲醛（HCHO）數據

Alpha Jet Atmospheric eXperiment Formaldehyde Data 簡介 阿爾法噴氣式大氣實驗甲醛數據 阿爾法噴氣式大氣實驗&#xff08;AJAX&#xff09;是美國國家航空航天局艾姆斯研究中心與 H211, L.L.C. 公司的合作項目&#xff0c;旨在促進對加利福尼亞、內華達和太平洋沿岸地區的…
閱讀更多...
【NOIP2014普及組復賽】題4：子矩陣

【NOIP2014普及組復賽】題4：子矩陣

題3&#xff1a;子矩陣 【題目描述】 給出如下定義&#xff1a; 1.子矩陣&#xff1a;從一個矩陣當中選取某些行和某些列交叉位置所組成的新矩陣&#xff08;保持行與列的相對順序&#xff09;被稱為原矩陣的一個子矩陣。 例如&#xff0c;下面左圖中選取第 2 、 4 2、4 2、…
閱讀更多...
vue項目中使用json編輯器

vue項目中使用json編輯器

實現效果&#xff1a; 借助插件json-editor-vue3實現效果如圖一&#xff0c;如果嫌丑可以通過類名改一下樣式如圖二。 實現過程&#xff1a; 安裝插件&#xff1a;npm install json-editor-vue3 文檔鏈接&#xff1a;GitCode - 開發者的代碼家園 <script setup name&quo…
閱讀更多...
Golang發送POST請求并傳遞JSON數據

Golang發送POST請求并傳遞JSON數據

客戶端 package mainimport ("c02_get_param/common""fmt""zdpgo_resty" )func main() {// Create a Resty Clientclient : zdpgo_resty.New()// 設置字符串resp, err : client.R().SetHeader("Content-Type", "application/jso…
閱讀更多...
AcWing 3466. 清點代碼庫(STL：map,vector)

AcWing 3466. 清點代碼庫(STL：map,vector)

3466. 清點代碼庫 需要求有幾種不同數列&#xff0c;每種有多少個&#xff0c;可以想到用map。它的鍵是一個數列&#xff0c;可以把它放在vector里。也就是map<vector<int>,int> 要滿足要求的輸出序列&#xff0c;就要想把它放在其他容器&#xff0c;或數組里&…
閱讀更多...
mac清理緩存的命令

mac清理緩存的命令

mac清理緩存的命令 在macOS中&#xff0c;你可以使用以下命令來清理緩存&#xff1a; 清理DNS緩存&#xff1a; sudo killall -HUP mDNSResponder 清理Metal緩存&#xff1a; mkdir ~/Library/Caches/com.apple.Metal 清理文件系統元數據緩存&#xff1a; sudo find /private/…
閱讀更多...
Vite + Vue3 部署 GitHub

Vite + Vue3 部署 GitHub

因為靜態資源是可以部署到 GitHub 上&#xff0c;自己順便學習部署網站 因為我使用的是 Vite 工具&#xff0c;官方有提供相應 Demo 部署靜態站點 | Vite 官方中文文檔 新建文件夾 .github 然后再建一個文件夾 workflows 新建文件 main.yml 文件 直接使用官方文檔 demo #…
閱讀更多...
什么是spring 的組件掃描？

什么是spring 的組件掃描？

Spring的組件掃描&#xff08;Component Scanning&#xff09;是Spring框架提供的一種機制&#xff0c;用于自動尋找和注冊應用程序中的組件&#xff0c;進而減少顯式的配置。這些組件通常是標有特定注解&#xff08;如Component, Service, Repository, Controller等&#xff0…
閱讀更多...
如何處理時間序列的缺失數據

如何處理時間序列的缺失數據

您是否應該刪除、插入或估算&#xff1f; 世界上沒有完美的數據集。每個數據科學家在數據探索過程中都會有這樣的感覺&#xff1a; df.info()看到類似這樣的內容&#xff1a; 大多數 ML 模型無法處理 NaN 或空值&#xff0c;因此如果您的特征或目標包含這些值&#xff0c;則在…
閱讀更多...
Java-MySql：JDBC

Java-MySql：JDBC

目錄 JDBC概述 JDBC搭建 1、導入mysql開發商提供的jar包 2、注冊驅動 3、與數據庫連接 注解&#xff1a; Statement&#xff1a; 代碼 運行 PreparedStatement&#xff1a; 代碼 運行 PreparedStatement和Statement Statement 增 代碼 運行 刪 代碼 運…
閱讀更多...
九、圖形化腳本

九、圖形化腳本

多年來&#xff0c; shell腳本一直都被認為是枯燥乏味的。但如果你準備在圖形化環境中運行腳本時&#xff0c;就未必如此了。有很多與腳本用戶交互的方式并不依賴read和echo語句。 9.1 創建文本菜單 創建交互式shell腳本最常用的方法是使用菜單。提供各種選項可以幫助腳本用戶…
閱讀更多...
AI遇上遙感，未來會怎樣？

AI遇上遙感，未來會怎樣？

隨著航空、航天、近地空間等多個遙感平臺的不斷發展&#xff0c;近年來遙感技術突飛猛進。由此&#xff0c;遙感數據的空間、時間、光譜分辨率不斷提高&#xff0c;數據量也大幅增長&#xff0c;使其越來越具有大數據特征。對于相關研究而言&#xff0c;遙感大數據的出現為其提…
閱讀更多...
初識GPT

初識GPT

初識GPT GPT&#xff08;Generative Pre-trained Transformer&#xff09;是一種基于Transformer架構的預訓練語言模型&#xff0c;由人工智能研究公司OpenAI開發。GPT模型使用了一種稱為“自回歸”&#xff08;autoregressive&#xff09;的方法來生成文本&#xff0c;這意味…
閱讀更多...
Oracle執行DELETE語句后，回滾(還原)數據

Oracle執行DELETE語句后，回滾(還原)數據

--第一步&#xff1a;刪除數據 DELETE FROM "EMPLOYEER" WHERE id 123 --第二步&#xff1a;查看數據列表(判斷第一步中數據是否被刪除) SELECT * FROM "EMPLOYEER" AS OF timestamp to_timestamp( 2024-05-22 11:51:00, yyyy-mm-dd hh24:mi:ss ) --第…
閱讀更多...
基于MetaGPT構建LLM多智能體

基于MetaGPT構建LLM多智能體

前言 你好&#xff0c;我是GISer Liu&#xff0c;在上一篇文章中&#xff0c;我們用了兩萬多字詳細拆解了單個Agent的組成&#xff0c;并通過Github Trending訂閱智能體理解MetaGPT框架的訂閱模塊如何解決應用問題&#xff0c;但是對于復雜&#xff0c;并行的任務&#xff0c;單…
閱讀更多...
【vue】el-select選擇器實現寬度自適應

【vue】el-select選擇器實現寬度自適應

選擇器的寬度根據內容長度進行變化 <div class"Space_content"><el-selectv-model"value":placeholder"$t(bot.roommessage)"class"select"size"small"style"margin-right: 10px"change"selectcha…
閱讀更多...
JavaSE——集合框架二（1/6）-前置知識-可變參數、Collections工具類

JavaSE——集合框架二（1/6）-前置知識-可變參數、Collections工具類

目錄 可變參數 Collections工具類 Collections的常用靜態方法 實例演示 可變參數 可變參數 就是一種特殊形參&#xff0c;定義在方法、構造器的形參列表里&#xff0c;格式是&#xff1a;數據類型...參數名稱 可變參數的特點和好處 特點&#xff1a;可以不傳數據給它&am…
閱讀更多...
SQL常用基礎語句（一）-- ABCDE開頭

SQL常用基礎語句（一）-- ABCDE開頭

AS 將列名從 count(*) 修改為 total select count(*) as total from users where status0 將列名 username 改為 uname&#xff0c; password 改為 upwd select username as uname, password as upwd from users BETWEEN AND 說明&#xff1a;BETWEEN 篩選的是 >value1且 &l…
閱讀更多...
最新文章

Copyright @ 2022~2023