簡介：遞歸、搜索與回溯，本節博客主要是簡單記錄一下關于“遞歸、搜索與回溯”的相關簡單概念，為后續算法做鋪墊。

遞歸、搜索、回溯的關系：

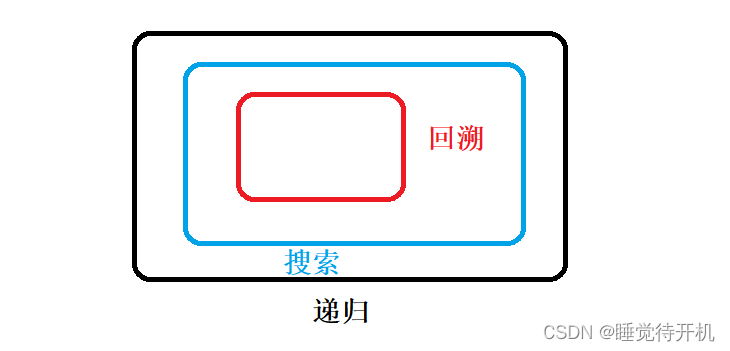
1.遞歸

1.1遞歸概念

函數自己調用自己

2.2遞歸意義

遞歸具有多種意義，比如二叉樹的遍歷、快排、歸并…

本質：用于解決主問題的方法f，在子問題中也可以適用，即有限“套娃”

2.3學習遞歸

• 遞歸展開圖
• 多練習題目
• 宏觀看待遞歸過程
  • 不要在意遞歸細節展開
  • 將遞歸函數看成一個黑盒
  • 認為黑盒可以解決此問題

2.4寫遞歸代碼步驟

遞歸代碼往往比較簡短，但是要注意思考的步驟：

• 1.函數頭的設計：找相同的子問題，根據需要設計參數
• 2.函數體的編寫：只關心一個子問題的解決方案
• 3.函數結束：注意遞歸結束條件

2.搜索

搜索 分為深度 優先搜索(dfs) 和 廣度搜索(bfs) ，仍屬于暴力遍歷。

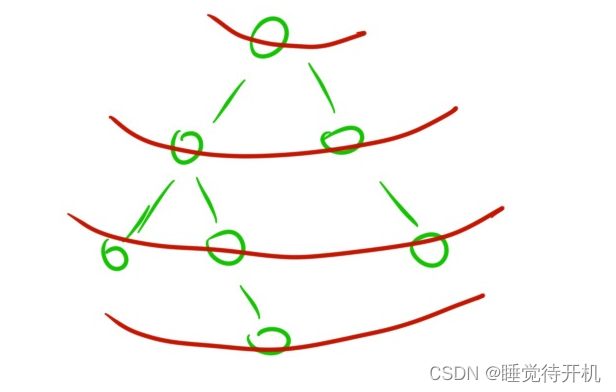
以二叉樹為例，來解釋dfs與bfs：
dfs：

bfs：

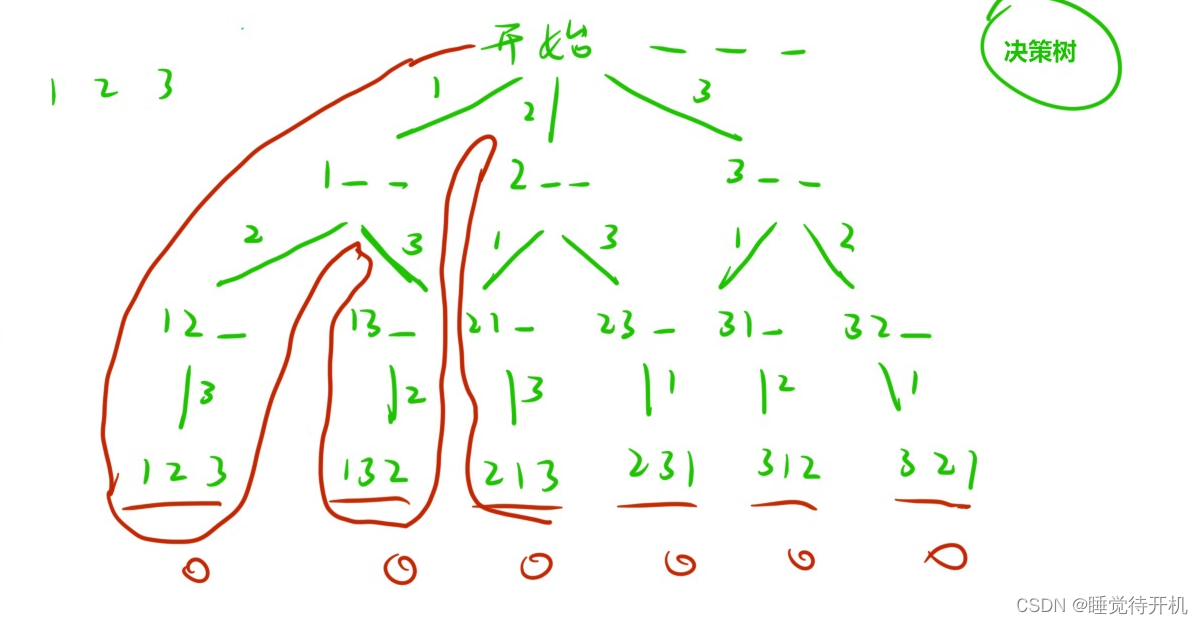
拓展：全排列問題也可以用深度優先遍歷來進行解決。
例如：

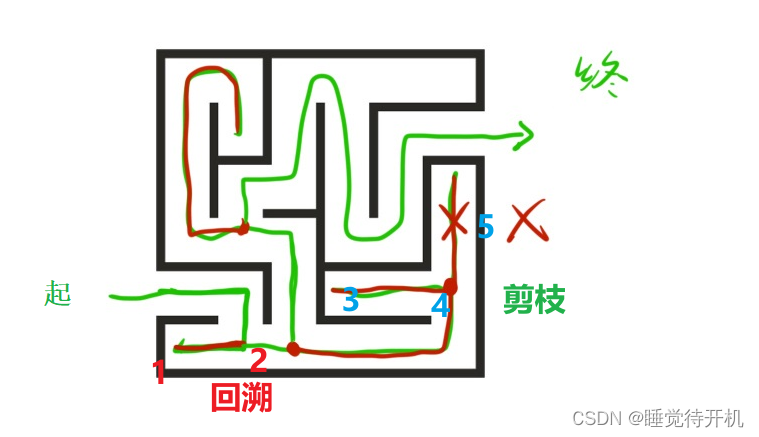
3.回溯與剪枝

回溯：嘗試某種情況發現走不通所進行的回到最近分界點的過程。

剪紙：當通過會u是回到分界點時，已經確定某一條魯不具有可行性，從而排除這種選擇稱之為剪枝。

---

EOF