大家好,蒙特卡洛模擬是一種廣泛應用于各個領域的計算技術,它通過從概率分布中隨機抽取大量樣本,并對結果進行統計分析,從而模擬復雜系統的行為。這種技術具有很強的適用性,在金融建模、工程設計、物理模擬、運籌優化以及風險管理等領域都有廣泛的應用。
蒙特卡洛模擬這個名稱源自于摩納哥王國的蒙特卡洛城市,這里曾經是世界著名的賭博天堂。在20世紀40年代,著名科學家烏拉姆和馮·諾依曼參與了曼哈頓計劃,他們需要解決與核反應堆中子行為相關的復雜數學問題。他們受到了賭場中擲骰子的啟發,設想用隨機數來模擬中子在反應堆中的擴散過程,并將這種基于隨機抽樣的計算方法命名為"蒙特卡洛模擬"(Monte Carlo simulation)。
蒙特卡洛模擬的核心思想是通過大量重復隨機試驗,從而近似求解分析解難以獲得的復雜問題。它克服了傳統數值計算方法的局限性,能夠處理非線性、高維、隨機等復雜情況。隨著計算機性能的飛速發展,蒙特卡洛模擬的應用范圍也在不斷擴展。
在金融領域,蒙特卡洛模擬被廣泛用于定價衍生品、管理投資組合風險、預測市場波動等。在工程設計中,它可以模擬材料力學性能、流體動力學等復雜物理過程。在物理學研究中,從粒子物理到天體物理,都可以借助蒙特卡洛模擬進行探索。此外,蒙特卡洛模擬還在機器學習、計算生物學、運籌優化等領域發揮著重要作用。
蒙特卡洛模擬的過程基本上是這樣的:首先需要定義要模擬的系統或過程,包括方程和參數;其次根據擬合的概率分布生成隨機樣本;進而針對每一組隨機樣本,運行模型模擬系統的行為;最后分析結果以了解系統行為。
本文將介紹使用它來模擬未來證券價格的兩種分布:高斯分布和學生 t 分布。這兩種分布通常被量化分析人員用于證券市場數據。
在此加載蘋果公司從2020年到2024年每日證券價格的數據:
import?yfinance?as?yf
orig?=?yf.download(["AAPL"],?start="2020-01-01",?end="2024-12-31")
orig?=?orig[('Adj?Close')]
orig.tail()
[*********************100%%**********************] 1 of 1 completed
Date
2024-03-08 170.729996
2024-03-11 172.750000
2024-03-12 173.229996
2024-03-13 171.130005
2024-03-14 173.000000
Name: Adj Close, dtype: float64
可以通過價格序列來計算簡單的日收益率,并將其呈現為柱狀圖。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
returns = orig.pct_change()
last_price = orig[-1]
returns.hist(bins=100)
?蘋果證券日收益柱狀圖
1.標準正態分布擬合收益率
證券的歷史波動率通常是通過計算每日收益率的標準差來進行,假設未來的波動率與歷史波動率相似。而直方圖則呈現了以0.0為中心的正態分布的形狀。為簡單起見,將該分布假定為均值為0,標準差為0的高斯分布。接下來計算出標準差(也稱為日波動率),預計明天的日收益率將會是高斯分布中的一個隨機值。
daily_volatility?=?returns.std()
rtn?=?np.random.normal(0,?daily_volatility)
第二天的價格是今天的價格乘以 (1+return %):
price?=?last_price?*?(1??+?rtn)
以上是證券價格和收益的基本財務公式。使用蒙特卡洛模擬預測明天的價格,可以隨機抽取另一個收益率,從而推算后天的價格,可以得出未來 200 天可能的價格走勢之一。當然,這只是一種可能的價格路徑。重復這個過程得出另一條價格路徑,重復過程 1,000 次,得出 1,000 條價格路徑。
import?warnings
warnings.simplefilter(action='ignore',?category=pd.errors.PerformanceWarning)num_simulations?=?1000
num_days?=?200
simulation_df?=?pd.DataFrame()
for?x?in?range(num_simulations):count?=?0????#?The?first?price?pointprice_series?=?[]rtn?=?np.random.normal(0,?daily_volatility)price?=?last_price?*?(1??+?rtn)price_series.append(price)#?Create?each?price?pathfor?g?in?range(num_days):rtn?=?np.random.normal(0,?daily_volatility)price?=?price_series[g]?*?(1??+?rtn)price_series.append(price)#?Save?all?the?possible?price?pathssimulation_df[x]?=?price_series
fig?=?plt.figure()
plt.plot(simulation_df)
plt.xlabel('Number?of?days')
plt.ylabel('Possible?prices')
plt.axhline(y?=?last_price,?color?=?'b',?linestyle?=?'-')
plt.show()
分析結果如下:價格起始于179.66美元,大部分價格路徑相互交疊,模擬價格范圍為100美元至500美元。
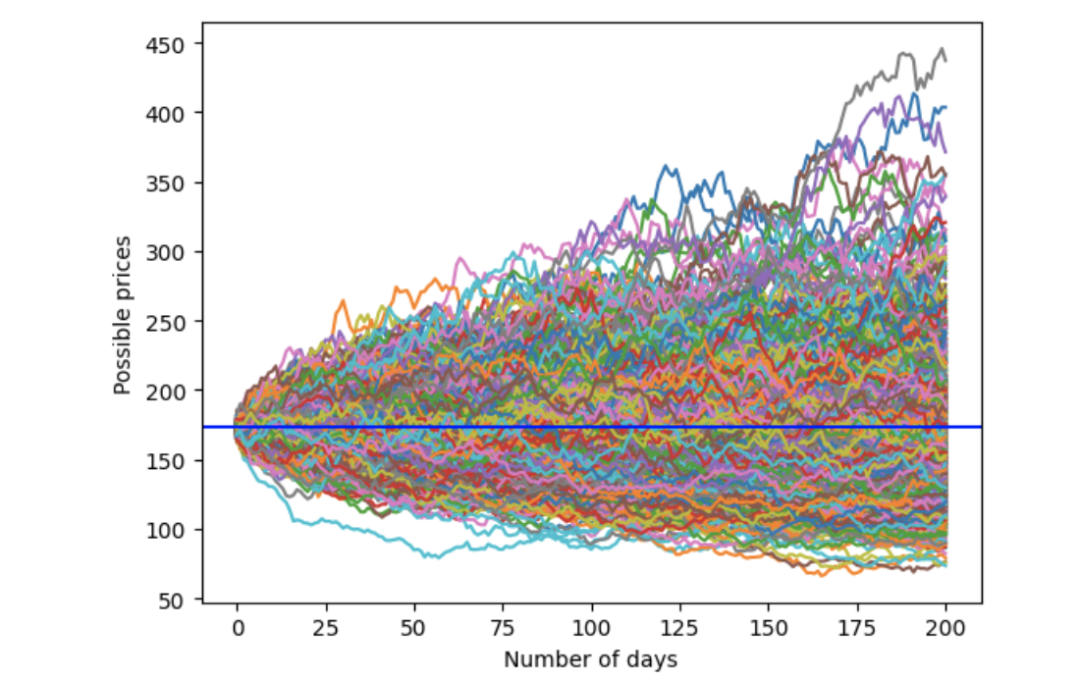
使用高斯分布的蒙特卡洛模擬
假設我們想知道90%情況下(5%到95%)出現的"正常"價格范圍,可以使用量化方法得到上限和下限,從而評估超出這些極端價格。
upper?=?simulation_df.quantile(.95,?axis=1)
lower?=?simulation_df.quantile(.05,?axis=1)
stock_range?=?pd.concat([upper,?lower],?axis=1)fig?=?plt.figure()
plt.plot(stock_range)
plt.xlabel('Number?of?days')
plt.ylabel('Possible?prices')
plt.axhline(y?=?last_price,?color?=?'b',?linestyle?=?'-')
plt.show()
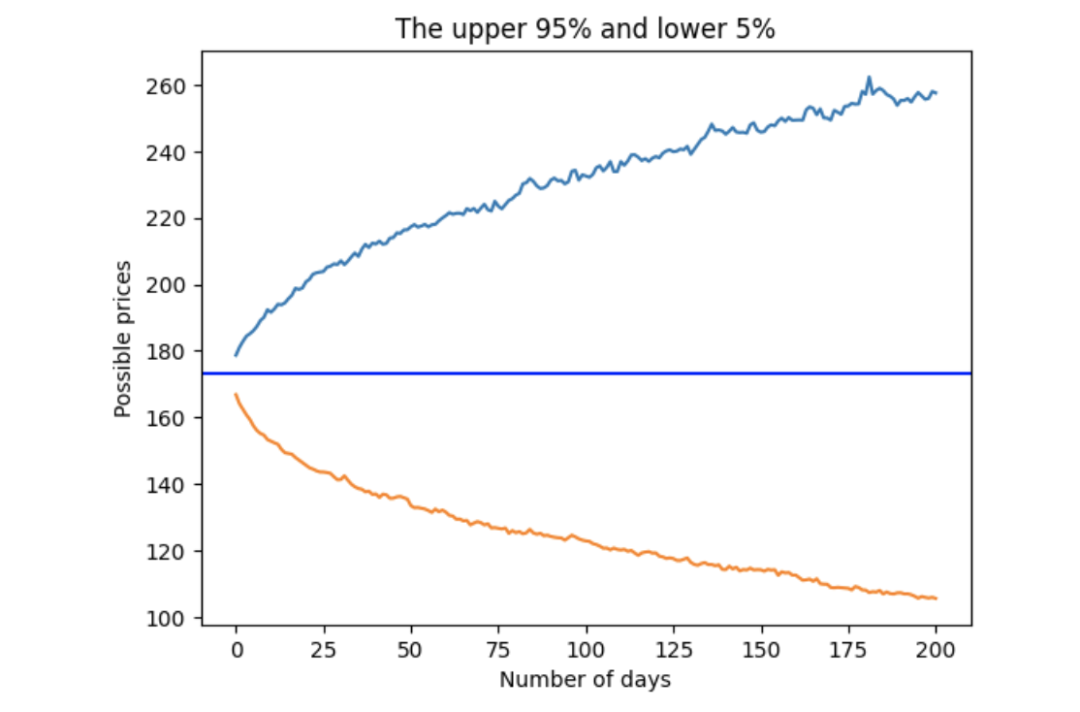
使用高斯分布的 95 百分位數和 5 百分位數
2.學生t分布擬合收益率
證券價格回報偶爾會出現極端事件,位于分布兩端。標準正態分布預計 95% 的收益率發生在兩個標準差之內,5% 的收益率發生在兩個標準差之外。如果極端事件發生的頻率超過 5%,分布看起來就會 "變胖"。這就是統計學家所說的肥尾,定量分析人員通常使用學生 t 分布來模擬證券收益率。
學生 t 分布有三個參數:自由度參數、標度和位置。
-
自由度:自由度參數表示用于估計群體參數的樣本中獨立觀測值的數量。自由度越大,t 分布的形狀越接近標準正態分布。在 t 分布中,自由度范圍是大于 0 的任何正實數。
-
標度:標度參數代表分布的擴散性或變異性,通常是采樣群體的標準差。
-
位置:位置參數表示分布的位置或中心,即采樣群體的平均值。當自由度較小時,t 分布的尾部較重,類似于胖尾分布。
用學生 t 分布來擬合實際證券收益率:
import?numpy?as?np
import?matplotlib.pyplot?as?plt
from?scipy.stats?import?treturns?=?orig.pct_change()#?Number?of?samples?per?simulation
num_samples?=?100#?distribution?fitting
returns?=?returns[1::]?#?Drop?the?first?element,?which?is?"NA"
params?=?t.fit(returns[1::])?#?fit?with?a?student-t#?Generate?random?numbers?from?Student's?t-distribution
results?=?t.rvs(df=params[0],?loc=params[1],?scale=params[2],?size=1000)
#?Generate?random?numbers?from?Student's?t-distribution
results?=?t.rvs(df=params[0],?loc=params[1],?scale=params[2],?size=1000)
print('degree?of?freedom?=?',?params[0])
print('loc?=?',?params[1])
print('scale?=?',?params[2])
參數如下:
-
自由度 = 3.735
-
位置 = 0.001
-
標度 = 0.014
使用這些參數來預測 Student-t 分布,然后用 Student-t 分布繪制實際證券收益分布圖。
returns.hist(bins=100,density=True,?alpha=0.6,?color='b',?label='Actual?returns?distribution')#?Plot?histogram?of?results
plt.hist(results,?bins=100,?density=True,?alpha=0.6,?color='g',?label='Simulated?Student/t?distribution')plt.xlabel('Value')
plt.ylabel('Density')
plt.title('Actual?returns?vs.?Projections?with?a?Student\'s?t-distribution')
plt.legend(loc='center?left')
plt.grid(True)
plt.show()
實際回報與預測相當接近:
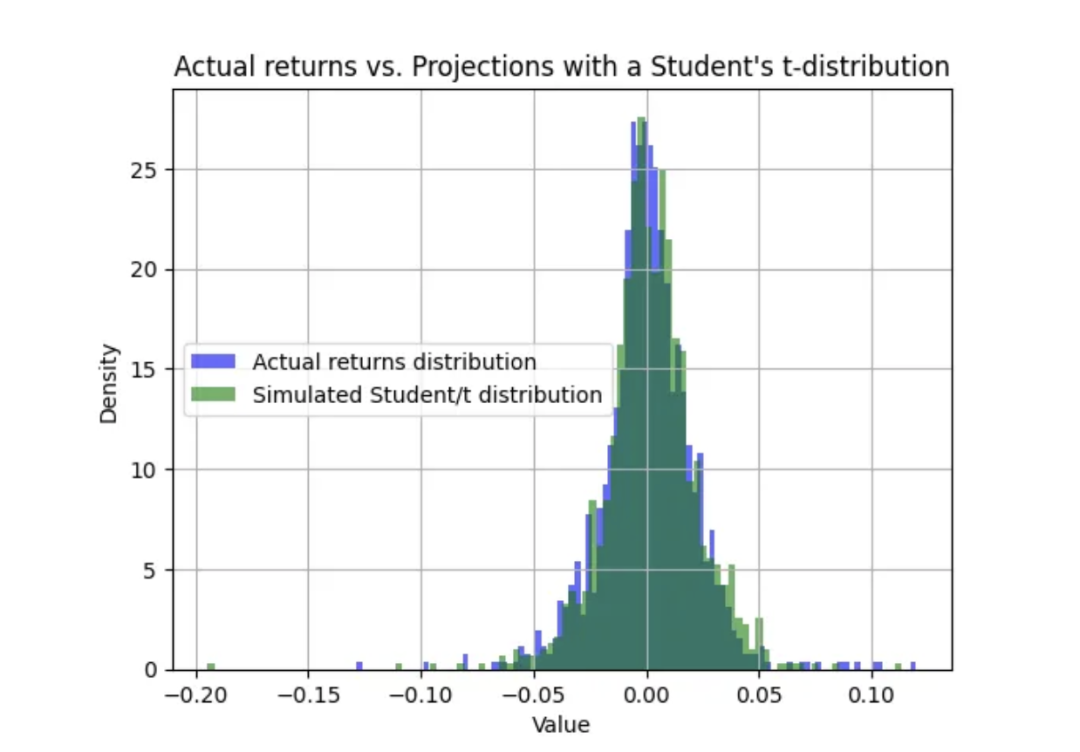
實際收益與學生 t 分布預測對比
與之前一樣,模擬未來 200 天的價格走勢。
import?warnings
warnings.simplefilter(action='ignore',?category=pd.errors.PerformanceWarning)num_simulations?=?1000
num_days?=?200
simulation_student_t?=?pd.DataFrame()
for?x?in?range(num_simulations):count?=?0#?The?first?price?pointprice_series?=?[]rtn?=?t.rvs(df=params[0],?loc=params[1],?scale=params[2],?size=1)[0]price?=?last_price?*?(1??+?rtn)price_series.append(price)#?Create?each?price?pathfor?g?in?range(num_days):rtn?=?t.rvs(df=params[0],?loc=params[1],?scale=params[2],?size=1)[0]price?=?price_series[g]?*?(1??+?rtn)price_series.append(price)#?Save?all?the?possible?price?pathssimulation_student_t[x]?=?price_series
fig?=?plt.figure()
plt.plot(simulation_student_t)
plt.xlabel('Number?of?days')
plt.ylabel('Possible?prices')
plt.axhline(y?=?last_price,?color?=?'b',?linestyle?=?'-')
plt.show()
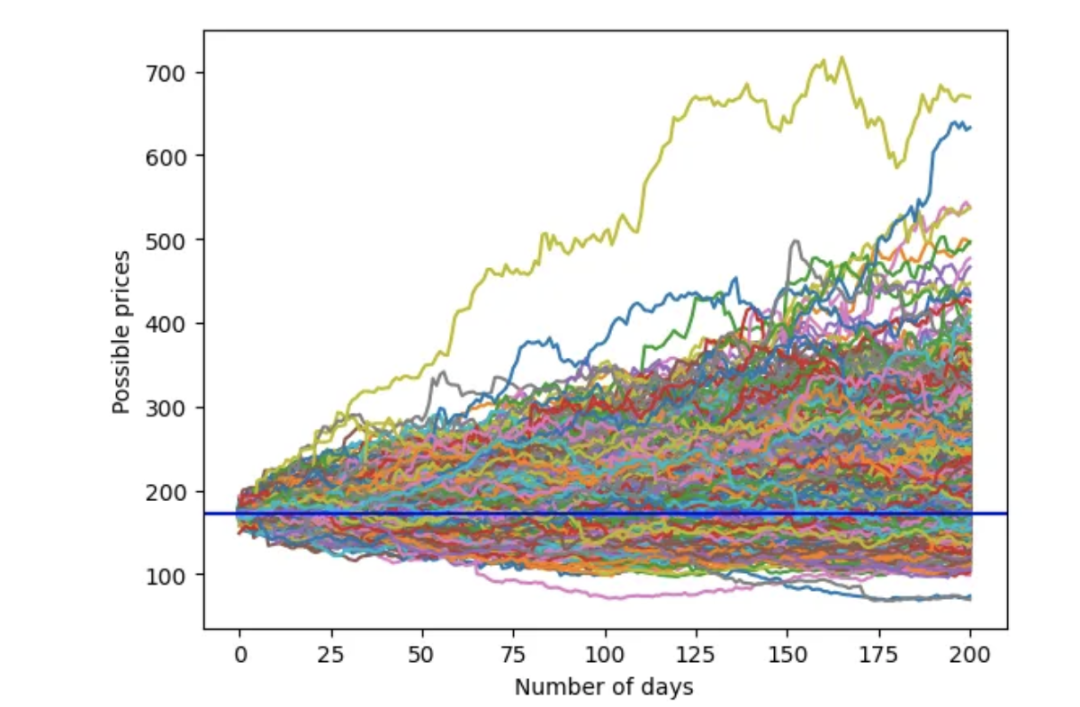
學生 t 分布的蒙特卡洛模擬
可以繪制出學生 t 的蒙特卡洛模擬置信區間上下限(95%、5%):
upper?=?simulation_student_t.quantile(.95,?axis=1)
lower?=?simulation_student_t.quantile(.05,?axis=1)
stock_range?=?pd.concat([upper,?lower],?axis=1)fig?=?plt.figure()
plt.plot(stock_range)
plt.xlabel('Number?of?days')
plt.ylabel('Possible?prices')
plt.title('The?upper?95%?and?lower?5%')
plt.axhline(y?=?last_price,?color?=?'b',?linestyle?=?'-')
plt.show()
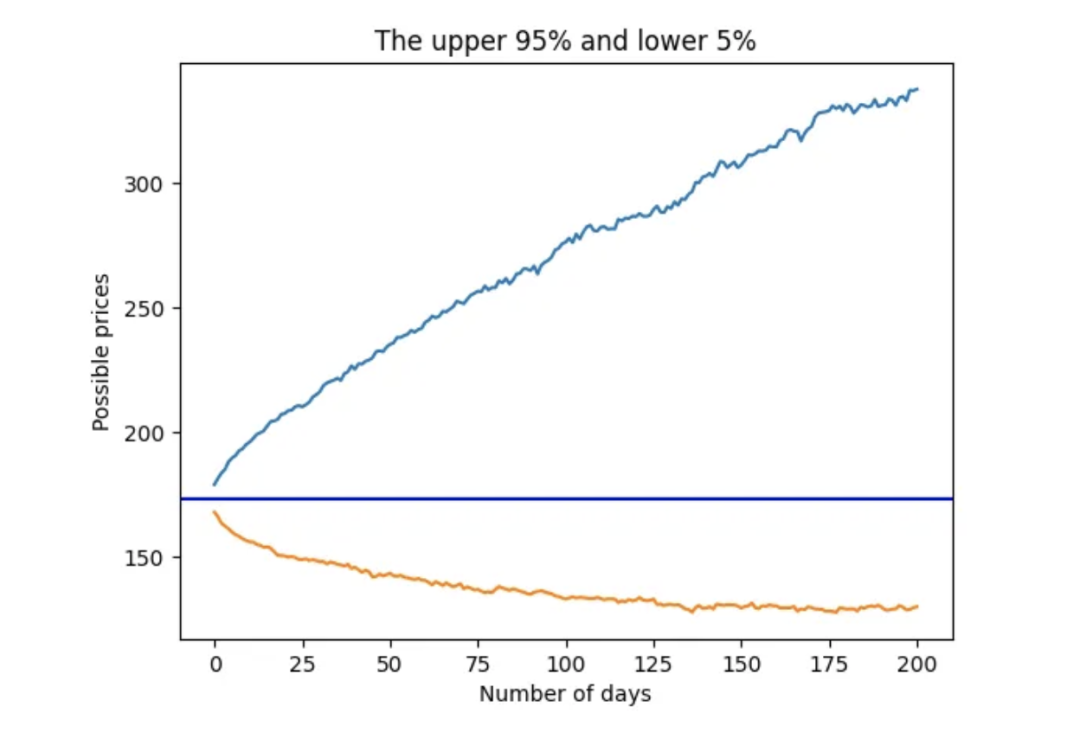
使用學生 t 分布的 95 百分位數和 5 百分位數
【獨一無二】)




)









,函數指針)
與解決策略)


