從反向傳播（BP）到BPTT：詳細數學推導【原理理解】

從反向傳播到BPTT：詳細推導與問題解析

在本文中，我們將從反向傳播算法開始，詳細推導出反向傳播通過時間（Backpropagation Through Time, BPTT）算法。重點討論BPTT中的梯度消失和梯度爆炸問題，并解釋如何解決這些問題。假設讀者已經具備反向傳播的基本知識，我們將簡要回顧反向傳播的核心概念，然后深入解析BPTT算法。

反向傳播算法的簡要回顧

反向傳播算法（Backpropagation）是用于訓練神經網絡的一種有效方法。其核心思想是通過鏈式法則（Chain Rule）計算損失函數相對于各個權重的梯度，然后使用梯度下降法更新權重。以下是反向傳播的主要步驟：

前向傳播： 計算輸入數據通過神經網絡各層的輸出。
計算損失： 通過損失函數計算預測輸出與真實輸出之間的誤差。
反向傳播： 通過鏈式法則計算損失相對于每個權重的梯度。

反向傳播的詳細過程涉及鏈式法則在多層網絡中的應用，我們將這些步驟拓展到處理時間序列數據的BPTT算法中。

詳情見：BP神經網絡反向傳播原理【數學原理、舉例說明】

反向傳播通過時間（BPTT）算法

BPTT是一種針對循環神經網絡（Recurrent Neural Networks, RNNs）的訓練算法，它將標準反向傳播算法擴展到 時間序列數據 上。RNN的特點是其隱藏層不僅依賴于 當前的輸入 ，還依賴于 前一時間步的隱藏狀態 ，這使得RNN能夠處理序列數據。然而，這也引入了計算梯度的復雜性，因為損失不僅與當前時間步的輸出相關，還與之前時間步的隱藏狀態相關。

前向傳播

在BPTT中，前向傳播是從時間步1到時間步T逐步計算每個時間步的隱藏狀態和輸出。

假設我們有一個輸入序列 $\{x_1, x_2, \ldots, x_T\}$ ，每個 $x_t$ 是在時間步t的輸入。RNN的隱藏狀態 $h_t$ 和輸出 $y_t$ 依次計算如下：

初始化： 首先，隱藏狀態 $h_0$ 通常初始化為零或小的隨機值。
$h_0 = 0 \text{（或小的隨機值）}$
時間步1的計算：
- 計算隱藏狀態 $h_1$ ：
  $h_1 = f(W_{hx} x_1 + W_{hh} h_0 + b_h)$
  這里， $W_{hx}$ 是輸入到隱藏層的權重矩陣， $W_{hh}$ 是隱藏層到隱藏層的權重矩陣， $b_h$ 是偏置， $f$ 是激活函數（如tanh或ReLU）。這一步可以理解為將當前輸入 $x_1$ 與前一時間步的隱藏狀態 $h_0$ 結合，通過一個激活函數得到當前時間步的隱藏狀態 $h_1$ 。
  
  這與傳統BP（Backpropagation）不同，傳統BP不考慮時間步之間的依賴，而RNN通過引入隱藏層狀態的遞歸關系來捕捉 時間序列中的依賴性 。
- 計算輸出 $y_1$ ：
  $y_1 = g(W_{hy} h_1 + b_y)$
  這里， $W_{hy}$ 是隱藏層到輸出層的權重矩陣， $b_y$ 是輸出層的偏置， $g$ 是輸出層的激活函數（通常為softmax或線性函數）。這一步可以理解為將隱藏狀態 $h_1$ 轉化為輸出 $y_1$ 。
時間步t的計算（t=2, …, T）： 對于后續的每個時間步，我們重復上述步驟：
- 計算隱藏狀態 $h_t$ ：
  $h_t = f(W_{hx} x_t + W_{hh} h_{t-1} + b_h)$
  這里，隱藏狀態 $h_t$ 是當前輸入 $x_t$ 與前一時間步隱藏狀態 $h_{t-1}$ 的結合，通過激活函數 $f$ 得到。
- 計算輸出 $y_t$ ：
  $y_t = g(W_{hy} h_t + b_y)$
  輸出 $y_t$ 是當前隱藏狀態 $h_t$ 通過激活函數 $g$ 得到。

通過這一步步計算，我們將輸入序列 $\{x_1, x_2, \ldots, x_t\}$ 轉化為隱藏狀態序列 $\{h_1, h_2, \ldots, h_t\}$ 和輸出序列 $\{y_1, y_2, \ldots, y_t\}$ 。

為什么要將輸入序列轉換為隱藏狀態序列和輸出序列？

將輸入序列轉換為隱藏狀態序列和輸出序列的原因在于RNN的核心思想： 通過引入隱藏狀態，模型能夠捕捉序列數據中的時間依賴關系 。隱藏狀態序列 $\{h_1, h_2, \ldots, h_t\}$ 是RNN對輸入序列的內部表示，記錄了前一時間步的信息，并將其傳遞給當前時間步。

數學上，這種遞歸關系可以理解為狀態轉移函數：
$h_t = f(W_{hx} x_t + W_{hh} h_{t-1} + b_h)$
這個公式表示當前的隱藏狀態 $h_t$ 是當前輸入 $x_t$ 和前一時間步隱藏狀態 $h_{t-1}$ 的函數。通過這種遞歸關系，RNN能夠記住之前時間步的信息，并在后續時間步中使用，從而捕捉長時間的依賴關系。

輸出序列 $\{y_1, y_2, \ldots, y_t\}$ 是模型的預測結果，通過將隱藏狀態轉化為輸出，我們可以計算損失，并通過反向傳播更新模型參數。

計算損失

計算損失是為了衡量模型輸出與真實輸出之間的誤差。對于整個序列，我們通常采用均方誤差（MSE）或交叉熵損失。假設真實輸出序列為 $\{\hat{y}_1, \hat{y}_2, \ldots, \hat{y}_t\}$ ，損失函數 $L$ 可以表示為：

均方誤差（MSE）：
$\sum_{t=1}^T \frac{1}{2} (y_t - \hat{y}_t)^2$
這里，我們計算每個時間步的輸出 $y_t$ 與真實輸出 $\hat{y}_t$ 之間的平方誤差，并將所有時間步的誤差求和。
交叉熵損失：
$-\sum_{t=1}^T [\hat{y}_t \log(y_t) + (1 - \hat{y}_t) \log(1 - y_t)]$
這里，我們計算每個時間步的輸出 $y_t$ 與真實輸出 $\hat{y}_t$ 之間的交叉熵損失，并將所有時間步的損失求和。

反向傳播

反向傳播的目的是通過鏈式法則計算損失相對于每個權重的梯度，并更新權重。具體步驟如下：

計算輸出層的梯度：

$\delta^y_t = \frac{\partial \ell(y_t, \hat{y}_t)}{\partial y_t} \cdot g'(y_t)$
這里， $\delta^y_t$ 是第 t 時間步的輸出層梯度。這個公式中的每個部分代表：
- $\frac{\partial \ell(y_t, \hat{y}_t)}{\partial y_t}$ 是損失函數 $\ell$ 對輸出 $y_t$ 的導數，它表示輸出 $y_t$ 的變化對損失函數 $\ell$ 的影響。
- $g'(y_t)$ 是輸出層激活函數 $g$ 對其輸入 $y_t$ 的導數。

根據鏈式法則，我們計算 $\frac{\partial \ell}{\partial y_t}$ 時，需要考慮：
$\frac{\partial \ell}{\partial y_t} = \frac{\partial \ell}{\partial g(y_t)} \cdot \frac{\partial g(y_t)}{\partial y_t}$
這里， $\frac{\partial \ell}{\partial g(y_t)}$ 是損失函數對激活函數輸出的導數， $\frac{\partial g(y_t)}{\partial y_t}$ 是激活函數 $g$ 對輸入 $y_t$ 的導數。

計算隱藏層的梯度：
隱藏層的梯度計算涉及當前時間步和未來時間步的影響：
$\delta^h_t = \delta^y_t W_{hy}^T \cdot f'(h_t) + \delta^h_{t+1} W_{hh}^T \cdot f'(h_t)$
- $\delta^y_t W_{hy}^T \cdot f'(h_t)$ 是當前時間步輸出層梯度 傳播回來的部分。具體來說， $\delta^y_t$ 是輸出層梯度，通過輸出層到隱藏層的權重 $W_{hy}$ 傳遞回隱藏層，再乘以隱藏層激活函數 $f$ 的導數 $f'(h_t)$ 。
- $\delta^h_{t+1} W_{hh}^T \cdot f'(h_t)$ 是未來時間步隱藏層梯度 傳播回來的部分。這里， $\delta^h_{t+1}$ 是下一時間步的隱藏層梯度，通過隱藏層到隱藏層的權重 $W_{hh}$ 傳遞回當前隱藏層，再乘以當前隱藏層激活函數的導數 $f'(h_t)$
更新權重：
權重更新是通過梯度下降法進行的。梯度下降法的基本思想是沿著 梯度的反方向 更新權重，使得損失函數逐漸減小。
- 輸入到隱藏層的權重更新：
  $\Delta W_{hx} = \sum_{t=1}^T \delta^h_t \cdot x_t^T$
  這里， $\delta^h_t$ 是時間步 $t$ 的隱藏層梯度， $?xtT? \cdot x_t^T$ 表示輸入 $x_t$ 的轉置。我們將所有時間步的梯度相加，得到輸入到隱藏層權重的更新量。
- 隱藏層到隱藏層的權重更新：
  $\Delta W_{hh} = \sum_{t=2}^T \delta^h_t \cdot h_{t-1}^T$
  這里， $\delta^h_t$ 是時間步 $t$ 的隱藏層梯度， $?ht?1T? \cdot h_{t-1}^T$ 表示前一時間步隱藏狀態 $h_{t-1}$ 的轉置。同樣地，我們將所有時間步的梯度相加，得到隱藏層到隱藏層權重的更新量。
- 隱藏層到輸出層的權重更新：
  $\Delta W_{hy} = \sum_{t=1}^T \delta^y_t \cdot h_t^T$
  這里， $\delta^y_t$ 是時間步 $t$ 的輸出層梯度， $?htT? \cdot h_t^T$ 表示當前時間步隱藏狀態 $h_t$ 的轉置。我們將所有時間步的梯度相加，得到隱藏層到輸出層權重的更新量。

這些權重更新公式通過鏈式法則計算各個權重的梯度，并使用梯度下降法更新權重，使得損失函數最小化。

梯度消失和梯度爆炸問題

在BPTT中，梯度消失和梯度爆炸是兩個主要問題。這兩個問題都與梯度在時間步長上的傳播有關。隨著時間步數增加，梯度的值可能會逐漸減小到幾乎為零（梯度消失）或變得非常大（梯度爆炸），這會影響模型的訓練效果。

梯度消失

隨著時間步數的增加，梯度逐漸減小，最終可能變得非常接近于零。這導致模型無法有效更新權重，無法捕捉到長期依賴關系。

數學上，如果激活函數的導數 $f'(h_t)$ 小于 1，多次相乘后會趨近于零。
比如，激活函數為 $\tanh$ ，它的導數值在 [-1, 1] 之間，且通常小于 1。

梯度爆炸

隨著時間步數的增加，梯度逐漸變大，最終可能變得非常大。這導致權重更新過大，模型無法收斂。

數學上，如果激活函數的導數 $f'(h_t)$ 大于 1，多次相乘后會迅速增長。
比如，激活函數為 ReLU（修正線性單元），其導數在正區間為 1，如果某些參數或權重較大，梯度可能會迅速累積變大。

梯度傳播過程中的數學推導

假設一個簡單的RNN模型，隱藏層激活函數為 $f$ ，我們考慮隱藏層的狀態 $h_t$ 及其梯度的傳播過程。

基本概念和公式

隱藏層狀態更新：
$h_t = f(W_{hh} h_{t-1} + W_{hx} x_t + b_h)$
輸出層狀態：
$y_t = g(W_{hy} h_t + b_y)$
損失函數：
$\mathcal{L} = \sum_{t=1}^T \ell(y_t, \hat{y}_t)$
輸出層梯度：
$\delta^y_t = \frac{\partial \ell(y_t, \hat{y}_t)}{\partial y_t} \cdot g'(y_t)$

梯度傳播到隱藏層

我們通過鏈式法則計算隱藏層梯度。首先從輸出層梯度開始傳播，考慮激活函數 $f$ 的導數 $f'(h_t)$ 。

隱藏層梯度的遞歸公式為：

$\delta^h_t = \delta^y_t W_{hy}^T \cdot f'(h_t) + \delta^h_{t+1} W_{hh}^T \cdot f'(h_t)$

假設激活函數 $f$ 的導數在所有時間步長上都是一個常數 $k$ ，即 $f'(h_t) = k$ 。為了簡化，我們假設權重矩陣 $W_{hh}$ 和 $W_{hy}$ 也為常數。

梯度遞歸公式的展開

我們從最后一個時間步 $T$ 開始，逐步向前展開遞歸公式：

$\delta^h_T = \delta^y_T W_{hy}^T \cdot k$

對于 $T ? 1$ 時間步：

$\delta^h_{T-1} = \delta^y_{T-1} W_{hy}^T \cdot k + \delta^h_T W_{hh}^T \cdot k$

將 $\delta^h_T$ 帶入：
$\delta^y_{T-1} W_{hy}^T \cdot k + (\delta^y_T W_{hy}^T \cdot k) W_{hh}^T \cdot k$
$\delta^y_{T-1} W_{hy}^T + k^2 \delta^y_T W_{hy}^T W_{hh}^T$

我們繼續展開 $T ? 2$ 時間步：

$\delta^h_{T-2} = \delta^y_{T-2} W_{hy}^T \cdot k + \delta^h_{T-1} W_{hh}^T \cdot k$
$\delta^y_{T-2} W_{hy}^T \cdot k + \left( \delta^y_{T-1} W_{hy}^T \cdot k + \delta^h_T W_{hh}^T \cdot k \right) W_{hh}^T \cdot k$
$\delta^y_{T-2} W_{hy}^T \cdot k + \delta^y_{T-1} W_{hy}^T W_{hh}^T \cdot k^2 + \delta^y_T W_{hy}^T W_{hh}^T W_{hh}^T \cdot k^3$

推廣到一般情況，對于時間步 ( t )：

$\delta^h_t = \delta^y_t W_{hy}^T \cdot k + \delta^h_{t+1} W_{hh}^T \cdot k$

遞歸展開后，我們可以看到梯度會逐步乘以 ( k )，并傳播到前面的時間步。這意味著：

$\delta^h_t = \delta^y_t \cdot (W_{hy}^T \cdot k^t)$

推導公式

假設 $W_{hy}$ 和 $W_{hh}$ 為單位矩陣 $I$ ，我們簡化得到：

$\delta^h_t = \delta \cdot k^t$

如果激活函數的導數 $k < 1$ ，那么 $k^t$ 會隨著 $t$ 增加而快速趨近于零，導致梯度消失。

具體示例

為了更直觀地理解梯度消失和梯度爆炸，我們用一個簡單的RNN模型和一個假設的初始梯度進行解釋。

假設：

輸入序列長度為 ( T )。
隱藏層激活函數為 ( $\tanh$ )。
初始梯度為 ( $\delta = 1$ )。
每一步的激活函數導數 ( $f'(h_t) = k$ )（假設為常數）。

梯度消失示例

假設激活函數導數 $k = 0.5$ ，即每一步的導數都小于 1。

隨著時間步數 $T$ 的增加，梯度會逐漸減小：

$\delta^h_T = \delta \cdot k^T$

例如，當 $T = 10$ 時：

$\delta^h_{10} = 1 \cdot 0.5^{10} = 1 \cdot 0.00098 = 0.00098$

可以看到，梯度非常小，接近于零。

更進一步，如果 $T = 20$ ：

$\delta^h_{20} = 1 \cdot 0.5^{20} = 1 \cdot 0.00000095 = 0.00000095$

梯度幾乎為零，說明模型無法有效更新權重，導致無法捕捉長期依賴關系。

梯度爆炸示例

假設激活函數導數 $k = 1.5$ ，即每一步的導數都大于 1。

隨著時間步數 $T$ 的增加，梯度會逐漸增大：

$\delta^h_T = \delta \cdot k^T$

例如，當 $T = 10$ 時：

$\delta^h_{10} = 1 \cdot 1.5^{10} = 1 \cdot 57.67 = 57.67$

可以看到，梯度非常大，導致訓練不穩定。

更進一步，如果 $T = 20$ ：

$\delta^h_{20} = 1 \cdot 1.5^{20} = 1 \cdot 33252.32 = 33252.32$

梯度變得非常大，說明模型無法收斂，權重更新會過大，導致訓練失敗。

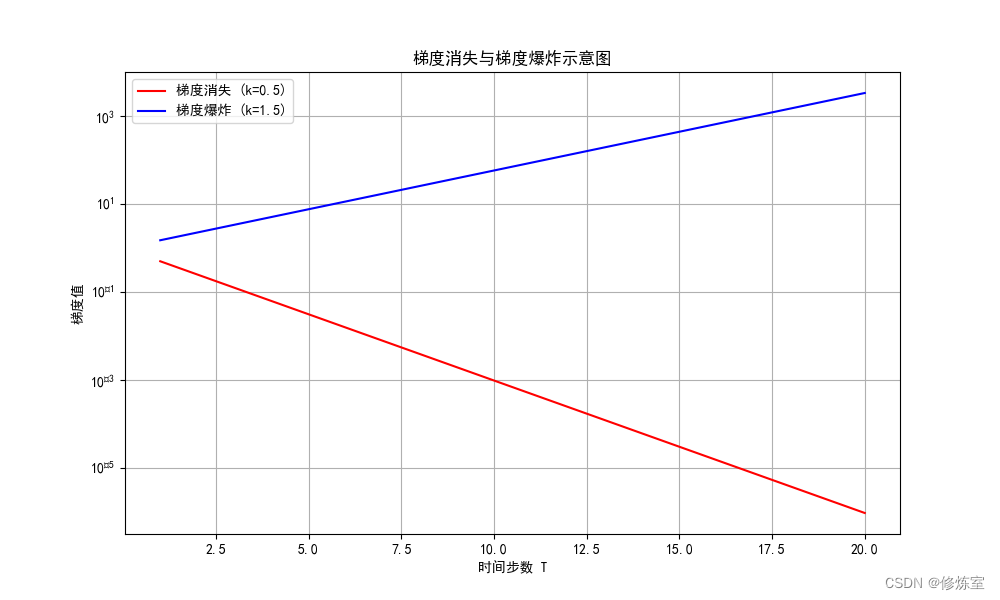
在這里插入圖片描述

梯度消失：圖中紅線表示的梯度隨著時間步數 𝑇 增加而快速減小，趨近于零。這說明當時間步數增加時，梯度值變得非常小，無法有效更新權重，導致模型無法捕捉長期依賴關系。
梯度爆炸：圖中藍線表示的梯度隨著時間步數 𝑇 增加而快速增大。這說明當時間步數增加時，梯度值變得非常大，導致權重更新過大，訓練過程變得不穩定，模型難以收斂。

解決梯度消失和梯度爆炸的方法

為了緩解梯度消失和梯度爆炸問題，可以采用以下幾種常見的方法：

梯度裁剪（Gradient Clipping）：
- 將梯度的絕對值限制在某個閾值范圍內，防止梯度爆炸。
- 例如，當梯度超過某個閾值時，將其裁剪到這個閾值。
正則化方法：
- 使用L2正則化（權重衰減）防止過度活躍的神經元。
- 增加權重更新時的懲罰項，控制權重值不至于過大。
批歸一化（Batch Normalization）：
- 對每個時間步的隱藏狀態進行歸一化，穩定訓練過程。
- 通過歸一化，控制每個時間步的輸出范圍，防止梯度過大或過小。
調整激活函數：
- 選擇適當的激活函數（如ReLU、Leaky ReLU等），防止梯度消失和爆炸。
- 例如，Leaky ReLU 在負區間也有非零導數，避免了完全的梯度消失問題。

為什么很小的梯度無法更新權重并導致無法捕捉長期依賴關系？

當梯度非常小時，反向傳播的權重更新公式：

$\Delta W = -\eta \cdot \frac{\partial \mathcal{L}}{\partial W}$

梯度項 $\frac{\partial \mathcal{L}}{\partial W}$ 會非常小。這里， $\eta$ 是學習率。當梯度接近零時，權重更新 $\Delta W$ 也會接近零。這意味著神經網絡的權重幾乎不會發生變化，導致模型無法從訓練數據中學習到有用的信息，從而無法有效捕捉長期依賴關系。