一、遞歸

1.遞歸的概念

遞歸是學習C語言函數繞不開的一個話題，那什么是遞歸呢? 遞歸其實是一種解決問題的方法。在C語言中，遞歸就是函數自己調用自己。

2.遞歸的思想

遞歸就是：把一個大型復雜的問題層層轉化為一個與原問題相似的，但規模較小的子問題來求解。直到子問題不能再被拆分，遞歸就結束了。所以遞歸的思想就是把大事化小的過程。遞歸中的遞就是遞推的意思，歸就是回歸的意思。

3.遞歸的限制條件

遞歸在書寫的時候，有2個必要條件:
● 遞歸存在限制條件，當滿足這個限制條件的時候，遞歸便不再繼續。
● 每次遞歸調用之后越來越接近這個限制條件。

二、遞歸的一些典型例子

1.求一個數的階乘

#include <stdio.h>
int fac(int n)
{if (n == 1||n == 0)return 1;elsereturn n * fac(n-1);
}
int main()
{int n = 0;scanf("%d", &n);int ret = fac(n);printf("%d的階乘是%d\n",n,ret);return 0;
}

運行結果：
上面通過函數遞歸來求一個正整數的階乘，那具體要怎么理解上面的代碼呢？分析：一個正整數的階乘(factorial)是所有小于及等于該數的正整數的積，即n的階乘公式為 n=n*(n-1)! 并且0的階乘為1。自然數n的階乘寫作 n!。例如：

5! = 5*4*3*2*1
4! = 4*3*2*1
所以 5! = 5*4!

這樣的思路就是把一個較大的問題，轉換為一個與原問題相似，但規模較小的問題來求解的。當n==1或者n==0的時候，n的階乘是1，其余n的階乘都是可以通過公式計算。
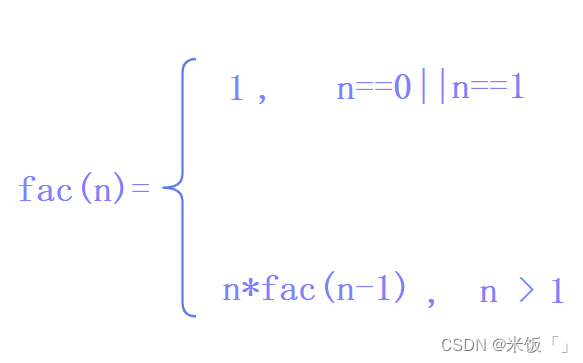那我們就可以寫出函數fac求n的階乘，假設fac(n)就是求n的階乘，那么fac(n-1)就是求n-1的階乘。所以構造的函數就是上面的fac。
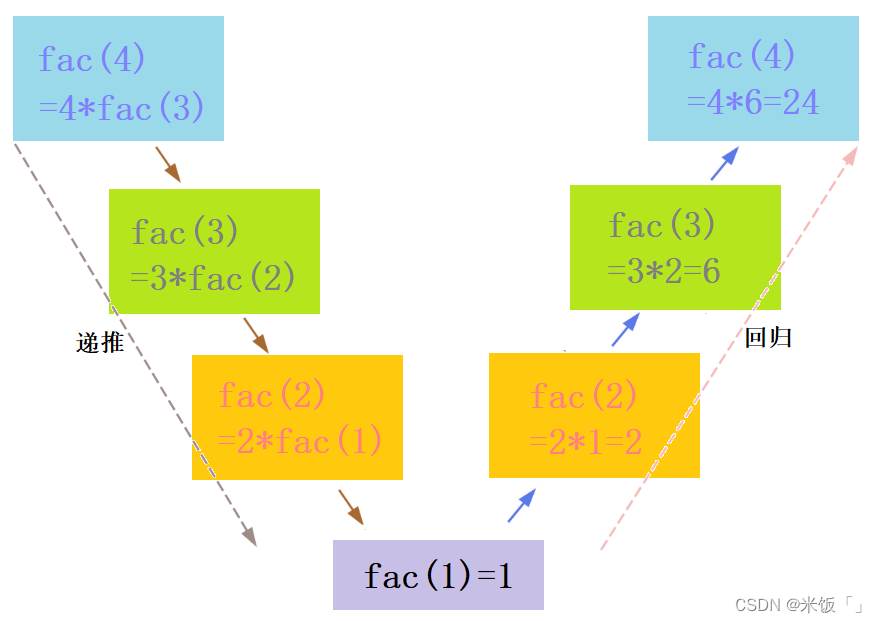就是因為遞歸存在限制條件，這就使得函數自己調用自己時，會有結束的時候。當一個復雜的問題被拆解到不能再拆解的子問題時，我們一眼就能看出子問題的答案。而求解出子問題的答案后，我們就能逐一求解上一層的子問題，以至于就能求解出原問題的答案了。

2.順序打印一個整數的每一位

輸入一個整數n，按照順序打印整數的每一位。比如：
1.輸入: 1234，輸出：1 2 3 4
2.輸入: 520，輸出：5 2 0

#include <stdio.h>
void Print(int n)
{if (n > 9)Print(n / 10);printf("%d ", n % 10);
}
int main()
{int n = 0;printf("請輸入一個整數：");scanf("%d", &n);Print(n);return 0;
}

運行結果：
這里需要知道一個知識點：在C語言中，整數除以一個整數，得到的還是整數，因為小數部分被丟棄掉了。
①在C語言中，一個整數除以10以后，這個整數的個位會被去掉，得到個位前面的整數部分。比如：327/10得到結果是32，去掉了個位上的7。一個整數除以10以后，位數會減少一位。
②一個整數模(%)上10以后得到的是個位上的數字，比如：43%10得到的結果為3，即余數就為3。

那怎么理解上面的代碼呢？
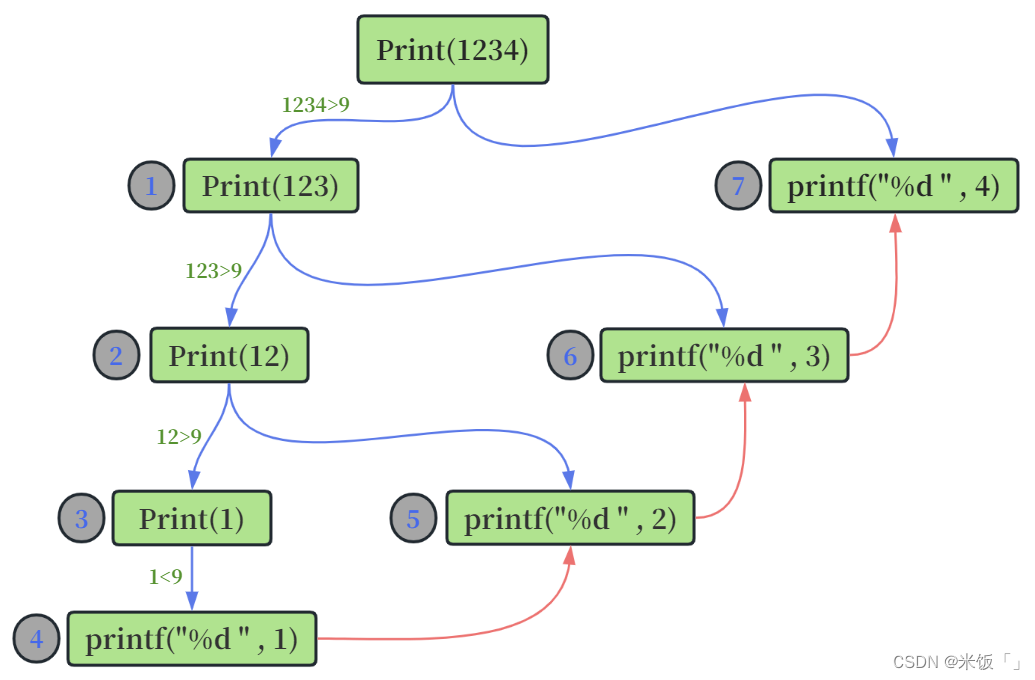
對于這個函數，如果傳進去的實參為1234，進入函數就先判斷n是否大于9，如果n大于9，就將n/10傳給Print函數，這里就又調用了Print函數，直到n的值小于等于9以后，if語句不成立了，就執行printf("%d " , n%10)這條語句，即先打印1234的最高位1，然后返回上一層繼續打印百位的2，然后再返回上一層打印十位上的3，最后返回第一層打印個位上的4。

圖解釋：

3.漢諾塔

先學習一下什么是漢諾塔(河內塔)? 漢諾塔是一個起源于印度古老傳說的益智游戲，由法國數學家愛德華·盧卡斯于1883年發明。
漢諾塔的玩法：對于上面的三個木樁，中間的木樁上疊放有圓盤，而且是按照小圓盤在大圓盤上方的次序疊放的。玩法是將一個木樁上的圓盤移動到另一個木樁上。

移動規則：
● 1.一次只能移動一個圓盤
● 2.每個木樁上只有最頂層的圓盤可以移動，并且所移動的圓盤只能移動到空木樁上或者是它要比木樁頂層已存在的圓盤小。也就是說，你每移動一次圓盤，不管在哪根木樁上都要保證小圓盤在大圓盤的上方。

我們從最簡單的情況開始逐一講解：
Ⅰ.如果木樁上只有一個圓盤的時候，要把A柱上的圓盤移動到C柱上，直接拿過去就好了。A→C

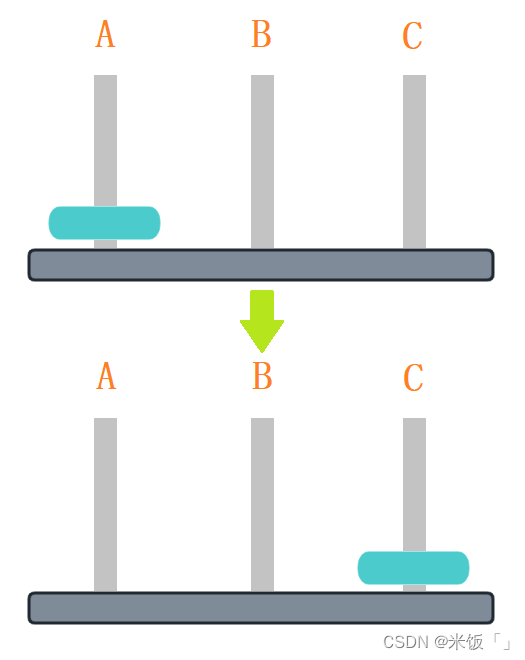
Ⅱ.如果A木樁上有兩個圓盤，現在要把A木樁上的圓盤移動到C木樁上，就需要借助B樁移動三次圓盤。
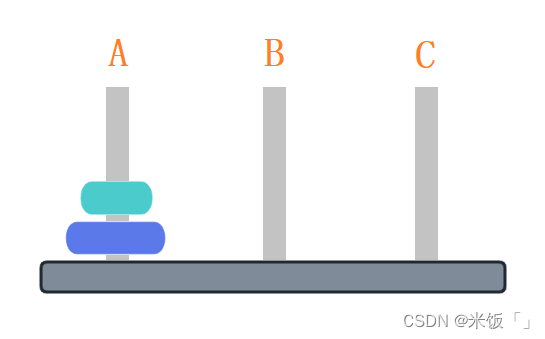共需三步：A→B，A→C，B→C

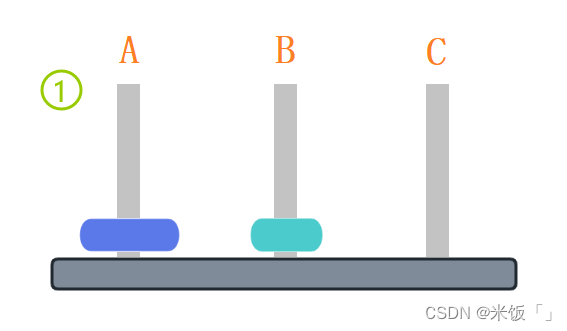
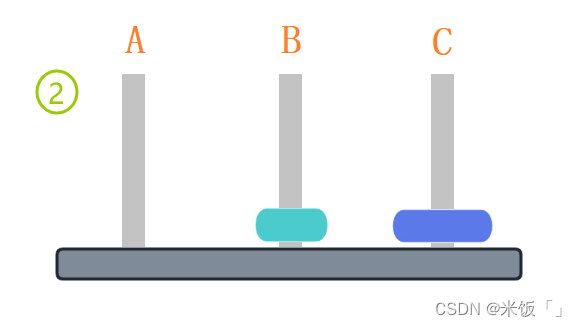
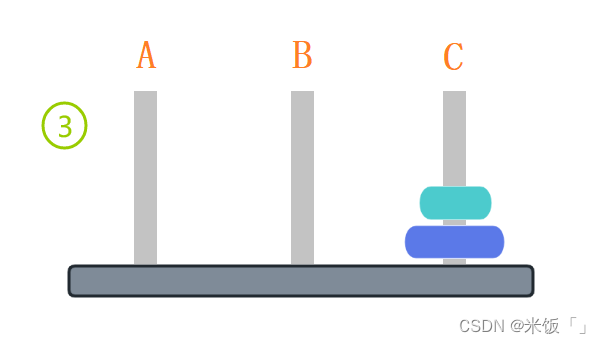
Ⅲ.如果A木樁上有三個圓盤，現在要把A木樁上的圓盤移動到C木樁上最少需要移動多少次圓盤呢？
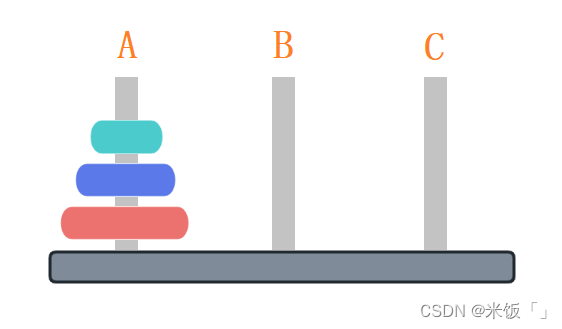答案是最少需要7步：A→C，A→B，C→B，A→C，B→A，B→C，A→C
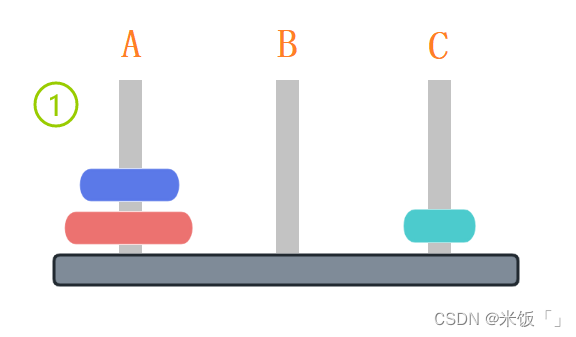
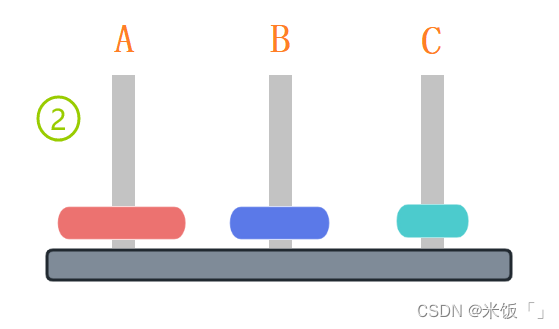
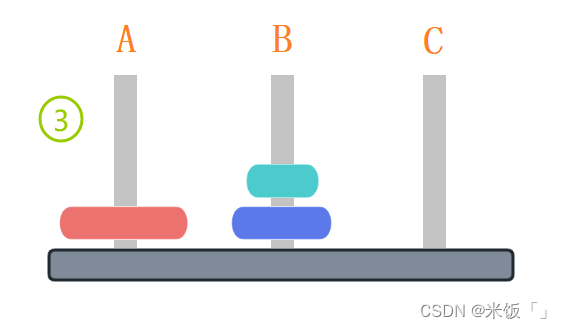
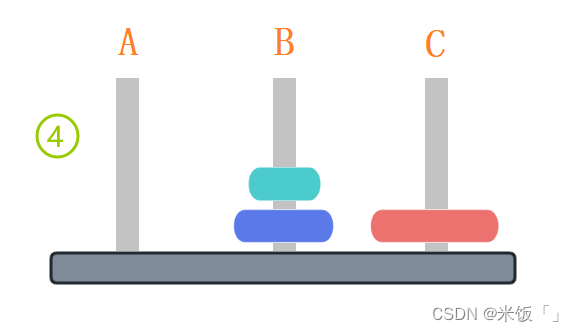到第四步完以后發現，最大的那個圓盤已經放在C柱上了，剩下的兩個圓盤要放到C柱上，其實就和上面只有兩個圓盤的情況是一樣的了，只是這里要借助A木樁移動到C木樁上，位置不一樣，但是移動的次數和兩個圓盤情況下是一樣的。上面的4步加上只有兩個圓盤情況下的3步，最少只需要7步就能把A柱上的圓盤移動到C柱上。

其實通過上面的1~3層圓盤的漢諾塔移動情況的分析，不難發現這里就有遞歸的思想。像只有兩個圓盤的情況：我們要把A柱上最大的那個圓盤先移動到C柱上，就要先把A柱上較小的圓盤先轉移到B柱上，然后才能把較大的那個圓盤移動到C柱上。然后你會發現剩下的那個較小的圓盤要移動到C柱上，就跟柱子上只有一個圓盤的情況是一樣的，只需要移動一步即可。同理：A柱上如果有三個圓盤的情況，當把最大的那個圓盤移動到了C柱上以后，剩下的兩個較小圓盤要移動到C柱上，移動的次數就跟柱子上只有兩個圓盤的情況是一樣的，只是借助的柱子不一樣而已。那代碼要怎么實現呢？

#include <stdio.h>
//1.構造一個用來打印移動軌跡的函數
void Print_Movetrack(char ori, char des)
{static int time = 0;//定義一個靜態變量，用來記錄移動的次數printf("第%d步:%c-→%c\n", ++time, ori, des);
}
//2.漢諾塔代碼的遞歸邏輯
void Hanoi(int n, char a, char b, char c)
{if (n == 1){Print_Movetrack(a, c);}else{Hanoi(n - 1, a, c, b);//Ⅰ將A柱上最大圓盤上方的n-1個圓盤借助C柱移動到B柱上Print_Movetrack(a, c);//Ⅱ將最大的圓盤從A柱移動到C柱上Hanoi(n - 1, b, a, c);//Ⅲ將剛才移動到B柱上的圓盤借助A柱移動到C柱上}
}
int main()
{int n = 0;printf("請輸入圓盤個數：");scanf("%d", &n);Hanoi(n, 'A', 'B', 'C');//n是圓盤個數；A,B,C是三根木樁的編號return 0;
}

運行結果：
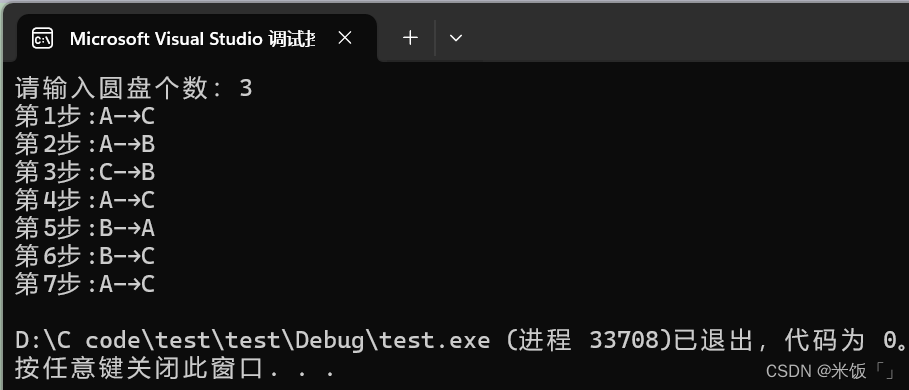
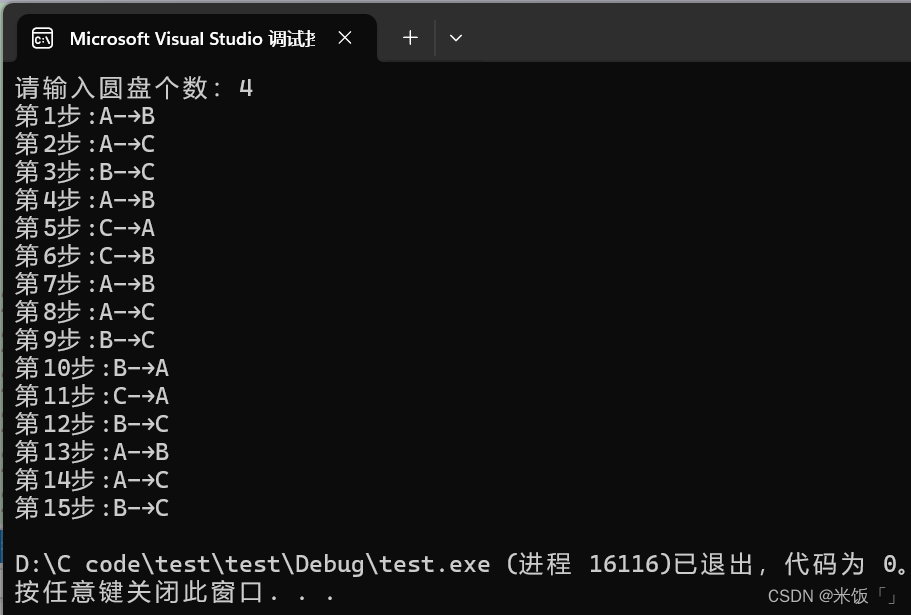最難理解的是這個函數是怎么構造出來的，遞歸的邏輯是什么？但是也緊扣遞歸的限制條件，函數里面有使這個遞歸結束的限制條件，每一次遞歸，都會越來越接近這個限制條件。
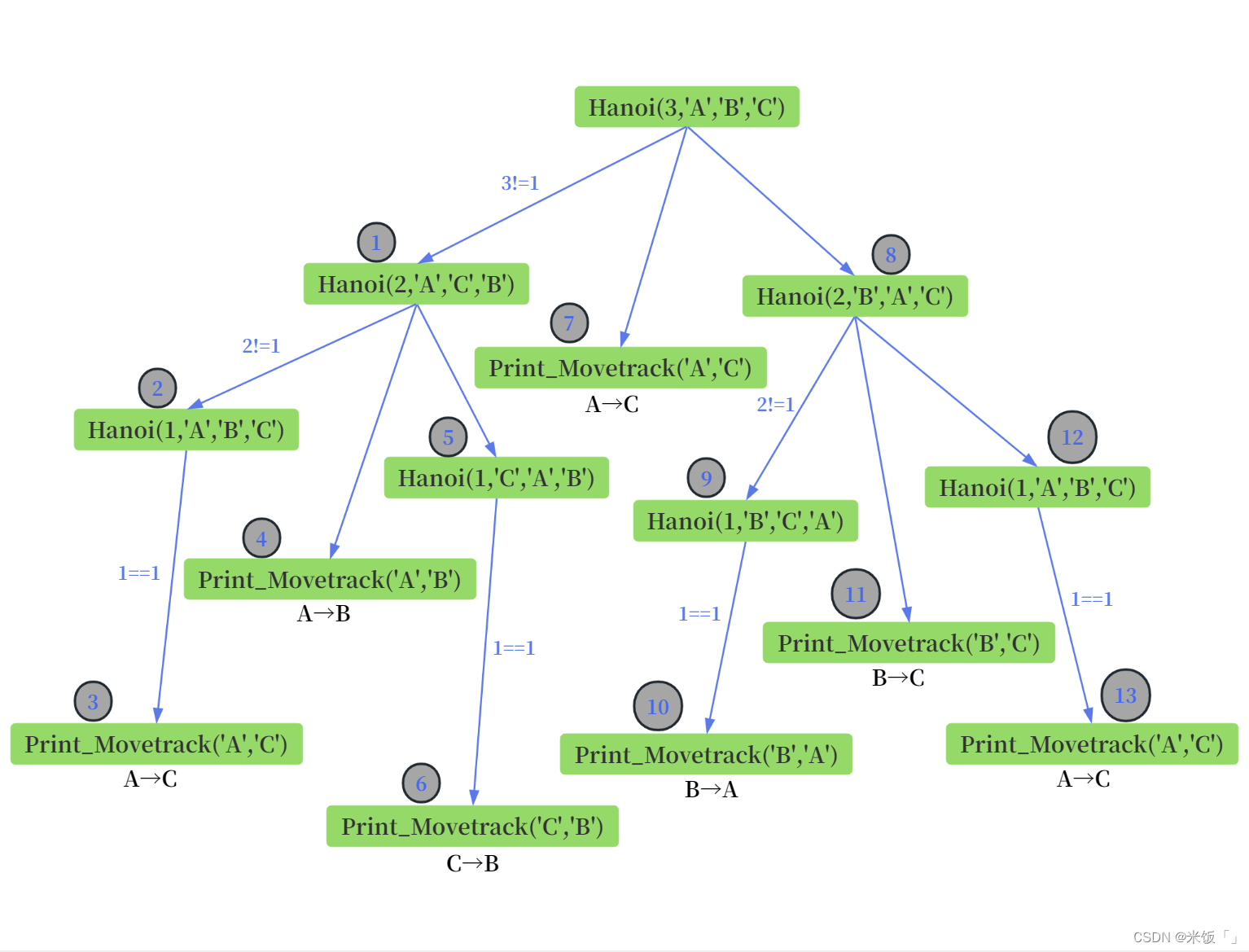
我們以A柱上有3個圓盤的情況來說明上面代碼的遞歸邏輯：函數在逐層調用自己時，當滿足限制條件后，會逐一返回上一層繼續執行上一層后續的代碼。

4.青蛙跳臺階

青蛙跳臺階問題是啥？這個問題描述的是：一只青蛙去跳臺階，它一次可以跳1個臺階，一次也可以跳2個臺階。
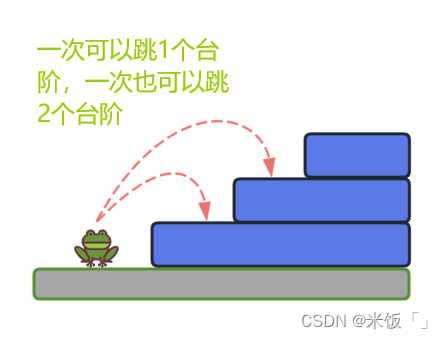問：如果現在有n層臺階，青蛙要跳上這n層臺階，共有多少種跳法？
分析：
Ⅰ.當只有一層臺階(n=1)的時候，青蛙只能跳1個臺階，只能跳一次。如圖所示：
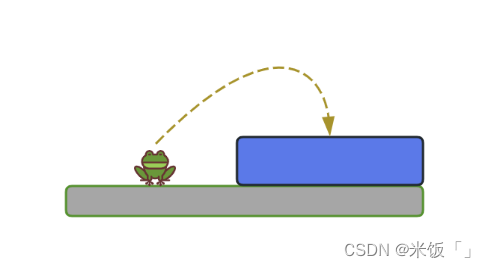Ⅱ.當有兩層臺階(n=2)的時候，青蛙要跳上這兩層臺階，共有2種跳法。一是每次跳1個臺階，共兩次跳完；二是一次跳2個臺階，一次就跳完。如下圖：
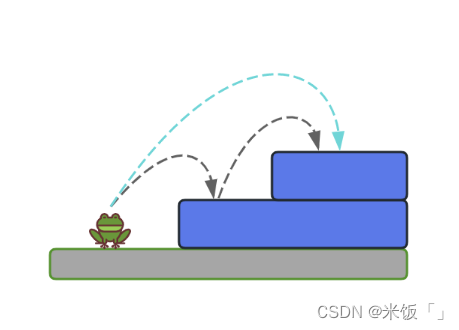Ⅲ.當有三層臺階(n=3)的時候，要怎么算有多少種跳法呢？首先分析一下：青蛙一開始一次，要么跳1個臺階，要么跳2個臺階。
①如果青蛙一開始一次跳了1個臺階，那么就還剩下兩層臺階，那這兩層臺階的跳法，就跟上面只有兩層臺階(n=2)的跳法是一樣的，共有2種。
②如果青蛙一開始一次跳了2個臺階，那么就還剩下一層臺階，這一層臺階的跳法就跟只有一層臺階(n=1)的跳法一樣，只有一種。
所以綜上所述，三層臺階的跳法總共有3種。就等于1層臺階和2層臺階的跳法總和。如下圖所示：
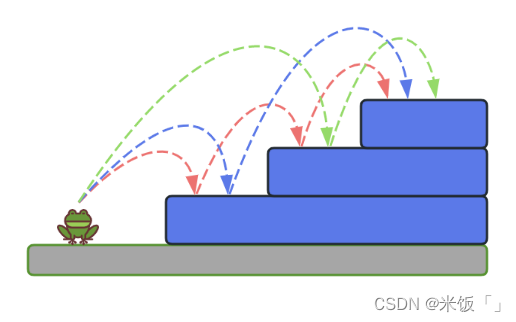Ⅳ.當有四層臺階(n=4)的時候，也是看青蛙一開始是怎么跳的，如果一開始青蛙跳了1個臺階，那后面就還剩三層臺階，就跟上面只有三層臺階(n=3)的跳法是一樣，有3種跳法。如果一開始青蛙跳了2個臺階，就還剩下兩層臺階，跟上面只有兩層臺階(n=2)的跳法一樣，有2種跳法。所以對于四層臺階，總共有5種跳法。就等于2層臺階和3層臺階的跳法總和。
Ⅴ.依次類推，如果青蛙要跳上n層臺階，這n層臺階的跳法就等于(n-2)層臺階和(n-1)層臺階的跳法總和。規律就是：
C語言代碼的實現：

#include <stdio.h>
int Step(int n)
{if (n == 1)return 1;else if (n == 2)return 2;elsereturn Step(n - 2) + Step(n - 1);
}
int main()
{int step_num = 0;printf("請輸入臺階層數：");scanf("%d", &step_num);printf("%d層臺階共有%d種跳法\n",step_num , Step(step_num));
}

運行結果：
我們把逐層臺階的跳法數量整理出來看：
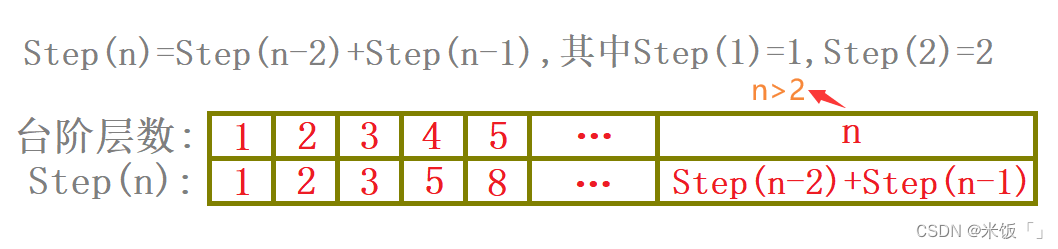通過上面的表也可以直觀的看出來，青蛙跳臺階的種數算法怎么計算，第n層臺階跳法就等于n-2層臺階和n-1層臺階的跳法總和。

5斐波那契數列

先介紹一下斐波那契數列：
斐波那契數列又稱黃金分割數列，是由意大利數學家萊昂納多·斐波那契以兔子繁殖為例而引入的，故稱為兔子數列。這個問題是：兔子在出生兩個月以后，就有繁殖能力了，成熟以后的一對兔子每個月都能生出一對小兔子，如果所有的兔子都不死，那么問在一年以后可以繁殖多少對兔子？

我們拿一對剛剛出生的兔子來分析：
①剛出生的一對小兔子第一個月還沒有繁殖能力，所以第一個月是一對兔子。
②兩個月以后生下一對小兔子，所以現在共有兩對小兔子。
③第三個月后，老兔子又生下一對兔子，上個月新生的那一對兔子還沒有繁殖能力，所以現在一共有3對兔子。
④第四個月后，老兔子繼續生下一對小兔子，剛剛成熟的一對兔子也生下一對小兔子，加上老兔子上個月剛出生的一對兔子現在一共就有5對兔子。
…
畫出過程圖來說明：
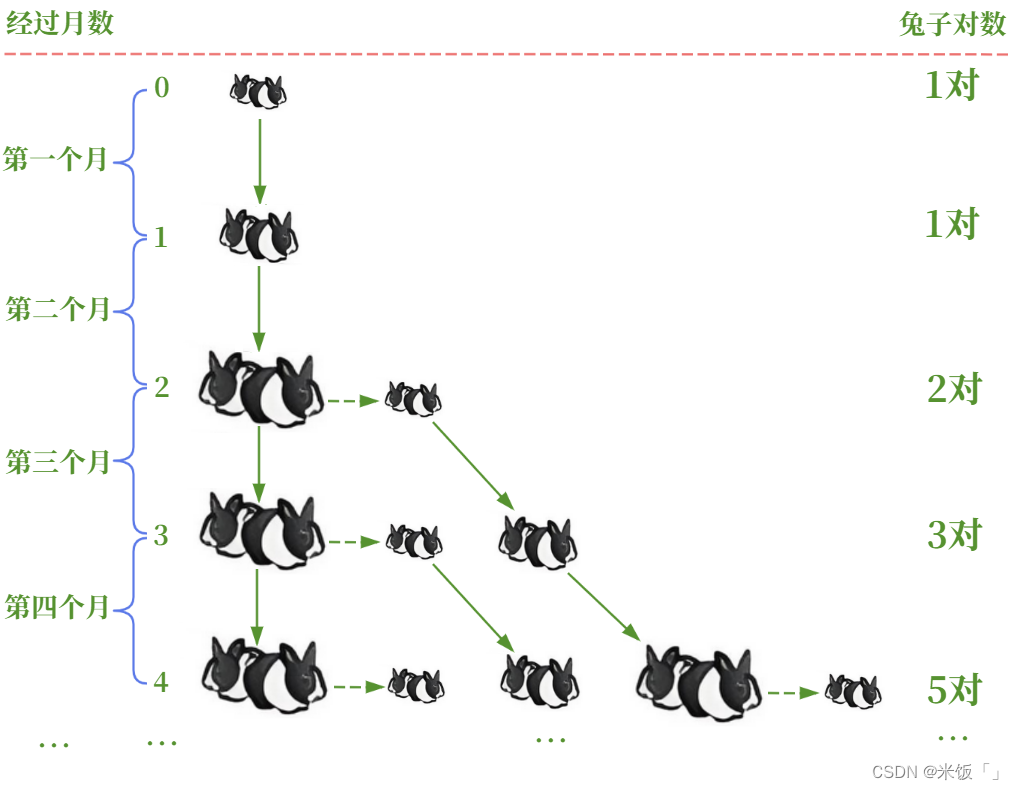上圖經過月份那里有一個0，你可以理解為兔子剛出生的時刻。注意圖中寫的是經過的月份，不是實際月份，不要理解錯誤。所以通過上圖可以直觀的看出兔子繁殖對數的規律：
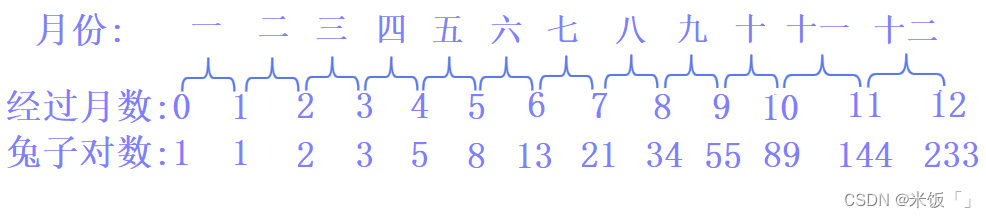由表可以看出從第三月起，每個月的兔子對數是前兩個月的兔子對數之和。由此給出斐波那契數列的定義：一個數列從第三項起，每一項都等于前兩項之和，即1 1 2 3 5 8 13 21…這樣一個數列。那遞歸的邏輯在這里就可以理解了，那求第n個斐波那契數的代碼實現：

#include <stdio.h>
//斐波那契數的遞歸邏輯
int Fib(int n)
{if (n == 1 || n == 2)return 1;elsereturn Fib(n - 2) + Fib(n - 1);}
int main()
{int n = 0; //這個n表示的是斐波那契數列中的第幾項scanf("%d", &n);printf("第%d項斐波那契數為%d\n", n , Fib(n));return 0;
}

運行結果：
所以在第12個月的時候(還沒有經過十二月)，總共有144對兔子，即288只兔子。如果是一年以后，那就要經過十二月，到下一年的一月開頭，那就有233對兔子，即有466只兔子。

遞歸和迭代的對比

上面的青蛙跳臺階和斐波那契數列是非常相似的，但是對于斐波那契數列是不適合使用遞歸的方法來實現。當我們要求的斐波那契數列的項數很大時，比如我們要求第50項斐波那契數時，這個遞歸所花費的時間是非常長的，為什么呢？看下面的遞歸邏輯圖：
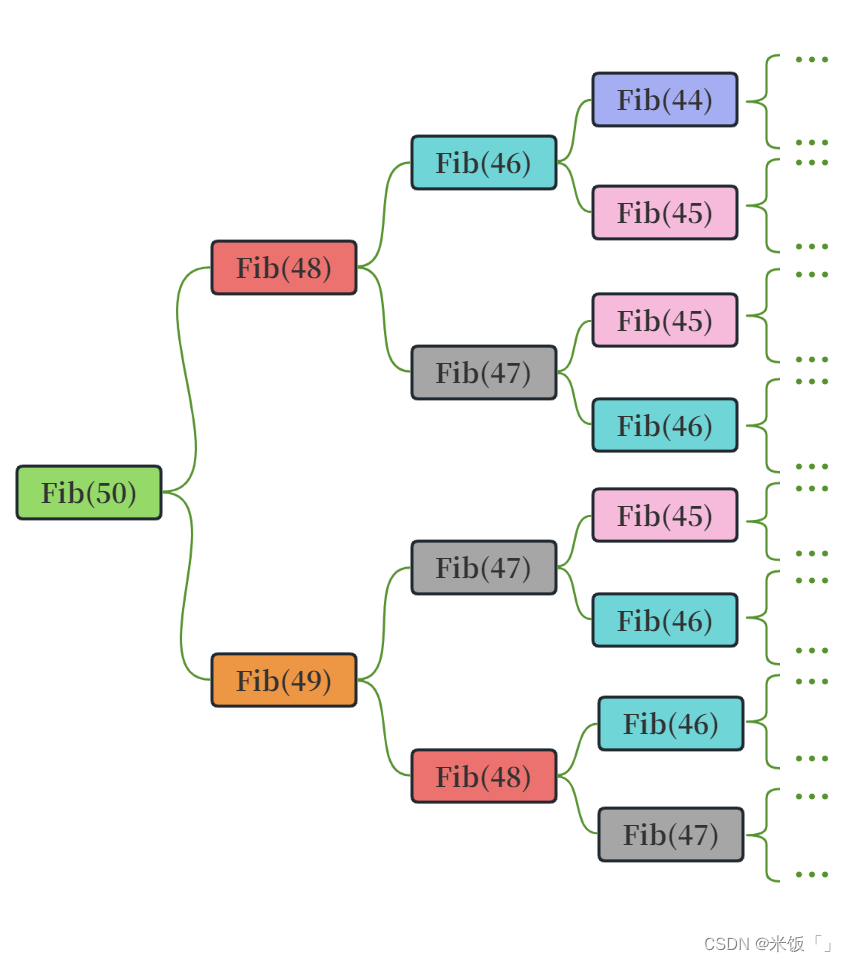從上圖可以看出，遞歸程序會不斷的展開，在展開的過程中，我們很容易就能發現，在遞歸的過程中會有重復計算，而且遞歸層次越深，冗余計算就會越多。如果采用非遞歸的方式(迭代)，效率就可以大大提高：

#include <stdio.h>
int Fib(int n)
{int a = 1;int b = 1;int c = 1;while (n > 2){c = a + b;a = b;b = c;n--;}return c;
}
int main()
{int n = 0;while (scanf("%d", &n) != EOF){int ret = Fib(n);printf("第%d項斐波那契數為%d\n", n, ret);}return 0;
}

運行結果：
上面的這種求第幾項斐波那契數的方法就是迭代法。每一次對過程的重復稱為一次"迭代"，而每一次迭代得到的結果將會作為下一次迭代的初始值。這種就叫做迭代法，也稱為輾轉法。所以不是所有的問題都適合用遞歸的方法。

Ⅰ.遞歸的優缺點
優點：
● 可以將大問題轉化為小問題，減少代碼量。
● 可以去掉不斷重復的代碼，使代碼精簡，提升可讀性。
缺點：
● 遞歸調用浪費空間，遞歸太深還容易造成堆棧溢出。

Ⅱ.迭代的優缺點
優點：
● 可以將重復的問題轉化為一單問題的重復操作，減少代碼量。
● 代碼運行效率高，時間只因為循環次數的增加而增加，沒有額外的內存空間開銷。
缺點：
● 代碼不如遞歸簡潔，有時可能不容易理解。