題目

兩個隨機變量x和y，如果聯合PDF分解為：

那么稱他們為條件獨立的。在上式中z是條件隨機變量。

我們觀察

其中, ,?是相互獨立的。證明和是條件獨立的。給出條件變量是A。和是無條件獨立么？也就是

成立么？為了回答這個問題，考慮, ,?是獨立且都有PDF N(0,1)

解答

參考（10-7），當A是條件時可以得到：

由獨立的性質：

可以到

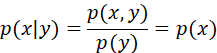
因此當, 是相互獨立時，得到：

由于,?是相互獨立的，因此：

也就是和是條件獨立的

---

如果要驗證和是否無條件獨立，只需要計算：

由于

因此：

于是：

由, , 是相互獨立，因此：

而由于：

因此：

因此：與不獨立

---

當然，另外一種邏輯，就是驗證是否可以拆成和的乘積形式。

此時考慮：

根據多元高斯分布性質（多元高斯分布（Multivariate Gaussian Distribution）（詳細說明，便于理解）-CSDN博客），得到:

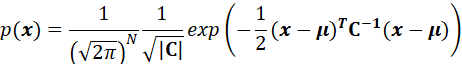
其中：

?

根據上面計算，其中，而：

再利用, 是相互獨立，且服從N

因此：

用同樣的方式獲得后，可以得到：

因此，可以得到：

于是中的可以化簡為：

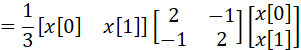
顯然，上式無法因式分解成僅包含和的獨立項，也就是無法拆分成和的乘積項，因此

不成立。也就是和不是無條件獨立