簡介:
在科學和工程中,我們經常遇到描述事物變化的微分方程。這些方程可以幫助我們理解從行星運動到藥物在體內的擴散等各種現象。但是,很多微分方程非常復雜,手動求解幾乎不可能。這時,我們就可以使用像 ode45這樣的工具來幫助我們找到解決方案。下面談談ode45函數的基本用法以及簡單應用。
一、ode45()概念與用法
ode45?是 MATLAB 中用于求解常微分方程初值問題的函數,它采用了一種稱為 “Runge-Kutta 方法” 的數值積分技術。具體來說,ode45?使用了一種稱為 “Dormand-Prince” 方法的五階龍格-庫塔公式,同時還使用了一個自適應步長控制算法,以保證數值解的精度和穩定性。
ode45?的基本用法如下:
[t, y] = ode45(@odefun, tspan, y0)@odefun?是一個函數句柄,表示待求解的微分方程組。這個函數接受兩個參數:時間?t?和狀態向量?y,并返回對應的導數值。tspan?是一個包含兩個元素的數組,表示求解的時間區間?[t_start, t_end]。y0?是一個包含微分方程組初始狀態的列向量。
ode45?返回兩個輸出參數:
t?是一個列向量,包含求解過程中的時間點。y?是一個大小為?(length(t), length(y0))?的矩陣,每一行表示對應時間點?t?處的狀態向量?y。
二、ode45()步驟流程方法
使用 ode45?解微分方程組的步驟通常包括:
1. 定義方程:首先,需要將問題轉化為一個或多個微分方程。
2. 編寫函數:在 MATLAB 中,你需要編寫一個函數來定義這些方程。這個函數將接受當前的狀態(比如位置和速度)和時間作為輸入,并返回狀態的導數(比如加速度)。
3. 調用 ode45:使用 `ode45` 函數,輸入你的方程函數、初始條件、時間跨度等參數。
4. 分析結果:ode45?將返回一個近似的數值解,你可以用它來進行進一步的分析或繪圖。
三、彈簧振子模型代碼實踐
有一個掛在天花板上的彈簧,下面掛著一個質量為
m的物體。如果把這個物體拉下來一點然后放手,它會開始上下振動,這就是一個彈簧振子系統。這個系統的運動可以通過一個二階微分方程來描述:
?
為了使用 ode45,我們需要將這個二階方程轉換為一階方程組。我們引入一個新的變量 v = dx/dt,表示物體的速度。那么加速度 d^2x/dt^2 就可以表示為 dv/dt。這個過程有點像狀態空間方程的改寫。現在我們有兩個方程:?
?現在,我們可以按照以下步驟使用 ode45:
1.定義方程,編寫函數:
function dxdt = spring_system(t, x)m = 1; % 質量 mk = 4; % 彈簧常數 kdxdt = [x(2); -k/m * x(1)]; % 返回速度和加速度
end?2.調用ode45:
% 從 t=0 到 t=10,初始位置為 1,初始速度為 0
[t, x] = ode45(@spring_system, [0, 10], [1, 0]); 3.分析結果:
plot(t, x(:,1), 'r', 'LineWidth', 2); % 繪制位置隨時間變化的圖
hold on;
plot(t, x(:,2), 'b', 'LineWidth', 2); % 繪制速度隨時間變化的圖
xlabel('Time');
ylabel('Displacement/Velocity');
legend('Displacement', 'Velocity');四、完整代碼?
下面給出完整代碼:
% 模擬參數
tspan = [0 10]; % 時間區間
x0 = [0.5; 0]; % 初始條件,假設初始位置為 0.5 m,初始速度為 0 m/s% 使用 ODE45 求解微分方程
[t, x] = ode45(@spring_system, tspan, x0); %x中接收到的是函數返回值的原函數位移和速度% 繪圖
figure;
plot(t, x(:,1), 'r', 'LineWidth', 2); % 繪制x隨時間變化的圖(位置)
hold on;
plot(t, x(:,2), 'b', 'LineWidth', 2); % 繪制x的導數隨時間變化的圖(速度)
xlabel('Time (s)');
ylabel('Displacement (m) / Velocity (m/s)');
legend('Displacement', 'Velocity');
title('Spring System Simulation');% 局部函數定義:定義微分方程系統
function dxdt = spring_system(t, x)m = 1; % 質量 mk = 4; % 彈簧常數 kdxdt = [x(2); -k/m * x(1)]; % 返回速度和加速度
end?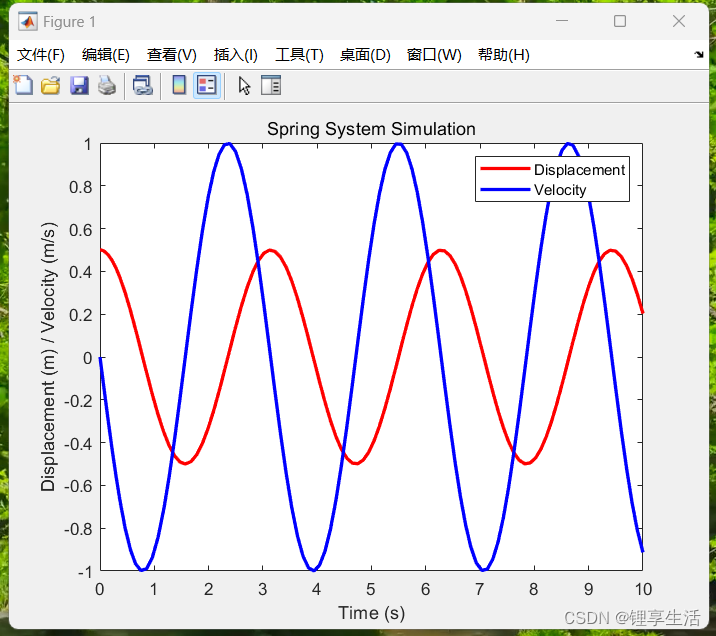






![[C++核心編程-06]----C++類和對象之對象模型和this指針](http://pic.xiahunao.cn/[C++核心編程-06]----C++類和對象之對象模型和this指針)

——數據要素:數據要素管理與數據管理)




)
)


)

