---

二叉搜索樹的概念

二叉搜索樹,它的左子樹的值比根的值小,右子樹的值比根的值大

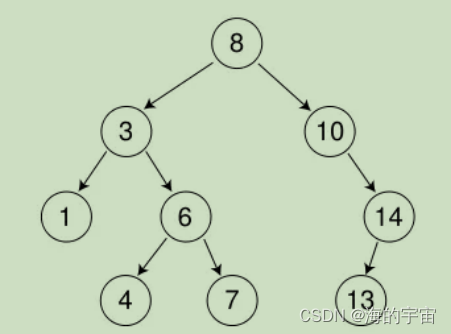
比如這一樹,根節點的值8比左子樹所有節點都大,比右子樹的所有節點都小.

二叉搜索樹的操作

二叉搜索樹的查找find

因為二叉樹有以上特性,所有使得它在搜索方面有極大的優勢.
比如我們要找值為7的節點在不在
1.我們從根節點開始找,因為7<根節點的值8,所有根節點在左子樹

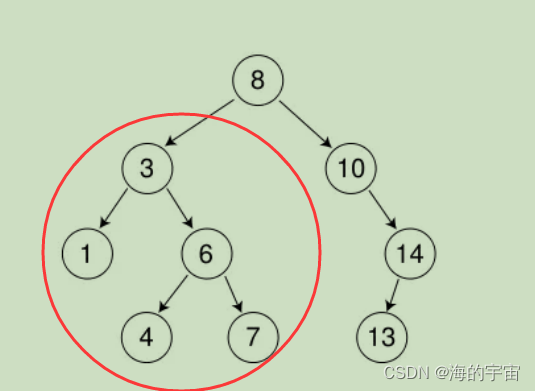
2.現在根節點的值為3<7,所有在3的右子樹中

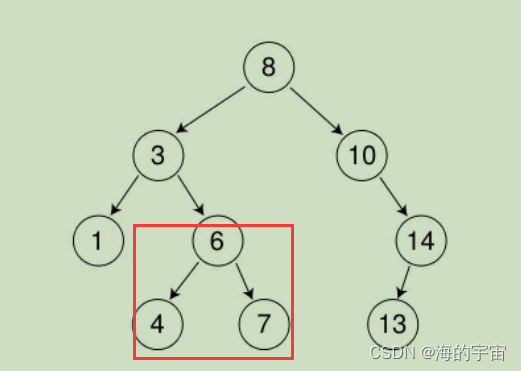
3.現在根節點的值為6<7,所有在6的右子樹中,剛好右子樹的節點為7.

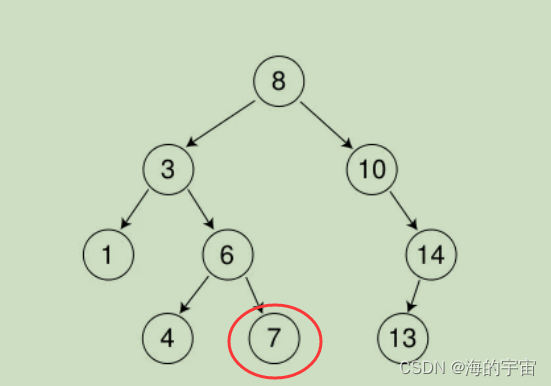
二叉搜索樹最多尋找高度次,如果走到空還沒有找到,說明這個值不存在

二叉搜索樹的模擬實現

構造節點

	template<class K>struct BSTreeNode{typedef BSTreeNode<K> Node;Node* _left;Node* _right;K _val;BSTreeNode(const K& val):_left(nullptr), _right(nullptr), _val(val){}};

_val里面存節點的值

insert

bool insert(const K& val)
{//a.樹為空,直接構造新節點賦值給根節點if (_root == nullptr){_root = new Node(val);return true;}Node* parent = nullptr;Node* cur = _root;//找到空的節點進行插入while (cur){if (cur->_val < val){parent = cur;cur = cur->_right;}else if (cur->_val > val){parent = cur;cur = cur->_left;}// 二叉搜索樹默認不允許重復else{return false;}}cur = new Node(val);if (parent->_val < val){parent->_right = cur;}else{parent->_left = cur;}return true;
}

插入有兩種情況
a.樹為空,直接構造新節點賦值給根節點
b.樹不為空,按照二叉樹的性質找到應該插入的空位置插入.
注意:
在b情況下,要找到新節點的位置,也要找到該節點的父親節點,這樣才能進行鏈接
假設要插入0節點,不光要找到0節點應該放的位置,還要找到0節點的父親1,將他們鏈接起來

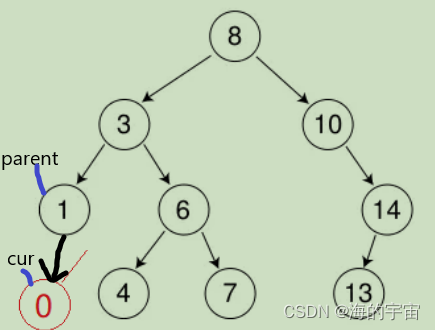
find

bool find(const K& val)
{Node* cur = _root;while (cur){if (cur->_val < val){cur = cur->_right;}else if (cur->_val > val){cur = cur->_left;}else{return true;}}return false;
}

按照二叉搜索樹的概念,比根大的往右走,比根小的往左走.
找到返回true,找不到返回false

erase(細節巨多,面試可能會考)

erase里面的細節很多,要細品.

刪除的節點有多種可能

a.葉子節點

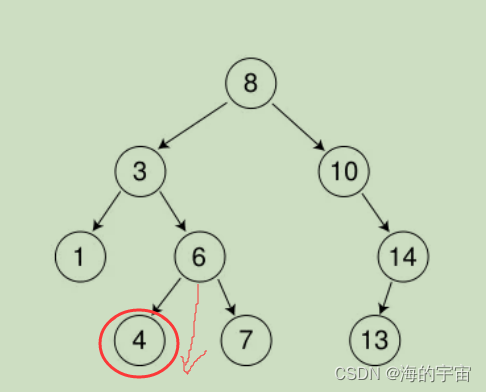
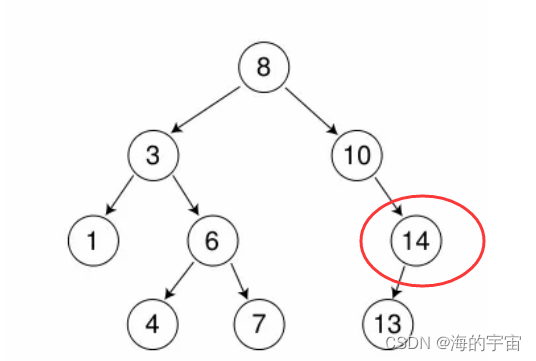
比如這棵樹我們要刪除4節點,就只需要找到4節點和它的父親節點6,讓父親節點6指向空,再刪除4節點.

b.有一個孩子

特殊情況
要刪除的是根節點,此時要更新新的根節點10.

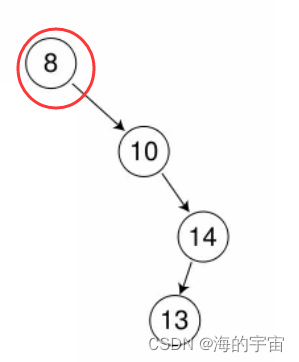
if (_root == cur)
{_root = cur->_right;delete cur;
}

左孩子

右為空,父親指向我的左
有一個左孩子,說明右子樹為空.
此時要讓父親指向3的左邊,此時不清楚是父親的左邊還是父親的右邊指向1節點

父親的左指向我的左

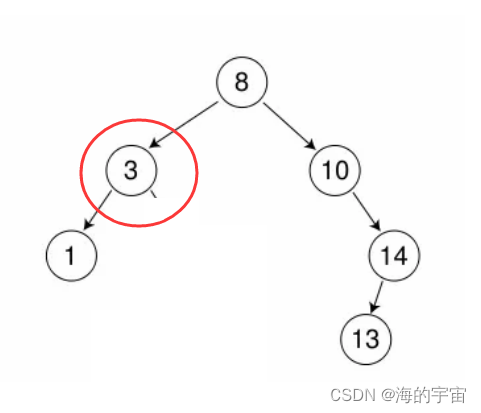
父親的右指向我的左

代碼實現

if (cur->_right == nullptr)
{//刪除頭節點if (_root == cur){_root = cur->_left;delete cur;}else{if (parent->_right == cur)parent->_right = cur->_left;elseparent->_left = cur->_left;delete cur;}
}

右孩子

左為空, 父親指向我的右

//左為空, 父親指向我的右
else if (cur->_left == nullptr)
{//刪除頭節點if (_root == cur){_root = cur->_right;delete cur;}else{if (parent->_right == cur)parent->_right = cur->_right;elseparent->_left = cur->_right;delete cur;}
}

右孩子的判斷和左孩子類似,方向反過來而已.

c.有兩個孩子

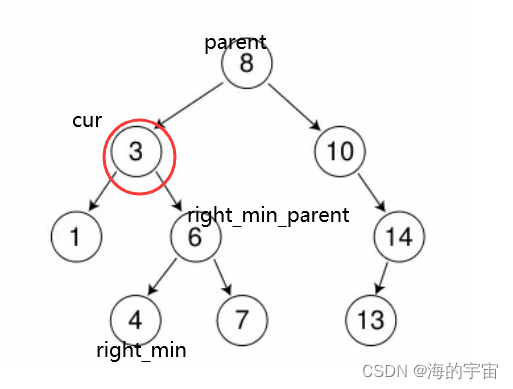
找到左邊的最大值或者右邊的最小值,與目標值進行替換.
這里以右邊的最小值為例.
我們尋找右邊的最小值時,同時要找它的父親節點,因為要對它的父親節點進行修改.
找到右邊的最小值為4,將4覆蓋到cur上面,再刪除right_min這個節點.

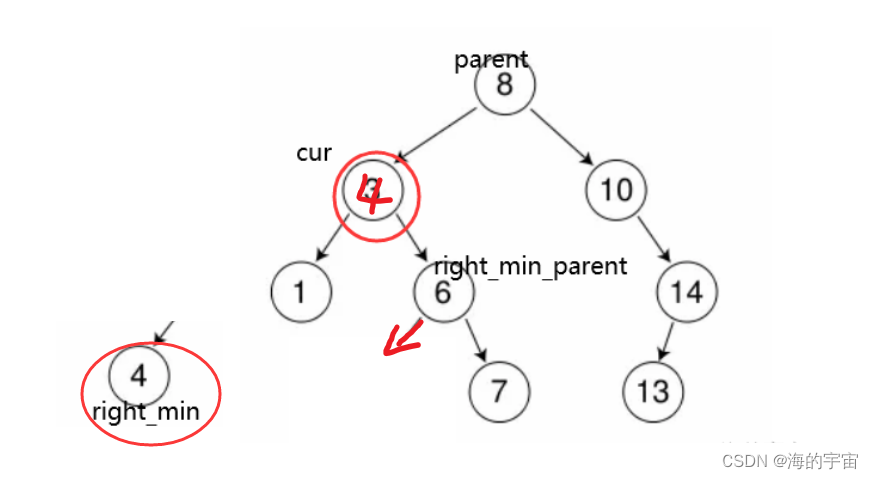
注意:

因為是尋找右子樹的最小值,所以這個最小值理論上應該沒有左子樹.
如果有左子樹,說明有更小的值.但是可能會有右子樹.
所有要讓right_min_parent左節點指向right_min的右節點.
這只是理論上,實際里面還有一個大坑

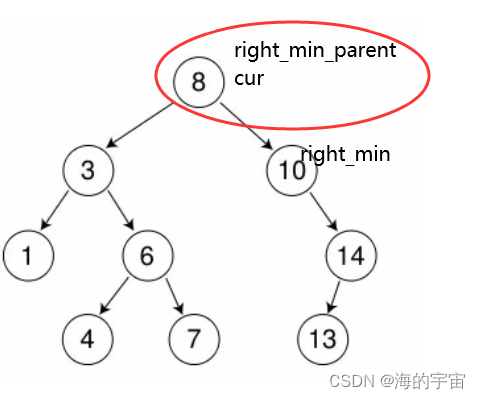
如果我們要刪除的節點:cur和right_min_parent 指向同一個地方時,此時應該讓right_min_parent 的右節點指向right_min的右節點.

//有兩個孩子:找到左邊的最大值或者右邊的最小值,與目標值進行替換//讓這個右最小節點的父親的左邊指向右最小的右邊,因為它此時最多只有右孩子
else
{Node* right_min_parent = cur;Node* right_min = cur->_right;while (right_min->_left){right_min_parent = right_min;right_min = right_min->_left;}cur->_val = right_min->_val;//右最小節點,有坑,是連續存放的有序值if (cur->_right == right_min)right_min_parent->_right = right_min->_right;elseright_min_parent->_left = right_min->_right;delete right_min;
}

erase代碼

bool erase(const K& val){Node* parent = _root;Node* cur = _root;//找到要刪除的目標值while (cur){if (cur->_val < val){parent = cur;cur = cur->_right;}else if (cur->_val > val){parent = cur;cur = cur->_left;}else{//只有一個孩子/葉子節點:讓父親節點指向子節點的右(nullptr)//右為空,父親指向我的左if (cur->_right == nullptr){//刪除頭節點if (_root == cur){_root = cur->_left;delete cur;}else{if (parent->_right == cur)parent->_right = cur->_left;elseparent->_left = cur->_left;delete cur;}}//左為空, 父親指向我的右else if (cur->_left == nullptr){//刪除頭節點if (_root == cur){_root = cur->_right;delete cur;}else{if (parent->_right == cur)parent->_right = cur->_right;elseparent->_left = cur->_right;delete cur;}}//有兩個孩子:找到左邊的最大值或者右邊的最小值,與目標值進行替換//讓這個右最小節點的父親的左邊指向右最小的右邊,因為它此時最多只有右孩子else{Node* right_min_parent = cur;Node* right_min = cur->_right;while (right_min->_left){right_min_parent = right_min;right_min = right_min->_left;}cur->_val = right_min->_val;//右最小節點,有坑,是連續存放的有序值if (cur->_right == right_min)right_min_parent->_right = right_min->_right;elseright_min_parent->_left = right_min->_right;delete right_min;}return true;}}return false;}

中序遍歷

		void MidOrder(){_MidOrder(_root);cout << endl;}private:void _MidOrder(const Node* root){if (root == nullptr){return;}_MidOrder(root->_left);std::cout << root->_val << " ";_MidOrder(root->_right);}

首先,中序的搜索方式是左子樹 根 右子樹.按照這個順序就能有序的取出搜索二叉樹里面的值了

為什么會有兩個函數?
因為函數的形參沒有this指針,沒法調用_root根節點,我們需要另外一個函數來傳_root根節點

二叉搜索樹的應用

k模型

k模型跟我們上面實現的一樣,只存儲一個值
比如:我們可以用這個功能查找到我們英文作文里面的拼寫錯誤的單詞.
我們可以把詞庫里面所有的英語單詞丟進這個二叉搜索樹,再遍歷整個作文,檢查每個單詞是否存在,不存在就報錯.

k模型模擬實現的總代碼

namespace shh1
{template<class K>struct BSTreeNode{typedef BSTreeNode<K> Node;Node* _left;Node* _right;K _val;BSTreeNode(const K& val):_left(nullptr), _right(nullptr), _val(val){}};//k模型template<class K>class BSTree{typedef BSTreeNode<K> Node;public:bool insert(const K& val){if (_root == nullptr){_root = new Node(val);return true;}Node* parent = nullptr;Node* cur = _root;//找到空的節點進行插入while (cur){if (cur->_val < val){parent = cur;cur = cur->_right;}else if (cur->_val > val){parent = cur;cur = cur->_left;}// 二叉搜索樹默認不允許重復else{return false;}}cur = new Node(val);if (parent->_val < val){parent->_right = cur;}else{parent->_left = cur;}return true;}bool erase(const K& val){Node* parent = _root;Node* cur = _root;//找到要刪除的目標值while (cur){if (cur->_val < val){parent = cur;cur = cur->_right;}else if (cur->_val > val){parent = cur;cur = cur->_left;}else{//只有一個孩子/葉子節點:讓父親節點指向子節點的右(nullptr)//右為空,父親指向我的左if (cur->_right == nullptr){//刪除頭節點if (_root == cur){_root = cur->_left;delete cur;}else{if (parent->_right == cur)parent->_right = cur->_left;elseparent->_left = cur->_left;delete cur;}}//左為空, 父親指向我的右else if (cur->_left == nullptr){//刪除頭節點if (_root == cur){_root = cur->_right;delete cur;}else{if (parent->_right == cur)parent->_right = cur->_right;elseparent->_left = cur->_right;delete cur;}}//有兩個孩子:找到左邊的最大值或者右邊的最小值,與目標值進行替換//讓這個右最小節點的父親的左邊指向右最小的右邊,因為它此時最多只有右孩子else{Node* right_min_parent = cur;Node* right_min = cur->_right;while (right_min->_left){right_min_parent = right_min;right_min = right_min->_left;}cur->_val = right_min->_val;//右最小節點,有坑,是連續存放的有序值if (cur->_right == right_min)right_min_parent->_right = right_min->_right;elseright_min_parent->_left = right_min->_right;delete right_min;}return true;}}return false;}bool find(const K& val){Node* cur = _root;while (cur){if (cur->_val < val){cur = cur->_right;}else if (cur->_val > val){cur = cur->_left;}else{return true;}}return false;}void MidOrder(){_MidOrder(_root);cout << endl;}private:void _MidOrder(const Node* root){if (root == nullptr){return;}_MidOrder(root->_left);std::cout << root->_val << " ";_MidOrder(root->_right);}private:Node* _root = nullptr;};void BST_Test1(){int a[] = { 6,5,1,4,7,2,3,8,9,11,55,68,-1 };BSTree<int> t;for (auto e : a){t.insert(e);}t.MidOrder();}void BST_Test2(){int a[] = { 8 };BSTree<int> t;for (auto e : a){t.insert(e);}t.MidOrder();for (auto e : a){t.erase(e);t.MidOrder();}}
}

k-value模型

每一個關鍵碼key，都有與之對應的值Value，即<Key, Value>的鍵值對。
這個在我們日常生活很常見,比如詞典的翻譯,我們在key里面存英語單詞,value里面存相對應的中文翻譯.
我們就可以通過輸入英文單詞得到其對應的中文翻譯.
下面稍作演示:

void TestBSTree(){BSTree<string, string> dict;dict.Insert("insert", "插入");dict.Insert("erase", "刪除");dict.Insert("left", "左邊");dict.Insert("string", "字符串");string str;while (cin >> str){auto ret = dict.Find(str);if (ret){cout << str << ":" << ret->_val << endl;}else{cout << "單詞拼寫錯誤" << endl;}}}

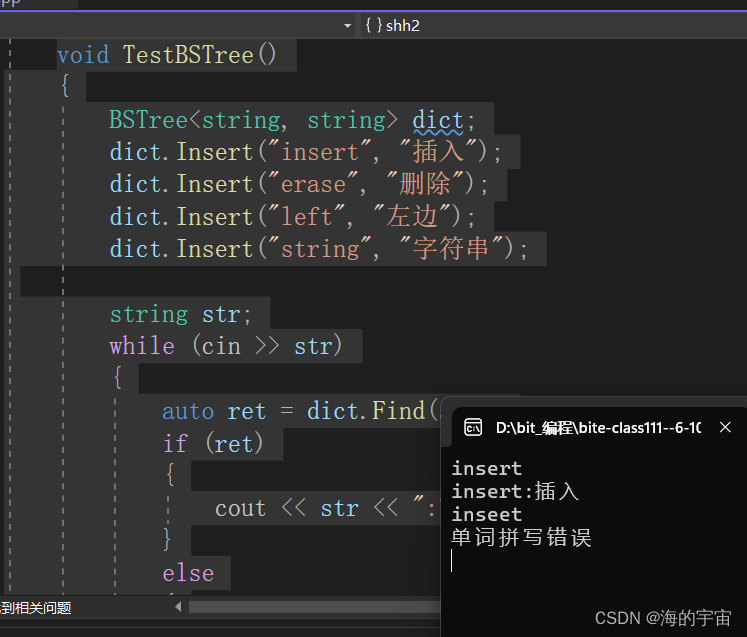
k-value模型模擬實現的總代碼

k-value模型的代碼和上面的key模型類似,我們只需要要添加新節點的時候再加一個值就行.

namespace shh2
{template<class K, class V>struct BSTreeNode{typedef BSTreeNode<K, V> Node;Node* _left;Node* _right;K _key;V _val;BSTreeNode(const K& key, const V& val):_left(nullptr), _right(nullptr), _key(key), _val(val){}};template<class K, class V>class BSTree{typedef BSTreeNode<K, V> Node;Node* _root = nullptr;public:bool Insert(const K& key, const V& val){//頭節點if (_root == nullptr){_root = new Node(key, val);return true;}Node* parent = _root;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{//已經插入過的return false;}}cur = new Node(key, val);if (parent->_key < key)parent->_right = cur;elseparent->_left = cur;return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return cur;}}return nullptr;}bool Erase(const K& key){Node* parent = _root;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{//葉子節點和只有一個孩子的一起處理//左為空,父親的左/右指向我的右if (cur->_left == nullptr){// 如果為根節點if (cur == _root){_root = cur->_right;delete cur;}else{if (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}delete cur;}}//右為空,父親的左/右指向我的左else if (cur->_right == nullptr){// 如果為根節點if (cur == _root){_root = cur->_left;delete cur;}else{if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}delete cur;}}//兩個孩子 找到cur左子樹的最大值替換else{Node* left_max_parent = cur;Node* left_max = cur->_left;while (left_max->_right){left_max_parent = left_max;left_max = left_max->_right;}swap(cur->_key, left_max->_key);if (left_max_parent->_left = left_max)left_max_parent->_left = left_max->_left;elseleft_max_parent->_right = left_max->_left;delete left_max;}return true;}}}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << ":" << root->_val << endl;_InOrder(root->_right);}void InOrder(){_InOrder(_root);}};void TestBSTree(){BSTree<string, string> dict;dict.Insert("insert", "插入");dict.Insert("erase", "刪除");dict.Insert("left", "左邊");dict.Insert("string", "字符串");string str;while (cin >> str){auto ret = dict.Find(str);if (ret){cout << str << ":" << ret->_val << endl;}else{cout << "單詞拼寫錯誤" << endl;}}}
};

二叉搜索樹的不足

當二叉搜索樹有序存入了一段值

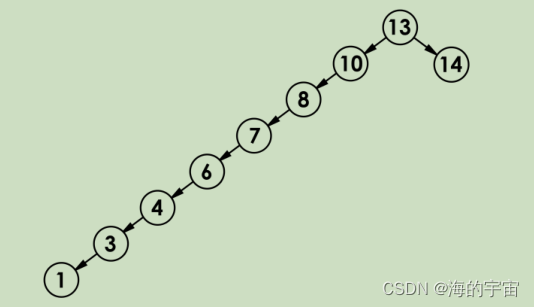
這棵樹會退化成單叉樹,因為插入,查找和刪除的時間復雜度都是高度次,
所以在這種情況下插入,查找和刪除的時間復雜度會接近于N.搜索二叉樹也就失去了它的優勢.

AVL樹和紅黑樹的出現

怎么解決這個問題呢,就要用到AVL和紅黑樹了.
在插入的時候,AVL樹會查看樹的高度是否平衡,
左子樹和右子樹的高度差不超過1.超過1會讓樹的幾個節點之間發生旋轉,最終這棵樹會變成這樣.

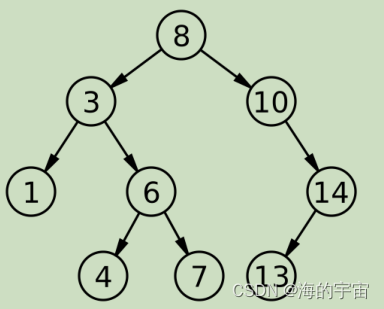
我們平時調用的容器map和set底層就是用AVL樹和紅黑樹生成的.

總結

二叉搜索樹的插入和查找不難,但是它的刪除細節很多,分類很細,一不留神容易掉坑里面,面試也經常會考.大家如果不懂的話,要多看幾遍.