標題什么是生成樹？

對于一張無向圖，由$n$個頂點和$n?1$條邊構成地聯通子圖，叫做這個無向圖 生成樹

最小生成樹就是指邊權之和最小的生成樹

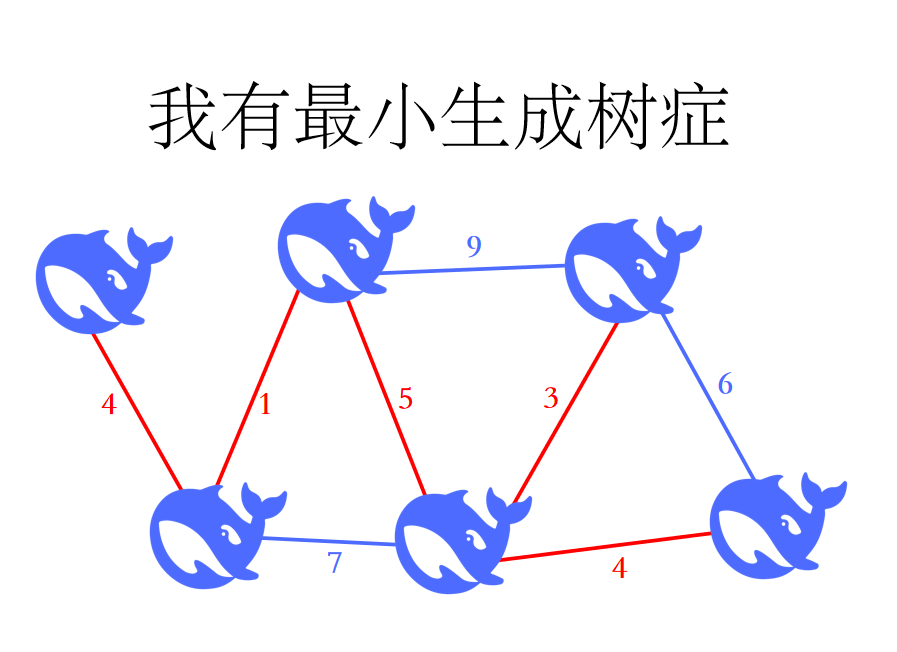
如何求最小生成樹？

Kruskal

介紹:

1. 存圖時只存每條邊地起點、終點，而不關注節點之間的聯通關系，所以不需要鏈式前向星或鄰接矩陣
2. 然后使用邊權排序，想像自己獲得了$n$個點，現在需要給這$n$個點連邊。
3. 循環遍歷存邊地數組，對于每條邊，取出它的兩個端點：$x$和$y$,同時使用并查集記錄點與點之間是否聯通。如果聯通，則證明該點之間已經存在最優的邊(因為權值更小的邊已經排到前面去了，會被優先考慮)。如果不聯通，就連上這兩條邊，使用并查集記錄。
4. 最后統計出該最小生成樹的所有邊的邊權之和

代碼實現

最小生成樹模板題目

#include<bits/stdc++.h>
using namespace std;
int read(){int s=0,fl=1;char w=getchar();while(w>'9'||w<'0'){if(w=='-')fl=-1;w=getchar();}while(w<='9'&&w>='0'){s=s*10+(w^48);w=getchar();}return fl*s;
}
void out(int x){if(x<0)putchar('-'),x=-x;if(x<10)putchar(x+'0');else out(x/10),putchar(x%10+'0');
}
struct ed{int v,x,y;
}mp[1000010];
int f[1000010],cnt;
bool cmp(ed x,ed y){return x.v<y.v;
}
int find(int x){if(f[x]!=x) f[x]=find(f[x]);return f[x];
}
int n,m,ans;
int main(){n=read();m=read();for(int i=1;i<=m;i++){mp[i].x=read();mp[i].y=read();mp[i].v=read();//存邊}sort(mp+1,mp+1+m,cmp);for(int i=1;i<=n;i++){f[i]=i;//初始化并查集}for(int i=1;i<=m;i++){int x=find(mp[i].x);int y=find(mp[i].y);if(x==y) continue;//如果最上層的祖先是一樣的，則證明已經聯通，跳過該條邊f[x]=y;//將兩條邊的祖先連在一起cnt++;ans+=mp[i].v;//統計和}cnt==n-1?printf("%d",ans):printf("orz");//判斷連上的節點數是否是整張圖的節點數，如果不是就證明原圖不連通，輸出orzreturn 0;
}

雙倍經驗

P1967 [NOIP 2013 提高組] 貨車運輸

由題意可得$A$國由$n$個點，$m$條邊構成，每條邊權重為$z$，貨車要從節點$x$走到節點$y$，每走一條邊，貨車的載重量不能超過當前邊的權值。
此題在想不到最小生成樹的情況下可以使用$Dijkstra$，要求貨車最大的載重量，肯定優先選擇邊權更大的邊通過，于是設$d[i]$表示從節點$x$到節點$i$的最大載重。判斷邏輯顯然可得：

if(new_dis>d[y]){d[y]=new_dis;

堆優化版$Dijkstra$時間復雜度是O_((V+E)logV) 但是這道題$V$=$1e4$,$E$=$5e4$,計算得最終為$8.4e4$,但是這只是單次$Dijkstra$，算上詢問次數，總時間約是$2.4e9$,一定超時
如果用離線處理，效率會高一些，但是還是無法通過此題

正解

使用最小生成樹和 最近公共祖先(lca) 解決
因為無論如何貨車走的路都一定是最大邊權的邊，然而生成樹的性質有一條就是能聯通所有節點，所以我們可以先對這張圖求 最大生成樹

然后對于每個詢問$x$和$y$，求出其最近公共祖先$l$,然后在求$lca$途中維護$w[i][j]$表示從節點$i$向上移動 2^j 層后的最大值。

因為求$lca$的過程是倍增進行的，所以總時間復雜度是$O(mlogm+nlogn+qlogn)$

#include<bits/stdc++.h>
using namespace std;
const int N=100010;
int read(){int s=0,fl=1;char w=getchar();while(w>'9'||w<'0'){if(w=='-')fl=-1;w=getchar();}while(w<='9'&&w>='0'){s=s*10+(w^48);w=getchar();}return fl*s;
}
void out(int x){if(x<0)putchar('-'),x=-x;if(x<10)putchar(x+'0');else out(x/10),putchar(x%10+'0');
}
int n,m,q;
int d[N],f[N],dep[N],fa[N][21];
int head[N],ne[N],to[N],v[N],tot,vis[N],w[N][21];
struct node{int x,y,v;
}mp[N];
bool cmp(node x,node y){return x.v>y.v;//求最大生成樹
}
int find(int x){if(f[x]!=x) f[x]=find(f[x]);return f[x];
}
void add(int x,int y,int w){to[++tot]=y;ne[tot]=head[x];head[x]=tot;v[tot]=w;
}
void dfs(int x){vis[x]=1;for(int i=head[x];i;i=ne[i]){int u=to[i];if(vis[u]){continue;}dep[u]=dep[x]+1;fa[u][0]=x;w[u][0]=v[i];dfs(u);}
}
void kru(){for(int i=1;i<=n;i++){f[i]=i;}sort(mp+1,mp+1+m,cmp);for(int i=1;i<=m;i++){int x=find(mp[i].x);int y=find(mp[i].y);if(x==y){continue;}f[x]=y;add(mp[i].x,mp[i].y,mp[i].v);add(mp[i].y,mp[i].x,mp[i].v);}
}
int lca(int x,int y){if(find(x)!=find(y)){return -1;}int ans=2e9;if(dep[x]<dep[y]){swap(x,y);}for(int k=20;k>=0;k--){if(dep[fa[x][k]]>=dep[y]){ans=min(ans,w[x][k]);x=fa[x][k];}}if(x==y) return ans;for(int k=20;k>=0;k--){if(fa[x][k]!=fa[y][k]){x=fa[x][k];y=fa[y][k];}}ans=min(ans,min(w[x][0],w[y][0]));return ans;
}
int main(){n=read();m=read();for(int i=1;i<=m;i++){int x=read();int y=read();int v=read();mp[i].x=x;mp[i].y=y;mp[i].v=v;}q=read();kru();for(int i=1;i<=n;i++){if(vis[i]==1) continue;dep[i]=1;dfs(i);fa[i][0]=i;w[i][0]=2e9;}for(int i=1;i<=20;i++){for(int j=1;j<=n;j++){fa[j][i]=fa[fa[j][i-1]][i-1];w[j][i]=min(w[j][i-1],w[fa[j][i-1]][i-1]);//預處理倍增表}}for(int i=1;i<=q;i++){int x=read();int y=read();out(lca(x,y));putchar('\n');}return 0;
}