PINN物理信息神經網絡多變量回歸預測，Matlab實現

前言

物理信息神經網絡（Physics-Informed Neural Networks, PINNs）是一種結合深度學習與物理定律的神經網絡方法，旨在解決涉及偏微分方程（PDEs）的問題。以下是對該問題的詳細解答：

物理信息神經網絡的定義與核心思想
物理信息神經網絡（PINNs）是一種將物理定律嵌入到神經網絡中的方法，通過將物理方程、邊界條件和初始條件作為約束條件，指導神經網絡的訓練過程。這種方法能夠利用已知的物理定律來增強模型的泛化能力，尤其在數據稀缺或數據質量較低的情況下具有顯著優勢。
PINNs的核心機制
? 物理約束的嵌入：PINNs通過將物理方程（如偏微分方程）和邊界條件嵌入到神經網絡的損失函數中，使模型在訓練過程中自動滿足物理約束。例如，損失函數通常包括物理殘差項和邊界條件的殘差項。

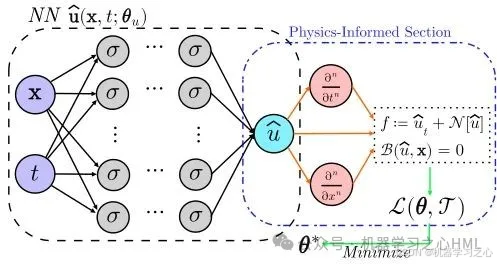
? 數據驅動與物理驅動的結合：PINNs可以同時利用數據和物理知識進行建模，即使在數據量較少的情況下也能獲得較好的預測結果。
? 靈活性與可擴展性：PINNs可以處理非線性問題、參數化問題以及多尺度問題，并且能夠處理復雜的物理系統，如流體力學、材料科學、地球物理學等。
PINNs的應用領域
PINNs在多個領域中得到了廣泛應用，包括但不限于：

? 流體力學與流體動力學：用于模擬流體流動、湍流、波傳播等。

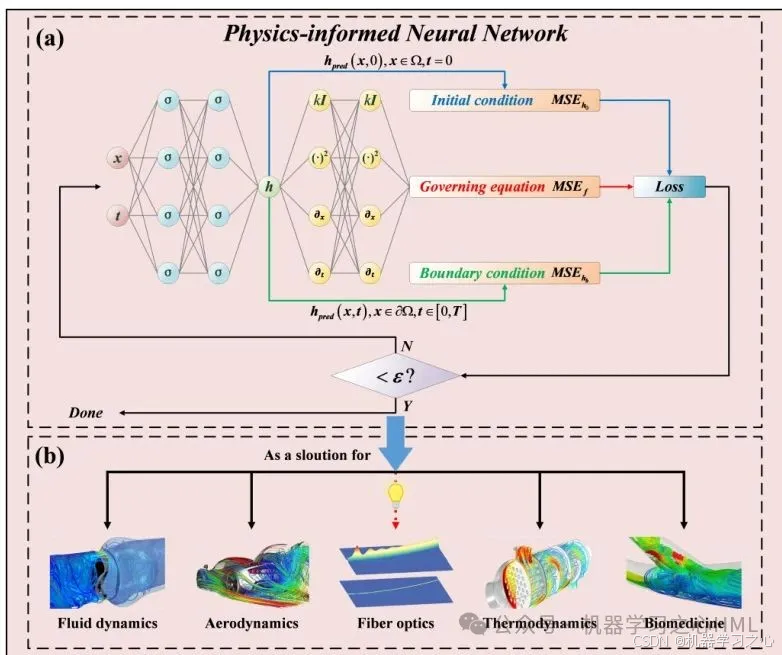
在這里插入圖片描述
材料科學與工程：用于模擬材料行為、微結構力學、異質材料等。
? 生物醫學與醫學成像：用于圖像重建、醫學成像、生物信號處理等。
? 能源與環境科學：用于模擬能源系統、氣候建模、環境動力學等。
4. PINNs的優勢與挑戰
? 優勢：
? 數據效率高：在數據稀缺的情況下，PINNs能夠通過物理約束提高模型的泛化能力。
? 可解釋性強：物理約束的引入增強了模型的可解釋性，有助于理解物理系統的復雜行為。
? 計算效率高：相比傳統數值方法（如有限元法），PINNs在某些情況下具有更高的計算效率。
? 挑戰：
? 優化難度：PINNs的訓練過程可能較為復雜，需要仔細調整超參數（如損失函數權重、學習率等）。
? 物理方程的表示：如何將復雜的物理方程和邊界條件準確地嵌入到神經網絡中仍是一個挑戰。

在這里插入圖片描述
5. PINNs的未來發展方向
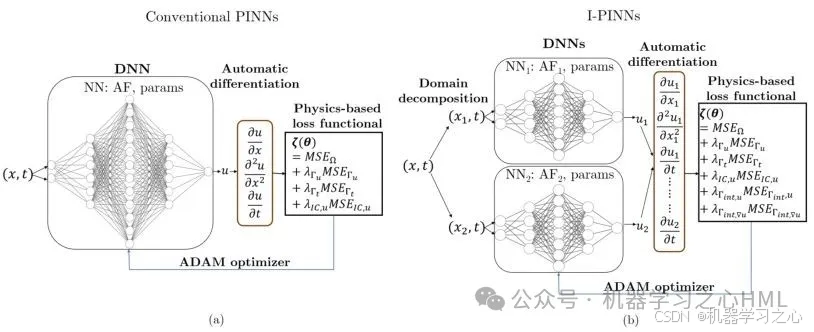
? 自適應物理信息神經網絡（SAPINNs）：通過引入自適應權重和動態調整物理約束，進一步提高模型的靈活性和適應性。
? 多尺度與多物理場耦合：發展能夠處理多尺度、多物理場耦合問題的PINNs模型。
? 與量子計算結合：探索PINNs與量子計算的結合，以解決更復雜的物理問題。
結論
物理信息神經網絡（PINNs）是一種將深度學習與物理定律相結合的創新方法，能夠有效解決涉及偏微分方程的復雜問題。通過將物理約束嵌入到神經網絡中，PINNs在數據稀缺、數據質量低或物理系統復雜的情況下具有顯著優勢。盡管在優化和物理方程表示方面仍存在挑戰，但PINNs在多個領域中展現出廣闊的應用前景。

代碼功能

MATLAB 代碼實現了一個物理信息神經網絡（Physics-Informed Neural Network, PINN），用于結合數據驅動與物理規律進行回歸預測。以下是詳細分析：

一、代碼功能概述

main.m
? 功能：主程序，完成數據導入、預處理、網絡構建、訓練、測試與可視化。
? 步驟：
? 導入數據并劃分訓練集和測試集；
? 數據歸一化；
? 構建全連接神經網絡（含3個隱藏層）；
? 使用包含物理約束的損失函數進行訓練；
? 評估模型性能（RMSE、R2、MAE、MAPE、MBE、MSE）；
? 繪制預測結果與誤差圖。
modelLoss.m
? 功能：自定義損失函數，計算數據損失與物理損失。
? 步驟：
? 計算數據擬合損失（MSE）；
? 在物理點上計算物理殘差（使用有限差分近似導數）；
? 組合得到總損失：總損失 = 數據損失 + λ * 物理損失；
? 返回梯度用于反向傳播。
二、邏輯關聯
? main.m 在訓練循環中調用 modelLoss 函數計算損失和梯度；
? modelLoss 利用 dlarray 和 dlgradient 實現自動微分，支持物理殘差的反向傳播；
? 物理點的生成和物理損失的引入是 PINN 的核心，使模型既擬合數據又遵守物理規律。
三、算法步驟
訓練流程（PINN）：
數據準備與劃分；
構建神經網絡；
在訓練數據點上計算數據損失；
在物理點上計算物理殘差（近似微分）；
組合損失并反向傳播更新網絡；
循環直至收斂。
四、技術路線
? 深度學習框架：使用 MATLAB 的 dlnetwork 和自動微分（DLToolbox）；
? 物理建模：通過有限差分法近似微分項，引入物理殘差；
? 優化算法：Adam 優化器；
? 評估指標：RMSE, R2, MAE, MAPE, MBE, MSE；
? 可視化：訓練過程損失曲線、預測對比圖、誤差分布、擬合圖。

在這里插入圖片描述
運行環境
? 軟件：MATLAB R2024b或更高版本（需 Deep Learning Toolbox）；
? 數據格式：Excel 文件（data.xlsx），最后一列為輸出。

數據集
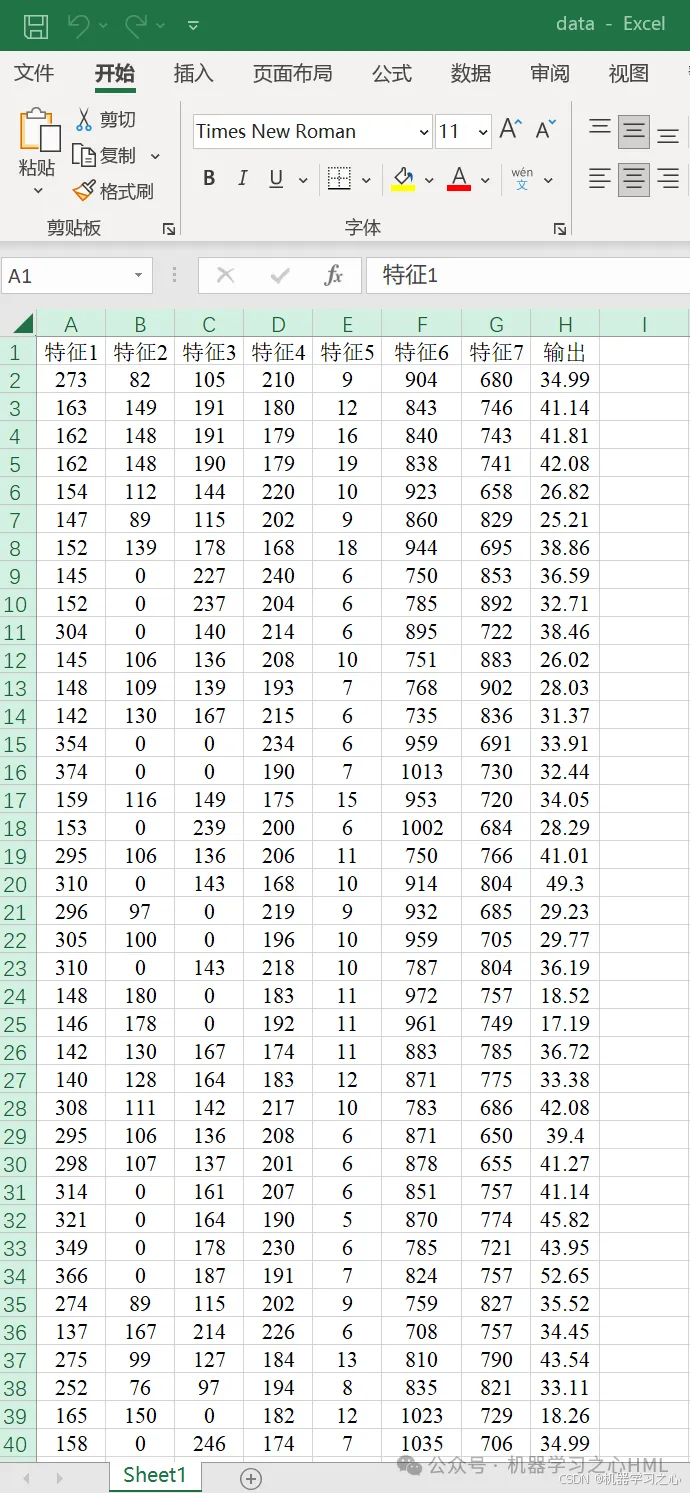
在這里插入圖片描述

運行效果

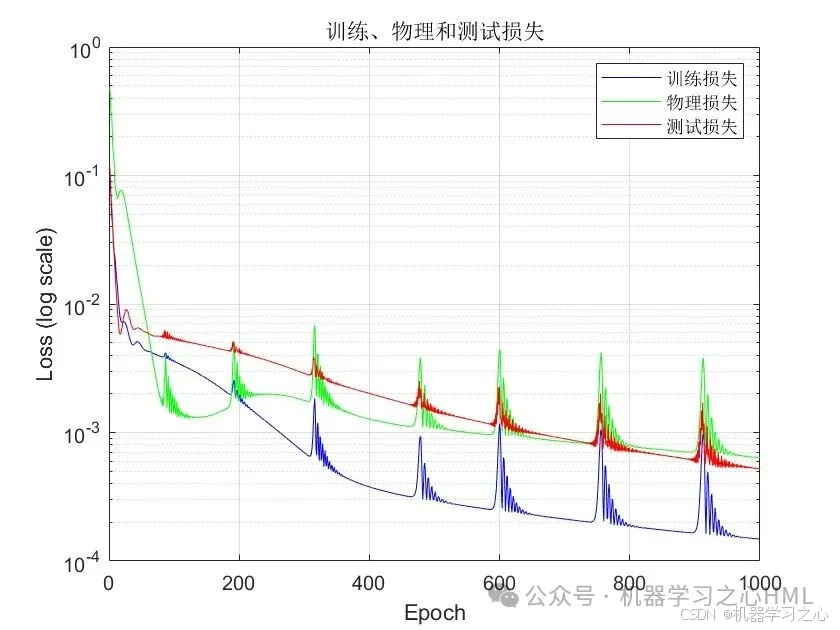
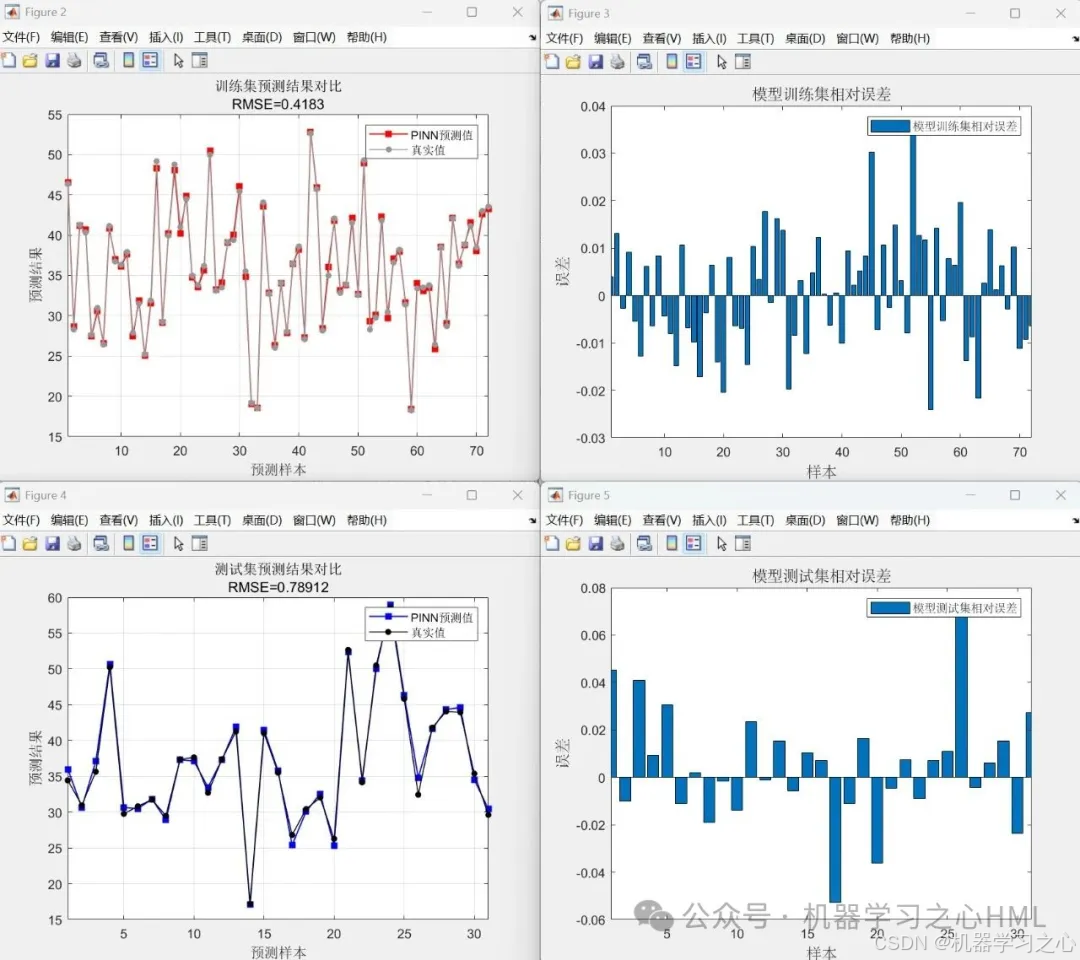
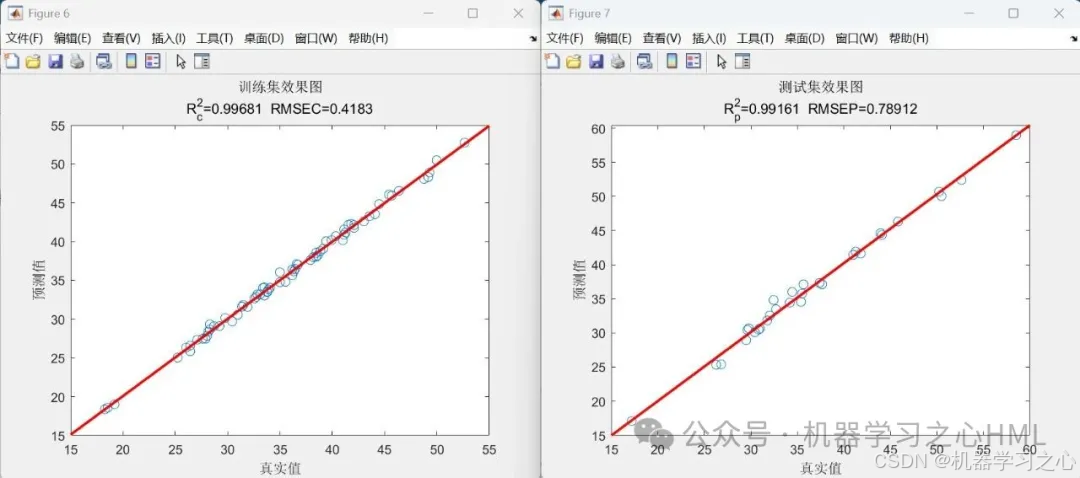
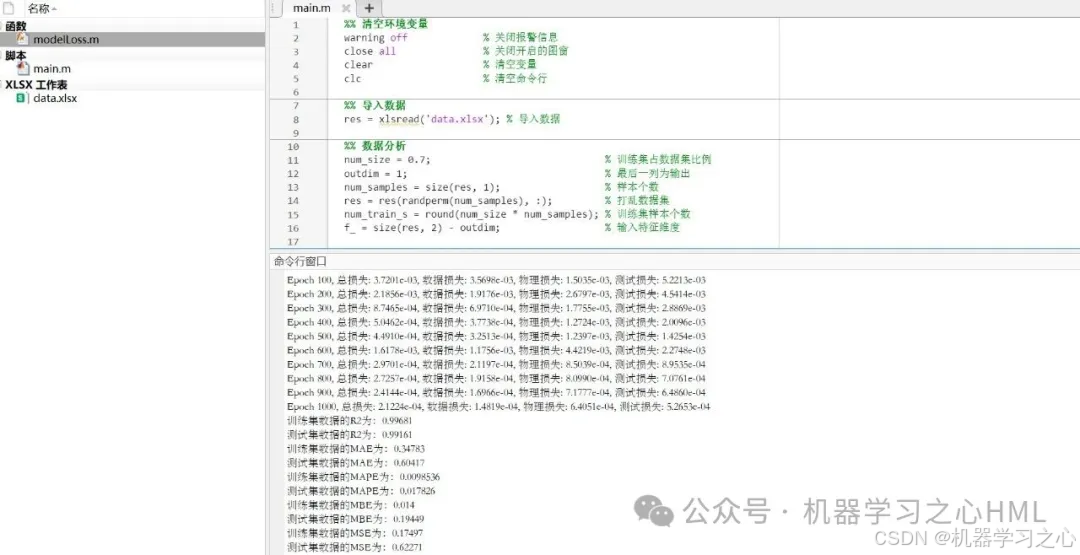
在這里插入圖片描述

PINN 核心特征在代碼中的體現

物理約束的引入 (modelLoss.m)
% 使用有限差分法近似計算導數

% 定義物理方程殘差（以常微分方程 du/dt + u = 0 為例）

% 計算物理損失
體現了PINN的核心：不僅擬合數據，還強制網絡滿足物理規律（微分方程）。

復合損失函數 (modelLoss.m)
% 組合總損失 = 數據損失 + λ * 物理損失
PINN的標志性特征——將物理知識作為正則化項加入損失函數。
物理點生成 (main.m)
% 生成物理點（用于計算物理殘差）
num_physics = 1000;
X_physics = rand(f_, num_physics);
PINN需要在物理域內采樣點來評估物理殘差，這些點不需要有標簽數據。
物理損失權重 (main.m)
lambda_phys = 0.1; % 物理損失項的權重
通過超參數λ平衡數據擬合與物理約束的重要性。
訓練過程中同時優化兩種損失 (main.m)
% 計算包含物理約束的損失和梯度
[totalLoss, dataLoss, physLoss, gradients] = dlfeval(@modelLoss, net, P_train_dl, T_train_dl, X_physics_dl, lambda_phys);
在每次訓練迭代中同時考慮數據誤差和物理一致性。

PINN在本代碼中的具體實現流程

數據準備：準備帶標簽的訓練數據
物理點采樣：在輸入域內隨機生成物理點
網絡前向傳播：同時計算數據點和物理點的輸出
物理殘差計算：使用有限差分法近似微分項
復合損失計算：結合數據誤差和物理殘差
反向傳播：同時優化數據擬合和物理一致性
循環訓練：不斷調整網絡參數以滿足雙重約束
核心思想
代碼完整實現了PINN的核心思想：

? ? 引入了物理方程作為軟約束
? ? 使用復合損失函數平衡數據擬合和物理一致性
? ? 在無標簽的物理點上評估物理殘差
? ? 通過超參數控制物理約束的強度
? ? 同時優化數據誤差和物理殘差
PINN與傳統神經網絡的根本區別——將物理先驗知識 explicitly 嵌入到學習過程中，而不僅僅依賴數據驅動。

部分源碼

.lineNode {font-size: 10pt; font-family: Menlo, Monaco, Consolas, "Courier New", monospace; font-style: normal; font-weight: normal; }
%% 清空環境變量
warning off             % 關閉報警信息
close all               % 關閉開啟的圖窗
clear                   % 清空變量
clc                     % 清空命令行
%% 導入數據
res = xlsread('data.xlsx'); % 導入數據
%% 數據分析
num_size = 0.7;                              % 訓練集占數據集比例
outdim = 1;                                  % 最后一列為輸出
num_samples = size(res, 1);                  % 樣本個數
res = res(randperm(num_samples), :);         % 打亂數據集
num_train_s = round(num_size * num_samples); % 訓練集樣本個數
f_ = size(res, 2) - outdim;                  % 輸入特征維度
%% 劃分訓練集和測試集
P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ + 1: end)';
M = size(P_train, 2);
P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + 1: end)';
N = size(P_test, 2);
%% 數據歸一化
[P_train, ps_input] = mapminmax(P_train, 0, 1);
P_test = mapminmax('apply', P_test, ps_input);
[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);
%% 轉換為dlarray格式
P_train_dl = dlarray(P_train, 'CB'); % 特征在行，樣本在列
T_train_dl = dlarray(t_train, 'CB');
P_test_dl = dlarray(P_test, 'CB');
T_test_dl = dlarray(t_test, 'CB');
%% 生成物理點（用于計算物理殘差）
% 假設輸入特征包含時間和空間信息，這里在[0,1]范圍內隨機生成物理點
num_physics = 1000; % 物理點數量
X_physics = rand(f_, num_physics); % 隨機生成物理點
X_physics_dl = dlarray(X_physics, 'CB'); % 轉換為dlarray
%% 創建PINN模型
layers = [featureInputLayer(f_, 'Name', 'input')fullyConnectedLayer(64, 'Name', 'fc1')