When and where soil dryness matters to ecosystem photosynthesis
來自 <When and where soil dryness matters to ecosystem photosynthesis | Nature Plants>
## Abstract:
- Background: Projected increases in the intensity and frequency of droughts in the twenty-first century are expected to cause a substantial negative impact on terrestrial gross primary productivity (GPP). Yet, the relative role of soil water supply (indicated by soil moisture) and atmospheric water demand (indicated by vapour pressure deficit, VPD) on GPP remains debated, primarily due to their strong covariations, the presence of confounding factors and unresolved causal relationships among the interconnected hydrometeorological drivers of GPP.
- How this paper solved this question: Here using a causality-guided explainable artificial intelligence framework, we show that soil moisture is the dominant regulator of water stress, surpassing the role of VPD, when and where soil water supply limits ecosystem functions.
- Temporally, use in situ flux tower data to demonstrate that sm dominates the GPP response during periods of insufficient soil water supply. Spatially, assess the global spatial patterns of satellite sun-induced chlorophyll fluorescence (a proxy for GPP) in water-limited regions and demonstrate that they are mostly dominated by soil moisture.
- Conversely, VPD plays a greater role in controlling the temporal and spatial variations in GPP than sm when and where sm is not limited.
(Essentially, this is because soil moisture can regulate VPD.)
## Intro:
- Terrestrial ecosystems offset approximately one-third of fossil fuel carbon dioxide (CO2) emissions, and this capacity depends on photosynthesis (indicated by the gross primary productivity, GPP).
- On the one hand, water supply from soil moisture (SM), as quantified by volumetric soil water content (VWC), can determine the accessible water for plant growth and function2. On the other hand, the water demand by the atmosphere, as quantified by vapour pressure deficit (VPD), determines the diffusion of water vapour from plants to the atmosphere, and under conditions of intensified atmospheric dryness, stomata on leaves tend to close to avoid excessive water loss.
- In addition, under conditions of low water availability, SM and VPD are highly (anti)correlated through land–atmosphere coupling.

Disentangling their impacts on GPP is challenging for several reasons:
first, SM and VPD often show strong covariations, particularly under water-limited conditions
second, there are confounding effects from other hydrometeorological drivers of GPP, particularly incoming shortwave radiation (SW) and air temperature (TA);
third, a less acknowledged aspect is that the causal relationships among GPP drivers vary notably between energy- versus water-limited conditions,
## Results:
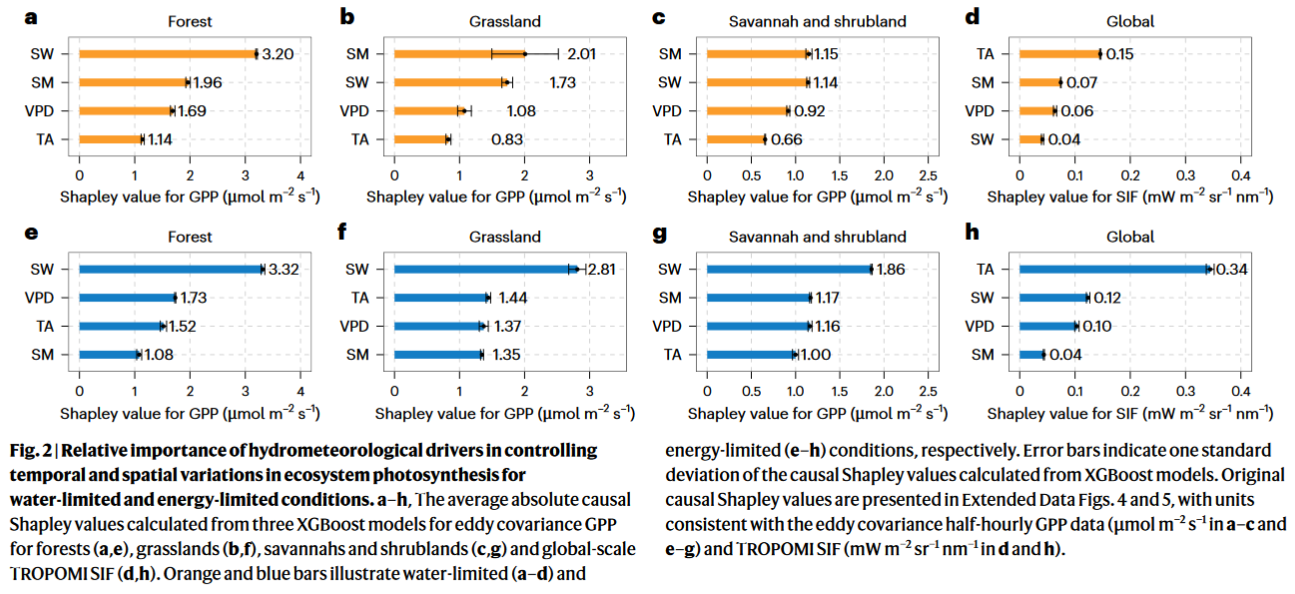
A framework for quantifying SM and VPD impacts on GPP
use an XAI framework guided by causal chain graphs to disentangle the relative roles of SM and VPD in driving the temporal and spatial variations in GPP.
- First, given the distinct causal structures between energy- and water-limited conditions (Fig. 1a,b), we identify these two regimes in our datasets over both time and space.
- Second, we characterized the complex nonlinear dependency of GPP on its hydrometeorological drivers using Extreme Gradient Boosting (XGBoost) models38 across both water- and energy-limited conditions in time and space. used observed and reanalysis data of SW, TA, VPD and SM
Third, we used an approach called the causal Shapley value40, which incorporates causal relationships among GPP drivers based on Pearl’s causal inference do-calculus41, to interpret the XGBoost models for disentangling the respective effects of VPD and SM on GPP.

Causal Shapley values
Compared to other attribution methods, the Shapley value ensures a fair distribution in the sense that it can be proven to be the only solution that simultaneously satisfies the four favourable axioms (efficiency, additivity, symmetry and null player)75. Here the ‘total gain’ is the observed GPP or SIF, and players are their drivers (that is, SW, TA, VPD and SM). For an M-player game, we assume that there is a function v(S) that maps the gain of |S| players to a real number, where the coalition S??= {1,...,M } consists of a subset of players (j). Thus, the Shapley value (φ) of player j, that is, the weighted averages of marginal contributions of j, can be calculated as follows
)
)

)




)
)


來控制電腦(版本1))






