【題目鏈接】
35. 搜索插入位置
【題目描述】

【題解】
通過題目可以知道這是一道經典的二分查找的題目，對于二分查找的題目，根據需要查找的兩個邊界點，分為兩個不同的模板，如下圖所示。

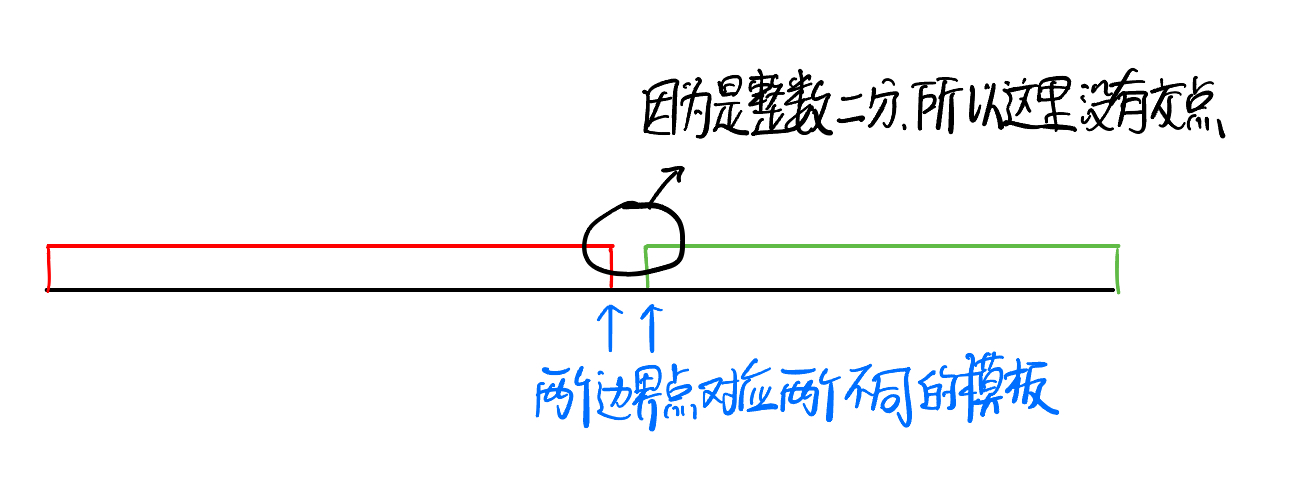
這道題要求在數組中查找目標值并返回其索引，若目標值不存在，則返回它按順序插入的位置。因此，它適合使用綠色邊界點對應的二分查找模板。
該模板適用于查找最小滿足條件的值的場景，常用于定位滿足特定條件的最小值或區間的左邊界。其核心邏輯是通過不斷收縮右邊界，最終定位到符合條件的最小值。

其模板如下：

bool check(int x) {/* ... */} // 檢查x是否滿足某種性質int bsearch_2(int l, int r)
{while (l < r){int mid = l + r >> 1;if (check(mid)) r = mid;else l = mid + 1;}return l;
}

【AC代碼】

class Solution {
public:int searchInsert(vector<int>& nums, int target) {int l = 0, r = nums.size();while(l < r) {int mid = l + r >> 1;if(nums[mid] >= target)r = mid;elsel = mid + 1;}return l;}
};

【思考】
1.能否使用紅色邊界點對應的模板呢？
這道題同樣可以用紅色邊界點對應的模板來解答，只是需要先將問題轉化為尋找最后一個小于目標值的元素位置，再通過推導得出插入位置。
該模板的核心是定位最后一個滿足條件的位置（即右邊界），而原問題實際需要的是第一個大于等于目標值的位置（即左邊界）。兩者的轉化邏輯很明確：插入位置 = 最后一個小于目標值的位置 + 1，而尋找最后一個小于目標值的位置恰好是紅色邊界點模板的典型應用場景。

其模板如下：

bool check(int x) {/* ... */} // 檢查x是否滿足某種性質int bsearch_1(int l, int r)
{while (l < r){int mid = l + r + 1 >> 1;if (check(mid)) l = mid;else r = mid - 1;}return l;
}

【AC代碼】

class Solution {
public:int searchInsert(vector<int>& nums, int target) {int l = 0, r = nums.size() - 1; while (l < r) {int mid = (l + r + 1) / 2; if (nums[mid] < target) { l = mid;} else {                  r = mid - 1;}}// 循環結束后，l是最后一個可能<target的位置，需判斷是否真的滿足if (nums[l] < target) {return l + 1; // 存在<target的元素，插入位置為l+1} else {return l;     // 所有元素≥target，插入位置為l（即第一個≥target的位置）}}
};

2.模板的兩個邊界l和r如何確定？
在ac之前，我卡在了一個地方，r一直取的值是r = nums.size() - 1，這導致在測試樣例時，示例1和示例2都可以通過，但輸入3確報了錯。通過調試輸出排查后發現，問題的根源在于邊界值的設置。
當r = nums.size() - 1時，示例1：
$l=0,r=3,mid=1,nums[mid]=3,3<target,l=mid+1=1+1=2;$
$l=2,r=3,mid=2,nums[mid]=5,5\ge 5,r=2;$
$l=2,r=2,$退出循環,返回l=2,答案正確。
當r = nums.size() - 1時，示例2：
$l=0,r=3,mid=1,nums[mid]=3,3＞target,r=1;$
$l=0,r=1,mid=0,nums[mid]=1,1＜target,l=mid+1=0+1=1;$
$l=1,r=1,$退出循環,返回l=1,答案正確。
當r = nums.size() - 1時，示例3：
$l=0,r=3,mid=1,nums[mid]=3,3＜target,l=mid+1=1+1=2;$
$l=2,r=3,mid=2,nums[mid]=5,5＜target,l=mid+1=2+1=3;$
$l=3,r=3,$退出循環,返回l=3,答案錯誤。
通過上述分析可以發現，r = nums.size()的設置確保了搜索區間覆蓋所有可能的插入位置，而r = nums.size() - 1會漏掉插入到數組末尾的情況，導致部分測試用例失敗。
二分查找的核心是明確搜索區間的定義，并確保區間覆蓋所有可能的解。