例題1：

704. 二分查找 - 力扣（LeetCode）

算法原理：（二分）

通過遍歷也可以通過，但是二分更優且數據量越大越能體現。

二分思路：

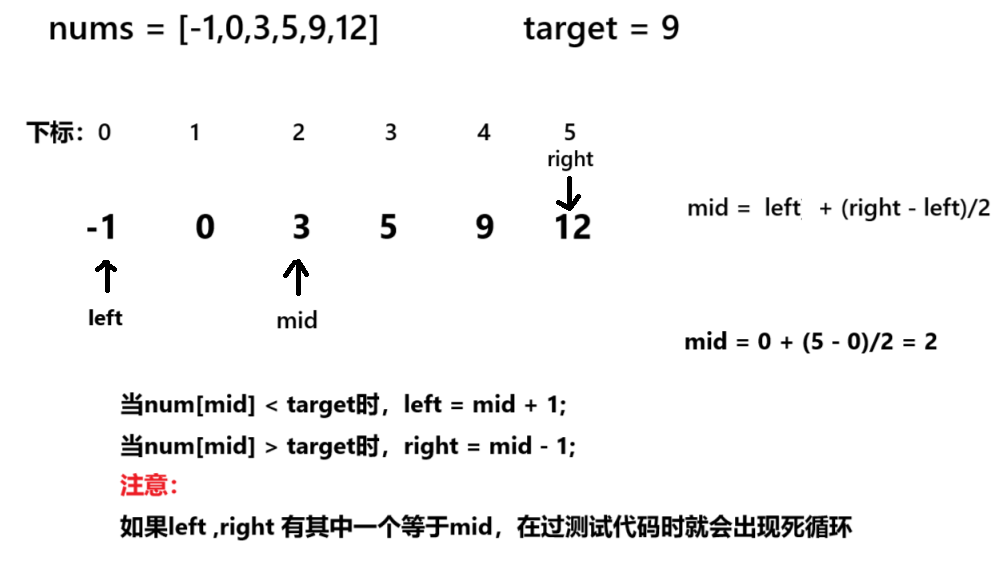
1.mid1 = ?(left + right)/2 與?mid2 = right +?(right - left)/2區別。

如果不考慮數據范圍：?(left + right)/2? =?right +?(right - left)/2，但越界就不一樣了。

mid1 = ?(left + right)/2?：可能越界

mid2 = left+?(right - left)/2 : 可以防止越界

2.mid1 = (right +?left)/2 與?mid2 = (right +?left + 1)/2區別。

(right +?left)/2? ： 向下取整

(right +?left + 1)/2 ：向上取整

舉個例子： right = 3,left = 4,(right +?left)/2? = 3,(right +?left + 1)/2 = 4;

? ? ? ? ? ? ? ? ? ?right = 2,left = 4,(right +?left)/2? = 3,(right +?left + 1)/2 = 3;

這里不會嚴格用數學方式去證明，那樣太花時間了，感興趣的話網上搜搜，我們直接給出結論，當right +?left 結果為偶數時，mid1 與 mid2 是沒有區別的，但結果為奇數時就會相差1，不要小看了這一點區別，不注意這里，就很有可能寫出死循環，具體我們在下面例題里體現。

這里不能通過調整上下取整的方式來避免死循環。但是可以通過增加一行代碼來弄

(? ? ? ?if(left == right && nums[left] != target) break;? ? ? )

代碼：

//暴力可以過😯public int search(int[] nums, int target) {int n = nums.length;for(int i = 0;i < n;i++){if(nums[i] > target){break;}if(nums[i] == target) return i;}return -1;}

     //二分public int search(int[] nums, int target) {int left = 0;int right = nums.length - 1;while(left <= right){int mid = left + (right - left)/2;if(nums[mid] < target){left = mid+1;}else if(nums[mid] ==target){return mid;}else {right = mid-1;}}return -1;}

//二分，調整后public int search(int[] nums, int target) {int left = 0;int right = nums.length - 1;while(left <= right){int mid = left + (right - left)/2;if(nums[mid] < target){left = mid+1;}else if(nums[mid] ==target){return mid;}else {right = mid;}if(left == right && nums[left] != target) break; }return -1;}

?

通過上面兩幅幅圖我們就可以感受到上，下取整差1，如果調整不好便會出現死循環。這里只列舉了向下取整，避免死循環情況。還有一種是向上取整，避免死循環情況。（再往下的例題就不會，所這么多了。）?

如下例題都是可以利用二分解決的，這里就提一點，二分的使用場景并不一定非要整個序列有序，而是依據你的需求，巧妙的去使用它。

例題2：

34. 在排序數組中查找元素的第一個和最后一個位置 - 力扣（LeetCode）

例題3：

162. 尋找峰值 - 力扣（LeetCode）

例題4：

153. 尋找旋轉排序數組中的最小值 - 力扣（LeetCode）