機器學習 —— 決策樹(Decision Tree)詳細介紹
決策樹是一種直觀且易于解釋的監督學習算法,廣泛應用于分類和回歸任務。它通過模擬人類決策過程,將復雜問題拆解為一系列簡單的判斷規則,最終形成類似 “樹” 狀的結構。以下從基礎概念、原理、算法類型、優缺點及應用場景等方面展開詳細介紹。
一、決策樹的基礎概念
1. 核心定義
決策樹是一種基于樹狀結構進行決策的模型,每個節點代表對某個特征的判斷,每條分支代表該判斷的可能結果,葉子節點則代表最終的決策結果(分類任務中為類別,回歸任務中為數值)。
2. 基本結構
- 根節點(Root Node):樹的起點,包含所有樣本數據,是第一個特征判斷的起點。
- 內部節點(Internal Node):表示對某個特征的判斷條件(如 “年齡是否> 30 歲”),每個內部節點會根據特征值分裂為多個子節點。
- 分支(Branch):連接節點的線段,代表特征判斷的結果(如 “是” 或 “否”)。
- 葉子節點(Leaf Node):樹的終點,輸出最終的預測結果(分類任務中為類別標簽,回歸任務中為預測值)。
示例:用決策樹判斷 “是否購買電腦”
根節點:收入水平(高 / 中 / 低)→ 內部節點:年齡(<30/30-40/>40)→ 葉子節點:購買 / 不購買。
二、決策樹的工作原理
決策樹的核心是如何選擇特征進行節點分裂,目標是通過分裂使子節點的 “純度” 更高(即子節點中的樣本盡可能屬于同一類別或數值更集中)。具體流程如下:
1. 特征選擇:如何分裂節點?
特征選擇的關鍵是通過不純度指標衡量分裂效果,常用指標包括:
(1)信息增益(Information Gain)—— ID3 算法
基于熵(Entropy)?計算,熵衡量樣本集合的混亂程度,熵值越低,純度越高。
- 熵的計算公式(針對分類任務):
對于樣本集合D,若有k個類別,每個類別占比為pi?,則熵為:
![]()
信息增益:分裂后子節點的熵與父節點熵的差值,即:
![]()
其中A為特征,Dv?為特征A取第v個值的子樣本集,信息增益越大,特征越優。
(2)信息增益率(Gain Ratio)—— C4.5 算法
解決信息增益偏向多值特征的問題(如 “身份證號” 這類特征分裂后熵極低,但無實際意義)。
信息增益率 = 信息增益 / 特征自身的熵(分裂信息)。
(3)基尼指數(Gini Index)—— CART 算法
衡量從樣本中隨機抽取兩個樣本,類別不同的概率,基尼指數越低,純度越高。
計算公式:
![]()
CART 算法通過最小化基尼指數選擇特征。
(4)均方誤差(MSE)—— 回歸樹
針對回歸任務,用子節點樣本的均方誤差衡量分裂效果,MSE 越小越好:
![]()
其中yˉ?為子節點樣本的均值。
2. 樹的構建過程
- 從根節點開始,計算所有特征的不純度指標(如信息增益)。
- 選擇最優特征進行分裂,將樣本分配到子節點。
- 對每個子節點重復步驟 1-2,直到滿足停止條件:
- 子節點樣本全部屬于同一類別(分類)或數值方差小于閾值(回歸)。
- 節點樣本數小于最小分裂閾值。
- 樹的深度達到預設最大值。
3. 剪枝:防止過擬合
決策樹若完全生長可能導致過擬合(對訓練數據擬合過好,泛化能力差),需通過剪枝優化:
- 預剪枝(Pre-pruning):在樹構建過程中提前停止分裂(如限制深度、最小樣本數)。
- 后剪枝(Post-pruning):先構建完整樹,再移除對泛化能力無幫助的分支(如通過交叉驗證判斷分支是否保留)。
三、常見決策樹算法對比
| 算法 | 任務類型 | 特征選擇指標 | 樹結構 | 優勢 | 缺點 |
|---|---|---|---|---|---|
| ID3 | 分類 | 信息增益 | 多叉樹 | 簡單直觀 | 不支持連續特征,易過擬合 |
| C4.5 | 分類 | 信息增益率 | 多叉樹 | 支持連續特征、缺失值處理 | 計算復雜,不支持回歸 |
| CART | 分類 / 回歸 | 基尼指數(分類)、MSE(回歸) | 二叉樹 | 可處理分類和回歸,效率高 | 對不平衡數據敏感 |
四、決策樹的優缺點
優點
- 可解釋性強:樹結構直觀,能清晰展示決策規則(如 “若年齡> 30 且收入高,則購買”)。
- 無需特征預處理:對特征縮放、歸一化不敏感,可直接處理類別型和數值型特征。
- 訓練效率高:基于貪心算法,計算復雜度較低(尤其 CART 樹)。
- 抗噪聲能力較強:通過剪枝可減少噪聲影響。
缺點
- 易過擬合:未剪枝的樹可能過度擬合訓練數據,泛化能力差。
- 對樣本敏感:訓練數據微小變化可能導致樹結構大幅改變(穩定性差)。
- 偏向高維特征:信息增益等指標可能優先選擇多值特征。
- 難以處理非線性關系:單個決策樹對復雜數據的擬合能力有限(可通過集成學習彌補)。
五、決策樹的擴展:集成學習
為解決單個決策樹的局限性,衍生出集成學習方法,通過組合多個決策樹提升性能:
- 隨機森林(Random Forest):多個決策樹的投票 / 平均,通過隨機采樣樣本和特征降低方差。
- 梯度提升樹(GBDT):迭代生成決策樹,每個樹修正前序樹的誤差,提升精度。
- XGBoost/LightGBM:優化的 GBDT 實現,效率和精度更優,廣泛用于競賽和工業界。
六、應用場景
決策樹因其易解釋性和實用性,在多個領域廣泛應用:
- 金融風控:信用評分(如 “收入> 5 萬且無逾期,則貸款批準”)。
- 醫療診斷:疾病判斷(根據癥狀特征逐步排查病因)。
- 客戶分類:用戶畫像與行為預測(如 “高活躍度且消費頻繁的用戶為優質客戶”)。
- 工業質檢:通過特征判斷產品是否合格。
- 回歸預測:房價預測、銷量預測等(回歸樹)。
總結
決策樹是一種簡單高效的監督學習算法,核心是通過不純度指標選擇特征分裂節點,結合剪枝優化避免過擬合。盡管存在穩定性差等局限,但通過集成學習(如隨機森林、GBDT)可顯著提升性能,使其成為工業界和學術界的重要工具。理解決策樹的原理是掌握集成學習的基礎,也是機器學習入門的核心知識點之一。
用一個簡單案例說明ID3的計算方法
數據如圖所示
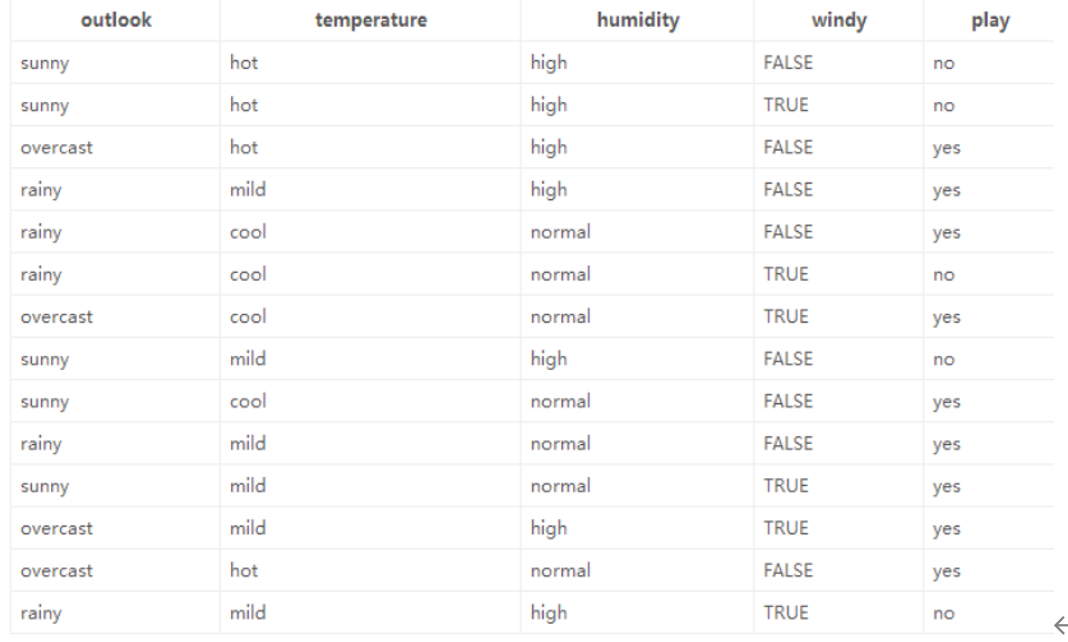
以下是使用?ID3 算法?構建決策樹的詳細計算過程,基于你提供的天氣數據集(判斷是否適合戶外運動?play),步驟如下:
1. 數據集與目標
- 數據集:包含 14 條樣本,特征為?
outlook(天氣)、temperature(溫度)、humidity(濕度)、windy(是否有風),標簽為?play(是否適合運動,yes/no)。 - 目標:用 ID3 算法選擇特征、構建決策樹,實現對?
play?的分類。
2. ID3 核心思想:用?信息增益(Information Gain)?選擇最優特征
信息增益公式:
![]()
- H(D):數據集?D?的?經驗熵(衡量標簽不確定性)。
- H(Dv?):特征?A?取值為?v?時子集?Dv??的經驗熵。
- 信息增益越大,特征對分類結果的 “區分度” 越高,優先選它做決策節點。
3. 計算步驟
步驟 1:計算數據集?D?的經驗熵?H(D)
標簽?play?的分布:
yes:9 條(索引 2,3,4,6,8,9,10,11,12)no:5 條(索引 0,1,7,13,5)
經驗熵公式:
![]()
其中?pk??是標簽?k?的占比。
代入計算:

步驟 2:對每個特征,計算信息增益?IG(D,A)
特征 1:outlook(取值:sunny、overcast、rainy)
子集劃分:
sunny(D1):5 條(索引 0,1,7,8,10)→?play?分布:no(3 條)、yes(2 條)overcast(D2):4 條(索引 2,6,11,12)→?play?分布:yes(4 條)、no(0 條)rainy(D3):5 條(索引 3,4,5,9,13)→?play?分布:yes(3 條)、no(2 條)
計算各子集的經驗熵:
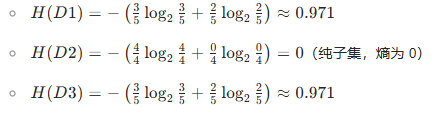
信息增益?IG(D,outlook):
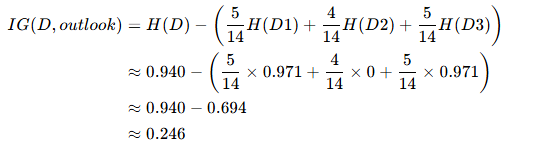
特征 2:temperature(取值:hot、mild、cool)
子集劃分:
hot(D1):4 條(索引 0,1,2,12)→?play?分布:yes(2 條)、no(2 條)mild(D2):6 條(索引 3,7,9,10,11,13)→?play?分布:yes(4 條)、no(2 條)cool(D3):4 條(索引 4,5,6,8)→?play?分布:yes(3 條)、no(1 條)
計算各子集的經驗熵:
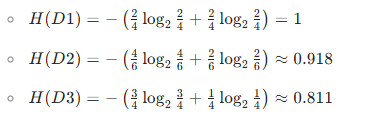
信息增益?IG(D,temperature):
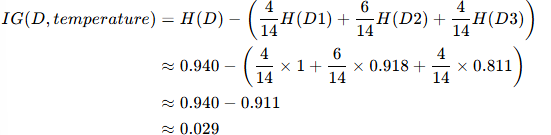
特征 3:humidity(取值:high、normal)
子集劃分:
high(D1):7 條(索引 0,1,2,3,7,11,13)→?play?分布:yes(3 條)、no(4 條)normal(D2):7 條(索引 4,5,6,8,9,10,12)→?play?分布:yes(6 條)、no(1 條)
計算各子集的經驗熵:
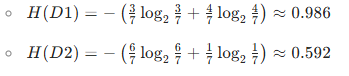
信息增益?IG(D,humidity):
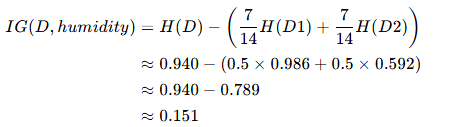
特征 4:windy(取值:FALSE、TRUE)
子集劃分:
FALSE(D1):8 條(索引 0,2,3,4,7,8,9,12)→?play?分布:yes(6 條)、no(2 條)TRUE(D2):6 條(索引 1,5,6,10,11,13)→?play?分布:yes(3 條)、no(3 條)
計算各子集的經驗熵:
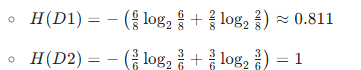
信息增益?IG(D,windy):
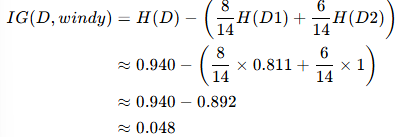
步驟 3:選擇信息增益最大的特征作為根節點
對比 4 個特征的信息增益:
- IG(outlook)≈0.246(最大)
- IG(humidity)≈0.151
- IG(windy)≈0.048
- IG(temperature)≈0.029
因此,根節點選?outlook。
步驟 4:遞歸劃分子集,構建子樹
對?outlook?的每個取值(sunny、overcast、rainy),遞歸重復上述過程(計算子集的經驗熵、信息增益,選最優特征)。
以?outlook=overcast?為例:
- 子集共 4 條樣本(索引 2,6,11,12),
play?全為?yes?→?已是純子集,直接生成葉節點?play=yes。
以?outlook=sunny?為例:
- 子集共 5 條樣本(索引 0,1,7,8,10),
play?分布:no(3 條)、yes(2 條)。 - 繼續計算該子集下各特征的信息增益(重復步驟 2),最終會選?
humidity?或其他特征進一步劃分,直到所有子集都 “純”(熵為 0)或無特征可分。
以?outlook=rainy?為例:
- 子集共 5 條樣本(索引 3,4,5,9,13),
play?分布:yes(3 條)、no(2 條)。 - 同樣遞歸計算信息增益,選擇最優特征(如?
windy?或?humidity?等)繼續劃分。
5. 最終決策樹結構
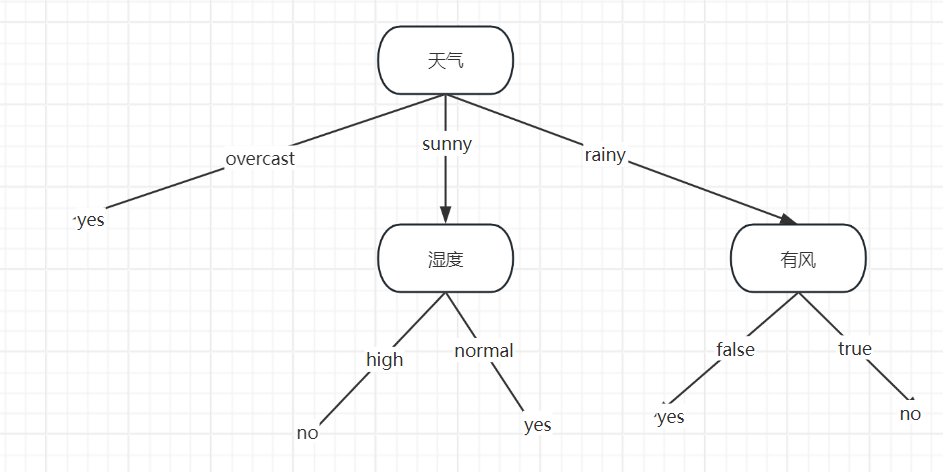
總結
ID3 算法通過?信息增益?選特征,優先拆分 “區分度最高” 的特征。對這個天氣數據集,根節點是?outlook,然后遞歸處理各子集,直到所有葉節點 “純”(熵為 0)。實際實現時,可通過代碼(如 Python +?scikit-learn?或手動遞歸)完整構建決策樹。
















)


