1、簡介

本文介紹了一種新的受自然啟發的優化算法，稱為灰熊增脂優化器（GBFIO）。GBFIO算法模仿灰熊積累體脂為過冬做準備的自然行為，利用它們的狩獵、捕魚和吃草、蜂蜜等策略。因此，GBFIO算法建模并考慮了三個數學步驟來解決最佳化問題：（1）根據過去的經驗和嗅覺線索尋找食物來源（例如蔬菜、水果、蜂蜜、牡蠣）；（2）獵殺動物并保護后代免受捕食者的傷害；和（3）捕魚。

2.灰熊增脂優化算法

首先，本節將描述GBFIO算法，接下來將說明其數學模型以優化各種優化問題。

2.1 GBFIO算法理論

熊必須在一年中溫暖的月份在體內儲存足夠的脂肪，以便在冬眠和幾個月不活動的寒冷月份養活自己。有幼崽的熊也必須在冬眠期間儲存足夠的脂肪來喂養幼崽，如果它們不能儲存足夠的脂肪，幼崽就會死亡。圖1顯示了一只灰熊和她的兩只幼崽，它們正在進食并試圖增加脂肪以在冬天生存。

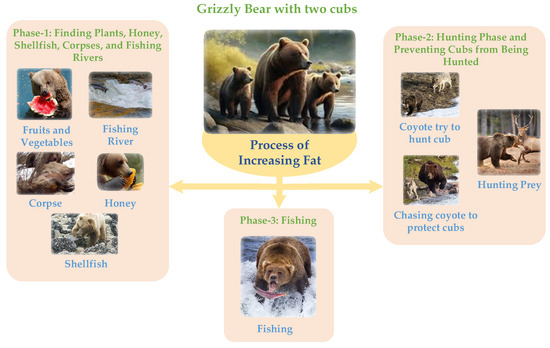
圖1.一只灰熊帶著兩只幼崽和增加脂肪的過程。
灰熊是雜食動物，它們的飲食依賴于可獲得的食物來源，除了捕魚和狩獵，棕熊以水果、樹根、貝類、蜂蜜等植物材料為食。
因此，灰熊脂肪的增加可分為以下三個階段，每一步都在熊體內儲存一些脂肪，直到達到冬眠所需的量（見圖1）：（1）根據前幾年的記憶和嗅覺，尋找蔬菜、水果、貝類、池塘、河流的位置進行捕魚，并跟蹤魚的運動；（2）獵殺其他動物，同時也照顧后代，以避免被獵殺；（3）捕魚（這是局部搜索）。因此，提出的基于灰熊脂肪增加的優化算法建模如下：

2.1.1第一階段：尋找植物、蜂蜜、貝類、尸體和釣魚河

灰熊增肥的主要飲食是魚，但在魚從海里到達產卵地和灰熊找到適合捕魚的地方之前，它們吃其他東西，包括蔬菜、水果、蜂蜜、貝類和死去的動物尸體。因此，通過吃蔬菜、水果、貝類等來增肥，同時也找到魚，模型如下：

$$x_{\text{bear}}^{\text{search}}(t+1)=x_{\text{bear}}^{\text{search}}(t)+r_1.\Delta x_{\text{fish}}+r_2.\Delta x_{\text{honey}}+r_3.\Delta x_{\text{shell}}+r_4.\Delta x_{\text{corpse}}+r_5.\Delta x_{\text{plants}}\text{\hspace{1em}(2)}$$

$$\Delta x_{\text{fish}}=x_{\text{fish}}?x_{\text{bear}}^{\text{search}}(t),\text{\hspace{1em}(3)}$$

$$\Delta x_{\text{honey}}=x_{\text{honey}}?x_{\text{bear}}^{\text{search}}(t),\text{\hspace{1em}(4)}$$

$$\Delta x_{\text{shell}}=x_{\text{shell}}?x_{\text{bear}}^{\text{search}}(t),\text{\hspace{1em}(5)}$$

$$\Delta x_{\text{corpse}}=x_{\text{corpse}}?x_{\text{bear}}^{\text{search}}(t),\text{\hspace{1em}(6)}$$

$$\Delta x_{\text{plants}}=x_{\text{plants}}?x_{\text{bear}}^{\text{search}}(t).\text{\hspace{1em}(7)}$$

其中 $x_{\text{fish}}$、$x_{\text{honey}}$、$x_{\text{shell}}$、$x_{\text{corpse}}$ 和 $x_{\text{plants}}$ 是魚、蜂蜜、貝殼、尸體和植物，熊試圖找到這些食物以增加脂肪并度過冬季。$x_{\text{bear}}^{\text{search}}(t)$ 是當前種群，最好的五個種群被選為 $x_{\text{fish}}$、$x_{\text{honey}}$、$x_{\text{shell}}$、$x_{\text{corpse}}$ 和 $x_{\text{plants}}$。當前迭代次數用 $t$ 表示。

此外，找到每種食物對熊來說都是具有挑戰性的，并且是隨機找到的，$r_1$ 到 $r_5$ 被定義為顯示每種食物來源的隨機狀態，因此 $r_1$ 到 $r_5$ 被定義如下：

$$r_1^s=2.\text{rand}.\sqrt{\text{rand}},\text{\hspace{1em}(8)}$$

$$r_2^s=\text{rand}.\sqrt{\text{rand}},\text{\hspace{1em}(9)}$$

$$r_3^s=\frac{\text{rand}}{2}.\sqrt{\text{rand}},\text{\hspace{1em}(10)}$$

$$r_4^s=\frac{\text{rand}}{4}.\sqrt{\text{rand}},\text{\hspace{1em}(11)}$$

$$r_5^s=\frac{\text{rand}}{8}.\sqrt{\text{rand}},\text{\hspace{1em}(12)}$$

其中 $\text{rand}$ 值在 [0, 1] 范圍內隨機選擇。$r_1$ 值比其他隨機值大，因為魚對熊來說是一種更有趣的食物，并且在脂肪增加方面具有高營養價值。因此，減少營養價值及其對增加脂肪的影響，其效應系數的值也減少，因此我們有 $r_1^s>r_2^s>r_3^s>r_4^s>r_5^s$。此外，$r_1^s$、$r_2^s$、$r_3^s$、$r_4^s$ 和 $r_5^s$ 的值分別在 [0, 2]、[0, 1]、[0, 0.5]、[0, 0.25]、[0, 125] 范圍內。

2.1.2. 狩獵階段和保護幼崽免受捕獵

灰熊的一種增肥方式是通過捕獵其他動物獲得的。母熊必須保持警惕，以保護幼崽免受潛在捕食者（包括郊狼和其他熊）的捕獵，這影響了狩獵過程。如果幼崽被殺，母熊在冬季需要更少的食物和脂肪，這也是模型的一部分。因此，狩獵熊的階段如下。

作為第一步，熊識別它們的獵物并朝它們移動。由于模擬熊的行為，所提出的 SBFIO 在搜索空間中搜索以發現各種搜索區域。SBFIO 的一個關鍵特征是獵物在搜索空間中的位置是隨機確定的。方程 (12) 模擬了熊如何移動到其目標以及這些概念如何工作。

$$\Delta x_{\text{bear}}=[2.r_1^b.x_{\text{hunt}}^{\text{num}}(t)?r_2^b.x_{\text{prey}}(t)],\text{\hspace{1em}(13)}$$

$$x_{\text{bear}}^{\text{hunt}}(t+1)=x_{\text{bear}}^{\text{hunt}}(t)?A.\Delta x_{\text{bear}},\text{\hspace{1em}(14)}$$

其中 $r_1^b$ 和 $r_2^b$ 是在 [0, 1] 范圍內隨機選擇的值。獵物越大，熊積累的脂肪越多；因此，為了最大化脂肪積累，最佳種群在前一更新步驟后獲得，被選為獵物。所以，$x_{\text{hunt}}^{\text{num}}$ 是當前種群，其中被選為熊的種群，試圖捕獵最佳獵物以增加其脂肪水平。$x_{\text{prey}}(t)$ 是從前一步驟更新的種群中獲得的最佳種群。$A$ 表示通過方程 (14) 計算的系數向量。

$$A=\alpha (2.r_3^b?1),\text{\hspace{1em}(15)}$$

其中 $\alpha$ 值在 [0, 2.5] 范圍內線性從 2.5 減少到 0，$r_3^b$ 顯示在 [0, 1] 范圍內的隨機值。

在第二步中，模擬了其他動物（包括郊狼）對幼崽的捕食。在這一步中，假設熊在狩獵過程中必須保護兩個幼崽，以防止它們被捕獵。如果幼崽被獵殺，母熊因不喂養幼崽而儲存更多脂肪。因此，當前種群，即母熊，如果幼崽被捕獵，則可以增加更多脂肪。從種群中隨機選擇三個個體作為幼崽和郊狼，并且，由于郊狼是捕食者并且比幼崽更強，這三個被選中的成員中最好的成員被選為郊狼，另外兩個成員被選為幼崽。因此，用郊狼捕獵幼崽的模型如下：

$$\Delta x_{\text{cub-1}}^{\text{cote}}=[2.r_4^b.x_{\text{cub}}^{(1)}?r_5^b.x_{\text{cote}}(t)],\text{\hspace{1em}(16)}$$

$$\Delta x_{\text{cub-2}}^{\text{cote}}=[2.r_6^b.x_{\text{cub}}^{(2)}?r_7^b.x_{\text{cote}}(t)],\text{\hspace{1em}(17)}$$

$$x_{\text{bear}}^{\text{carr}}(t+1)=x_{\text{bear}}^{\text{carr}}(t)?B_1.\Delta x_{\text{cub-1}}^{\text{cote}}?B_2.\Delta x_{\text{cub-2}}^{\text{cote}}\text{\hspace{1em}(18)}$$

$$B_1=B_2=\rho (2.r_8^b?1),\text{\hspace{1em}(19)}$$

其中 $x_{\text{cote}}^{\text{carr}}(t)$ 是在第一階段更新后的種群中被選為母熊以保存和增加其身體的當前種群，$x_{\text{cote}}(t)$ 是在這三個被選中的成員中最好的成員，$x_{\text{cub}}^{(1)}$ 和 $x_{\text{cub}}^{(2)}$ 是在這三個被選中的成員中隨機選擇的三個成員。($x_{\text{cote}}$ 是這三個被選中成員中最好的成員，而其他兩個成員被選為 $x_{\text{cub}}^{(1)}$、$r_4^b$、$r_5^b$、$r_6^b$ 和 $r_7^b$ 是 [0, 1] 范圍內的隨機向量。$B_1$ 和 $B_2$ 顯示通過方程 (17) 計算的系數向量。其中 $\rho$ 值在 [0, 1.25] 范圍內，并且在迭代過程中線性從 1.25 減少到 0。

在本節中，假設熊要么狩獵和增肥，要么熊可以通過失去幼崽來儲存更多脂肪。由于熊照顧幼崽，幼崽也可以通過逃跑和戰斗來生存。熊更有可能被郊狼或其他熊捕獵，這影響了狩獵過程。考慮到這一點，狩獵狀態被認為是幼崽被捕獵或丟失，因此我們有以下內容：

$$x_{\text{bear}}^{\text{hunting-care}}(t+1)=\{\begin{array}{ll}{x}_{\text{bear}}^{\text{hunt}}(t+1)& \text{if?}\beta \le 0.7\\ x_{\text{bear}}^{\text{carr}}(t+1)& \text{if?}\beta >0.7\end{array}\text{\hspace{1em}(20)}$$

其中 $\beta$ 是 [0, 1] 范圍內的隨機值。

2.1.3. 第三階段：捕魚

灰熊對魚有很強的偏好。每年，成千上萬的鮭魚遷徙上游產卵。這些魚為熊提供了它們需要生存的豐富脂肪和蛋白質。魚的豐富性幫助熊獲得它們需要度過冬季的體重。

灰熊沿著鮭魚的遷徙路徑定位自己，捕捉魚并躍入河中。每只熊占據一個特定位置，并能夠在半徑 $r$ 內的一個圓形捕魚區域內每天捕獲一定數量的魚。隨著冬季的臨近和結束，魚的數量減少，熊的脂肪增加到冬眠所需的量。因此，我們對以下內容進行建模：

$$x_{\text{bear}}^{\text{fishing}}(t+1)=(1+F).x_{\text{bear}}^{\text{fishing}}(t),\text{\hspace{1em}(21)}$$

$$F=\eta ?\cos (2.\pi .r_1^f),\text{\hspace{1em}(22)}$$

其中 $x_{\text{bear}}^{\text{fishing}}(t)$ 是第二階段后更新的當前種群，對應于參與捕魚以增加脂肪儲備的熊。項 $\cos (2.\pi .r_1^f)$ 用于模擬圓形捕魚區域，其中 $r_1^f$ 是 [0, 1] 范圍內的隨機值。參數 $\eta$ 在 [0, 1] 范圍內，表示在迭代過程中從 1 減少到 0 的衰減因子。衰減因子 $\eta$ 設置為 0.3。

成年灰熊每天大約捕獲 25 條魚。為了考慮每日捕魚量，$f^{\text{num}}$ 是每只熊每天的捕魚嘗試（或重復）次數。因此，我們對捕魚階段表示如下：

$$(x_{\text{bear}}^{\text{fishing}}(t+1){)}^{(f)}=(1+f^{\text{num}}.f^{\text{fishing}}(t){)}^{(f)},?f=[1,2,...,25],\text{\hspace{1em}(23)}$$

其中最大數量 $\gamma$ 等于 25。一般來說，在捕魚階段，每只熊更新 25 次。每次釣魚嘗試后，如果新生成的解決方案（位置）產生更好的適應度值，它會替換前一個。在本節中，提出了GBFIO算法的執行過程，步驟如下：

步驟1：設置輸入值，包括變量數量（n）、變量的最大值和最小值、最大迭代次數（Iter_max）和種群大小（N）。初始化建議的GBFIO算法參數，包括捕魚數量（f = 25）和 $\eta =0.3$。最后，設置以下參數的最大數量：$\alpha =2.5,\rho =1.25,\gamma =1$。

步驟2：在變量值范圍內隨機生成初始種群，如下所示：

$${\bar{X}}_{\text{pop}}=\text{rand}(1,n)?(X_{\text{max}}?X_{\text{min}})+X_{\text{min}}\text{\hspace{1em}(22)}$$

其中 $X_{\text{max}}$ 和 $X_{\text{min}}$ 是變量的最小值和最大值。$\text{rand}$ 顯示 [0, 1] 范圍內的隨機向量。此外，計算每個種群的目標函數。因此，計算主要種群后，該過程對每個參數重復。

步驟3：開始迭代并將迭代次數設置為 $i=1+\text{iteration}$。

步驟4：開始搜索階段，基于目標函數選擇前5個最佳成員，如魚、蜂蜜、貝殼、尸體和植物。根據方程 (1)-(11) 計算新的新搜索種群（每個種群被選為熊尋找食物）。

步驟5：計算步驟4中新計算種群的整個目標函數。如果每個新搜索種群的目標函數優于初始種群，則用步驟4中計算的新搜索種群更新初始種群。

步驟6：開始狩獵和護理階段。

步驟6.1-狩獵階段：從種群中選擇表現最佳的成員作為獵物，這將為熊提供最多的脂肪。根據方程 (12)-(14) 計算整個新的狩獵種群。

步驟6.2-護理階段：從種群中隨機選擇三個成員。在他們中，識別表現最佳的作為郊狼，其他兩個作為熊幼崽。根據方程 (15)-(17) 計算新的熊種群。

步驟6.3-根據方程 (18) 選擇狩獵和護理階段的新種群。如果生成的隨機數小于 0.7，則從狩獵階段 (步驟 6.1) 選擇新的狩獵和護理種群 ($x_{\text{bear}}^{\text{hunting-care}}$)；如果生成的隨機數大于 0.7，則從護理階段 (步驟 6.2) 選擇狩獵和護理種群 ($x_{\text{bear}}^{\text{nursing-care}}$)。

步驟7：計算步驟 6.3 中新計算種群的整個目標函數。如果每個新的狩獵和護理種群 ($x_{\text{bear}}^{\text{hunting-care}}$) 的目標函數優于更新后的初始種群，則用步驟 6 中計算的新狩獵和護理種群 ($x_{\text{bear}}^{\text{hunting-care}}$) 替換種群。

步驟8：開始捕魚階段。每個更新的種群代表一只每天捕魚 25 次的熊。將捕魚次數設置為 $f=1$。

步驟8.1：通過方程 (21) 計算新的捕魚種群，然后計算目標函數。

步驟8.2：如果每個捕魚種群 ($x_{\text{bear}}^{\text{fishing}}$) 的目標函數優于更新后的初始種群，則用新的捕魚種群 ($x_{\text{bear}}^{\text{fishing}}$) 替換種群。

步驟8.3：如果捕魚次數小于最大捕魚次數 (25)，則將捕魚次數 $f=f+1$ 并返回步驟 8.1。否則，轉到步驟 9。

步驟9：如果迭代次數小于最大迭代次數，則轉到步驟 4；否則轉到步驟 10。

步驟10：選擇更新種群中的最佳成員作為解決方案，然后結束過程。

提出的GBFIO算法的偽代碼在表 1 中描述。此外，GBFIO算法的流程圖如圖 2 所示。

```matlab
clc
clear all
pack
%%%%%%%%%% n is dimension of objective function
n = 30;
%%%%%%%%%% Define the Range of Variables
Xmax = ones(1,n) *100;
Xmin = ones(1,n)*(?100);
%%%%%%%%%% n is the Population Size
N = 150;
%%%%%%%%%% Maximum Number of Iteration
Iter_max = 500;
%%%%%%%%%% Define the GBFIO parameters
f = 2.5;
eta = 1.25;
Zeta = 0.3;
fishing_number = 25;
%%%%%%%%%% Generate the Initial Populations
for i = 1:NIpop(i,:) = rand(1,n).*(Xmax ? Xmin) + Xmin;cost(i,:) = sum(Ipop(i,:).^2);
end
%%%%%%%%%% Sort the Initial Populations Based on Cost Function
Ipop_mix = [Ipop,cost];
Ipop_sort = sortrows(Ipop_mix,n + 1);
%%%%%%%%%% Specify the Fish, Honey, Body, Shell, and Plants
Fish = Ipop_sort(1,:);
Honey = Ipop_sort(2,:);
Body = Ipop_sort(3,:);
Shell = Ipop_sort(4,:);
Plants = Ipop_sort(5,:);
%%%%%%%%%% Start the Iteration for Updating Populations
for iter = 1:Iter_maxfor i = 1:N%%%%%%%%%% Start the Searching Phaser1 = rand(1,n);deltax_fish = (2.*r1.*( (r1).^0.5)).*(Fish(1,[1:n]) ? Ipop(i,:));deltax_honey = (r1.*((r1).^0.5)).*(Honey(1,[1:n]) ? Ipop(i,:));deltax_body = (0.5.*r1.*((r1).^0.5)).*(Body(1,[1:n]) ? Ipop(i,:));deltax_shell = (0.25.*r1.*((r1).^0.5)).*(Shell(1,[1:n]) ? Ipop(i,:));deltax_plants = (0.125.*r1.*((r1).^0.5)).*(Plants(1,[1:n]) ? Ipop(i,:)); Xnew_search = Ipop(i,:) + deltax_fish + deltax_honey + deltax_body + deltax_shell + deltax_plants;Xnew_search = min(Xnew_search,Xmax);Xnew_search = max(Xnew_search,Xmin);cost_S = sum(Xnew_search.^2);%%%%%%%%%% Update the Populationif cost_S < cost(i,1)Ipop(i,:) = Xnew_search;cost(i,1) = cost_S;end%%%%%%%%%% End the Searching Phase%%%%%%%%%% Start the Hunting Phase%%%%% Start the Hunting Phase: Bear HuntingIpop_mix = [Ipop,cost];Ipop_sort = sortrows(Ipop_mix,n + 1);Prey = Ipop_sort(1,:);A = (f*(1-iter/Iter_max)).*(2.*rand(1,n) ? 1);D = abs(((2.*rand(1,n)).*Ipop(i,:))-(rand(1,n).*Prey(1,[1:n])));X_hunt = Ipop(i,:)-A.*D;X_hunt = min(X_hunt,Xmax);X_hunt = max(X_hunt,Xmin);cost_hunt = sum(X_hunt.^2);%%%%% Start the Hunting Phase: Coyote HuntingL = randperm(N);LL = find(L~ = i);LLL = L(LL);J1 = LL(1);J2 = LL(2);J3 = LL(3);I_child = [Ipop(J1,:),cost(J1,1);Ipop(J2,:),cost(J2,1);Ipop(J3,:),cost(J3,1)];I_chsort = sortrows(I_child,n + 1);A1 = (eta*(1-iter/Iter_max)).*(2.*rand(1,n) ? 1);A2 = (eta*(1-iter/Iter_max)).*(2.*rand(1,n) ? 1);D1 = abs(((2.*rand(1,n)).*I_chsort(2,[1:n])) ? (rand(1,n).*I_chsort(1,[1:n])));D2 = abs(((2.*rand(1,n)).*I_chsort(3,[1:n])) ? (rand(1,n).*I_chsort(1,[1:n])));X_ch = Ipop(i,:) ? (A1.*D1 + A2.*D2);X_ch = min(X_ch,Xmax);X_ch = max(X_ch,Xmin);cost_ch = sum(X_ch.^2);%%%%%%%%%% Update the PopulationG = rand(1,1);if G < 0.75if cost_hunt < cost(i,1)Ipop(i,:) = X_hunt;cost(i,1) = cost_hunt;endelseif cost_ch < cost(i,1)Ipop(i,:) = X_ch;cost(i,1) = cost_ch;endend%%%%%%%%%% End the Hunting Phase%%%%%%%%%% Start the Fishing Phasefor kk = 1:fishing_numberZ = Zeta*(1 ? iter/Iter_max)*cos(2*pi*rand(1,1));X_fish = (1 + Z).*Ipop(i,:);X_fish = min(X_fish,Xmax);X_fish = max(X_fish,Xmin);cost_fishing = sum(X_fish.^2);%%%%%%%%%% Update the Populationif cost_fishing < cost(i,1)Ipop(i,:) = X_fish;cost(i,1) = cost_fishing;endend%%%%%%%%%% Specify the Fish, Honey, Body, Shell, and Plants forIpop_mix = [Ipop,cost];Ipop_sort = sortrows(Ipop_mix,n + 1);Fish = Ipop_sort(1,:);Honey = Ipop_sort(2,:);Body = Ipop_sort(3,:);Shell = Ipop_sort(4,:);Plants = Ipop_sort(5,:);end%%%%%%%%%% Specify the Parameters of Convergence CurveConvergence_Curve(iter,1) = iter;Convergence_Curve(iter,2) = Ipop_sort(1,n + 1);
end
%%%%%%%%%% Print the Best Solution
Best = Ipop_sort(1,:);
plot(Convergence_Curve(:,1),Convergence_Curve(:,2))

Dehghani M, Aly M, Rodriguez J, Sheybani E, Javidi G. A Novel Nature-Inspired Optimization Algorithm: Grizzly Bear Fat Increase Optimizer. Biomimetics (Basel). 2025 Jun 7;10(6):379. doi: 10.3390/biomimetics10060379