
Diffusion Models 擴散模型
我們已經了解到,構建強大的生成模型的一種有效方法是:先引入一個關于潛在變量z的分布p(z),然后使用深度神經網絡將z變換到數據空間x。由于神經網絡具有通用性,能夠將簡單固定的分布轉化為關于x的高度靈活的分布族,因此為p(z)采用如高斯分布N(z|0, I)這類簡單固定的分布就足夠了。在之前的章節中,我們探討了多種符合這一框架的模型,這些模型基于生成對抗網絡、變分自編碼器以及歸一化流,在定義和訓練深度神經網絡方面采用了不同的方法。
在本章中,我們將探討這一通用框架下的第四類模型,即擴散模型(diffusion models),也被稱為去噪擴散概率模型(denoising diffusion probabilistic models,簡稱DDPMs)(Sohl-Dickstein等人,2015年;Ho、Jain和Abbeel,2020年)。這類模型已成為許多應用領域中最先進的模型。為便于說明,我們將重點討論圖像數據模型,盡管該框架具有更廣泛的適用性。其核心思想是,對每張訓練圖像應用多步加噪過程,將其逐步破壞并最終轉化為一個服從高斯分布的樣本。這一過程如圖20.1所示。隨后,訓練一個深度神經網絡來逆轉這一過程;一旦訓練完成,該網絡就可以從高斯分布中采樣作為輸入,進而生成新的圖像。
擴散模型可被視為一種分層變分自編碼器的變體,其中編碼器分布是固定的,由加噪過程所定義,而僅需學習生成分布(Luo,2022)。這類模型易于訓練,在并行硬件上擴展性良好,且能規避對抗訓練中的挑戰與不穩定性問題,同時生成結果的質量可與生成對抗網絡相媲美甚至更優。然而,由于需要通過解碼器網絡進行多次前向傳播,生成新樣本的計算成本可能較高(Dhariwal和Nichol,2021)。
20.1 Forward Encoder 前向編碼器
假設我們從訓練集中選取一張圖像,記為 x,然后對每個像素獨立地添加高斯噪聲進行混合,得到一個受噪聲干擾的圖像 z?,其定義如下:
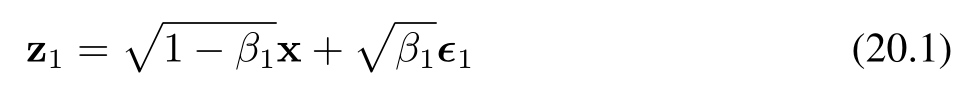
其中,ε? ~ N(ε?|0, I),且 β? < 1 為噪聲分布的方差,β? ∈ (0,1):控制噪聲強度的超參數(稱為噪聲的方差系數)。公式(20.1)和(20.3)中系數 √(1 ? β?) 和 √β? 的選取,確保了 z? 的分布均值相較于 z??? 更接近零,且 z? 的協方差矩陣相較于 z??? 更接近單位矩陣。我們可以將變換(20.1)改寫為如下形式:
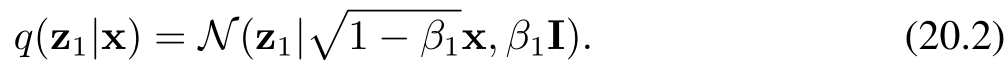
隨后,我們通過多次添加獨立的加性高斯噪聲,重復這一過程,從而生成一系列噪聲逐步增強的圖像序列 z?, …, z?。需要注意的是,在擴散模型的相關文獻中,這些潛在變量有時被記為 x?, …, x?,而觀測變量則記為 x?。為與本書其余部分保持一致,我們采用 z 表示潛在變量、x 表示觀測變量的符號體系。每一幅后續圖像的生成方式如下:
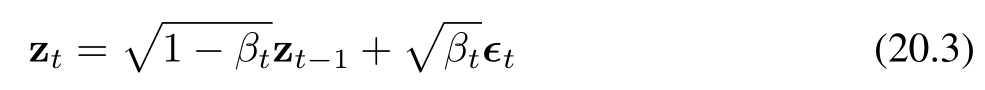
其中,ε? ~ N(ε?|0, I)。同樣地,我們可以將公式(20.3)改寫為如下形式:
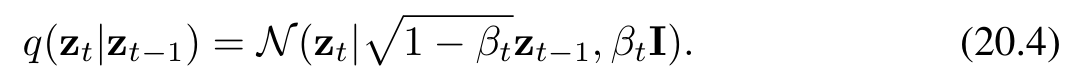
條件分布序列(20.4)構成一個馬爾可夫鏈,并可用如圖20.2所示的概率圖模型表示。方差參數 β? ∈ (0, 1) 需手動設定,通常按照預設的遞增規則選擇,使得方差值沿鏈逐步增大,即滿足 β? < β? < … < β?。
這個公式描述的是擴散模型(Diffusion Model)中的前向過程(Forward Process),即如何逐步向原始圖像添加噪聲,最終將其轉化為純噪聲。詳細解析公式和方差參數空間門
公式 (20.3)
zt=1?βtzt?1+βt?tz_t = \sqrt{1 - \beta_t} z_{t-1} + \sqrt{\beta_t} \epsilon_tzt?=1?βt??zt?1?+βt???t?
- ztz_tzt? 和 zt?1z_{t-1}zt?1?:分別表示在時間步 ttt 和 t?1t-1t?1 的圖像(或潛在變量)。
- βt\beta_tβt?:是一個預先設定的參數,取值范圍在 (0,1)(0, 1)(0,1) 之間,控制每一步添加噪聲的比例。
- ?t\epsilon_t?t?:是從標準正態分布 N(?t∣0,I)\mathcal{N}(\epsilon_t | 0, \mathbf{I})N(?t?∣0,I) 中采樣得到的高斯噪聲,其中 I\mathbf{I}I 是單位矩陣。
這個公式的含義是,在每一步 ttt,當前的圖像 ztz_tzt? 是由前一步的圖像 zt?1z_{t-1}zt?1? 加上一定比例的高斯噪聲 βt?t\sqrt{\beta_t} \epsilon_tβt???t? 得到的,同時保留了前一步圖像的一部分 1?βtzt?1\sqrt{1 - \beta_t} z_{t-1}1?βt??zt?1?。
公式 (20.4)
q(zt∣zt?1)=N(zt∣1?βtzt?1,βtI)q(z_t | z_{t-1}) = \mathcal{N}(z_t | \sqrt{1 - \beta_t} z_{t-1}, \beta_t \mathbf{I})q(zt?∣zt?1?)=N(zt?∣1?βt??zt?1?,βt?I)
這個公式是從概率的角度描述了公式 (20.3)。它表示在給定 zt?1z_{t-1}zt?1? 的條件下,ztz_tzt? 的條件概率分布是一個均值為 1?βtzt?1\sqrt{1 - \beta_t} z_{t-1}1?βt??zt?1?,協方差矩陣為 βtI\beta_t \mathbf{I}βt?I 的高斯分布。
參數 βt\beta_tβt? 的設定
參數 βt\beta_tβt? 是手動設定的,并且通常按照一個預設的遞增規則選擇,使得 β1<β2<?<βT\beta_1 < \beta_2 < \cdots < \beta_Tβ1?<β2?<?<βT?。這意味著隨著時間步 ttt 的增加,添加的噪聲比例逐漸增大,最終在 t=Tt = Tt=T 時,圖像幾乎完全轉化為噪聲。
通過這種方式,擴散模型的前向過程逐步將原始圖像轉化為一個各向同性的高斯分布,為后續的逆向生成過程(即從噪聲中恢復圖像)奠定了基礎。
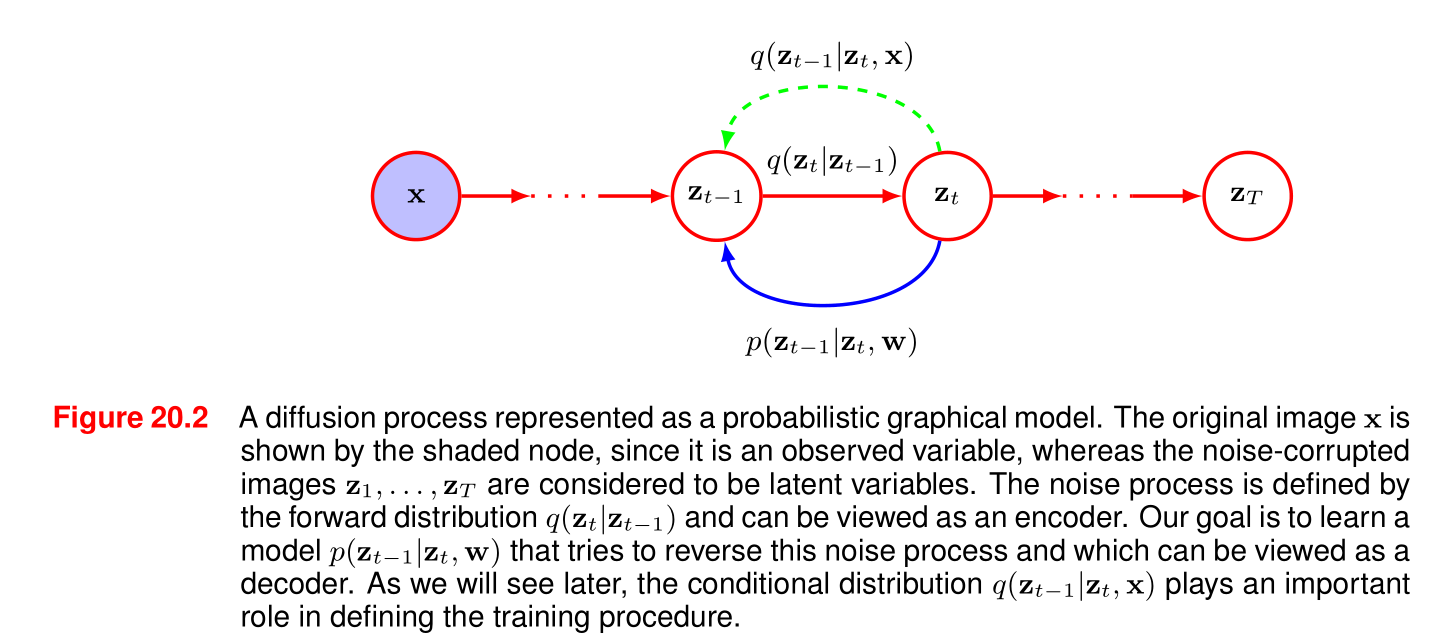
圖20.2 一個表示為概率圖模型的擴散過程。原始圖像x\mathbf{x}x由陰影節點表示,因為它是一個觀測變量,而受噪聲干擾的圖像z1,…,zTz_1, \ldots, z_Tz1?,…,zT?被視為潛在變量。噪聲過程由前向分布q(zt∣zt?1)q(z_t|z_{t - 1})q(zt?∣zt?1?)定義,可被視為一個編碼器。我們的目標是學習一個模型p(zt?1∣zt,w)p(z_{t - 1}|z_t, \mathbf{w})p(zt?1?∣zt?,w),該模型試圖逆轉這個噪聲過程,可被視為一個解碼器。正如我們稍后將看到的,條件分布q(zt?1∣zt,x)q(z_{t - 1}|z_t, \mathbf{x})q(zt?1?∣zt?,x)在定義訓練過程中起著重要作用。
圖的解析
這張圖展示了一個用概率圖模型表示的擴散過程。
-
節點和變量:
- 圖中左側的藍色陰影節點表示原始圖像 x\mathbf{x}x,它是一個觀測變量。
- 紅色節點 z1,…,zTz_1, \ldots, z_Tz1?,…,zT? 表示受噪聲干擾的圖像,被視為潛在變量。
-
過程描述:
- 前向過程(噪聲添加過程):由前向分布 q(zt∣zt?1)q(z_t | z_{t - 1})q(zt?∣zt?1?) 定義,可以看作是一個編碼器。從原始圖像 x\mathbf{x}x 開始,通過一系列步驟逐步添加噪聲,最終在 TTT 步后得到一個接近純噪聲的潛在變量 zTz_TzT?。圖中綠色虛線箭頭表示了這一前向過程的方向,即從 zt?1z_{t-1}zt?1? 到 ztz_tzt? 的噪聲添加步驟。
- 逆向過程(生成過程):目標是學習一個模型 p(zt?1∣zt,w)p(z_{t - 1} | z_t, \mathbf{w})p(zt?1?∣zt?,w),試圖逆轉這個噪聲添加過程,可以看作是一個解碼器。圖中藍色實線箭頭表示了逆向過程的方向,即從 ztz_tzt? 恢復到 zt?1z_{t - 1}zt?1? 的步驟。
-
條件分布的作用:
- 條件分布 q(zt?1∣zt,x)q(z_{t - 1} | z_t, \mathbf{x})q(zt?1?∣zt?,x) 在定義訓練過程中起著重要作用。它結合了觀測變量 x\mathbf{x}x 的信息,幫助模型學習如何從噪聲潛在變量 ztz_tzt? 恢復到前一步的潛在變量 zt?1z_{t - 1}zt?1?。
總體而言,這張圖直觀地展示了擴散模型中前向的噪聲添加過程和逆向的生成過程,以及各個變量和分布之間的關系。
20.1.1 Diffusion kernel
在給定觀測數據向量 x\mathbf{x}x 的條件下,潛在變量的聯合分布由下式給出: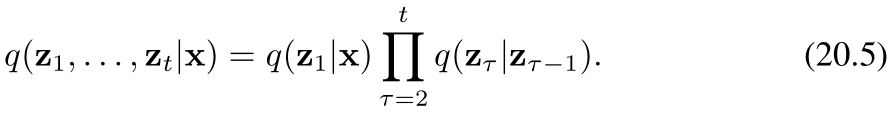
如果我們現在對中間變量 z1,…,zt?1z_1, \ldots, z_{t - 1}z1?,…,zt?1? 進行邊緣化處理(邊緣化處理的目的是消除中間變量,從而得到僅關于 ztz_tzt? 和 x\mathbf{x}x 的條件概率分布 q(zt∣x)q(\mathbf{z}_t | \mathbf{x})q(zt?∣x)),就得到了擴散核:
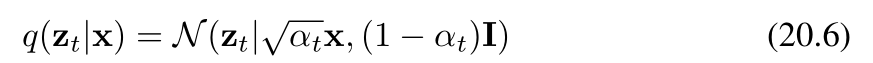
在此我們定義:

我們看到,每個中間分布都有一個簡單的閉式高斯表達式,我們可以直接從中進行采樣。這在訓練去噪擴散概率模型(Denoising Diffusion Probabilistic Models, DDPMs)時將被證明是很有用的,因為它允許使用馬爾可夫鏈中隨機選擇的中間項來進行高效的隨機梯度下降,而無需運行整個鏈。我們還可以將公式(20.6)寫成如下形式
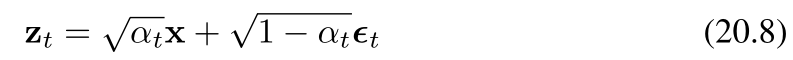
其中再次(有)?t~N(?t∣0,I)\epsilon_t \sim \mathcal{N}(\epsilon_t|0, \mathbf{I})?t?~N(?t?∣0,I)(這里表示?t\epsilon_t?t?服從均值為0、協方差矩陣為單位矩陣I\mathbf{I}I的多元正態分布)。請注意,此時?t\epsilon_t?t?代表添加到原始圖像上的總噪聲,而不是在馬爾可夫鏈的這一步添加的增量噪聲。
經過許多步驟后,圖像變得與高斯噪聲無法區分,當步數 TTT 趨于無窮大(T→∞T \to \inftyT→∞)時,我們有(以下情況/結果)

因此,關于原始圖像的所有信息都丟失了。公式 (20.3) 中系數 1?βt\sqrt{1 - \beta_t}1?βt?? 和 βt\sqrt{\beta_t}βt?? 的選擇確保了一旦馬爾可夫鏈收斂到一個均值為0、協方差為單位矩陣的分布,進一步的更新將不會改變這一分布。
由于公式 (20.9) 的右側與 x\mathbf{x}x(或 x,根據上下文確定具體變量)無關,因此可以得出 zTz_TzT?(或 zT\mathbf{z}_TzT? ,根據上下文確定具體變量)的邊緣分布由以下式子給出(或可表示為)

人們通常將馬爾可夫鏈(公式20.4)稱為前向過程,它類似于變分自動編碼器(VAE)中的編碼器,只不過這里(馬爾可夫鏈所代表的過程)是固定的,而非通過學習得到的。然而,需要注意的是,文獻中的常用術語與標準化流(normalizing flows)相關文獻中通常使用的術語是相反的,在標準化流的文獻中,從潛在空間到數據空間的映射被視為前向過程。
20.1.2 Conditional distribution 條件擴散
我們的目標是學會逆轉(消除、還原)加噪過程,因此很自然地會考慮條件分布 q(zt∣zt?1)q(z_t | z_{t - 1})q(zt?∣zt?1?) 的逆過程,我們可以借助貝葉斯定理將其表示為如下形式
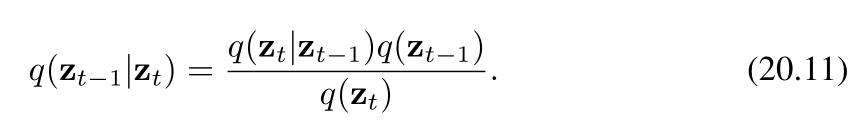
我們可以將邊緣分布 q(zt?1)q(z_{t-1})q(zt?1?) 表示為如下形式
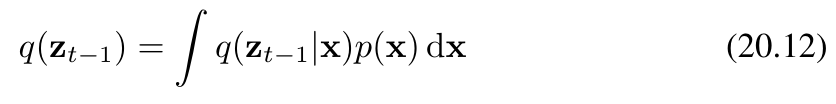
其中,q(zt?1∣x)q(z_{t-1}|\mathbf{x})q(zt?1?∣x) 由條件高斯分布(公式20.6)給出。然而,該分布難以直接處理(無法解析求解),因為我們必須對未知的數據分布 p(x)p(\mathbf{x})p(x) 進行積分。如果我們使用訓練數據集中的樣本對積分進行近似,則會得到一個復雜的分布,該分布可表示為高斯混合分布。
相反,我們考慮反向分布的條件版本,即在給定數據向量 x\mathbf{x}x 的條件下,定義為 q(zt?1∣zt,x)q(z_{t-1}|z_t, \mathbf{x})q(zt?1?∣zt?,x) 的分布。我們很快將會看到,該分布實際上是一個簡單的高斯分布。從直覺上看,這是合理的:因為給定一張含噪圖像時,很難推測出是哪張低噪聲圖像生成了它;而如果我們還知道原始(起始)圖像,那么問題就會變得簡單得多。我們可以利用貝葉斯定理來計算這個條件分布:
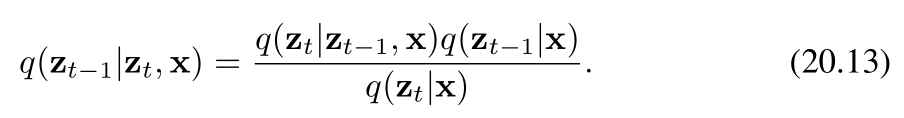
現在,我們利用前向過程的馬爾可夫性質來進行推導(ztz_tzt?只和前一時刻zt?1z{t-1}zt?1有關,與x無關)
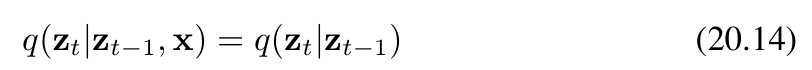
其中,等式右側由(20.4)式給出。作為 zt?1z_{t-1}zt?1? 的函數,它呈現為二次型的指數形式。(20.13)式分子中的 q(zt?1∣x)q(z_{t-1}|\mathbf{x})q(zt?1?∣x) 項是由(20.6)式給出的擴散核,它同樣涉及關于 zt?1z_{t-1}zt?1? 的二次型指數。由于(20.13)式的分母作為 zt?1z_{t-1}zt?1? 的函數是常數,我們可以忽略它。因此,我們看到(20.13)式的右側呈現為高斯分布的形式,并且我們可以使用“配方法”來確定其均值和協方差,具體如下:
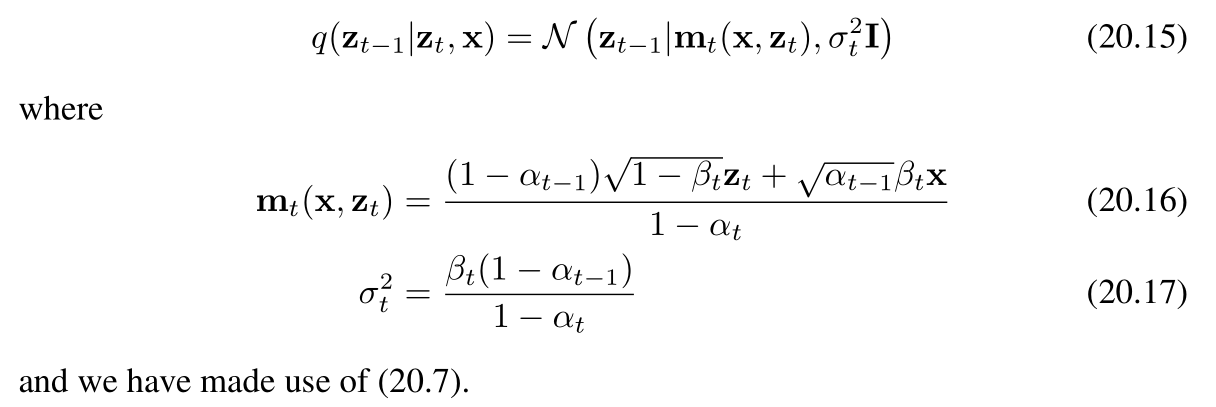
上述條件分布的轉化,化簡解釋秘籍——》寶典

)




)
和集群標簽(Cluster Tag))
)



仿抖音快手App的把位圖數據轉存為圖片)





)
