效果一覽
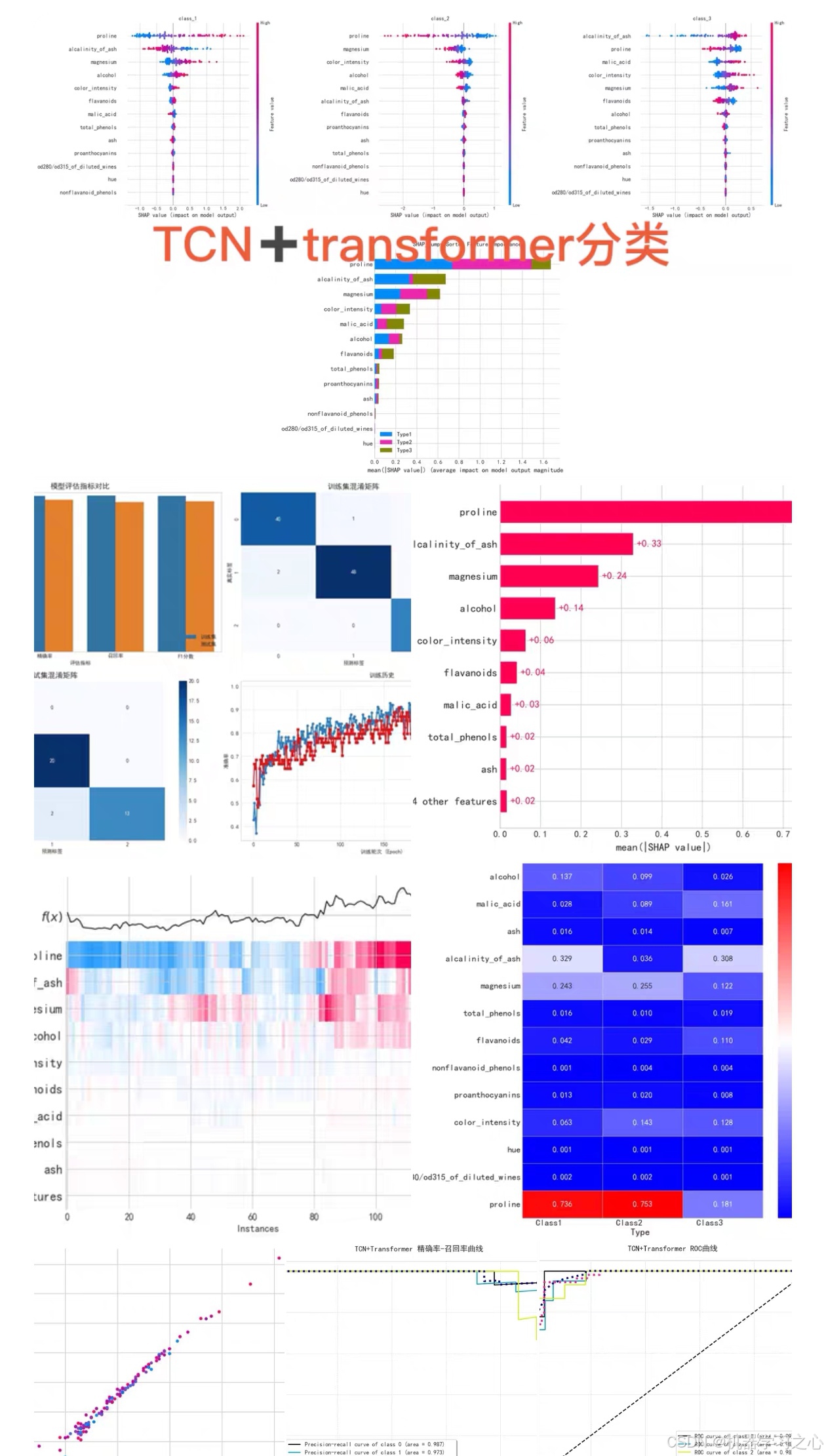
TCN+Transformer+SE注意力機制多分類模型 + SHAP特征重要性分析
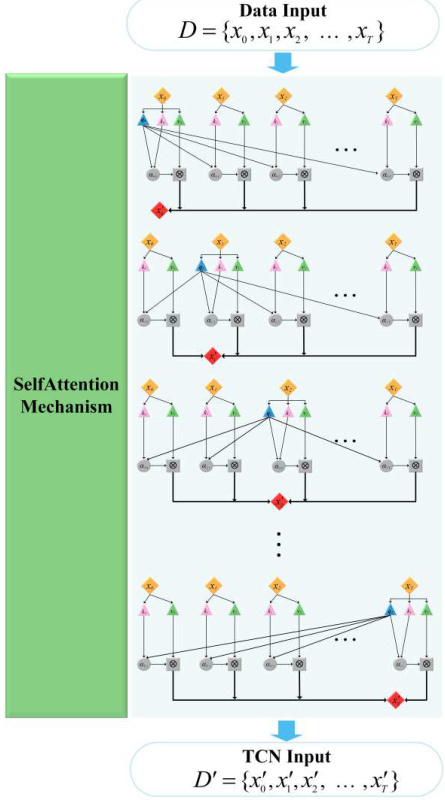
TCN(時序卷積網絡)的原理與應用
1. 核心機制
- 因果卷積:確保時刻 t t t 的輸出僅依賴 t ? 1 t-1 t?1 及之前的數據,避免未來信息泄露,嚴格保持時序因果性 。
- 空洞卷積:通過指數膨脹率(如 2 k 2^k 2k)擴大感受野,小卷積核即可捕獲長距離依賴(如 k = 4 k=4 k=4 時感受野達16)。
- 殘差連接:解決深層網絡梯度消失問題,公式為 O u t p u t = A c t i v a t i o n ( x + F ( x ) ) Output = Activation(x + F(x)) Output=Activation(x+F(x)),其中 F ( x ) F(x) F(x) 為卷積操作 。
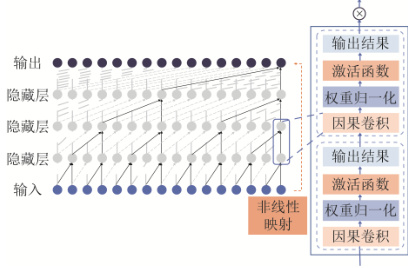
2. 數學表示
給定輸入序列 x x x 和卷積核 w w w,卷積輸出為:
y i = f ( x i ? w ) y_i = f(x_i \cdot w) yi?=f(xi??w)
其中 f ( ? ) f(\cdot) f(?) 為ReLU等激活函數, x i x_i xi? 為第 i i i 個時序點 。
3. 多分類任務優勢
- 并行計算:一維卷積支持高并發,訓練速度顯著優于RNN 。
- 長時序建模:在電價預測、負荷預測等任務中,TCN對長距離依賴的捕捉精度比CNN提升8%-15% 。
Transformer的全局依賴建模
1. 自注意力機制
-
核心公式:
Attention ( Q , K , V ) = softmax ( Q K T d k ) V \text{Attention}(Q,K,V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V Attention(Q,K,V)=softmax(dk??QKT?)V其中 Q , K , V Q,K,V Q,K,V 為查詢、鍵、值矩陣, d k d_k dk? 為維度縮放因子 。
-
多頭注意力:并行執行多組注意力,融合不同子空間特征,增強表達能力 。
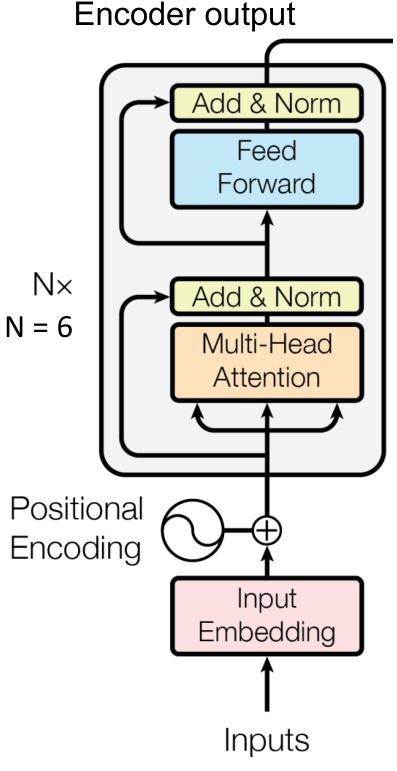
2. 位置編碼
注入時序信息的位置編碼公式:
P E ( p o s , 2 i ) = sin ? ( p o s / 1000 0 2 i / d ) , P E ( p o s , 2 i + 1 ) = cos ? ( p o s / 1000 0 2 i / d ) PE_{(pos,2i)} = \sin(pos/10000^{2i/d}), \quad PE_{(pos,2i+1)} = \cos(pos/10000^{2i/d}) PE(pos,2i)?=sin(pos/100002i/d),PE(pos,2i+1)?=cos(pos/100002i/d)
確保模型感知序列順序 。
3. 編碼器結構
- 輸入 → 嵌入層 + 位置編碼 → N × N \times N×(多頭注意力 + 前饋網絡)→ 輸出
- 每層含殘差連接(Add)與層歸一化(Norm),加速收斂 。
SE注意力機制的特征動態加權
1. 工作流程
-
壓縮(Squeeze) :全局平均池化壓縮空間維度,通道 c c c 輸出 z c = 1 H × W ∑ i = 1 H ∑ j = 1 W x c ( i , j ) z_c = \frac{1}{H \times W} \sum_{i=1}^H \sum_{j=1}^W x_c(i,j) zc?=H×W1?∑i=1H?∑j=1W?xc?(i,j) 。
-
激勵(Excitation) :全連接層學習通道權重:
s = σ ( W 2 δ ( W 1 z ) ) s = \sigma(W_2 \delta(W_1 z)) s=σ(W2?δ(W1?z))其中 δ \delta δ 為ReLU, σ \sigma σ 為Sigmoid, W 1 , W 2 W_1, W_2 W1?,W2? 為可學習參數 。
-
縮放(Scale) :特征圖按權重縮放: x ~ c = s c ? x c \tilde{x}_c = s_c \cdot x_c x~c?=sc??xc? 。
2. 分類任務價值
- 在鋰電池SOC估計中,SE模塊使關鍵通道權重提升30%,誤差降低12% 。
- 抑制噪聲通道,增強判別性特征(如圖像融合任務)。
多分類模型融合架構設計
1. 整體架構(TCN + Transformer + SE)
graph LR
A[輸入序列] --> B(TCN層:局部特征提取)
B --> C[SE模塊:通道加權]
C --> D(Transformer編碼器:全局依賴建模)
D --> E[全局平均池化]
E --> F[Softmax分類層]
2. 關鍵設計細節
- TCN層配置:
- 堆疊4-8個殘差塊,每塊含空洞卷積(膨脹率 2 k 2^k 2k)和因果卷積 。
- 輸出維度與Transformer輸入對齊(如256維)。
- SE模塊插入位置:
- 在TCN每個殘差塊后添加,動態調整卷積特征通道 。
- Transformer優化:
- 僅用編碼器,層數 N = 4 N=4 N=4,頭數 h = 8 h=8 h=8,前饋網絡維度 d f f = 512 d_{ff}=512 dff?=512 。
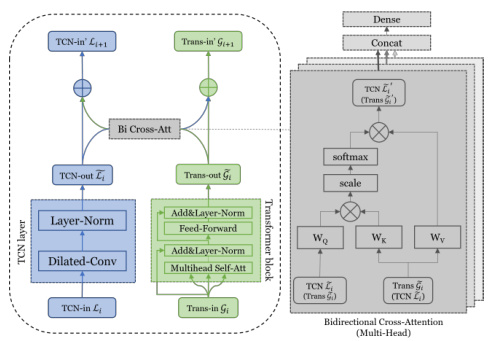
- 僅用編碼器,層數 N = 4 N=4 N=4,頭數 h = 8 h=8 h=8,前饋網絡維度 d f f = 512 d_{ff}=512 dff?=512 。
3. 分類層
-
全局平均池化 → 全連接層 → Softmax輸出多分類概率:
P ( y i ∣ x ) = e W i T x + b i ∑ j = 1 K e W j T x + b j P(y_i|x) = \frac{e^{W_i^T x + b_i}}{\sum_{j=1}^K e^{W_j^T x + b_j}} P(yi?∣x)=∑j=1K?eWjT?x+bj?eWiT?x+bi??其中 K K K 為類別數 。
SHAP特征重要性分析
1. SHAP原理
-
Shapley值計算:
特征 j j j 的SHAP值 ? j \phi_j ?j? 為所有特征子集 S S S 的邊際貢獻加權平均:
? j = ∑ S ? F ? { j } ∣ S ∣ ! ( ∣ F ∣ ? ∣ S ∣ ? 1 ) ! ∣ F ∣ ! ( v ( S ∪ { j } ) ? v ( S ) ) \phi_j = \sum_{S \subseteq F \setminus \{j\}} \frac{|S|!(|F|-|S|-1)!}{|F|!} (v(S \cup \{j\}) - v(S)) ?j?=S?F?{j}∑?∣F∣!∣S∣!(∣F∣?∣S∣?1)!?(v(S∪{j})?v(S))其中 F F F 為特征全集, v v v 為模型輸出函數 。
-
深度學習適配:
通過梯度積分(Integrated Gradients)或DeepSHAP算法逼近復雜模型 。
2. 實施步驟
-
模型訓練:完成TCN-Transformer-SE模型訓練并保存。
-
SHAP值計算:
import shap explainer = shap.DeepExplainer(model, background_data) shap_values = explainer.shap_values(test_data) -
可視化分析:
- 摘要圖(Summary Plot) :特征全局重要性排序 。
- 依賴圖(Dependence Plot) :分析特征交互效應(如IRI_0與Pt_A的負相關)。
- 樣本決策圖:解釋單樣本預測(如錯分樣本歸因)。
3. 多分類場景應用
- 按類別分析:對每個類別獨立計算SHAP值,識別類別敏感特征 。
- 關鍵發現示例:
- 在航空發動機RUL預測中,前5個特征的SHAP貢獻占比87.25% 。
- 高初始IRI值(IRI_0)正相關于路面退化速度(SHAP值>0.3)。
結論
TCN-Transformer-SE模型通過局部卷積+全局注意力+動態特征加權的三級架構,顯著提升長時序多分類任務的精度。結合SHAP可解釋性分析,既可量化特征貢獻(如通道權重、時間點重要性),又能指導模型優化(如冗余特征剔除)。該架構在電力、交通、金融等領域具廣泛應用潛力,未來可探索輕量化部署與實時預測場景。
支持多類別分類任務,適用于光譜分類、表格數據分類、時間序列分類等場景。
可自定義類別數量
輸出訓練損失和準確率,并評估訓練集和測試集的準確率,精確率,召回率,f1分數,繪制roc曲線,混淆矩陣
結合SHAP(Shapley Additive exPlanations),直觀展示每個特征對分類結果的影響!
包括蜂巢圖,重要性圖,單特征力圖,決策圖,熱圖,瀑布圖等





)
-)




)
![???????6板塊公共數據典型應用場景【政務服務|公共安全|公共衛生|環境保護|金融風控|教育科研]](http://pic.xiahunao.cn/???????6板塊公共數據典型應用場景【政務服務|公共安全|公共衛生|環境保護|金融風控|教育科研])






