【論文閱讀筆記】萬花筒：用于異構多智能體強化學習的可學習掩碼

摘要
在多智能體強化學習（MARL）中，通常采用參數共享來提高樣本效率。然而，全參數共享的流行方法通常會導致智能體之間的策略同質，這可能會限制從策略多樣性中獲得的性能優勢。為了解決這一關鍵限制，我們提出了萬花筒，一種新的自適應部分參數共享方案，在保持高樣本效率的同時促進策略異質性。具體來說，萬花筒為不同的智能體維護一組公共參數以及多組不同的、可學習的掩碼，決定參數的共享。它通過鼓勵這些掩碼之間的差異來促進策略網絡之間的多樣性，而不會犧牲參數共享的效率。這種設計使萬花筒能夠動態平衡高樣本效率和廣泛的策略表示能力，有效地彌合了各種環境中全參數共享和非參數共享之間的差距。我們進一步將萬花筒擴展到Actor-Critic算法背景下的批評器集合，這有助于提高價值估計。我們在廣泛的環境中進行了實證評估，包括多智能體粒子環境，多智能體MuJoCo和星際爭霸多智能體挑戰v2，與現有的參數共享方法相比，萬花筒的性能優越，展示了其在MARL中的性能增強潛力。該代碼可在Github上訪問。
1 引言
協作式多智能體強化學習（MARL）在解決各種領域復雜的現實世界決策問題方面表現出顯著的有效性，例如資源分配、包裹遞送、自動駕駛和機器人控制。為了緩解MARL典型的非平穩和部分可觀察環境帶來的挑戰（Yuan等人，2023），集中式訓練與分散執行（CTDE）范式已經變得普遍，激發了許多有影響力的MARL算法，如MADDPG 、COMA 、MATD3 、QMIX 和MAPPO 。
在CTDE范式下，智能體之間的參數共享是提高樣本效率的常用方法。然而，跨智能體的相同網絡參數往往導致同質策略，限制了行為的多樣性和整體聯合策略的表示能力。在某些情況下，這種限制會導致意想不到的結果，如圖1所示，阻礙進一步的性能增加。另一種方法是無參數共享方案，其中每個智能體擁有自己的唯一參數。然而，盡管這種方法自然地支持異構策略，但它受到樣本效率降低的影響，導致顯著的訓練成本。考慮到當前模型規模越來越大的趨勢，其中一些擴展到數萬億個參數，這尤其成問題。因此，必須開發一種既具有高樣本效率又具有廣泛策略表征能力的參數共享策略，從而有可能顯著提高性能。雖然一些努力已經探索了在訓練開始時啟動的部分參數共享，但是如果沒有對智能體特定環境轉換或獎勵函數的詳細了解，這種初始化設計可能具有挑戰性。在這里插入圖片描述
圖1：全參數共享限制策略是同構的。在這個例子中，所有的捕食者都追逐同一個獵物，而忽略了游戲世界中的另一個獵物。更多游戲細節見附錄A.2。
在這項工作中，我們建立在以前研究的見解基礎上，提出了一種新的自適應部分參數共享方案萬花筒。它維護一組策略參數，并使用多個可學習掩碼來指定共享參數。與早期依賴于固定初始化的方法不同，Kaleidoscope在整個訓練過程中動態地學習這些掩碼以及MARL參數。這種端到端訓練方法固有地集成了環境信息，其自適應特性使萬花筒能夠根據環境的需求和智能體的學習進度動態調整參數共享的水平。可學習掩碼促進了全參數共享和非參數共享之間的動態平衡，通過增強異質性在樣本效率和策略表征能力之間提供了靈活的權衡。首先，我們在智能體網絡上構建萬花筒，實現多種策略。在這一成功之后，我們將其擴展到多智能體Actor-Critic算法，以鼓勵中心批評器集合之間的異質性，從而進一步提高性能。

【注】：就像萬花筒利用旋轉鏡子的反射特性將簡單的形狀轉化為美麗的圖案一樣，我們提出的方法利用可學習的掩碼將一組參數映射到不同的策略中，從而提高任務性能。

我們的貢獻總結如下：

為了實現智能體之間策略的異構性以獲得更好的訓練靈活性，我們采用軟閾值重參數化（STR）技術，在只保留一組公共參數的情況下，為不同的智能體網絡學習不同的掩碼，有效地平衡了全參數共享和非參數共享機制。
為了增強智能體之間的策略多樣性，我們引入了一個新的正則化項來鼓勵掩碼之間的兩兩差異。此外，我們設計了重置機制，回收屏蔽參數以保持聯合網絡的表示能力。
通過在MARL基準上的大量實驗，包括多智能體粒子環境（MPE），MAMuJoCo 和在《星際爭霸》多智能體挑戰v2 (SMACv2) ，我們展示了Kaleidoscope優于現有參數共享方法的性能。

2 背景
多智能體強化學習（MARL） 在MARL中，完全協作的部分可觀察多智能體任務通常被表述為分散的部分可觀察馬爾可夫決策過程，由元組 $\mathcal{M}=\langle\mathcal{S},A,P,R,\Omega,O,N,\gamma\rangle$ 表示。其中，N為智能體的數量， $\gamma\in(0,1]$ 表示折現系數。在每個時間步t上，隨著環境狀態 $s^{t}\in\mathcal{S}$ ，智能體 $i$ 從觀測函數 $O(s^{t},i)$ 接收局部觀測 $o_i^t\in\Omega$ 然后遵循本地策略 $\pi_{i}$ 選擇動作 $a_{i}^{t}\in A$ 。個體動作形成聯合動作 $a^{t}\in A^{N}$ 。導致狀態轉換到下一個狀態 $s^{t+1}\sim P(s^{t+1}|s^{t},\boldsymbol{a}^{t})$ 并包含一個全局獎勵 $r^{t}=R(s^{t},\boldsymbol{a}^{t})$ 。整個團隊的目標是學習聯合策略 $\boldsymbol{\pi}=\langle\pi_1,\ldots,\pi_N\rangle$ 從而最大化折現累計獎勵的期望 $G^t=\sum_t{\gamma^t}r^t$ 。
為了學習策略 $\pi_{\theta}$ ，各種MARL算法被提出。例如，離線策略 Actor-Critic算法 MATD3作為示例方法。具體來說，通過最小化時間差（TD）誤差損失來更新批評器網絡
$\mathcal{L}_c(\phi)=\mathbb{E}_{(s^t,\boldsymbol{o}^t,\boldsymbol{a}^t,r^t,s^{t+1},\boldsymbol{o}^{t+1})\sim\mathcal{D}}\left[\left(y^t-Q(s^t,\boldsymbol{a}^t;\phi)\right)^2\right],\hspace{1cm} (1)$
其中
$y^t=r^t+\gamma\min_{j=1,2}Q(s^{t+1},\pi_1(o_1^{t+1};\theta_1^{\prime})+\epsilon,\ldots,\pi_N(o_N^{t+1};\theta_N^{\prime})+\epsilon;\phi_j),\hspace{1cm} (2)$
其中 $\phi$ 是批評器參數， $\theta$ 是執行策略參數， $\theta^{'}$ 是目標執行策略參數， $\epsilon$ 是截斷高斯噪聲，遵循分布 $\mathsf{clip}(\mathcal{N}(0,\sigma),-c,c)$ 。
策略更新采用確定性策略梯度算法
$\nabla\mathcal{J}(\theta_i)=\mathbb{E}_{(s^t,\boldsymbol{o}^t,\boldsymbol{a}^t,r^t,s^{t+1},\boldsymbol{o}^{t+1})\thicksim\mathcal{D}}\left[\nabla_{\theta_i}\pi_i(o_i^t;\theta_i)\nabla_{a_i}Q(s^t,a_1,\ldots,a_N|_{a_i=\pi_i(o_i^t;\theta_i)};\phi_1)\right].\hspace{1cm} (3)$
軟閾值重參數化（STR） 最初是在模型稀疏化的背景下引入的，STR 是一種非結構化修剪方法，無需預先確定稀疏度水平即可實現顯著性能。具體來說，STR對原始參數W進行如下變換
$\mathcal{S}_g(W,s)=\mathrm{sign}(W)\cdot\mathrm{ReLU}\left(|W|-g(s)\right),\hspace{1cm} (4)$
其中 $s$ 是可學習參數， $\alpha=g(s)$ 作為修剪閾值， $\mathrm{ReLU}(\cdot)=\max(\cdot,0)$ 。
最初的監督學習問題建模為
$\min_{\boldsymbol{W}}\mathcal{L}(\boldsymbol{W};\mathcal{D})\hspace{1cm} (5)$
其中 $;\mathcal{D}$ 作為數據現在轉換為
$\min_{\boldsymbol{W},\boldsymbol{s}}\mathcal{L}(\mathcal{S}_g(\boldsymbol{W},s);\mathcal{D}).\hspace{1cm} (6)$
總體而言，該方法優化了可學習剪枝閾值和模型參數，便于在訓練過程中動態調整到稀疏度水平。
3 用于異構多智能體強化學習的可學習掩碼
在本節中，我們提出使用可學習掩碼作為一種低成本的方法來實現MARL中的網絡異構。如圖2所示，其核心概念是學習一組由不同智能體的多個掩碼補充的共享參數，并指定要共享哪些參數。
在這里插入圖片描述
圖2：萬花筒的整體網絡架構。它為Actor網絡維護帶有N組掩碼 $\left[M_{i}\right]_{i=1}^{N}$ 的一組參數 $\theta_0$ 以及為集成Critic網絡維護帶有K組掩碼 $\left[M_j^c\right]_{j=1}^K$ 的一組參數 $\phi_{0}$ ，其中N是智能體的個數，K是集成網絡中子網絡的數量， $\odot$ 是哈達瑪積。
具體而言，在第3.1節中，我們首先將STR改進為動態部分參數共享方法，解鎖聯合策略網絡在智能體之間表示多種策略的能力。在第3.2節中，我們通過基于掩碼的新正則化項積極促進策略異質性。考慮到掩碼技術可能會過度稀疏網絡，潛在地降低其表示能力，在第3.3節中，我們提出了一種直接的補救措施，根據掩碼的結果周期性地重置參數，這也減輕了首要偏差。最后，在第3.4節中，我們將探討如何在Actor- Critic算法的Critic組件中進一步擴展這種方法，以改進MARL中的值估計并進一步提高性能。
為了清晰起見，我們將提出的萬花筒與MATD3 算法集成在一起，以演示本節中的概念。然而，作為一種通用的部分參數共享技術，我們的方法可以很容易地適應其他MARL算法。我們將其與其他MARL框架的集成放到附錄A.1.2，并將在第4節對它們進行實驗評估。
3.1 自適應部分參數共享
這項工作的核心思想是為不同的智能體學習不同的二進制掩碼 $M_i$ ，以促進差異化策略，最終旨在提高MARL性能。為了實現這一目標，我們將STR技術應用于每個智能體專用的具有不同閾值的策略參數：
$\theta _{i}= \theta _{0}\odot M_{i}\hspace{1cm} (7)$
其中 $\theta _{i}$ 表示智能體 $i$ 的策略參數， $\theta _{0}$ 表示所有智能體共享的一組可學習參數， $M _{i}$ 為每個智能體的可學習掩碼。具體來說，假設 $\theta_0=\begin{bmatrix}\theta_0^{(1)},\ldots,\theta_0^{(N_a)}\end{bmatrix}$ ， $\theta_i=\left[\theta_i^{(1)},\ldots,\theta_i^{(N_a)}\right]$ ， $M_i=\left[m_i^{(1)},\ldots,m_i^{(N_a)}\right]$ ，其中 $N_a$ 是一個智能體網絡的總參數量。與STR保持一致，我們計算 $M_i$ 中的每一個元素 $m_i^{(k)}=\mathbb{1}\left[|\theta_0^{(k)}|>\sigma(s_i^{(k)})\right]$ ,其中 $\sigma(\cdot)$ 為Sigmoid函數。
這種結合的好處總結如下：

保留原MARL學習目標：與剪枝相關文獻中的大多數方法不同，它們主要目的是盡量減少剪枝和未剪枝網絡在權重，損失或激活方面的差異，STR保持最小化特定任務損失的原始目標，與我們提高MARL性能的目標直接一致。
稀疏的靈活性：許多經典的剪枝方法需要預定義每層的稀疏度水平。這樣的需求會使我們的設計復雜化，我們的目標不是獲得極端的稀疏性，而是通過掩碼來促進異構性。STR技術在我們的案例中是理想的，因為它不需要預定義稀疏度水平，允許掩碼的自適應學習。
增強網絡表征能力：利用可學習掩碼進行自適應部分參數共享，提高了網絡的表征能力，超越了傳統的全參數共享。在全參數共享中，智能體的聯合策略參數化表示為 $\pi^{\mathrm{ps}}(\cdot|\theta_{0})\quad=\quad\langle\pi_{1}(\cdot|\theta_{0}),\ldots,\pi_{N}(\cdot|\theta_{0})\rangle$ 相比之下，我們提出的自適應部分參數共享機制將聯合策略參數化表示為 $\pi^\text{Kaleidoscope}{(\cdot|\theta_0,M)}=\langle\pi_1(\cdot|\theta_0\odot M_1),\ldots,\pi_n(\cdot|\theta_0\odot M_N)\rangle$ 。在極端情況下， $M_i$ 中所有的值都為1s，函數集表示為 $\pi^{\text{Kaleidoscope}}(\cdot|\theta_{0},M)$ 退化為 $\pi^{\mathrm{ps}}(\cdot|\theta_{0})$ 。其他情況下，它是由 $\pi^{\mathrm{ps}}(\cdot|\theta_{0})$ 表示的集合的超集。

3.2 策略異質性正則化
雖然獨立學習的掩碼使智能體能夠制定不同的策略，但在沒有特定激勵的情況下，這些策略仍然可能收斂到同質。為此，我們建議通過引入多樣性正則化項來最大化網絡掩碼之間的加權兩兩距離，從而明確鼓勵智能體策略的異質性，該正則化項定義為
$\mathcal{J}^{\mathrm{div}}(s)=\sum_{i=1,\ldots,n}\sum_{j=1,\ldots,n}\|\theta_0\odot(M_i-M_j)\|_1.\hspace{1cm} (8)$
由于M中的指示函數 $\mathbb{1}[\cdot]$ ，這一項本質上不可微。為了克服這一困難，遵循文獻中的既定做法，我們利用代理函數進行梯度近似：
$\frac{\partial\mathcal{J}^\mathrm{div}}{\partial g(s_i)}=-\tanh\left[\frac{\partial\mathcal{J}^\mathrm{div}}{\partial M_i}\right].\hspace{1cm} (9)$
我們在附錄A.1.1中正式提供了Actor的總體訓練目標。
3.3 定期重置
隨著掩碼訓練的進行，我們觀察到每個智能體網絡的稀疏度越來越大，這可能會降低整個網絡的容量。為了解決這個問題，我們提出了一種簡單的方法，以一定的概率ρ周期性地重置在所有 $M_i$ 上一致屏蔽的參數，如圖3a所示。在由t定義的區間內修改reset_interval==0，如果參數索引k滿足 $\forall i,m_i^{(k)}==0$ 我們應用以下重置規則
$\theta_0^{(k)},s_1^{(k)},\ldots,s_N^{(k)}\leftarrow \begin{cases} \text{Reinitialize}[\theta_0^{(k)},s_1^{(k)},\ldots,s_N^{(k)}] & \text{with probability }\rho \\ \theta_0^{(k)},s_1^{(k)},\ldots,s_N^{(k)} & \text{with probability }1-\rho & \end{cases}.\hspace{1cm} (10)$
這種重置機制回收被所有掩碼屏蔽為零的權重，從而防止網絡變得過于稀疏。這種重置機制的一個附帶好處是增強神經可塑性，這有助于緩解強化學習中的首因偏差。與重新初始化整個層導致性能突然下降的方法不同，我們的重置方法選擇性地針對可學習掩模所指示的權重，從而避免了顯著的性能中斷，如第4節所示。
在這里插入圖片描述
圖3：重置機制的說明
3.4 帶有可學習掩碼的批評器集成
在Actor-Critic算法框架中，我們進一步將萬花筒應用于中心批評器，作為實現集成式批評器的有效方法。通過促進動態部分參數共享，萬花筒實現了批評器集合之間的異質性。此外，通過規范批評器函數之間的異質性，我們可以控制集成方差。這一方法將在以后各段加以闡述。

批評器集成的自適應部分參數共享 在標準的MATD3算法中，維護兩個具有獨立參數的批評器以減輕過估計風險。但是，使用單獨的參數通常會導致對數據的利用效率較低。為了解決這個問題，我們提出通過在批評器集合中使用萬花筒參數共享來提高數據利用效率。具體來說，我們維護一組參數 $\phi_{0}$ 和K個掩碼 $\begin{bmatrix}M_j^c\end{bmatrix}_{j=1}^K$ 以區分批評函數，從而產生由K個批評器組成的集成批評器 $[Q(\cdot;\phi_j)]_{j=1}^K$ ，其中 $\phi_j=\phi_0\odot M_j^c$ 。
具體來說，我們通過最小化時間差（TD）誤差損失來更新批評器網絡
$\mathcal{L}_c(\phi_j)=\mathbb{E}_{(s^t,\boldsymbol{a}^t,s_{t+1})\sim\mathcal{D}}\left[\left(y^t-Q(s^t,\boldsymbol{a}^t;\phi_j)\right)^2\right],\hspace{1cm} (11)$
其中
$y^t=r^t+\gamma\min_{j=1,...,K}Q(s^{t+1},\pi_1(o_1^{t+1};\theta_1^{\prime})+\epsilon,...,\pi_n(o_N^{t+1};\theta_N^{\prime})+\epsilon;\phi_j).\hspace{1cm} (12)$
并根據批評器集合的均值估計來更新策略
$\nabla\mathcal{J}(\theta_i)=\mathbb{E}_{s^t\sim\mathcal{D}}\left[\nabla_{\theta_i}\pi_i(o_i^t;\theta_i)\nabla_{a_i}\frac{1}{K}\sum_{j=1}^K\left[Q(s^t,a_1,\ldots,a_N|_{a_i=\pi_i(o_i^t;\theta_i)};\phi_j)\right]\right].\hspace{1cm} (13)$
批評器集合的多樣性正則化 如第3.2節所述，我們還將多樣性正則化應用于批評器掩碼，以防止批評函數崩潰為相同的函數。最大化批評器集合的多樣性正則化表示為
$\mathcal{J}_c^{\mathrm{div}}(s^c)=\sum_{i=1,\ldots,K}\sum_{j=1,\ldots,K}\|\phi_0\odot(M_i^c-M_j^c)\|_1.\hspace{1cm} (14)$
直觀地說，隨著訓練的進展，這個正則項鼓勵了批評掩碼之間的差異性，導致模型估計的不確定性增加。這個過程促進了從過估計到欠估計的逐漸轉變。正如之前的研究所討論的那樣，過估計可以鼓勵探索，在早期訓練階段是有益的，而欠估計可以減輕誤差積累，這在訓練后期是首選的。我們在附錄A.1.1中正式提供了批評器集合的總體訓練目標。
定期重置 為了進一步促進批評器集合之間的多樣性，并抵消掩碼導致的網絡容量減少，我們實現了類似于第3.3節所述的重置機制。特別是，我們按照循環模式依次重新初始化掩碼 $M_{j}^{c}$ ，如圖3b所示。通過這種方式，每個批評函數的掩碼在不同的數據段上進行訓練，從而導致不同的偏差。綜上所述，通過采用萬花筒參數共享和可學習掩碼，我們為實現具有高數據利用效率的批評器集合建立了一種經濟有效的方法。通過增強掩碼之間的區分度，我們巧妙地控制了批評函數之間的差異，從而改善了MARL中的價值估計。

4.實驗結果
在本節中，我們將萬花筒與基于價值的MARL算法QMIX和Actor-Critic MARL算法MATD3集成，并在三個基準任務中的11個場景中對它們進行評估。
表1 在實驗中進行比較的方法。這里的“adaptive”表示共享方案在訓練過程中是否進化。
在這里插入圖片描述
4.1 實驗設置
環境描述 我們在三個基準任務上測試了我們提出的萬花筒：MPE、MaMuJoCo和SMACv2。對于離散任務MPE和SMACv2，我們將萬花筒和基線與QMIX集成并評估性能。對于連續任務MaMuJoCo，我們采用MATD3 。我們對MPE和MaMuJoCo使用了5個隨機種子，對SMACv2使用了3個隨機種子，報告了平均結果，并用陰影區域顯示了95%的置信區間。所選擇的基準任務反映了離散和連續動作空間以及同構和異構智能體類型的混合，詳見附錄A .2。
基線在下文中，我們將我們提出的萬花筒與基線進行比較，如表1所示。對于萬花筒和基線，在具有固定智能體類型（MPE和MaMuJoCo）的場景中，我們為每個智能體分配一個掩碼。對于智能體類型不同的SMACv2，我們為每個智能體類型分配一個掩碼。在可用的情況下，我們使用基線的官方實現；否則，我們將密切關注他們各自論文中的描述，將其集成到QMIX或MATD3中。附錄A.1.3中提供了超參數和進一步的細節。
4.2 結果
性能我們在圖4和圖5中展示了萬花筒和基線的比較性能。總的來說，Kaleidoscope表現出了優越的性能，這歸功于可學習掩碼的靈活性和多樣性正則化的有效性。此外，我們觀察到，除了Ant-v2-4x2場景外，FuPS + ID通常優于NoPS（圖4c）。這種優勢很大程度上是由于FuPS更高的樣本利用效率；單個轉換數據樣本在FuPS + ID中更新模型參數N次，每個智能體一次，而在NoPS中只更新一次。因此，FuPS + ID模型從相同數量的轉換中學習得更快。同樣的, Kaleidoscope受益于這種機制，因為它在智能體之間共享權重，允許一次轉換多次更新模型參數。此外，通過可學習掩碼集成策略異質性，Kaleidoscope實現了不同的智能體行為，如圖8所示的可視化結果。最終，萬花筒有效地平衡了參數共享和多樣性，優于全參數共享和非參數共享方法。
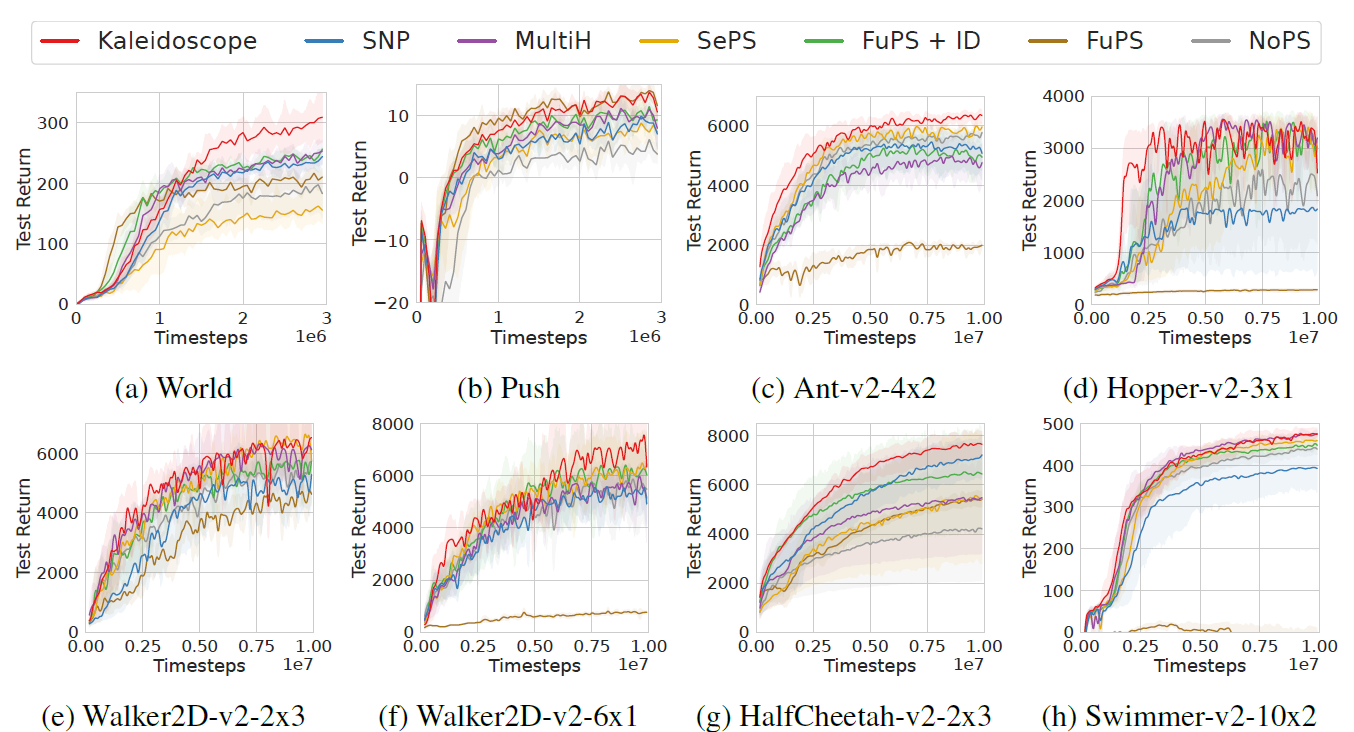
在這里插入圖片描述
圖4：MPE和MaMuJoCo基準任務上與基線的性能比較

圖5：SMACv2基準任務上與基線的性能比較。
成本分析 盡管Kaleidoscope具有優越的性能，但與基線相比，它在測試時并沒有增加計算復雜度。我們報告了萬花筒和表2中基線方法測試時間平均FLOPs的比較。我們看到，由于掩碼技術，萬花筒與基線相比具有更低的FLOPs，因此在部署時具有更快的推理速度。
表2：不同方法的平均FLOPs。此外，我們還進行了實驗來研究口罩設計的影響。首先根據每個場景的FuPS + ID模型對結果進行歸一化，然后對每個環境中的各個場景進行平均。最低成本以粗體突出顯示。
在這里插入圖片描述

消融實驗 我們進行了消融研究，以評估萬花筒中關鍵部件的影響，結果如圖6所示。具體來說，我們比較萬花筒及其三種消融：1)萬花筒 w/o reg，缺少式(8)中使得掩碼可以區分的正則化項。2)萬花筒 w/o reset，不重置參數。3)萬花筒w/o ce ，它不使用萬花筒參數共享在批評器集合中，而是為批評器保留兩個獨立的參數集。結果表明，多樣性正則化對萬花筒的性能貢獻最大。如果沒有正則化，由于每個策略網絡中的參數數量減少，掩碼會降低性能。在需要時，重置主要有助于訓練后期階段的學習，這與先前研究工作的觀察一致。值得注意的是，即使重置，由于掩碼提供的關于重置位置的指導，性能也不會突然下降。當對具有萬花筒參數共享的批評器集合進行消融時，我們觀察到從訓練開始就表現較差。這是因為與萬花筒參數共享的批評器集合使批評器具有更高的數據利用效率，如3.4節所述。
在這里插入圖片描述
圖6：消融實驗
此外，我們還進行了實驗來研究掩碼設計的影響。結果如圖7所示。具體來說，我們比較了原來的萬花筒與兩種不同的掩碼設計選擇：1)萬花筒/神經元掩碼，其中自適應掩碼技術應用于神經元而不是權重。2)帶有固定掩碼的萬花筒，其中掩碼在訓練開始時初始化，并在整個學習過程中保持固定。結果表明，在任何一種設計選擇下，性能都會下降，這表明萬花筒的優越性能源于可學習掩碼對權重的靈活性。
關于超參數分析的更多結果見附錄B.2。
在這里插入圖片描述
圖7：掩碼設計比較
可視化 我們將Kaleidoscope在World上的訓練策略可視化，如圖8a所示。智能體表現出合作的分而治之策略（四個紅色智能體分成兩個團隊并包圍獵物），與圖1中描述的同質策略形成對比。我們進一步檢查了智能體掩碼的區別，并在圖8b中給出了結果。首先，我們觀察到，在訓練結束時，每個智能體都開發了一個獨特的掩碼，這表明不同的掩碼通過選擇性地激活神經網絡權重的不同部分來促進不同的策略。其次，在整個訓練過程中，我們注意到智能體掩碼之間的差異是動態演變的。這一觀察結果證實了萬花筒有效地實現了基于學習進度的智能體之間的動態參數共享，這是由可學習掩模的適應性賦予的。更多的可視化結果見附錄B.3。
在這里插入圖片描述
圖8：World的可視化結果

5.相關工作
參數共享 首先由Tan（1993）提出，參數共享(Foerster et al., 2018；Rashid et al., 2020；Yu et al., 2022)由于其簡單和高樣本效率（Grammel et al., 2020）在MARL算法得到廣泛應用。然而，沒有參數共享的方案通常為策略表示提供更大的靈活性。為了平衡樣本效率和策略表征能力，一些研究致力于尋找有效的部分參數共享方案。值得注意的是，SePS （Christianos et al., 2021）首先根據訓練開始時的轉換對智能體進行聚類，并限制這些聚類內的參數共享。隨后，SNP(Kim and Sung, 2023)利用彩票假設（Su et al., 2020）初始化異構網絡結構，實現部分參數共享。與我們的工作同步，AdaPS （Li et al., 2024）通過提出基于簇的部分參數共享方案將SNP和SePS結合起來。雖然這些方法在某些領域顯示出希望，但它們的性能潛力往往受到訓練早期設置的參數共享方案的靜態性質的限制。我們提出的萬花筒通過動態學習特定的參數共享配置以及MARL策略的開發來區分自己，從而提供增強的訓練靈活性。
MARL中智能體的異構性 為了將智能體異構性納入MARL中，并使智能體之間的行為多樣化，以前的方法已經探索了多樣性和角色等概念。具體來說，基于多樣性的方法旨在通過對比學習技術，增強基于身份、軌跡或信用分配的智能體之間的成對可區分性。同時，基于角色的策略，有時被稱為技能或子任務，采用條件策略通過分配不同的條件來區分智能體。這些條件可能基于智能體身份、局部觀察、局部歷史或聯合歷史。這條線的研究主要集中在模塊設計上，與參數級調整分開進行，與我們的方法是正交的。然而，將這些方法與我們的工作相結合可能會進一步提高性能。
深度強化學習（RL）中的稀疏網絡雖然相對較少，但最近有一些值得注意的嘗試為深度強化學習尋找稀疏網絡。特別是PoPS(Livne和
Cohen, 2020)在訓練后對密集網絡進行修剪，顯著降低了執行時間復雜度。此外，（Yu et al., 2020）在RL領域驗證了彩票假設，即使在極端修剪率下也能產生高性能模型。隨后的研究包括DST （Sokar et al., 2022）、TE-RL* (Graesser et al., 2022)和RLx2 (Tan et al.，2023)采用拓撲進化（TE）技術進一步降低訓練成本。雖然這些開發利用了稀疏訓練技術，這與我們使用的方法類似，但它們的主要重點是減少單智能體設置中的訓練和執行成本。相比之下，我們的工作利用稀疏網絡策略作為增強參數共享技術的手段，旨在提高MARL性能。
6 結論和未來工作
本文提出了一種用于MARL新的自適應部分參數共享機制萬花筒。它利用不同的可學習掩碼來促進網絡異質性，適用于智能體策略和批評器集合。具體來說，萬花筒是建立在三個技術組成部分：STR驅動的可學習掩碼，網絡多樣性正則化和周期性重置機制。當應用于智能體策略網絡時，萬花筒平衡了樣本效率和網絡表示能力。在評論家集合的背景下，它提高了價值估計。通過將我們提出的萬花筒與QMIX和MATD3相結合，我們已經從經驗上證明了它在各種MARL基準測試中的有效性。該研究為開發自適應部分參數共享機制以提高MARL的性能提供了廣闊的前景。對于未來的工作，將萬花筒進一步擴展到其他領域，如離線MARL或元RL，是一個有趣的研究方向。