一、8種常見數據結構

1. 數組(Array)
- 簡介:數組是有序元素的序列,連續內存塊存儲相同類型元素,通過下標直接訪問。數組會為存儲的元素都分配一個下標(索引),此下標是一個自增連續的,數組下標從0開始訪問,
- 核心特點:
- 查詢速度快;隨機訪問時間復雜度為 O(1)。
- 增刪速度慢;插入/刪除元素需移動后續元素,時間復雜度 O(n)。
- 大小固定(靜態數組)或可擴展(動態數組)。
- 典型操作:增、刪、改、查。
- 應用場景:基礎數據批量存儲、矩陣運算、緩存實現。



?
2. 鏈表(Linked List)
- 簡介:鏈表是由一系列節點Node(也可稱元素)組成,數據元素的邏輯順序是通過鏈表的指針地址實現,通常情況下,每個節點包含兩個部分,一個用于存儲元素的數據,名叫數據域,另一個則指向下一個相鄰節點地址的指針,名叫指針域。節點通過指針連接,根據節點指針指向,分為單向鏈表、雙向鏈表和循環鏈表。
- 核心特點:
- 增刪速度塊;動態分配內存,插入/刪除時間復雜度 (O(1))(已知節點位置時)。
- 查詢速度慢;隨機訪問效率低(需從頭遍歷,時間復雜度 (O(n)))。
- 典型操作:頭插、尾插、節點刪除、反轉鏈表。
- 應用場景:實現棧、隊列、LRU緩存、哈希表沖突處理。

?

?單向鏈表新增、刪除元素演示:


3. 棧(Stack)
- 簡介:后進先出(LIFO)的線性結構,僅允許在棧頂操作。
- 核心特點:
- 插入(
push)和刪除(pop)時間復雜度均為 O(1)。 - 空間復雜度 O(n),需避免棧溢出。
- 插入(
- 典型操作:壓棧、彈棧、獲取棧頂元素。
- 應用場景:函數調用棧、表達式求值、括號匹配、回溯算法。

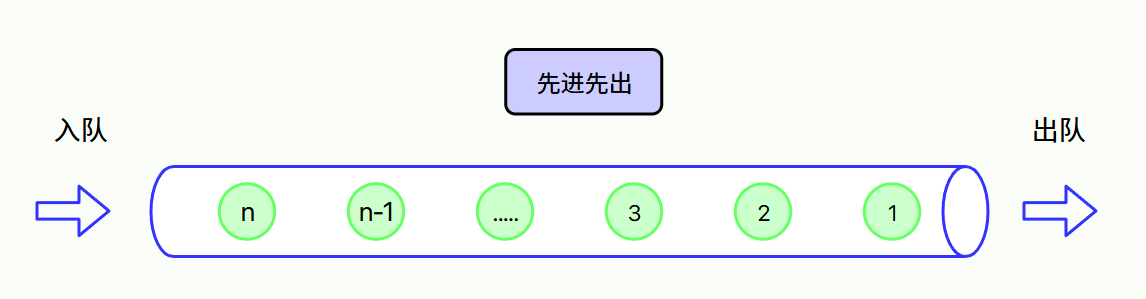
4. 隊列(Queue)
- 簡介:先進先出(FIFO)的線性結構,操作在隊尾(入隊)和隊頭(出隊)。
- 核心特點:
- 普通隊列插入/刪除時間復雜度 O(1)。
- 支持變體:雙端隊列(Deque)、優先隊列(Priority Queue)。
- 典型操作:入隊、出隊、判空、獲取隊頭元素。
- 應用場景:任務調度、BFS算法、消息隊列、滑動窗口。
5. 樹(Tree)
- 簡介:分層數據結構,常見類型包括二叉樹、平衡樹、B/B+樹等。
- 核心特點:
- 二叉樹:每個節點最多兩個子節點。
- 平衡樹(如AVL、紅黑樹):通過旋轉保持高度平衡,保證查詢效率 O(logn)。
- 典型操作:插入、刪除、查找、遍歷(前/中/后序)。
- 應用場景:數據庫索引(B+樹)、文件系統、決策樹算法。

6. 圖(Graph)
- 簡介:由頂點(Vertex)和邊(Edge)構成,分為有向圖與無向圖。
- 有向圖:邊不僅連接兩個頂點,并且具有方向;
- 無向圖:邊僅僅連接兩個頂點,沒有其他含義;
- 核心特點:
- 鄰接矩陣存儲(空間 (O(n^2)))或鄰接表存儲(空間 (O(n+e)))。
- 支持權重圖、稀疏圖、稠密圖等變體。
- 典型操作:遍歷(DFS/BFS)、最短路徑(Dijkstra)、最小生成樹(Prim/Kruskal)。
- 應用場景:社交網絡、路徑規劃、推薦系統、依賴分析。

7. 哈希表(Hash Table)也稱為散列表
- 簡介:基于鍵值對(Key-Value)存儲,通過哈希函數映射位置。散列表其實是數組的一種擴展,由數組演化而來。
- 核心特點:
- 理想情況下查詢/插入/刪除時間復雜度 O(1)。
- 需處理哈希沖突(鏈地址法、開放尋址法)。
- 典型操作:插入、刪除、查找、擴容(Rehashing)。
- 應用場景:字典、緩存(Redis)、唯一性檢查、分布式一致性哈希。

8. 堆(Heap)
- 簡介:堆可以看做是一棵用數組實現的二叉樹,所以它沒有使用父指針或者子指針。堆根據“堆屬性”來排序,“堆屬性”決定了樹中節點的位置。
- 分為大頂堆(父節點值 ≥ 子節點)和小頂堆。
- 核心特點:
- 堆化(Heapify)時間復雜度 O(n)。
- 插入/刪除堆頂元素時間復雜度 O(logn)。
- 典型操作:插入元素(上浮)、刪除堆頂(下沉)、構建堆。
- 應用場景:優先隊列、Top K問題、堆排序、定時任務調度。

總結對比
| 數據結構 | 插入/刪除時間復雜度 | 查詢時間復雜度 | 典型用途 |
|---|---|---|---|
| 數組 | O(n) | O(1) | 快速隨機訪問 |
| 鏈表 | O(1) | O(n) | 動態數據操作 |
| 棧/隊列 | O(1) | O(1) | 受限順序操作 |
| 哈希表 | O(1) | O(1) | 高效鍵值存儲 |
| 堆 | O(logn) | O(1) | 極值優先處理 |
選擇建議:根據場景需求選擇數據結構:
- 需要快速查詢 → 數組、哈希表。
- 高頻插入/刪除 → 鏈表、樹、堆。
- 分層關系 → 樹、圖。
- 順序約束 → 棧、隊列。












:實現暗黑模式主題切換)






