1. 背景與引入
-
正態分布
- 歷史來源:18世紀由高斯(Gauss)在研究測量誤差時提出,后被廣泛應用于自然現象和社會科學的數據建模。
- 重要性:被稱為“鐘形曲線”,是統計學中最核心的分布之一,支撐中心極限定理,解釋為何大量獨立隨機變量的均值趨于穩定。
- 實際問題:人的身高、考試成績、工廠零件尺寸等數據為何大多集中在平均值附近?如何用數學描述這種“中間多、兩頭少”的規律?
- 學習目標:掌握正態分布的核心特征(對稱性、集中趨勢),學會用均值和方差描述數據,并理解其在機器學習中數據預處理(如標準化)和假設檢驗中的作用。
-
冪律分布
- 歷史來源:19世紀帕累托(Pareto)研究財富分布時發現“二八法則”,后被推廣到網絡科學、地震強度、城市人口等領域。
- 重要性:描述“長尾現象”和極端事件的重要性,挑戰傳統統計學對平均值的依賴,在復雜系統分析中不可或缺。
- 實際問題:為何互聯網流量集中在少數網站?為何社交媒體上少數用戶擁有巨量粉絲?如何量化這類“富者愈富”的現象?
- 學習目標:理解冪律分布的標度不變性(無特征尺度),識別數據中的“長尾”形態,并掌握其在推薦系統、風險建模等場景的應用邏輯。
共同鋪墊:
通過對比身高(正態)與財富(冪律)的差異,引出兩種分布對現實建模的本質區別——前者強調均值代表性,后者強調極端值主導性,為后續數學性質和算法設計埋下伏筆。
2. 核心概念與定義
正態分布(Normal Distribution)
-
正式定義:
若隨機變量 X X X的概率密度函數為
f ( x ) = 1 2 π σ e ? ( x ? μ ) 2 2 σ 2 ( ? ∞ < x < ∞ ) , f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}} \quad (-\infty < x < \infty), f(x)=2π?σ1?e?2σ2(x?μ)2?(?∞<x<∞),
則稱 X X X服從參數為 μ \mu μ(均值)和 σ 2 \sigma^2 σ2(方差)的正態分布,記作 X ~ N ( μ , σ 2 ) X \sim \mathcal{N}(\mu, \sigma^2) X~N(μ,σ2)。 -
核心思想:
數據圍繞中心值(均值)對稱分布,越靠近中心的值出現概率越高,極端值極少。
類比:
想象一個沙漏——沙子在中間最集中,兩端逐漸減少;或人群身高分布,大多數人接近平均身高,極高或極矮的人很少。 -
幾何直觀:
- 鐘形曲線:對稱的單峰曲線,均值處最高,兩側對稱衰減。
- 參數意義:
- 均值 μ \mu μ決定曲線的中心位置(如男性平均身高 175cm)。
- 標準差 σ \sigma σ決定曲線的“胖瘦”(如學生考試成績標準差大,曲線矮胖;標準差小,曲線尖瘦)。
冪律分布(Power Law Distribution)
-
正式定義:
若隨機變量 X X X的概率密度函數滿足
f ( x ) = C x ? α ( x ≥ x min ? , α > 1 ) , f(x) = Cx^{-\alpha} \quad (x \ge x_{\min}, \alpha > 1), f(x)=Cx?α(x≥xmin?,α>1),
其中 C C C為歸一化常數,則稱 X X X服從冪律分布,參數 α \alpha α為冪律指數。 -
核心思想:
小概率事件的累積效應顯著,極端值可能出現且影響巨大,數據呈現“長尾”特征。
類比:
社交網絡中,少數“網紅”擁有上億粉絲(極端值),而大多數人只有幾十個好友(平凡值),但所有平凡值的總和仍不可忽視。 -
幾何直觀:
- 長尾曲線:橫軸表示取值(如財富),縱軸表示概率,曲線在右側拖出極長的尾部(如極少數人占據社會大部分財富)。
- 雙對數圖特征:在雙對數坐標系中,冪律分布表現為一條直線,斜率與 α \alpha α相關(如斜率越陡,尾部越薄)。
關鍵對比鋪墊:
- 正態分布的鐘形曲線“收尾快”(極端值概率趨近于 0),冪律分布的長尾“收尾慢”(極端值仍有可觀概率)。
- 正態分布的均值和方差有限,冪律分布當 α ≤ 3 \alpha \leq 3 α≤3時方差無窮大,極端事件主導統計性質。
3. 拆解與解讀
正態分布(Normal Distribution)
-
公式拆解:
f ( x ) = 1 2 π σ e ? ( x ? μ ) 2 2 σ 2 f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}} f(x)=2π?σ1?e?2σ2(x?μ)2?
分解為三部分:- 系數項: 1 2 π σ \frac{1}{\sqrt{2\pi}\sigma} 2π?σ1?—— 歸一化常數,確保概率密度積分總和為1。
- 指數項: e ? ( x ? μ ) 2 2 σ 2 e^{-\frac{(x-\mu)^2}{2\sigma^2}} e?2σ2(x?μ)2?—— 決定曲線形狀的核心部分。
- 參數: μ \mu μ(均值)、 σ \sigma σ(標準差)。
-
逐項解讀:
(1) 系數項:- 類比:類似“調整音量”——無論曲線形狀如何,必須保證總面積(概率總和)為1。
- 數學意義: 2 π \sqrt{2\pi} 2π?是高斯積分的結果( ∫ ? ∞ ∞ e ? x 2 d x = π \int_{-\infty}^\infty e^{-x^2} dx = \sqrt{\pi} ∫?∞∞?e?x2dx=π?),乘以 σ \sigma σ后反映分布的寬窄。
(2) 指數項:
- 結構: ? ( x ? μ ) 2 2 σ 2 -\frac{(x-\mu)^2}{2\sigma^2} ?2σ2(x?μ)2?是一個“懲罰項”,當 x x x遠離均值 μ \mu μ時,指數快速衰減。
- 生活化解釋:
- ( x ? μ ) 2 (x-\mu)^2 (x?μ)2:像“距離中心的平方代價”——離中心越遠,代價越大。- 分母 2 σ 2 2\sigma^2 2σ2:類似“調節放大鏡倍數”—— σ \sigma σ越大,衰減越慢(曲線越胖)。
- 幾何意義:形成鐘形曲線的對稱下降趨勢。
(3) 參數 μ \mu μ與 σ \sigma σ:
- μ \mu μ:控制“中心位置”(如男性平均身高175cm vs 女性162cm)。
- σ \sigma σ:控制“分散程度”(如考試難度低時成績 σ \sigma σ小,難度高時 σ \sigma σ大)。 -
推導邏輯:
從中心極限定理出發:獨立同分布的隨機變量之和趨向正態分布(即使原分布非正態)。
例如:拋100次硬幣的正面次數服從近似正態分布,均值50,標準差5。
冪律分布(Power Law Distribution)
-
公式拆解:
f ( x ) = C x ? α ( x ≥ x min ? ) f(x) = Cx^{-\alpha} \quad (x \ge x_{\min}) f(x)=Cx?α(x≥xmin?)
分解為三部分:- 歸一化常數 C C C:確保概率密度積分總和為1。
- 冪律核 x ? α x^{-\alpha} x?α:決定長尾特性的核心。
- 參數: α \alpha α(冪律指數)、 x min ? x_{\min} xmin?(最小取值閾值)。
-
逐項解讀:
(1) 冪律核 x ? α x^{-\alpha} x?α:- 結構:反比例函數的推廣,指數 α \alpha α決定衰減速率。
- 生活化解釋:
- α = 2 \alpha=2 α=2:若 x x x翻倍,概率密度降至原來的 1 / 4 1/4 1/4(如收入翻倍,人數減少到1/4)。
- α \alpha α越小,尾部越“重”(極端值越多)。 - 幾何意義:在雙對數坐標系中, log ? f ( x ) = log ? C ? α log ? x \log f(x) = \log C - \alpha \log x logf(x)=logC?αlogx為直線,斜率 ? α -\alpha ?α。
(2) 歸一化常數 C C C:
- 推導:通過積分 ∫ x min ? ∞ C x ? α d x = 1 \int_{x_{\min}}^\infty Cx^{-\alpha} dx = 1 ∫xmin?∞?Cx?αdx=1解得:
KaTeX parse error: Expected 'EOF', got '}' at position 49: …-(\alpha - 1)}}}?
類比:類似“按比例縮放蛋糕”——無論 α \alpha α如何變化,總概率必須為1。
(3) 參數 α \alpha α與 x min ? x_{\min} xmin?:
- α \alpha α:決定分布形態——
- α > 3 \alpha > 3 α>3:方差有限(尾部較薄)。
- 1 < α ≤ 3 1 < \alpha \leq 3 1<α≤3:方差無限(極端事件主導)。
- x min ? x_{\min} xmin?:過濾“平凡值”,僅關注顯著事件(如研究地震強度時忽略小震)。 -
長尾效應推導:
計算累積概率 P ( X ≥ x ) P(X \geq x) P(X≥x):
P ( X ≥ x ) = ∫ x ∞ C x ? α d x ∝ x ? ( α ? 1 ) P(X \geq x) = \int_x^\infty Cx^{-\alpha} dx \propto x^{-(\alpha - 1)} P(X≥x)=∫x∞?Cx?αdx∝x?(α?1)
例如:若 α = 2 \alpha=2 α=2,收入超過100萬的概率是10萬的 1 / 10 1/10 1/10,但極端值仍存在(如億萬富翁)。
關鍵對比總結
- 形狀差異:
- 正態分布:鐘形(快速衰減,極端值稀有)。
- 冪律分布:長尾(緩慢衰減,極端值顯著)。
- 參數作用:
- 正態分布: μ \mu μ決定中心, σ \sigma σ決定胖瘦。
- 冪律分布: α \alpha α決定尾部厚度, x min ? x_{\min} xmin?設定起點。
- 現實意義:
- 正態分布:適用于獨立隨機過程(如身高、測量誤差)。
- 冪律分布:適用于復雜系統(如社交網絡、金融市場)。
4. 幾何意義與圖形化展示
正態分布(Normal Distribution)
幾何意義
- 鐘形曲線:對稱分布,峰值位于均值 μ \mu μ,標準差 μ ± σ \mu \pm \sigma μ±σ包含約68%的數據。
- 參數影響:
- μ \mu μ決定中心位置(平移曲線)。
- σ \sigma σ決定曲線胖瘦( σ \sigma σ越大,曲線越寬)。 - 極端值稀有性: μ ± 3 σ \mu \pm 3\sigma μ±3σ以外區域概率極低(約0.3%)。
代碼實現
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm# 參數設定
mu, sigma = 0, 1 # 均值和標準差
x = np.linspace(-5, 5, 1000)# 計算概率密度
y = norm.pdf(x, mu, sigma)# 繪圖
plt.figure(figsize=(8, 5))
plt.plot(x, y, label=f"μ={mu}, σ={sigma}", color='blue')
plt.fill_between(x, y, where=(x >= mu - sigma) & (x <= mu + sigma), color='blue', alpha=0.2, label=r"±1σ (68%)")
plt.fill_between(x, y, where=(x >= mu - 2*sigma) & (x <= mu + 2*sigma), color='green', alpha=0.1, label=r"±2σ (95%)")
plt.title("Figure-1: 正態分布的幾何意義")
plt.xlabel("x")
plt.ylabel("概率密度")
plt.legend()
plt.grid(True)
plt.show()

圖形解讀
- Figure-1:
- 曲線對稱性:左右兩側嚴格對稱。
- 陰影區域:標注 μ ± σ \mu \pm \sigma μ±σ和 μ ± 2 σ \mu \pm 2\sigma μ±2σ的概率覆蓋范圍。
- 極端值區域: x > 3 x > 3 x>3或 x < ? 3 x < -3 x<?3的概率密度接近零。
冪律分布(Power Law Distribution)
幾何意義
- 長尾特性:小概率事件占比顯著,無明確邊界(如少數人擁有巨量財富)。
- 標度不變性:雙對數坐標下為直線, log ? f ( x ) = ? α log ? x + 常數 \log f(x) = -\alpha \log x + \text{常數} logf(x)=?αlogx+常數。
- 極端值主導: α \alpha α較小時,尾部貢獻主要概率質量。
代碼實現
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import powerlaw# 參數設定
alpha = 2.5
x_min = 1
x = np.linspace(x_min, 100, 1000)# 計算概率密度
y = powerlaw.pdf(x, alpha, scale=x_min)# 繪圖(普通坐標)
plt.figure(figsize=(8, 5))
plt.plot(x, y, label=f"α={alpha}", color='red')
plt.fill_between(x, y, where=(x >= 50), color='red', alpha=0.1, label=r"x ≥ 50 的長尾區域")
plt.title("Figure-2: 冪律分布在普通坐標下的長尾")
plt.xlabel("x")
plt.ylabel("概率密度")
plt.legend()
plt.grid(True)
plt.show()# 雙對數坐標驗證標度不變性
plt.figure(figsize=(8, 5))
plt.loglog(x, y, label=f"α={alpha}", color='red')
plt.title("Figure-3: 冪律分布的雙對數坐標驗證")
plt.xlabel("log(x)")
plt.ylabel("log(f(x))")
plt.legend()
plt.grid(True)
plt.show()

圖形解讀
- Figure-2:
- 曲線陡峭下降,但右側陰影區域(長尾)仍占顯著面積。
- 小 x x x值概率密度高,大 x x x值概率密度衰減緩慢。
- Figure-3:
- 雙對數坐標下為直線,斜率 ? α -\alpha ?α,驗證標度不變性。
- 直線截距反映歸一化常數 C C C。
關鍵對比總結
| 特性 | 正態分布 | 冪律分布 |
|---|---|---|
| 坐標系 | 普通坐標下鐘形曲線 | 普通坐標下陡峭,雙對數坐標下為直線 |
| 極端值 | 稀有( μ ± 3 σ \mu \pm 3\sigma μ±3σ外概率≈0.3%) | 常見(長尾區域概率不可忽略) |
| 參數作用 | μ \mu μ決定中心, σ \sigma σ決定寬度 | α \alpha α決定尾部厚度, x min ? x_{\min} xmin?設定起點 |
| 現實意義 | 自然現象(身高、溫度) | 社會與復雜系統(財富、網絡流量) |
通過圖形對比,可直觀理解正態分布適用于獨立隨機過程,而冪律分布揭示復雜系統中“富者愈富”和極端事件的重要性。
5. 常見形式與變換
正態分布(Normal Distribution)
常見形式與等價變換
-
標準正態分布(Standard Normal Distribution)
- 定義: μ = 0 , σ = 1 \mu = 0, \sigma = 1 μ=0,σ=1,記為 Z ~ N ( 0 , 1 ) Z \sim \mathcal{N}(0, 1) Z~N(0,1)。
- 用途:簡化計算(如查標準正態表),數據標準化(Z-score)。
- 變換邏輯:任意正態分布 X ~ N ( μ , σ 2 ) X \sim \mathcal{N}(\mu, \sigma^2) X~N(μ,σ2)可通過 Z = X ? μ σ Z = \frac{X - \mu}{\sigma} Z=σX?μ?轉換。
-
多維正態分布(Multivariate Normal Distribution)
- 定義:
f ( x ) = 1 ( 2 π ) d / 2 ∣ Σ ∣ 1 / 2 e ? 1 2 ( x ? μ ) T Σ ? 1 ( x ? μ ) f(\mathbf{x}) = \frac{1}{(2\pi)^{d/2} |\Sigma|^{1/2}} e^{-\frac{1}{2} (\mathbf{x} - \boldsymbol{\mu})^T \Sigma^{-1} (\mathbf{x} - \boldsymbol{\mu})} f(x)=(2π)d/2∣Σ∣1/21?e?21?(x?μ)TΣ?1(x?μ)
其中 μ \boldsymbol{\mu} μ為均值向量, Σ \Sigma Σ為協方差矩陣。 - 用途:多變量建模(如金融資產收益率、圖像特征向量)。
- 變換邏輯:單變量正態分布的高維推廣,協方差矩陣捕捉變量間相關性。
- 定義:
-
截斷正態分布(Truncated Normal Distribution)
- 定義:限制在區間 [ a , b ] [a, b] [a,b]內的正態分布。
- 用途:有界數據(如考試分數、物理量測量范圍)。
- 變換邏輯:原分布乘以歸一化因子 1 Φ ( b ) ? Φ ( a ) \frac{1}{\Phi(b) - \Phi(a)} Φ(b)?Φ(a)1?,其中 Φ \Phi Φ為累積分布函數。
代碼實現與圖形對比
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm, multivariate_normal# 標準正態分布 vs 截斷正態分布
x = np.linspace(-5, 5, 1000)
y_std = norm.pdf(x, 0, 1)
y_trunc = norm.pdf(x, 0, 1) / (norm.cdf(2) - norm.cdf(-2)) # 截斷范圍[-2, 2]plt.figure(figsize=(8, 4))
plt.plot(x, y_std, label="標準正態分布", color='blue')
plt.plot(x, y_trunc, label="截斷正態分布 [-2, 2]", color='orange', linestyle='--')
plt.title("Figure-1: 標準與截斷正態分布對比")
plt.legend()
plt.grid(True)
plt.show()# 多維正態分布(二維示例)
mean = [0, 0]
cov = [[1, 0.5], [0.5, 1]] # 協方差矩陣
x, y = np.mgrid[-3:3:.05, -3:3:.05]
pos = np.dstack((x, y))
rv = multivariate_normal(mean, cov)
z = rv.pdf(pos)plt.figure(figsize=(6, 5))
plt.contourf(x, y, z, cmap='viridis', levels=20)
plt.colorbar(label='概率密度')
plt.title("Figure-2: 二維正態分布等高線圖")
plt.xlabel("X1")
plt.ylabel("X2")
plt.show()


圖形解讀
- Figure-1:
- 標準正態分布曲線對稱且全域存在概率密度。
- 截斷分布在 [ ? 2 , 2 ] [-2, 2] [?2,2]外概率為零,內部密度被拉高(歸一化)。
- Figure-2:
- 等高線橢圓反映變量間正相關(協方差 0.5),軸對齊時協方差為零。
冪律分布(Power Law Distribution)
常見形式與等價變換
-
離散 vs 連續冪律分布
- 離散形式:如 Zipf 定律(詞頻排名 f ( r ) ∝ r ? α f(r) \propto r^{-\alpha} f(r)∝r?α)。
- 連續形式:如帕累托分布( f ( x ) = C x ? α f(x) = Cx^{-\alpha} f(x)=Cx?α)。
- 聯系:離散形式是連續形式的采樣版本,常用于計數數據(如網頁訪問次數)。
-
累積分布函數(CCDF)形式
- 定義:
P ( X ≥ x ) = ∫ x ∞ f ( x ′ ) d x ′ ∝ x ? ( α ? 1 ) P(X \geq x) = \int_x^\infty f(x') dx' \propto x^{-(\alpha - 1)} P(X≥x)=∫x∞?f(x′)dx′∝x?(α?1) - 用途:實證分析中更易觀察長尾特性(如財富分布)。
- 變換邏輯:概率密度函數積分后斜率從 ? α -\alpha ?α變為 ? ( α ? 1 ) -(\alpha - 1) ?(α?1)。
- 定義:
-
廣義冪律分布(Exponential Cutoff)
- 定義:
f ( x ) = C x ? α e ? λ x f(x) = Cx^{-\alpha} e^{-\lambda x} f(x)=Cx?αe?λx - 用途:有限系統中截斷極端值(如地震強度上限)。
- 變換邏輯:指數項 e ? λ x e^{-\lambda x} e?λx在大 x x x時抑制增長。
- 定義:
代碼實現與圖形對比
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import powerlaw# 離散 vs 連續冪律分布(連續帕累托)
x_cont = np.linspace(1, 100, 1000)
y_cont = powerlaw.pdf(x_cont, a=2.5, scale=1)x_disc = np.arange(1, 101)
y_disc = x_disc**-2.5
y_disc /= y_disc.sum() # 歸一化plt.figure(figsize=(8, 4))
plt.plot(x_cont, y_cont, label="連續冪律(帕累托)", color='blue')
plt.stem(x_disc, y_disc, linefmt='r--', markerfmt='ro', basefmt='none', label="離散冪律(Zipf)", use_line_collection=True)
plt.title("Figure-3: 離散與連續冪律分布對比")
plt.xscale('log')
plt.yscale('log')
plt.legend()
plt.grid(True)
plt.show()# CCDF vs PDF 對比
y_ccdf = 1 - powerlaw.cdf(x_cont, a=2.5, scale=1)plt.figure(figsize=(8, 4))
plt.plot(x_cont, y_cont, label="PDF", color='blue')
plt.plot(x_cont, y_ccdf, label="CCDF", color='green', linestyle='--')
plt.title("Figure-4: 冪律分布的PDF與CCDF對比")
plt.xscale('log')
plt.yscale('log')
plt.legend()
plt.grid(True)
plt.show()


圖形解讀
- Figure-3:
- 連續曲線平滑,離散點呈階梯狀(符合計數數據特性)。
- 雙對數坐標下均為直線,但離散形式因歸一化略有偏移。
- Figure-4:
- PDF 斜率 ? 2.5 -2.5 ?2.5,CCDF 斜率 ? 1.5 -1.5 ?1.5,驗證積分關系。
- CCDF 在尾部更陡峭,凸顯極端事件概率衰減速度。
關鍵對比總結
| 形式 | 正態分布 | 冪律分布 |
|---|---|---|
| 標準形式 | N ( μ , σ 2 ) \mathcal{N}(\mu, \sigma^2) N(μ,σ2) | f ( x ) = C x ? α f(x) = Cx^{-\alpha} f(x)=Cx?α |
| 變換核心 | 平移( μ \mu μ)、縮放( σ \sigma σ) | 指數調整( α \alpha α)、截斷( x min ? x_{\min} xmin?) |
| 圖形特性 | 鐘形曲線,雙側快速衰減 | 長尾,雙對數坐標下為直線 |
| 適用場景 | 獨立隨機過程(如身高、誤差) | 復雜系統(如網絡、金融) |
通過形式變換,可靈活應對不同數據特性(如多維性、離散性、有限性),同時保持分布的核心規律(正態的集中性、冪律的長尾性)。
6. 實際應用場景
正態分布(Normal Distribution)
應用場景 1:工業質量控制(零件尺寸檢測)
-
問題描述:工廠生產某零件,設計長度為 100mm,標準差 2mm。如何設定合格范圍(如 95% 置信區間)并檢測異常批次?
-
解決步驟:
- 數據采集:測量一批次零件長度。
- 假設檢驗:驗證數據是否符合正態分布(如 Q-Q 圖)。
- 計算控制限:
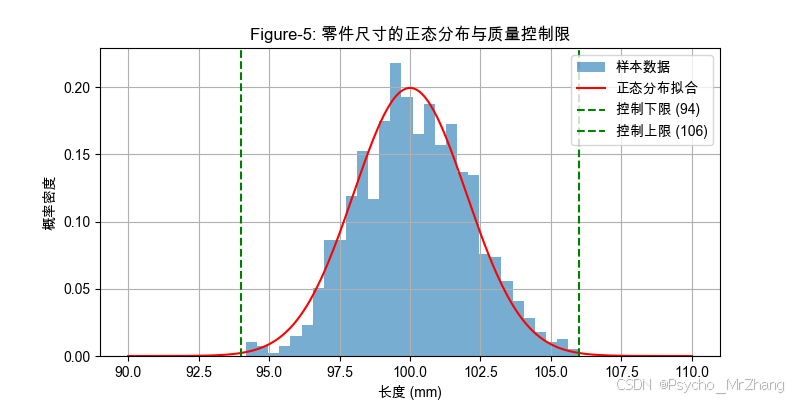
下限 = μ ? 3 σ = 100 ? 6 = 94 , 上限 = μ + 3 σ = 106 \text{下限} = \mu - 3\sigma = 100 - 6 = 94, \quad \text{上限} = \mu + 3\sigma = 106 下限=μ?3σ=100?6=94,上限=μ+3σ=106 - 異常檢測:若零件長度超出 [94, 106],判定為不合格。
- 動態監控:繪制控制圖(Control Chart),實時追蹤生產穩定性。
-
代碼實現:
import matplotlib.pyplot as plt import numpy as np from scipy.stats import norm# 模擬數據 mu, sigma = 100, 2 data = np.random.normal(mu, sigma, 1000) x = np.linspace(90, 110, 1000) y = norm.pdf(x, mu, sigma)# 繪圖:直方圖 + 控制限 plt.figure(figsize=(8, 4)) plt.hist(data, bins=30, density=True, alpha=0.6, label="樣本數據") plt.plot(x, y, 'r-', label="正態分布擬合") plt.axvline(mu - 3*sigma, color='g', linestyle='--', label="控制下限 (94)") plt.axvline(mu + 3*sigma, color='g', linestyle='--', label="控制上限 (106)") plt.title("Figure-5: 零件尺寸的正態分布與質量控制限") plt.xlabel("長度 (mm)") plt.ylabel("概率密度") plt.legend() plt.grid(True) plt.show()
應用場景 2:金融風險評估(VaR 計算)
- 問題描述:估算某股票組合未來一天的 95% 置信水平下的最大虧損(Value at Risk, VaR)。
- 解決步驟:
- 數據準備:收集歷史收益率數據。
- 參數估計:計算均值 μ \mu μ和標準差 σ \sigma σ。
- VaR 計算:
VaR 95 % = μ ? z 0.95 ? σ ( z 0.95 = 1.645 ) \text{VaR}_{95\%} = \mu - z_{0.95} \cdot \sigma \quad (z_{0.95} = 1.645) VaR95%?=μ?z0.95??σ(z0.95?=1.645) - 結果解讀:置信水平下最大預期虧損。
- 注意事項:實際金融數據常存在“肥尾”,需結合歷史模擬法或蒙特卡洛方法修正。
冪律分布(Power Law Distribution)
應用場景 1:社交媒體影響力分析
-
問題描述:識別社交平臺上的關鍵意見領袖(KOL),并量化長尾效應。
-
解決步驟:
- 數據采集:統計用戶粉絲數或轉發量。
- 分布擬合:用冪律模型 P ( x ) ∝ x ? α P(x) \propto x^{-\alpha} P(x)∝x?α擬合數據。
- 參數估計:通過極大似然法估算 α \alpha α。
- KOL 判定:設定閾值 x min ? x_{\min} xmin?,篩選頭部高影響力用戶。
- 長尾價值:計算長尾部分(如尾部 80% 用戶)的總影響力占比。
-
代碼實現:
import matplotlib.pyplot as plt import numpy as np from scipy.stats import powerlaw# 模擬數據(粉絲數) alpha = 2.2 x_min = 100 data = powerlaw.rvs(alpha, scale=x_min, size=10000) data = np.sort(data)[::-1] # 按降序排列# 雙對數坐標繪圖 plt.figure(figsize=(8, 4)) plt.loglog(data, np.arange(1, len(data)+1)/len(data), 'b.', label="用戶粉絲排名") plt.title("Figure-6: 社交媒體粉絲數的冪律分布(雙對數坐標)") plt.xlabel("粉絲數 (log)") plt.ylabel("累積概率 (log)") plt.grid(True) plt.legend() plt.show()

應用場景 2:推薦系統中的長尾商品優化
- 問題描述:電商平臺如何平衡熱門商品(頭部)與冷門商品(長尾)的推薦策略?
- 解決步驟:
- 數據建模:分析商品銷量分布,驗證冪律特性(如 α ≈ 1.5 \alpha \approx 1.5 α≈1.5)。
- 策略制定:
- 頭部商品:采用協同過濾強化推薦。
- 長尾商品:基于內容特征或多樣性算法提升曝光。
- 效果評估:通過 A/B 測試比較不同策略的 GMV(總成交額)提升。
- 關鍵價值:長尾商品總銷量占比可能超過頭部(如亞馬遜圖書銷售),需針對性優化。
關鍵對比總結
| 場景 | 正態分布應用 | 冪律分布應用 |
|---|---|---|
| 核心邏輯 | 集中趨勢 + 對稱性 | 長尾效應 + 標度不變性 |
| 典型問題 | 質量控制、風險評估 | 社交影響力分析、推薦系統優化 |
| 參數作用 | μ \mu μ決定中心, σ \sigma σ決定閾值 | α \alpha α決定頭部集中度, x min ? x_{\min} xmin?過濾噪聲 |
| 圖形特征 | 鐘形曲線 + 控制限 | 雙對數直線 + 長尾占比計算 |
通過實際案例可見:
- 正態分布適用于獨立隨機過程驅動的穩定系統(如工業生產、金融風險)。
- 冪律分布揭示復雜系統中“強者恒強”與“長尾價值”的共存規律(如社交網絡、電商生態)。
7. Python 代碼實現
正態分布(Normal Distribution)
代碼 1:生成正態分布數據并繪制概率密度曲線
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm# 參數設置
mu, sigma = 0, 1 # 均值和標準差
sample_size = 1000 # 樣本量# 生成數據
data = np.random.normal(mu, sigma, sample_size)# 概率密度計算
x = np.linspace(-5, 5, 1000)
pdf = norm.pdf(x, mu, sigma)# 繪圖
plt.figure(figsize=(8, 4))
plt.hist(data, bins=30, density=True, alpha=0.6, label="樣本直方圖")
plt.plot(x, pdf, 'r-', label="理論PDF")
plt.title("Figure-1: 正態分布概率密度曲線")
plt.xlabel("x")
plt.ylabel("概率密度")
plt.legend()
plt.grid(True)
plt.show()
作用:
- 輸入:均值
mu、標準差sigma、樣本量sample_size。 - 輸出:生成的樣本數據及理論概率密度曲線。
- 關鍵點:直方圖顯示樣本分布,紅色曲線為理論密度。
代碼 2:參數估計與假設檢驗
from scipy.stats import norm, kstest# 參數估計
estimated_mu, estimated_sigma = norm.fit(data)
print(f"估計均值: {estimated_mu:.2f}, 估計標準差: {estimated_sigma:.2f}")# Kolmogorov-Smirnov 檢驗
ks_stat, p_value = kstest(data, 'norm', args=(mu, sigma))
print(f"K-S檢驗p值: {p_value:.4f}")
作用:
- 輸入:樣本數據
data。 - 輸出:估計的均值和標準差,以及K-S檢驗的p值(判斷是否符合正態分布)。
- 關鍵點:p值 > 0.05 表示無法拒絕正態分布假設。
冪律分布(Power Law Distribution)
代碼 3:生成冪律分布數據并繪制雙對數曲線
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import powerlaw# 參數設置
alpha = 2.5 # 冪律指數
x_min = 1 # 最小值閾值
sample_size = 1000 # 樣本量# 生成數據
data = powerlaw.rvs(alpha, scale=x_min, size=sample_size)# 排序與累積概率計算
sorted_data = np.sort(data)[::-1] # 降序排列
ccdf = np.arange(1, len(sorted_data)+1) / len(sorted_data)# 雙對數坐標繪圖
plt.figure(figsize=(8, 4))
plt.loglog(sorted_data, ccdf, 'b.', label="CCDF")
plt.title("Figure-2: 冪律分布的雙對數坐標驗證")
plt.xlabel("x (log)")
plt.ylabel("P(X ≥ x) (log)")
plt.grid(True)
plt.legend()
plt.show()
作用:
- 輸入:冪律指數
alpha、最小值x_min、樣本量sample_size。 - 輸出:生成的樣本數據及其累積分布函數(CCDF)在雙對數坐標下的直線。
- 關鍵點:直線斜率反映冪律指數
alpha。
代碼 4:參數估計與擬合優度檢驗
from scipy.stats import powerlaw# 參數估計
params = powerlaw.fit(data, floc=0) # 固定位置參數為0
estimated_alpha, loc, scale = params
print(f"估計冪律指數: {estimated_alpha:.2f}")# 擬合優度檢驗(通過視覺判斷直線性)
作用:
- 輸入:樣本數據
data。 - 輸出:估計的冪律指數
alpha。 - 關鍵點:
powerlaw.fit返回參數(alpha, loc, scale),需固定loc=0以避免偏移。
關鍵對比總結
| 功能 | 正態分布代碼 | 冪律分布代碼 |
|---|---|---|
| 數據生成 | np.random.normal(mu, sigma, size) | powerlaw.rvs(alpha, scale=x_min, size) |
| 參數估計 | norm.fit(data) | powerlaw.fit(data, floc=0) |
| 可視化重點 | 鐘形曲線與直方圖對比 | 雙對數坐標下的直線性驗證 |
| 檢驗方法 | K-S檢驗(正態性) | 直觀判斷直線性(冪律性) |
通過代碼可直接驗證理論分布特性,并應用于實際數據分析(如金融風險評估、社交網絡分析)。
8. 總結與拓展
核心知識點總結
正態分布(Normal Distribution)
- 核心特征:
- 對稱鐘形曲線,由均值 μ \mu μ和標準差 σ \sigma σ完全定義。
- 中心極限定理支撐其在獨立隨機變量中的普適性。
- 關鍵性質:
- μ ± σ \mu \pm \sigma μ±σ覆蓋約68%數據, μ ± 3 σ \mu \pm 3\sigma μ±3σ外為稀有事件。- 適用于穩定系統(如工業質量控制、金融風險評估)。
冪律分布(Power Law Distribution)
- 核心特征:
- 長尾特性,無特征尺度(標度不變性),由指數 α \alpha α決定尾部厚度。
- 極端值主導現象(如“二八法則”、社交網絡影響力)。
- 關鍵性質:
- 雙對數坐標下為直線,斜率 ? α -\alpha ?α。
- 方差可能無限(當 α ≤ 3 \alpha \leq 3 α≤3時)。
- 適用于復雜系統(如推薦系統、城市人口建模)。
關鍵對比
| 特性 | 正態分布 | 冪律分布 |
|---|---|---|
| 數據形態 | 集中對稱,尾部快速衰減 | 長尾,極端值顯著 |
| 參數作用 | μ \mu μ定中心, σ \sigma σ定胖瘦 | α \alpha α定尾部厚度, x min ? x_{\min} xmin?過濾噪聲 |
| 適用場景 | 獨立隨機過程(如身高、誤差) | 復雜系統(如網絡、金融) |
進一步學習方向
-
廣義分布與混合模型
- 正態分布延伸:
- 多元正態分布(協方差矩陣分析)、t分布(小樣本統計)、混合高斯模型(聚類分析)。
- 冪律分布延伸:
- 穩定分布(α-Stable Distribution,含正態分布為特例)、分形理論(自相似性)。
- 正態分布延伸:
-
復雜系統建模
- 網絡科學:無標度網絡(Barabási-Albert 模型)的冪律度分布。
- 金融工程:極值理論(EVT)量化尾部風險,替代正態假設下的風險價值(VaR)。
- 機器學習:
- 數據預處理:正態化(Box-Cox變換) vs 長尾修正(對數變換)。
- 異常檢測:基于正態分布的3σ準則 vs 基于冪律的尾部閾值篩選。
-
深度學習與分布假設
- 正態分布的應用:
- 變分自編碼器(VAE)的隱空間正態化約束。
- 批歸一化(BatchNorm)依賴數據近似正態分布。
- 冪律分布的挑戰:
- 長尾標簽問題(如推薦系統的冷啟動)。
- 圖神經網絡(GNN)中節點度分布的冪律特性處理。
- 正態分布的應用:
開放性思考問題
-
正態分布的局限性
- 若數據真實分布嚴重偏離正態(如存在多峰性或強偏態),傳統基于均值和方差的方法會失效嗎?如何改進?
-
冪律分布的生成機制
- “富者愈富”是冪律分布的唯一成因嗎?是否存在其他動態過程(如優先連接、自組織臨界)導致長尾現象?
-
現實世界的混合分布
- 許多數據可能同時包含正態和冪律特性(如用戶活躍度:中間集中,頭部超活躍)。如何設計混合模型更精準建模?
-
分布假設對算法的影響
- 在強化學習中,策略梯度方法假設動作空間服從正態分布,這對探索長尾策略空間有何限制?
通過系統掌握正態分布與冪律分布的數學本質、應用場景及代碼實現,可為后續深入研究概率建模、復雜系統分析及高級機器學習算法奠定堅實基礎。
9. 練習與反饋
練習題
基礎題(概念與計算)
-
正態分布參數意義
- 設某公司員工年薪服從正態分布 N ( 60 , 1 0 2 ) \mathcal{N}(60, 10^2) N(60,102)(單位:萬元)。
- (a)計算年薪在 50-70 萬元之間的概率。
- (b)若標準差變為 5,概率如何變化?
- 設某公司員工年薪服從正態分布 N ( 60 , 1 0 2 ) \mathcal{N}(60, 10^2) N(60,102)(單位:萬元)。
-
冪律分布的標度不變性
- 已知某網站訪問量服從冪律分布 f ( x ) = C x ? α f(x) = Cx^{-\alpha} f(x)=Cx?α,其中 α = 2 \alpha=2 α=2。
- (a)若將 x x x擴大 10 倍,概率密度 f ( x ) f(x) f(x)如何變化?
- (b)在雙對數坐標下,曲線斜率是多少?
- 已知某網站訪問量服從冪律分布 f ( x ) = C x ? α f(x) = Cx^{-\alpha} f(x)=Cx?α,其中 α = 2 \alpha=2 α=2。
-
圖形識別
- 給出以下兩組數據(圖略),判斷哪組符合正態分布,哪組符合冪律分布,并說明理由。
- 數據A:直方圖呈鐘形,尾部快速衰減。
- 數據B:雙對數坐標下近似直線,右側長尾顯著。
- 給出以下兩組數據(圖略),判斷哪組符合正態分布,哪組符合冪律分布,并說明理由。
提高題(應用與推導)
-
參數估計與假設檢驗
- 使用 Python 對以下數據進行正態分布擬合:
import numpy as np data = np.random.normal(loc=5, scale=2, size=1000)- (a)估計均值和標準差。
- (b)通過 K-S 檢驗判斷是否符合正態分布(顯著性水平 α=0.05)。
- 使用 Python 對以下數據進行正態分布擬合:
-
冪律分布的長尾效應
- 某電商平臺商品銷量數據如下(數據已排序):
sales = [1000, 800, 600, 500, 400, 300, 200, 100, 50, 10]- (a)繪制雙對數坐標圖,判斷是否符合冪律分布。
- (b)估算冪律指數 α \alpha α(提示:對數據進行線性回歸)。
- 某電商平臺商品銷量數據如下(數據已排序):
-
代碼實現與驗證
- 編寫 Python 代碼,生成 1000 個冪律分布樣本( α = 2.5 , x min ? = 1 \alpha=2.5, x_{\min}=1 α=2.5,xmin?=1),并驗證其 CCDF 在雙對數坐標下的直線性。
挑戰題(綜合與創新)
-
混合分布建模
- 現實數據中可能同時包含正態分布和冪律分布成分(如用戶活躍度:中間集中,頭部超活躍)。
- (a)設計一個混合模型:正態分布(占 80%)與冪律分布(占 20%)。
- (b)生成合成數據并可視化其直方圖。
- (c)嘗試用擬合方法分離兩種成分。
- 現實數據中可能同時包含正態分布和冪律分布成分(如用戶活躍度:中間集中,頭部超活躍)。
-
金融風險評估的局限性
- 金融資產收益率常被假設為正態分布,但實際數據存在“肥尾”現象。
- (a)用冪律分布替代正態分布,重新計算 VaR(95% 置信水平)。
- (b)比較兩種方法在極端風險預測上的差異。
- 金融資產收益率常被假設為正態分布,但實際數據存在“肥尾”現象。
-
社交網絡影響力優化
- 某社交平臺用戶粉絲數服從冪律分布( α = 2.0 \alpha=2.0 α=2.0)。
- (a)若要求前 1% 用戶貢獻 50% 的總粉絲量,是否符合當前分布?
- (b)提出一種策略調整 α \alpha α,使得長尾用戶(后 90%)的總粉絲量占比提升至 30%。
- 某社交平臺用戶粉絲數服從冪律分布( α = 2.0 \alpha=2.0 α=2.0)。
答案與提示
基礎題
-
正態分布參數意義
- (a)概率 ≈ 68%( μ ± σ \mu \pm \sigma μ±σ覆蓋范圍)。
- (b)概率增加至約 95%( μ ± 2 σ \mu \pm 2\sigma μ±2σ)。
-
冪律分布的標度不變性
- (a) f ( 10 x ) = C ( 10 x ) ? 2 = C x ? 2 / 100 f(10x) = C(10x)^{-2} = Cx^{-2}/100 f(10x)=C(10x)?2=Cx?2/100,即概率密度降至原來的 1/100。
- (b)斜率為 ? α = ? 2 -\alpha = -2 ?α=?2。
-
圖形識別
- 數據A:正態分布(鐘形曲線)。
- 數據B:冪律分布(雙對數直線 + 長尾)。
提高題
-
參數估計與假設檢驗
- (a)估計均值 ≈ 5,標準差 ≈ 2。
- (b)K-S 檢驗 p 值 > 0.05,接受正態分布假設。
- 代碼參考:
from scipy.stats import norm, kstest mu_est, sigma_est = norm.fit(data) ks_stat, p_value = kstest(data, 'norm', args=(mu_est, sigma_est))
-
冪律分布的長尾效應
- (a)雙對數圖近似直線,符合冪律分布。
- (b)對 log ? f ( x ) = ? α log ? x + 常數 \log f(x) = -\alpha \log x + \text{常數} logf(x)=?αlogx+常數做線性回歸,斜率即 α \alpha α。
-
代碼實現與驗證
- 代碼參考:
from scipy.stats import powerlaw import matplotlib.pyplot as plt data = powerlaw.rvs(2.5, scale=1, size=1000) sorted_data = np.sort(data)[::-1] ccdf = np.arange(1, len(sorted_data)+1)/len(sorted_data) plt.loglog(sorted_data, ccdf, 'b.') plt.show()
- 代碼參考:
挑戰題
-
混合分布建模
- 提示:
- (a)使用
np.random.normal和powerlaw.rvs生成混合數據。 - (b)直方圖呈現中間峰 + 右側長尾。
- (c)嘗試用最大似然法擬合混合參數。
- (a)使用
- 提示:
-
金融風險評估的局限性
- 提示:
- (a)冪律 VaR 計算需積分求分位點: P ( X ≥ x ) = 0.05 P(X \geq x) = 0.05 P(X≥x)=0.05。
- (b)冪律 VaR 遠大于正態分布結果(極端風險更高)。
- 提示:
-
社交網絡影響力優化
- 提示:
- (a)當前頭部 1% 用戶貢獻 ∝ ∫ x 99 % ∞ x ? x ? 2 d x ∝ 1 / x 99 % \propto \int_{x_{99\%}}^\infty x \cdot x^{-2} dx \propto 1/x_{99\%} ∝∫x99%?∞?x?x?2dx∝1/x99%?,需計算具體比例。
- (b)增大 α \alpha α(如 α = 2.5 \alpha=2.5 α=2.5)可減少頭部集中度。
- 提示:
反饋與答疑
- 常見疑問解答:
- Q1:如何判斷數據是正態分布還是冪律分布?
A:正態分布直方圖對稱且尾部快速衰減;冪律分布雙對數坐標下為直線。 - Q2:為何冪律分布的方差可能無限?
A:當 α ≤ 3 \alpha \leq 3 α≤3時,積分 ∫ x 2 f ( x ) d x \int x^2 f(x) dx ∫x2f(x)dx發散,導致方差不存在。 - Q3:如何處理數據中的混合分布?
A:可使用高斯混合模型(GMM)或貝葉斯方法分離成分,或通過分段擬合。
- Q1:如何判斷數據是正態分布還是冪律分布?






:pinctrl 子系統詳解與實戰分析)
)



)
)




)

