1. 簡單題

我的答案:時間復雜度過高:O(N^3)
class Solution:def twoSum(self, nums: List[int], target: int) -> List[int]:for num in nums:if (target - num) in nums:#多余for i in range(len(nums)):if nums[i] == num :for j in range(i+1,len(nums)):if nums[j] == (target - num) :return [i,j]
官方題解:
#暴力枚舉,時間復雜度:O(N^2)
class Solution:def twoSum(self, nums: List[int], target: int) -> List[int]:n = len(nums)for i in range(n):for j in range(i + 1, n):if nums[i] + nums[j] == target:return [i, j]return []作者:力扣官方題解
鏈接:https://leetcode.cn/problems/two-sum/solutions/434597/liang-shu-zhi-he-by-leetcode-solution/
來源:力扣(LeetCode)
著作權歸作者所有。商業轉載請聯系作者獲得授權,非商業轉載請注明出處。#哈希表,時間復雜度:O(N),此時找target - num的時間復雜度變為O(1)
class Solution:def twoSum(self, nums: List[int], target: int) -> List[int]:hashtable = dict()#創建一個空字典哈希數組,用于存儲已經遍歷過的數字和她們的索引for i, num in enumerate(nums):#使用 enumerate 同時遍歷 nums 中的索引 i 和對應的值 num。if target - num in hashtable:return [hashtable[target - num], i]hashtable[nums[i]] = ireturn []作者:力扣官方題解
鏈接:https://leetcode.cn/problems/two-sum/solutions/434597/liang-shu-zhi-he-by-leetcode-solution/
來源:力扣(LeetCode)
著作權歸作者所有。商業轉載請聯系作者獲得授權,非商業轉載請注明出處。
2. 中等題

官方題解
#最小堆,堆的時間復雜度是O(log n),故總的時間復雜度為O(nlog n)
#初始時堆為空,將最小丑數1加入堆,每次取出堆頂元素x,x是堆中最小的丑數,則把2X,3X,5X都加入堆,用哈希集去重
class Solution:def nthUglyNumber(self,n: int) -> int:factors = [2,3,5]seen = {1}heap = [1]for i in range(n-1):curr = heapq.heappop(heap) #返回堆中最小元素for factor in factors:if (num := curr * factor) not in seen:seen.add(num)heapq.heappush(heap,num)#將數存入堆中并保存堆的結構return heapq.heappop(heap)
#優先隊列,利用三個指針的移動,需要計算丑數數組中的n個數,故時間復雜度為O(n)
class Solution:def nthUglyNumber(self,n: int) -> int:dp = [0]*(n+1)p2 = p3 = p5 =1dp[1] = 1 for i in range(2,n+1):num2,num3,num5 = dp[p2]*2,dp[p3]*3,dp[p5]*5dp[i]=min(num2,num3,num5)if dp[i] == num2:p2+=1 if dp[i] == num3:p3+=1if dp[i] == num5:p5+=1return dp[n]
3. 美團筆試錯題

def calculate_alternate_steps():T = int(input()) # 次數for _ in range(T):n = int(input())arr_str = input().strip()arr = [0] + list(map(int, list(arr_str))) # 下標從1開始start = int(input())left_steps = 0right_steps = 0visited = set()current_index = startdirection = 'right' # 初始向右while True:visited.add(current_index)current_value = arr[current_index]next_index = -1if direction == 'right':for i in range(current_index + 1, n + 1):if arr[i] > current_value and i not in visited:next_index = iright_steps += 1breakdirection = 'left' # 切換方向else: # direction == 'left'for i in range(current_index - 1, 0, -1):if arr[i] > current_value and i not in visited:next_index = ileft_steps += 1breakdirection = 'right' # 切換方向if next_index == -1:break # 沒找到更大的,停止current_index = next_indexprint(f"{right_steps} {left_steps}")4. 字母異位分詞

- 方法一:排序
邏輯:互為異位詞的兩個字符串包含的字母相同,因此對兩個字符串分別進行排序后得到的字符串一定相同,可將排序之后的字符串作為哈希表的鍵。
時間復雜度:對于每個字符串,需要O(klogk)的時間排序,以及O(1)的時間更新哈希表,有n個字符串,故時間復雜度為O(nklogk),k為字符串的最大長度。
class Solution:def groupAnagrams(self,strs:List[str]) -> List[List[str]]:mp = collections.defaultdict(list) #創建一個默認順序的哈希表,key是排序后的字符串,value是一個list,存放對應的原始字符串,defaultdict的好處是當key不存在時,自動創造一個空列表,不用手動創建for st in strs:key = "".join(sorted(st))#對字符串進行排序;"".join()表示將()里的重新拼接成一個新的字符串mp[key].append(st)#把字符串加進list中return list(mp.values())
- 方法二:計數
異位的詞中各個字母計數也相同,可以將每個字母出現的次數用字符串表示,作為哈希表的鍵。
時間復雜度: O ( n ( k + ∣ Σ ∣ ) ) O(n(k+|\Sigma|)) O(n(k+∣Σ∣)),n為字符串個數,k為字符串最大長度, ∣ Σ ∣ |\Sigma| ∣Σ∣為字符集長度,此處為26;對于每個字符串,需要對其k個字母進行計數, O ( ∣ Σ ∣ ) O(|\Sigma|) O(∣Σ∣)的時間生成哈希表的鍵,同時以及O(1)的時間寫進哈希表。
##異位的詞中各個字母計數也相同,可以將每個字母出現的次數用字符串表示,作為哈希表的鍵
class Solution:def groupAnagrams(self,strs:List[str]) -> List[List[str]]:mp = collections.defaultdict(list)for st in strs:counts=[0]*26for ch in st:counts[ord(ch) - ord("a")] += 1 #構建了一個列表,將'a'~'z'映射到數組下標0~25,ord(ch)得到字符的ASCII碼# 需要將list轉換為tuple才能進行哈希,因為list是mutable類型(可變類型),可以將如a=[1,2,3];a[0]=100;print(a)顯示a=[100,2,3],此即可變類型;mutable類型不能當哈希表的keymp[tuple(counts)].append(st)return list(mp.values())
5. 最長連續序列

- 利用哈希表,根據數是否是開頭來判斷是否跳過內層循環
利用哈希表對每個數判斷是否是連續序列開頭的數,如果該數的前一個在序列中,說明肯定不是開頭,直接跳過;因此,只要對每個開頭的數進行循環,直到這個序列不再連續
即每個數進行內層進行一次循環,外層為O(n),故時間復雜度為O(n)
class Solution:def longestConsecutive(self, nums: List[int]) -> int:longest_streak = 0num_set = set(nums) #對nums進行去重for num in num_set:if num - 1 not in num_set:current_num = numcurrent_streak = 1while current_num + 1 in num_set:current_num += 1current_streak += 1longest_streak = max(longest_streak,current_streak)return longest_streak
6. 利用雙指針移動零

- 利用雙指針
使用雙指針,左指針指向當前已經處理好的序列尾部,右指針指向待處理序列的頭部;右指針不斷向右移動,每次右指針指向非零數,則將左右指針對應的數交換,同時左指針右移;左右指針中間全為零。
兩個指針同時移動,每個位置最多被遍歷兩次,時間復雜度為O(n)
class Solution:def moveZeroes(self,nums:List[int]) -> None:n = len(nums)left = right = 0 while right < n:if nums[right] != 0:nums[left],nums[right] = nums[right],nums[left]#相當于左指針停滯不前,指向右指針原先指向的0,因此需要交換位置left += 1right += 1
7. 雙指針:容器可以裝的最多的水

- 利用雙指針框出左右邊界
每次以雙指針為左右邊界,移動更小數的那個指針,如果是左指針則右移,右指針則左移。
雙指針總計最多遍歷整個數組一次,時間復雜度為O(n)
class Solution:def maxArea(self,height:List[int]) -> int:l,r = 0,len(height) -1ans = 0while l < r:area = min(height[l], height[r])*(r-l)ans = max(ans,area)if height[l] <= height[r]:l+=1else:r-=1return ans
8. 二叉樹的中序遍歷及其延伸

- 樹的中序遍歷:按照訪問左子樹-根節點-右子樹的方式遍歷這棵樹,在訪問左子樹的時候按照同樣的方式遍歷,直到遍歷完整顆樹。
- 方法一:利用遞歸
時間復雜度:O(n),n為二叉樹節點的個數;
空間復雜度:O(n),遞歸利用了隱形棧
class Solution:def inorderTraversal(self, root):res = []self.inorder(root, res)return resdef inorder(self, root, res):if not root:returnself.inorder(root.left, res)res.append(root.val)self.inorder(root.right, res)
- 方法二:迭代,上述遞歸時隱式維護了一個棧,迭代時需要將這個棧顯式模擬出來
時間復雜度為O(n),n為二叉樹節點個數,每個節點會被訪問一次且只會被訪問一次;
空間復雜度為O(n),棧占用的空間
class Solution:def inorderTraversal(self, root):res = []stack = []while root or stack:# 1. 一直向左走,壓入棧while root:stack.append(root)root = root.left# 2. 彈出棧頂元素,訪問它root = stack.pop()res.append(root.val)# 3. 轉向右子樹root = root.rightreturn res
- 方法三:morris
比上述多做了一步:假設當前遍歷到的節點為x,將x的左子樹中最右邊的節點的右孩子指向x,這樣在左子樹遍歷完成后我們通過這個指向走回了x而不用通過棧;
時間復雜度:O(n),每個節點被遍歷兩次;
省去了棧的空間復雜度,O(1)。
class Solution:def inorderTraversal(self, root):res = []current = rootwhile current:if current.left:#有左子樹# 找到當前節點左子樹中的最右節點(中序前驅)predecessor = current.leftwhile predecessor.right and predecessor.right != current:predecessor = predecessor.right# 第一次訪問:建立線索if not predecessor.right:predecessor.right = currentcurrent = current.leftelse:# 第二次訪問:恢復結構 + 訪問當前節點predecessor.right = None#置空res.append(current.val)current = current.rightelse:# 沒有左子樹,直接訪問當前節點res.append(current.val)current = current.rightreturn res
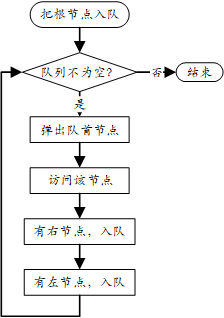
- 二叉樹的層次遍歷:按照從上到下、從左到右的順序一層一層訪問樹的節點。是一種廣度優先搜索方法,通常使用隊列實現。實現邏輯為:
| 題型 | 說明 |
|---|---|
| 🔁 按層反轉 | 每一層從右到左打印(Z字形遍歷) |
| 📐 記錄層數/高度 | 層數 = 階段數,BFS循環幾輪就是幾層 |
| 🌠 找到每層最大值 | 每一層記錄最大值 |
| 🎯 節點的最短路徑 | BFS是天然找最短路徑的利器 |
| 🔗 右視圖/左視圖節點 | 每層最右/最左節點 |
| 📦 序列化和反序列化 | 層序遍歷是常用方式之一 |
- 深度優先搜索:是種“一條路走到底”的搜索方法,他優先沿某一條路走下去,走到底了再返回上一個交叉點走另一條路。
常用數據結構:遞歸(系統棧)或手動棧 - 廣度優先搜索哦:是種“從近到遠”的搜索方法,他一層一層地遍歷節點,先訪問第一層,再訪問第二層。
常用數據結構:隊列 - 無論是深度優先搜索還是廣度優先搜索,其時間復雜度都是遍歷的所有節點和邊的成本O(n+m);但空間復雜度廣度優先搜索會更高一些(排隊的節點更多)。
兩者區別:
| 對比項 | DFS(深度優先) | BFS(廣度優先) |
|---|---|---|
| 搜索方式 | 一條路走到底,再回退 | 一層一層來,逐層擴展 |
| 使用數據結構 | 棧(或遞歸) | 隊列 |
| 空間復雜度 | 最壞O(n)(取決于深度) | 最壞O(n)(取決于寬度) |
| 尋找路徑 | 不一定是最短路徑 | 一定能找最短路徑(無權圖) |
| 應用場景 | 回溯、樹遞歸、組合問題、圖連通 | 層級問題、最短路徑、最小步數 |
| 實現方式 | 遞歸寫法更自然 | 需要手動隊列實現 |
9. 二叉樹的最大深度

- 方法一:深度優先搜索
利用遞歸,先計算左子樹深度和右子樹深度,樹的深度即兩者最大+1;
時間復雜度:O(n),每個節點只被遍歷一次
class Solution:def maxDepth(self,root):if root is None:return 0else:left_height = self.maxDepth(root.left)right_height = self.maxDepth(root.right)return max(left_height,right_height) +1
- 方法二:廣度優先搜索
利用隊列,將[每次從隊列拿出一個節點]改為[每次將隊里了里的所有節點拿出來擴展],這樣能保證每次拓展完的時候隊列里存放的是當前層的所有節點,最后用一個變量來維護拓展的次數,該二叉樹的最大深度即為拓展次數;
時間復雜度:O(n),每個節點只被訪問一次。
class Solution:def maxDepth(self,root):if not root:returnqueue = deque([root])#加入根節點ans = 0while queue:size = len(queue)#當前層的節點數for _ in range(size):#對于該層的所有節點都進行左右節點拓展node = queue.popleft()if node.left:queue.append(node.left)if node.right:queue.append(node.right)ans += 1 #處理完一層后深度+1return ans
- 如何用python實現隊列
| 方法 | 適用場景 | 入隊 | 出隊 | 是否推薦 |
|---|---|---|---|---|
collections.deque | 通用算法題 / BFS | append() | popleft() | ? 推薦 |
queue.Queue | 多線程 / 并發編程 | put() | get() | ? 推薦(多線程) |
list | 簡單腳本 | append() | pop(0) | ? 不推薦(效率低,pop的時間復雜度為O(n)) 因為list底層是動態數組,刪除頭部元素后需要將后續前移,故時間復雜度為O(n) |
舉例:
## collections.deque
from collections import dequequeue = deque()# 入隊
queue.append(10)
queue.append(20)# 出隊
x = queue.popleft() # 返回10# 判空
if not queue:print("隊列為空")## queue.Queue
from queue import Queuequeue = Queue()# 入隊
queue.put(10)# 出隊
x = queue.get()# 判空
if queue.empty():print("隊列為空")## list模擬
queue = []# 入隊
queue.append(10)# 出隊(效率低)
x = queue.pop(0)
10. 翻轉二叉樹

- 利用遞歸;交換左右子樹的位置即可
時間復雜度:O(n),n為樹的節點,會遍歷樹的每個節點,對于每個節點,在常數時間內交換兩個子樹
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def invertTree(self,root: TreeNode) -> TreeNode:if not root:return rootleft = self.invertTree(root.left)right = self.invertTree(root.right)root.left,root.right = root.right,root.leftreturn root
11. 對稱二叉樹

- 方法一:遞歸
同步移動兩個指針,兩指針先同時指向根節點,接著,一個指針左移,一個指針右移,每次檢查當前指針的值是否相等,如果相等再判斷左右子樹是否對稱;
時間復雜度:O(n),對于每個節點都會遍歷
class Solution:def isSymmetric(self, root: Optional[TreeNode]) -> bool:# 內部輔助函數:遞歸比較左右子樹是否鏡像對稱def check(p, q):if not p and not q:return True # 兩個都是空,說明對稱if not p or not q:return False # 一個空一個非空,不對稱return (p.val == q.val andcheck(p.left, q.right) andcheck(p.right, q.left))return check(root.left, root.right)
12.二叉樹的直徑

- 深度優先搜索
路徑可以看成經過的節點數減一;且可以看成由某個節點為起點,其左兒子和右兒子的和(節點數為左兒子加右兒子+1,路徑需要再減1);遍歷所有節點得到左兒子和右兒子的和,取最大即可得到二叉樹的最長路徑;
時間復雜度:O(n),n為二叉樹節點數,遍歷所有節點;
空間復雜度:O(height),height為樹的高度,遞歸需要為每一層遞歸函數分配棧空間,分配空間大小取決于遞歸深度,即樹的高度。
class Solution:def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:self.ans = 0def depth(node):#訪問到空節點,返回0if not node:return 0#左兒子為根的子樹的深度L = depth(node.left)#右兒子為根的子樹的深度R = depth(node.right)#計算d_node即L+R+1,并更新ansself.ans = max(self.ans,L+R)#返回該節點為根的子樹深度return max(L,R)+1depth(root)return self.ans
13. 將有序數組轉換為二叉搜索樹

- 三個方法均是中序遍歷,方法一總是選擇中間位置左邊的數字作為根節點,方法二選擇右邊,方法三在上述兩者中隨機選擇。
時間復雜度:O(n),n為數組長度,每個是數字只訪問一次;
空間復雜度:O(log(n)),構建棧的深度為log(n)。
class Solution:def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:def helper(left,right):if left > right:return None#方法一,總是選擇中間位置左邊的數作為根節點mid = (left+right) // 2#整數除法,向下取整#方法二,總是選擇中間的右邊作為根節點# mid = (left+right+1) // 2#方法三,隨機選擇中間節點的左邊或者右邊作為根節點mid = (left+right+randint(0,1)) // 2root = TreeNode(nums[mid])#確定根節點root.left = helper(left,mid - 1) #遞歸構建左子樹root.right = helper(mid+1,right) #遞歸構建右子樹return root return helper(0,len(nums) - 1)
- 二叉搜索樹:是一種特殊的二叉樹,需要滿足:
對于每個節點root:
a. 所有左子樹 < root.val
b. 所有右子樹 > root.val
c. 所有子樹均是二叉搜索樹
常見操作:最壞時間復雜度是因為可能因為不斷插入遞增或遞減序列使二叉樹弱化為鏈表
| 操作 | 描述 | 平均時間復雜度 | 最壞時間復雜度 |
|---|---|---|---|
| 插入(Insert) | 插入一個新值 | O(log n) | O(n) |
| 查找(Search) | 查找一個值是否存在 | O(log n) | O(n) |
| 刪除(Delete) | 刪除一個值(需要分情況處理) | O(log n) | O(n) |
| 最小值/最大值 | 找最小值:最左節點;最大值:最右節點 | O(log n) | O(n) |
遍歷方式:
| 遍歷方式 | 順序 | 應用場景 |
|---|---|---|
| 中序遍歷 | 左 → 根 → 右 | 升序輸出 BST 中所有值 |
| 前序遍歷 | 根 → 左 → 右 | 用于復制樹結構 |
| 后序遍歷 | 左 → 右 → 根 | 用于刪除樹結構 |
| 層序遍歷 | 一層一層從上往下 | 常用于廣度優先搜索(BFS) |
刪除操作(三種情況):
a. 葉子節點:直接刪除
b. 只有一個子節點:用子節點替代它
c. 該節點有兩個子節點:找右子樹的最小值(或左子樹最大值);用其替換當前節點,再遞歸刪除該值
class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightclass Solution:def deleteNode(self, root, key):if not root:return None#找到值對應的節點,小于往左,大于往右if key < root.val:root.left = self.deleteNode(root.left, key)elif key > root.val:root.right = self.deleteNode(root.right, key)else:# 找到目標節點,開始刪除#單個節點,直接替換if not root.left:return root.rightif not root.right:return root.left# 兩個子節點:找右子樹最小值min_larger_node = self.getMin(root.right)root.val = min_larger_node.valroot.right = self.deleteNode(root.right, min_larger_node.val)#再在右子樹中刪除這個最小值return rootdef getMin(self, node):while node.left:node = node.left#由于是對右子樹找最小,右子樹的最左節點就是最小值return node
時間復雜度:查找要刪除的節點/找右子樹的最小值/遞歸刪除該最小節點;三個步驟都是最多耗時O(h),h為樹的高度;當樹為平衡二叉樹時, h = l o g ( n ) h=log(n) h=log(n),退化為鏈表時 h = n h=n h=n。
| 情況 | 時間復雜度 |
|---|---|
| 平衡二叉搜索樹(理想情況) | O(log n) |
| 退化為鏈表(最壞情況) | O(n) |
相關擴展結構:
| 數據結構 | 特點 |
|---|---|
| AVL樹 | 平衡二叉搜索樹,插入/刪除時自動保持左右子樹高度差不超過1 |
| 紅黑樹 | 一種自平衡二叉搜索樹,插入和刪除更高效,廣泛用于 STL、Java |
| Treap / Splay Tree | 更復雜的平衡機制,適合頻繁操作或對時間復雜度有更高要求 |
| Segment Tree | 區間操作優化,但不是嚴格意義上的 BST |
平衡二叉樹:對于任意節點,其左子樹和右子樹的高度差小于等于1,所有子樹也是平衡二叉樹。
為什么需要平衡?發現右子樹過高時會自動左旋,避免樹退化為鏈表。
常見的平衡二叉樹:
| 類型 | 特點 |
|---|---|
| AVL樹 | 每個節點維護平衡因子,嚴格控制高度差不超過 1,查找快但插入稍慢(最典型的二叉樹) |
| 紅黑樹 | 通過顏色控制近似平衡,高度最多為 2log n,Java、C++ STL 使用 |
| Splay樹 | 每次訪問后將該節點“旋轉”到根,適合頻繁訪問某些節點的場景 |
| Treap | 結合 BST + 堆的性質,使用隨機優先級構建 |
操作時間復雜度:
| 操作 | 時間復雜度 |
|---|---|
| 查找 | O(log n) |
| 插入 | O(log n) |
| 刪除 | O(log n) |
14. 樹的層序遍歷

- 方法一:利用廣度優先遍歷每個節點,每層均判斷層中節點數。
時間復雜度:O(n),每個節點均被訪問一次;
空間復雜度:O(n),隊列+輸出。
class Solution:def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:res = []if not root:return res queue = deque([root])while queue:size = len(queue)#當前層隊列中節點數level = []for _ in range(size):node = queue.popleft()level.append(node.val)if node.left:queue.append(node.left)if node.right:queue.append(node.right)res.append(level)return res
- 方法二:利用哈希表
時間復雜度:O(n+hlog(h)),每個節點訪問一次,最后需要對哈希表鍵值排序輸出,時間復雜度為hlog(h),h為樹的高度
空間復雜度:O(n),隊列+哈希表+輸出
class Solution:def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:if not root:return []level_map = defaultdict(list) # 哈希表:level -> list of node valuesqueue = deque()queue.append((root, 0)) # 初始狀態為根節點和其層級 0while queue:node, level = queue.popleft()level_map[level].append(node.val)#通過二元組加入哈希表if node.left:queue.append((node.left, level + 1))if node.right:queue.append((node.right, level + 1))# 將 level_map 按 level 從小到大取值組成結果return [level_map[i] for i in sorted(level_map.keys())]
15. 判斷樹是否是二叉搜索樹

- 方法一:利用遞歸,判斷該節點是否在上下界里,其左右子樹是否是二叉搜索樹即可。
時間復雜度:O(n),每個節點均被訪問一次;
空間復雜度:O(n),構建棧的深度為樹的高度,最壞情況為n。
class Solution:def isValidBST(self, root: Optional[TreeNode]) -> bool:def helper(node,lower = float('-inf'),upper=float('inf')) -> bool:if not node:return Trueval = node.val#判斷節點值是否滿足if val <= lower or val >= upper:return False #遞歸判斷左右子樹是否是二叉搜索樹if not helper(node.right,val,upper):return Falseif not helper(node.left,lower,val):return Falsereturn Truereturn helper(root)
- 方法二:中序遍歷時實時檢查當前節點值是否大于前一個中序遍歷得到的節點值,一旦發生不大于,則該樹并非二叉搜索樹;利用棧實現中序遍歷。
時間復雜度:O(n),每個節點最多被訪問一次;
空間復雜度:O(n),棧最多存儲n個節點,因此額外需要O(n)的空間。
class Solution:def isValidBST(self,root:TreeNode) -> bool:stack,inorder = [],float('-inf')while stack or root:#把左子樹節點全部壓入棧中while root:stack.append(root)root = root.leftroot = stack.pop()#如果中序遍歷得到的節點的值小于前一個inorder,說明不是二叉搜索樹if root.val <= inorder:return Falseinorder = root.valroot = root.rightreturn True
16. 找到二叉搜索樹中第k小的元素

- 方法一:利用中序遍歷,邊遍歷邊計數,計到第k個即第k小的數。
時間復雜度:O(h+k),h是樹的高度,開始遍歷前,需要到達最左的葉子節點;
空間復雜度:O(h),棧中最多需要存儲h個元素。
class Solution:def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:stack=[]#res = [],可以省去該記錄,直接用k計數即可while stack or root:while root:stack.append(root)root = root.leftroot = stack.pop()# res.append(root.val)# if len(res) == k:# return res[k-1]k-=1if k == 0:return root.valroot = root.right
- 方法二:用于優化需要頻繁查找第k小的值;利用樹重建,同時記錄子樹的節點數;對每個節點判斷其左子樹節點數和k的大小。
時間復雜度:O(n),需要遍歷樹中所有的節點來統計節點數,搜索的時間復雜度為O(H),H為樹的高度;
空間復雜度:O(n),用于存儲以每個節點為根節點的子樹節點數。
class MyBst:def __init__(self,root: TreeNode):self.root = root#統計以每個節點為根節點的子樹的節點樹,并記錄在哈希表中self._node_num = {}#用于存儲每個節點的子樹節點數self._count_node_num(root)def kth_smallest(self,k: int) -> int:#返回樹中第k小的元素node = self.rootwhile node:left = self._get_node_num(node.left)#得到左子樹的節點數if left < k - 1:#左子樹總節點數小于knode = node.right#節點右移k -= left+ 1elif left == k - 1:return node.valelse:node = node.left#第k小的節點在左子樹中def _count_node_num(self,node) -> int:#統計以node為節點的子樹節點數if not node:return 0self._node_num[node] = 1 + self._count_node_num(node.left) + self._count_node_num(node.right)return self._node_num[node]def _get_node_num(self,node) -> int:#獲取以node為根節點的子樹節點數return self._node_num[node] if node is not None else 0class Solution:def kthSmallest(self,root: TreeNode,k: int) -> int:bst = MyBst(root)return bst.kth_smallest(k)
- 方法三:如果二叉樹經常被修改(插入/刪除操作)并且你需要頻繁地查找第k小的值,可以將二叉搜索樹變平衡。構建好平衡二叉搜索樹后修改成本降低。
時間復雜度:O(n),構建樹全部節點的時間,增、刪、搜索的時間復雜度均為O(log(n));
空間復雜度:O(n),用于存儲平衡二叉樹。
class AVL:#定義一個平衡二叉樹,允許重復值#定義平衡二叉樹的節點class Node:__slots__ = ("val","parent","left","right","height","size")def __init__(self,val,parent = None,left=None,right = None):self.val = valself.parent = parentself.left = leftself.right = rightself.height = 0#默認葉子節點高度為0self.size = 1#當前節點為根節點時子樹節點數#構建二叉樹def __init__(self,vals):self.root = self._build(vals,0,len(vals) - 1,None) if vals else Nonedef _build(self,vals,l,r,parent):#根據vals[l:r]構建平衡二叉樹,并返回根節點m = (l+r) // 2node = self.Node(vals[m],parent=parent)if l <= m -1:#遞歸構建左子樹node.left = self._build(vals,l,m - 1,parent=node)if m+1 <= r:node.right = self._build(vals,m+1,r,parent=node)self._recompute(node)#重新計算每個子樹的高度和元素數return nodedef _recompute(self,node):#重新計算每個子樹的高度和元素數node.height = 1+ max(self._get_height(node.left),self._get_height(node.right))node.size = 1+ self._get_size(node.left) + self._get_size(node.right)def _get_height(self,node) -> int:return node.height if node is not None else 0def _get_size(sellf,node) -> int:return node.size if node is not None else 0def kth_smallest(self,k: int):node = self.rootwhile node:left = self._get_size(node.left)if left < k -1:node = node.rightk -= left+1elif left == k - 1:return node.valelse:node = node.left #對二叉樹進行增刪改除操作#插入值為v的節點def insert(self,v):if self.root is None:self.root = self.Node(v)else:#計算新節點的位置#在子樹中找到值為v的位置node = self._subtree_search(self.root,v)is_add_left = (v<= node.val)#判斷是否加在節點左邊if node.val == v:if node.left:#如果值為v的節點存在且其有左子節點,則將其加在左子樹的最右邊node = self._subtree_last(node.left)is_add_left = Falseelse:is_add_left = True#添加新節點leaf = self.Node(v,parent=node)if is_add_left:node.left = leafelse:node.right = leafself._rebalance(leaf)#使樹重新平衡def _rebalance(self,node):#從node節點開始逐個向上重新平衡二叉樹,并更新高度和元素數while node is not None:old_height,old_size=node.height,node.size if not self._is_balanced(node):#判斷此時是否平衡node = self._restructure(self._tall_grandchild(node))self._recompute(node.left)self._recompute(node.right)self._recompute(node)if node.height == old_height and node.size == old_size:#如果節點高度和元素數都沒有變化則不需要再繼續向上調整node = None else:node = node.parent def _is_balanced(self,node):#判斷是否平衡return abs(self._get_height(node.left) - self._get_height(node.right)) <= 1def _tall_child(self,node):#獲取node節點更高的子樹if self._get_height(node.left) > self._get_height(node.right):return node.leftelse:return node.rightdef _tall_grandchild(self,node):#獲取節點更高的子樹里節點更高的子樹child = self._tall_child(node)return self._tall_child(child)def _restructure(self,node):#重建parent = node.parentgrandparent = parent.parent if (node == parent.right) == (parent == grandparent.right):#處理一次需要旋轉的情況self._rotate(parent)return parentelse:#處理需要兩次旋轉的情況self._rotate(node)self._rotate(node)return node def _rotate(self,node):#旋轉parent = node.parentgrandparent = parent.parentif grandparent is None:self.root = node node.parent = Noneelse:self._relink(grandparent, node, parent == grandparent.left)#如果父節點在祖父節點的左邊,則將node連接到祖父的左邊,否則,連接到祖父的右邊if node == parent.left:self._relink(parent,node.right,True)#如果節點在父節點的左邊,則將節點的右子節點連接到父節點左邊self._relink(node,parent,False)#將父節點連接到節點右邊else:self._relink(parent,node.left,False)#節點在父節點右邊,則將節點的左子節點連接到父節點右邊self._relink(node,parent,True)#將父節點連接到節點的左邊#is_left為真則將child連接到parent的左邊,否則,連到parent的右邊@staticmethoddef _relink(parent,child,is_left):#重新鏈接父節點和子節點,子節點允許為空if is_left:parent.left = childelse:parent.right = childif child is not None:child.parent = parent#刪除操作def delete(self,v) -> bool:if self.root is None:return False node = self._subtree_search(self.root,v)#找到值為v的節點if node.val != v:#沒有找到需要刪除的節點return False #處理當前節點既有左子樹也有右子樹的情況#若左子樹比右子樹高度低,則將當前節點替換為右子樹最左側的節點,并移除右子樹最左側的節點#若右子樹比左子樹高度低,則將當前節點替換為左子樹最右側的節點,并移除左子樹最右側的節點if node.left and node.right:if node.left.height <= node.right.height:replacement= self._subtree_first(node.right)#找到右子樹最左else:replacement = self._subtree_last(node.left)#找到左子樹最右node.val = replacement.valnode = replacementparent = node.parentself._delete(node)self._rebalance(parent)return Truedef _delete(self,node):#刪除節點并用它的子節點代替他,該節點最多只能有一個子節點if node.left and node.right:raise ValueError('node has two children')child = node.left if node.left else node.rightif child is not None:child.parent = node.parent if node is self.root:self.root = childelse:parent = node.parentif node is parent.left:parent.left = childelse:parent.right = child node.parent = node def _subtree_first(self,node):#返回以node為根節點的子樹的第一個元素while node.left is not None:node = node.left return node def _subtree_last(self,node):#返回以node為根節點的子樹的最后一個元素while node.right is not None:node = node.rightreturn nodedef _subtree_search(self,node,v):#在以node為根節點的子樹中搜索值為v的節點,如果沒有,則返回值為v的節點應該在的位置的父節點if node.val < v and node.right is not None:return self._subtree_search(node.right,v)if node.val > v and node.left is not None:return self._subtree_search(node.left,v)else:return nodeclass Solution:def kthSmallest(self,root: TreeNode,k: int) -> int:def inorder(node):if node.left:inorder(node.left)inorder_lst.append(node.val)if node.right:inorder(node.right)#中序遍歷生成數值列表inorder_lst = []inorder(root)#構造平衡二叉搜索樹avl = AVL(inorder_lst)#模擬1000次插入和刪除操作random_nums = [random.randint(0,10001) for _ in range(1000)]for num in random_nums:avl.insert(num)random.shuffle(random_nums) #列表亂序for num in random_nums:avl.delete(num)return avl.kth_smallest(k)
17. 二叉樹展開為鏈表

- 方法一:二叉樹展開為鏈表之后會破壞二叉樹的結構,因此在前序遍歷(深度優先搜索:遞歸/迭代)結束之后更新各個節點的左右子節點的信息。
時間復雜度:O(n),其中,n為二叉樹的節點數,前序遍歷的時間復雜度為O(n),更新各個節點信息也是O(n);
空間復雜度:O(n),棧內元素不會超過n個
class Solution:def flatten(self,root: TreeNode) -> None:preorderList = list()def preorderTraversal(root:TreeNode):if root:preorderList.append(root)preorderTraversal(root.left)preorderTraversal(root.right)preorderTraversal(root)size = len(preorderList)for i in range(1,size):prev,curr = preorderList[i-1],preorderList[i]prev.left = Noneprev.right = curr#通過迭代實現前序遍歷
class Solution:def flatten(self,root: TreeNode) -> None:preorderList = list()stack = list()node = rootwhile node or stack:while node:preorderList.append(node)stack.append(node)#先把左子節點全部放進來node = node.leftnode = stack.pop()#從低部開始node = node.right#重拾右子節點,并排查右子節點的左子樹 size = len(preorderList)for i in range(1,size):prev,curr = preorderList[i-1],preorderList[i]prev.left = Noneprev.right = curr
- 方法二: 前序遍歷和展開同步進行,在遍歷左子樹之前獲得左右子節點的信息并存入棧中;對迭代遍歷進行修改,每次從棧內彈出一個節點作為當前訪問的節點,獲得該節點的子節點,如果子節點不為空,則依次將右子節點和左子節點壓入棧內。
時間復雜度:O(n),每個節點均被訪問一次;
空間復雜度:O(n),棧的空間。
class Solution:def flatten(self,root: Optional[TreeNode]) -> None:if not root:returnstack = [root]prev = Nonewhile stack:curr = stack.pop()if prev:prev.left = Noneprev.right = currleft,right = curr.left,curr.rightif right:stack.append(right)if left:stack.append(left)prev = curr
- 方法三:尋找前驅節點,將空間復雜度降為O(1);即對于當前節點,如果左子節點不為空,則將其右子節點賦給左子節點的最右子節點作右子節點;然后將當前節點的左子節點賦給當前節點的右子節點。
時間復雜度:O(n),每個節點均被訪問一次;
空間復雜度:O(1),不需要棧,直接在樹中改。
class Solution:def flatten(self,root: TreeNode) -> None:curr = rootwhile curr:if curr.left:predecessor = nxt = curr.leftwhile predecessor.right:precedessor = predecessor.rightprecedessor.right = curr.rightcurr.left = Nonecurr.right = nxtcurr = curr.right

)



-加載、控制)
:淺析ATAM 在軟件技術架構評估中的應用)






)



:從入門到精通)

