輾轉相除法是用于求取最大公約數時需要用到的方法，它還有個名字稱為繩子算法，這類題目只要理解輾轉相處的原理即可拿下。

一、輾轉相除法的基本原理

兩個整數的最大公約數不變，當較大數減去較小數后，得到的差值與較小數的最大公約數相同。以下是算法的步驟：

1.設兩個正整數 a 和 b ，且 a > b 。

2.用 a 除以 b ，得到余數 r (0 < r < b) 。

3.如果 r 為 0 ，則 b 即為兩數的最大公約數。

4.如果 r ≠ 0 ，則令 a = b ， b = r ，并返回第二步。

這個過程將不斷重復，每次都會產生一個更小的正整數，直到余數為 0 ，此時的 b 就是最大公約數。

二、往年題目

1.（CIE-202203）求最大公約數

1.準備工作

（1）保留默認白色背景和小貓角色。

2.功能實現

（1）輸入兩個正整數；

（2）小貓說出這兩個數的最大公約數。

解題思路：

第①步：通過詢問得到兩個整數，運用詢問和，第二次的回答將頂替掉第一次的回答，那么可以通過變量的設置，然后讓回答存儲到相對應的變量中。

第②步：判斷a是否大于b，如果不滿足，那么變量進行交換，在交換的過程中，需要一個中介的變量，要不然待會無法完成交換的操作（詳細的原因可以看第13課的變量互換）

第③步：用 a 除以 b ，得到余數c (0 <c < b),將得到的余數進行判斷，是否等于0，等于0，跳出循環，這時可以運用（這個命令是重復執行直到滿足條件就跳出循環，不滿足條件就繼續循環的操作），那么條件就是

第④步：?若余數c不等于0，那么令 a = b ， b =c，并繼續相除?

第⑤步：余數等于0停止循環，輸出最大公約數。

整合代碼：

2.（CIE-202104）繩子算法

故事情境：最近在學繩子算術的小星星非常苦惱，他常常在想，如果有一款程序能實現根據輸入的兩根繩子長度，可以把兩根長繩截成長度相等的小段后，直接求出一共可以截成多少段，每段最長多少米就好了。小貓知道后，決定設計一個程序幫助小星星走出繩子算術的困境。

1.準備工作

(1)保留舞臺默認白色背景及小貓角色，將小貓角色調整到舞臺上合適的位置；

(2)建立名為“繩子”的列表用于存儲數據。

2.功能實現

(1)點擊綠旗，詢問“輸入繩子長度”并等待；

(2)將輸入的繩子長度保存到列表“繩子”后，小貓分別說兩根繩子的長度3秒；

(3)根據輸入的兩根繩子長度，設計算法實現：把兩根長繩截成長度相等的小段。求出一共可以截成多少段，每段最長多少米；

(4)計算完成后，小貓分別說“一共可以截成多少段，每段最長多少米。”3秒。

解題思路：

第①步：詢問“輸入繩子長度”并等待，將得到的回答插入到列表中

第②步：將兩條繩子的長度說出來，那么這時候，可以讓其變量等于第一項和第二項，然后運用字符串拼接的方法，說出兩根繩子的長度

第③步：用 繩子1除以繩子2，得到余數t (0 <t < b),將得到的余數進行判斷，是否等于0，等于0，跳出循環，這時可以運用（這個命令是重復執行直到滿足條件就跳出循環，不滿足條件就繼續循環的操作），那么條件就是

第④步：?若余數t不等于0，那么令繩子1=繩子2， 繩子2=t，并繼續相除?

第⑤步：余數等于0停止循環，輸出最大公約數???????。

第⑥步：接著，計算段數，最后運用拼接字符串的方法說出每段最長和段數。

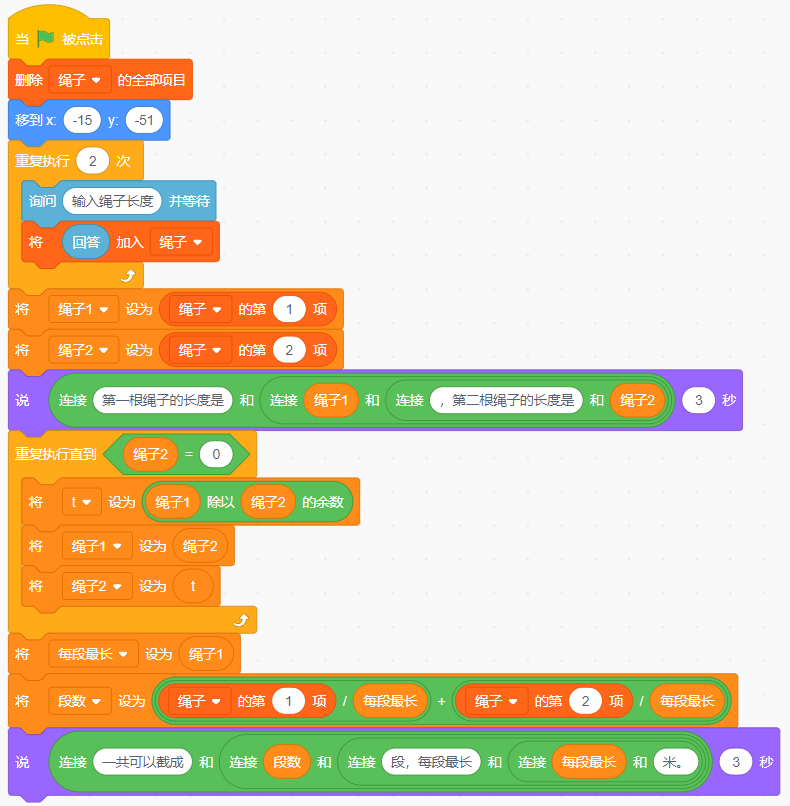
整合代碼：