機器學習決策樹

一、何為決策樹

決策樹（Decision Tree）是一種分類和回歸方法，是基于各種情況發生的所需條件構成決策樹，以實現期望最大化的一種圖解法。由于這種決策分支畫成圖形很像一棵樹的枝干，故稱決策樹。它的運行機制非常通俗易懂，因此被譽為機器學習中，最“友好”的算法。下面通過一個簡單的例子來闡述它的執行流程。假設根據大量數據（含 3 個指標：天氣、溫度、風速）構建了一棵“可預測學校會不會舉辦運動會”的決策樹（如下圖所示）。

1、決策樹的組成

決策樹由結點和有向邊組成。結點有兩種類型：內部結點（圓）和葉結點（矩形）。其中，內部結點表示一個特征（屬性）；葉結點表示一個類別。而有向邊則對應其所屬內部結點的可選項（屬性的取值范圍），有非常好的可解釋性。

2、決策樹的構建

構建要求：

具有較好的泛化能力；
在 1 的基礎上盡量不出現過擬合現象。

思路：

如果按照某個特征對數據進行劃分時，它能最大程度地將原本混亂的結果盡可能劃分為幾個有序的大類，則就應該先以這個特征為決策樹中的根結點。接著，不斷重復這一過程，直到整棵決策樹被構建完成為止。

二、熵

1、熵的作用

熵（Entropy)是表示隨機變量不確定性的度量。說簡單點就是物體內部的混亂程度。我們希望分類后的結果能使得整個樣本集在各自的類別中盡可能有序，即希望某個特征在被用于分類后，能最大程度地降低樣本數據的熵。

根據以上結果，可以很直觀地認為，決策樹 2 的分類效果優于決策樹 1 。決策樹 1 在通過特征 𝑥1 進行分類后，得到的分類結果依然混亂（甚至有熵增的情況），因此這個特征在現階段被認為是無效特征。

2、熵的定義

設 𝑋 是取值在有限范圍內的一個離散隨機變量，其概率密度為：

$P(X=xi)=pi,pi=1,2,......,n$

隨機變量 𝑋 的熵定義為:

當某個集合含有多個類別時，此時 𝑘 較大， 𝑝𝑖?的數量過多；且整體的 𝑝𝑖?都會因 𝑘 的過大而普遍較小，從而使得 𝐻(X) 的值過大。這正好符合“熵值越大，事物越混亂”的定義。

3、條件熵

對于每個特征，都可以算出“該特征各項取值對運動會舉辦與否”的影響（而衡量各特征誰最合適的準則，即是熵）。

定義條件熵 𝐻(𝑌 | 𝑋) ：在給定 𝑋 的條件下 𝑌 的條件概率分布對 𝑋 的數學期望，即

pi?=P(X=xi?)?,?i=1,2,…,k?(表示指定集合中的元素類別) 。

三、劃分選擇

決策樹學習的關鍵在于：如何選擇最優劃分屬性。一般而言，隨著劃分過程的不斷進行，我們自然希望決策樹各分支結點所包含的樣本盡可能屬于同一類別，即結點的 “純度” (purity) 越來越高。下面介紹幾類較為主流的評選算法。

1、信息增益（ ID3 算法選用的評估標準）

信息增益 𝑔(𝐷, 𝑋) ：表示某特征 𝑋 使得數據集 𝐷 的不確定性減少程度，定義為集合 𝐷 的熵與在給定特征 𝑋 的條件下 𝐷 的條件熵 𝐻(𝐷 | 𝑋) 之差，即

信息增益表達了樣本數據在被分類后的專一性。因此，它可以作為選擇當前最優特征的一個指標，依據該指標從大到小依次作為選擇的特征。

2、信息增益率（ C4.5 算法選用的評估標準）

?以信息增益作為劃分數據集的特征時，其偏向于選擇取值較多的特征（特征下的類別很多）。比如，當在學校舉辦運動會的歷史數據中加入一個新特征 “編號” 時，該特征將成為最優特征。因為給定 “編號” 就一定知道那天是否舉行過運動會，因此 “編號” 的信息增益很高。

但實際我們知道，“編號” 對于類別的劃分并沒有實際意義。故此，引入信息增益率。

信息增益率 𝑔𝑅(𝐷, 𝑋) 定義為其信息增益 𝑔(𝐷, 𝑋) 與數據集 𝐷 在特征 𝑋 上值的熵 𝐻𝑋(𝐷) 之比，即：

𝑘 是特征 𝑋 的取值類別個數。

信息增益率能明顯降低取值較多的特征偏好現象，從而更合理地評估各特征在劃分數據集時取得的效果。

3、基尼系數（ CART 算法選用的評估標準）

它通過使用基尼系數來代替信息增益率，從而避免復雜的對數運算。基尼系數代表了模型的不純度，基尼系數越小，則不純度越低，特征越好。注：這一點和信息增益（率）恰好相反。

對于給定數據集 𝐷 ，假設有 𝑘 個類別，且第 𝑘 個類別的數量為 𝐶𝑘?，則該數據集的基尼系數為

如果數據集 D DD 根據特征 X XX 的取值將其劃分為 { D 1 , D 2 , … , D m }，則在特征D的條件下劃分過后的基尼系數為：

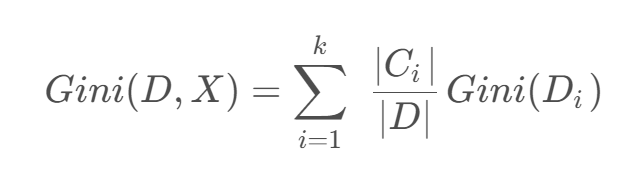
四、實戰

data_loader.py

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_splitdef load_data():"""加載并預處理數據"""data = {'ID': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16],'年齡段': ['青年', '青年', '青年', '青年', '青年', '中年', '中年', '中年', '中年', '中年', '老年', '老年','老年', '老年', '老年', '老年'],'有工作': ['否', '否', '是', '是', '否', '否', '否', '是', '否', '否', '否', '否', '是', '是', '否', '否'],'有自己的房子': ['否', '否', '否', '是', '否', '否', '否', '是', '是', '是', '是', '是', '否', '否', '否','否'],'信貸情況': ['一般', '好', '好', '一般', '一般', '一般', '好', '好', '非常好', '非常好', '非常好', '好', '好','非常好', '一般', '非常好'],'類別(是否給貸款)': ['否', '否', '是', '是', '否', '否', '否', '是', '是', '是', '是', '是', '是', '是', '否','否']}df = pd.DataFrame(data)X = df.drop(['ID', '類別(是否給貸款)'], axis=1)y = df['類別(是否給貸款)']# 劃分訓練集和測試集X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)return X_train, X_test, y_train, y_test, X.columns.tolist()

將原始貸款審批數據轉換為結構化格式，劃分訓練集和測試集，為后續決策樹建模提供可直接使用的輸入。

具體分三步：

1) 用字典定義原始數據并轉為Pandas DataFrame；

2) 分離特征（年齡段、工作、房產、信貸）和標簽（是否貸款）；

3) 按7:3比例隨機拆分訓練集和測試集（固定隨機種子確保可復現），最終返回處理好的特征矩陣、標簽向量及特征名稱列表。

?c45_tree.py

import numpy as np
from collections import Counterclass C45DecisionTree:def __init__(self, max_depth=None, min_samples_split=2):self.max_depth = max_depthself.min_samples_split = min_samples_splitself.tree = Noneself.label_encoders = Nonedef _entropy(self, y):"""計算熵"""counts = np.bincount(y)probabilities = counts / len(y)return -np.sum([p * np.log2(p) for p in probabilities if p > 0])def _information_gain(self, X, y, feature):"""計算信息增益"""total_entropy = self._entropy(y)values, counts = np.unique(X[feature], return_counts=True)weighted_entropy = 0for v, c in zip(values, counts):subset_y = y[X[feature] == v]weighted_entropy += (c / len(y)) * self._entropy(subset_y)return total_entropy - weighted_entropydef _split_info(self, X, feature):"""計算分裂信息"""_, counts = np.unique(X[feature], return_counts=True)probabilities = counts / len(X)return -np.sum([p * np.log2(p) for p in probabilities if p > 0])def _gain_ratio(self, X, y, feature):"""計算信息增益率"""gain = self._information_gain(X, y, feature)split = self._split_info(X, feature)return gain / split if split != 0 else 0def _choose_best_feature(self, X, y, features):"""選擇最佳分裂特征"""gain_ratios = [self._gain_ratio(X, y, f) for f in features]best_idx = np.argmax(gain_ratios)return features[best_idx]def _build_tree(self, X, y, features, depth=0):"""遞歸構建決策樹"""# 終止條件if (len(np.unique(y)) == 1 or(self.max_depth is not None and depth >= self.max_depth) orlen(y) < self.min_samples_split):return {'class': Counter(y).most_common(1)[0][0]}# 選擇最佳特征best_feature = self._choose_best_feature(X, y, features)tree = {'feature': best_feature, 'children': {}}# 遞歸構建子樹remaining_features = [f for f in features if f != best_feature]for value in np.unique(X[best_feature]):subset_X = X[X[best_feature] == value].drop(columns=[best_feature])subset_y = y[X[best_feature] == value]tree['children'][value] = self._build_tree(subset_X, subset_y, remaining_features, depth + 1)return treedef fit(self, X, y):"""訓練模型"""# 將分類特征轉換為數值（簡化實現）self.label_encoders = {}X_encoded = X.copy()for col in X.columns:le = {val: idx for idx, val in enumerate(X[col].unique())}X_encoded[col] = X[col].map(le)self.label_encoders[col] = ley_encoded = y.map({'否': 0, '是': 1})self.tree = self._build_tree(X_encoded, y_encoded, X.columns.tolist())def predict(self, X):"""預測"""X_encoded = X.copy()for col in X.columns:X_encoded[col] = X[col].map(self.label_encoders[col])predictions = []for _, row in X_encoded.iterrows():node = self.treewhile 'children' in node:feature = node['feature']value = row[feature]if value in node['children']:node = node['children'][value]else:breakpredictions.append(node.get('class', 0))return ['是' if p == 1 else '否' for p in predictions]

通過遞歸地選擇信息增益率最大的特征進行節點分裂，構建樹形決策結構。

主要流程分為四步：

1) 預處理階段將分類特征編碼為數值；

2) 基于信息熵計算各特征的信息增益率，選擇最佳分裂特征；

3) 遞歸構建決策樹，直到滿足終止條件（純度100%、達到最大深度或樣本不足）；

4) 預測時根據特征值沿樹結構向下遍歷至葉節點獲取分類結果。該實現完整包含了C4.5算法的關鍵特性：使用增益率避免特征取值數目帶來的偏差，支持預剪枝控制過擬合，并通過字典嵌套結構清晰表示樹的分支關系。

cart_tree.py

import numpy as np
from collections import Counterclass CARTDecisionTree:def __init__(self, max_depth=None, min_samples_split=2):self.max_depth = max_depthself.min_samples_split = min_samples_splitself.tree = Noneself.label_encoders = Nonedef _gini(self, y):"""計算基尼系數"""counts = np.bincount(y)probabilities = counts / len(y)return 1 - np.sum([p ** 2 for p in probabilities if p > 0])def _gini_index(self, X, y, feature):"""計算基尼指數,基于指定特征 X XX 進行劃分后，集合 𝐷 的不確定性"""values, counts = np.unique(X[feature], return_counts=True)weighted_gini = 0for v, c in zip(values, counts):subset_y = y[X[feature] == v]weighted_gini += (c / len(y)) * self._gini(subset_y)return weighted_ginidef _choose_best_feature(self, X, y, features):"""選擇最佳分裂特征"""gini_indices = [self._gini_index(X, y, f) for f in features]best_idx = np.argmin(gini_indices)return features[best_idx]def _build_tree(self, X, y, features, depth=0):"""遞歸構建決策樹"""# 終止條件if (len(np.unique(y)) == 1 or(self.max_depth is not None and depth >= self.max_depth) orlen(y) < self.min_samples_split):return {'class': Counter(y).most_common(1)[0][0]}# 選擇最佳特征best_feature = self._choose_best_feature(X, y, features)tree = {'feature': best_feature, 'children': {}}# 遞歸構建子樹remaining_features = [f for f in features if f != best_feature]for value in np.unique(X[best_feature]):subset_X = X[X[best_feature] == value].drop(columns=[best_feature])subset_y = y[X[best_feature] == value]tree['children'][value] = self._build_tree(subset_X, subset_y, remaining_features, depth + 1)return treedef fit(self, X, y):"""訓練模型"""# 將分類特征轉換為數值（簡化實現）self.label_encoders = {}X_encoded = X.copy()for col in X.columns:le = {val: idx for idx, val in enumerate(X[col].unique())}X_encoded[col] = X[col].map(le)self.label_encoders[col] = ley_encoded = y.map({'否': 0, '是': 1})self.tree = self._build_tree(X_encoded, y_encoded, X.columns.tolist())def predict(self, X):"""預測"""X_encoded = X.copy()for col in X.columns:X_encoded[col] = X[col].map(self.label_encoders[col])predictions = []for _, row in X_encoded.iterrows():node = self.treewhile 'children' in node:feature = node['feature']value = row[feature]if value in node['children']:node = node['children'][value]else:breakpredictions.append(node.get('class', 0))return ['是' if p == 1 else '否' for p in predictions]

通過遞歸地選擇基尼指數最小的特征進行節點分裂，構建二叉樹結構的決策模型。

主要流程分為四個關鍵步驟：

1) 數據預處理階段將分類特征編碼為數值形式；

2) 計算各特征的基尼指數，選擇使數據不純度降低最多的特征作為分裂節點；

3) 遞歸構建決策樹，直到滿足終止條件（節點樣本純凈、達到最大深度或樣本數不足）；

4) 預測時根據特征值匹配樹的分支結構，最終到達葉節點獲得分類結果。該實現完整體現了CART算法的核心特點：使用基尼指數作為分裂標準、支持預剪枝參數控制過擬合、采用字典嵌套結構存儲樹形關系，并能處理分類特征，最終輸出"是"/"否"的貸款審批決策。

main.py

import numpy as npfrom data_loader import load_data
from c45_tree import C45DecisionTree
from cart_tree import CARTDecisionTreedef accuracy(y_true, y_pred):return np.sum(y_true == y_pred) / len(y_true)def print_tree(node, feature_names, class_names, indent=""):"""打印決策樹結構"""if 'class' in node:print(indent + "預測:", class_names[node['class']])else:print(indent + "特征:", feature_names[node['feature']] if isinstance(node['feature'], int) else node['feature'])for value, child in node['children'].items():print(indent + f"--> 值: {value}")print_tree(child, feature_names, class_names, indent + "    ")if __name__ == "__main__":# 加載數據X_train, X_test, y_train, y_test, feature_names = load_data()class_names = ['否', '是']# 訓練和評估C4.5print("\n=== C4.5決策樹 ===")c45 = C45DecisionTree(max_depth=3)c45.fit(X_train, y_train)print("測試集準確率:", accuracy(y_test, c45.predict(X_test)))print("\n決策樹結構:")print_tree(c45.tree, feature_names, class_names)# 訓練和評估CARTprint("\n=== CART決策樹 ===")cart = CARTDecisionTree(max_depth=3)cart.fit(X_train, y_train)print("測試集準確率:", accuracy(y_test, cart.predict(X_test)))print("\n決策樹結構:")print_tree(cart.tree, feature_names, class_names)