機器學習（神經網絡基礎篇）——個人理解篇6(概念+代碼)

1 在聲明一個類中，構建一個屬于類的函數，前面為什要加上“self”？

就像下面這一串代碼：

 class TwoLayerNet:def __init__(self, input_size, hidden_size, output_size,weight_init_std=0.01):# 
初始化權重self.params = {}self.params['W1'] = weight_init_std * \np.random.randn(input_size, hidden_size)self.params['b1'] = np.zeros(hidden_size)self.params['W2'] = weight_init_std * \np.random.randn(hidden_size, output_size)self.params['b2'] = np.zeros(output_size)def predict(self, x):W1, W2 = self.params['W1'], self.params['W2']b1, b2 = self.params['b1'], self.params['b2']a1 = np.dot(x, W1) + b1z1 = sigmoid(a1)a2 = np.dot(z1, W2) + b2y = softmax(a2)return y

解釋：

在Python中，self 是一個指向當前類實例自身的引用參數，它的作用類似于“我”或“這個對象”。它的存在是為了讓類的方法（函數）能夠訪問和操作這個實例的屬性（變量）和其他方法。

專業解釋：

1 訪問實例屬性
在 predict 方法中，你需要訪問當前實例的權重參數 self.params['W1']、self.params['b1'] 等。沒有 self，方法就不知道去哪里找這些參數。
2 區分不同實例
如果有多個神經網絡實例（比如 net1 和 net2），它們的權重參數是獨立的。通過 self，每個實例的方法只會操作自己的參數，不會互相干擾。

通俗解釋：
想象你有一個機器人（類 TwoLayerNet），它身上有多個按鈕（屬性如 params）和功能（方法如 predict）。當你按下某個功能按鈕時，機器人需要知道：“這個功能是針對 我自身 的哪些屬性操作的？”這時 self 就是告訴機器人：“操作的是當前這個機器人自己的按鈕，而不是其他機器人的。”

總結：self 是類方法的“自我標識符”，讓方法知道應該操作哪個實例的數據。沒有它，類的方法就無法區分不同實例的屬性。

2? ?神經網絡中的參數優化，你知道哪些？有什么優缺點？（純個人總結）

所謂優化，實質上是找使得損失函數的值最小的一組參數。舉一個生活中的例子：

2.1? ?用調熱水澡水溫類比神經網絡參數優化

想象你正在調整淋浴的冷熱水龍頭，目標是找到 ?最舒適的水溫。這個過程與神經網絡的參數優化驚人地相似：

1. 初始狀態（參數初始化）??

?場景?：第一次打開淋浴，隨機擰動冷熱龍頭（初始權重和偏置隨機設置）。
?結果?：水溫要么太冷（預測錯誤），要么太燙（損失函數值大）。

2. 試水溫（前向傳播）??

?動作?：伸手試水溫，感受冷熱程度。
?對應?：
- 輸入數據 = 當前冷熱水比例（參數）
- 輸出結果 = 實際水溫（預測值）
- 目標 = 理想水溫（標簽）
- 誤差 = 水溫偏差（損失函數值）

3. 調整龍頭（反向傳播與梯度下降）??

?冷熱不均（計算梯度）??：
- 若水太冷 → ?需要更多熱水?（梯度指向增加熱水權重的方向）。
- 若水太熱 → ?需要更多冷水?（梯度指向減少熱水權重的方向）。
- 調整幅度 = 手擰龍頭的力度（學習率）。
?具體操作?：
- 微調熱水龍頭開大一點（參數更新公式：W = W - 學習率 × 梯度）。
- 下次再試水溫（下一輪訓練）。

4. 反復調試（迭代優化）??

?過程?：
太冷 → 加熱水 → 試水 → 太燙 → 減熱水 → 試水 → 接近舒適 → 微調...
?對應?：
通過多次迭代（epoch），參數（冷熱水比例）逐漸收斂到最佳值（損失函數最小化）。

5. 成功（模型收斂）??

?結果?：水溫穩定在理想溫度（模型準確預測）。
?關鍵因素?：
- ?學習率?：手擰龍頭的幅度太大（學習率高）→ 水溫反復震蕩；幅度太小（學習率低）→ 調整過慢。
- ?耐心（迭代次數）??：足夠多的調試次數才能找到平衡點。

2.2? ? ?SGD（隨機下降）介紹

1? ?核心公式：

這里把需要更新的權重參數記為W，把損失函數關于W的梯度記為。 η表示學習率，實際上會取0.01或0.001這些事先決定好的值。上式中的←表示用右邊的值更新左邊的值。（可以理解為朝向梯度下降的方向前進）

2? ?SGD缺點：

首先來求的最值問題。

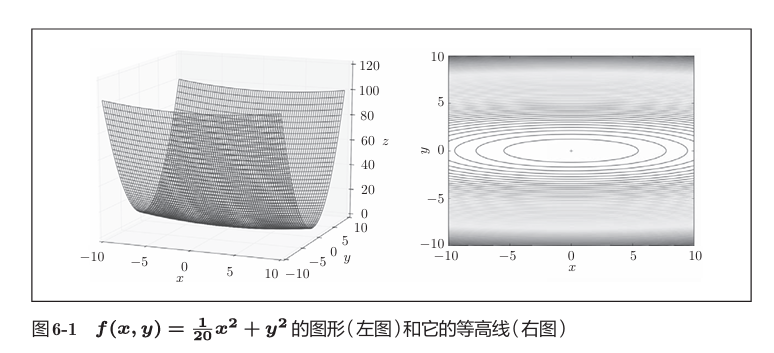
左圖表示的函數是向x軸方向延伸的“碗”狀函數。右圖是等高線呈向x軸方向延伸的橢圓狀。

此函數對應的梯度如下圖：

這個梯度的特征是，y軸方向上大，x軸方向上小。換句話說，就是y軸方向的坡度大，而x軸方向的坡度小。假設從（x , y ）=（-7, 2）處（初始值）開始搜索，結果如下圖所示：

如圖，雖然最后能找到“最優點”，但是過程很曲折，，SGD呈“之”字形移動。這是一個相當低效的路徑，在Y軸上跨度比較大，但是在水平方向上看，每次平移的：“步伐”總是很小。

為了改正SGD的缺點，下面將介紹Momentum、AdaGrad、Adam這3 種方法來取代SGD。

2.3?　Momentum（同SGD相比，引入了阻力下的初始速度）

Momentum是“動量”的意思，和物理有關。

1? ?我個人的理解：

將二維空間圖像的梯度進行正交分解，在梯度跨度大的方向（比如Y軸）對梯度的跨度進行適當的“動態調整”，在梯度跨度小的方向（比如X軸）對梯度的跨度施加外力作用，“迫使”梯度跨度逐漸增加。

2? 核心公式：

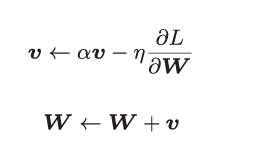
和前面的SGD一樣，W表示要更新的權重參數，表示損失函數關于W的梯度，η表示學習率。這里新出現了一個變量v，對應物理上的速度。

例如下圖：

αv這一項，在物體不受任何力時，該項承擔使物體逐漸減速的任務（α設定為0.9之類的值），對應物理上的地面摩擦或空氣阻力。

class Momentum:def __init__(self, lr , moment):self.lr = lrself.moment = momentself.v = Nonedef update (self, para , grad):if self.v is None:self.v = {}for key , val in para.items():self.v[key] = np.zeros_like(val)for key in para.keys():para[key] = self.moment * self.v[key] - self.lr - grad[key]para[key] =+ self.v[key]

實例變量v會保存物體的速度。初始化時，v中什么都不保存，但當第一次調用update()時，v會以字典型變量的形式保存與參數結構相同的數據。

假設采用Momentum解決函數最優化的問題，相應的優化路徑如下：

? ??

和SGD相比，我們發現 “之”字形的“程度”減輕了。這是因為雖然x軸方向上受到的力非常小，但是一直在同一方向上受力，所以朝同一個方向會有一定的加速。反過來，雖然y軸方向上受到的力很大，但是因為交互地受到正方向和反方向的力，它們會互相抵消，所以y軸方向上的速度不穩定。因此，和SGD時的情形相比，可以更快地朝x軸方向靠近，減弱“之”字形的變動程度。

2.4? ? AdaGrad

在神經網絡的學習中，學習率（數學式中記為η）的值很重要。學習率過小，會導致學習花費過多時間；反過來，學習率過大，則會導致學習發散而不能正確進行。

有一種被稱為學習率衰減（learning rate decay）的方法，即隨著學習的進行，使學習率逐漸減小。

AdaGrad會為參數的每個元素適當地調整學習率。

1? 核心公式：

和前面的SGD一樣，W表示要更新的權重參數，表示損失函數關于W的梯度，η表示學習率。這里新出現了變量h，它保存了以前的所有梯度值的平方和（表示對應矩陣元素的乘法）。然后，在更新參數時，通過乘以，就可以調整學習的尺度。這意味著，參數的元素中變動較大（被大幅更新）的元素的學習率將變小。也就是說，可以按參數的元素進行學習率衰減，使變動大的參數的學習率逐漸減小。

AdaGrad代碼實現過程：

class AdaGrad:def __init_(self, lr = 0.01):self.lr = lrself.h = Nonedef update(self, para, grad):if self.h is None:self.h = {}for key, val in para.items():self.h[key] = np.zeros_like(val)for key in para.keys():self.h[key] += grad[key] * grad[key]para[key] -= self.lr * grad[key] / (np.sqrt(self.h[key]) + 1e-7)

假設采用AdaGrad解決函數最優化的問題，相應的優化路徑如下：