【深度學習與實戰】2.3、線性回歸模型與梯度下降法先導案例--最小二乘法(向量形式求解)

為了求解損失函數? $loss = (f(x)-y)^2 = (wx-y)^2$ 對? $w$ ?的導數，并利用最小二乘法向量形式求解? $w$ ?的值?

這是?線性回歸?的平方誤差損失函數，目標是最小化預測值? $X_w$ ?與真實值? $y$ ?之間的差距。

?損失函數?：
考慮多個樣本的情況，損失函數為所有樣本的平方誤差之和：

$L = (Xw-Y)^2$

?????????????????????? $=( X w-Y )^{\top} ( X w-Y )$

????????????????????????????????????????????????????????? $=w^{\mathsf{T}} X^{\mathsf{T}} X w-Y^{\mathsf{T}} X w-w^{\mathsf{T}} X^{\mathsf{T}} Y+Y^{\mathsf{T}} Y$

$L$ ?是損失函數
$X$ ?是? $n\times m$ ?的設計矩陣（ $n$ 個樣本， $m$ 個特征）。
$w$ 是? $m\times 1$ ?的權重向量。
$Y$ 是? $n\times 1$ ?的目標值向量。
對于兩個列向量 $\partial$ 和 $b$ ，它們的點積（內積）就是 $\partial ^Tb$ ,?? $\partial ^T$ 是向量? $\partial$ ?的轉置

針對? $f(x)$ ? $=w^{\mathsf{T}} X^{\mathsf{T}} X w-Y^{\mathsf{T}} X w-w^{\mathsf{T}} X^{\mathsf{T}} Y+Y^{\mathsf{T}} Y$ 函數求導，有一下性質：

$\frac{\partial AB}{\partial B} = A^T,\frac{\partial A^TB}{\partial A} = B,\frac{\partial C^TAC}{\partial C} = 2AC$

對每項求導?

?第一項? ? $w^{\mathsf{T}} X^{\mathsf{T}} X w$

????????將? $\frac{\partial C^TAC}{\partial C} = 2AC$ ?公式代入得

???????? $X^T \cdot w^T X w$ ?? $\Rightarrow$ ?? $X^T\cdot 2AC$ ? $\Rightarrow$ ? $2X^TXw$

???????? $w^{\mathsf{T}} X^{\mathsf{T}} X w$ ?? $= 2X^TXw$

????????其中?? $w^T$ ? 為? $C^T$ ,? $X$ ?為? $A$ ， $w$ ?為? $c$ 。

第二項?? $Y^{\mathsf{T}} X w$

????????將? $\frac{\partial AB}{\partial B} = A^T$ ?公式代入得

? ? ? ? $Y^{\mathsf{T}} X \cdot w\Rightarrow A^T \Rightarrow (Y^{\mathsf{T}} X)^T$

????????? $Y^{\mathsf{T}} X w = (Y^{\mathsf{T}} X)^T$

????????其中? $Y^{\mathsf{T}} X$ ?為? $A$ , $w$ ?為? $B$

第三項? $w^{\mathsf{T}} X^{\mathsf{T}} Y$

????????將? $\frac{\partial A^TB}{\partial A} = B$ ?代入得

???????? $w^{\mathsf{T}} \cdot X^{\mathsf{T}} Y\Rightarrow B\Rightarrow X^{\mathsf{T}} Y$

???????? $w^{\mathsf{T}} X^{\mathsf{T}} Y = X^{\mathsf{T}} Y$

????????其中? $w^T$ ?為? $A^T$ , $X^{\mathsf{T}} Y$ ?為? $B$

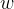第四項沒有? $w$ ?看作常數項常數項的導數為0

合并項得

???????? $f(x) =w^{\mathsf{T}} X^{\mathsf{T}} X w-Y^{\mathsf{T}} X w-w^{\mathsf{T}} X^{\mathsf{T}} Y+Y^{\mathsf{T}} Y$

? ? ? $= 2X^TXw-(Y^{\mathsf{T}} X)^T-X^{\mathsf{T}} Y+0$

$=2X^TXw-X^{\mathsf{T}} Y-X^{\mathsf{T}} Y$ ? ? ? ? ?

$=2X^TXw-2X^{\mathsf{T}} Y$ ? ? ? ? ? ? ? ? ? ? ??

$=2(X^TXw-X^{\mathsf{T}} Y)$ ? ? ? ? ? ? ? ? ?? ??

?令? $\frac{\partial f(w)}{\partial w} = 0$ ,得

? $2(X^TXw-X^{\mathsf{T}} Y) = 0$

$X^TXw=X^{\mathsf{T}} Y$

$(X^TX)^{-1}X^TXw=(X^TX)^{-1}X^{\mathsf{T}} Y$ ?（ $X^TX$ ?可逆時）

$w=(X^TX)^{-1}X^{\mathsf{T}} Y$

$(X^TX)$ 和 $(X^TX)^{-1}$ 互為逆矩陣?? $(X^TX)(X^TX)^{-1} = 1$

得出結果

??? $w=(X^TX)^{-1}X^{\mathsf{T}} Y$

解釋：

$(X^TX)(X^TX)^{-1} = 1$ , $(X^TX)$ 與 $(X^TX)^{-1}$ 互逆

?逆矩陣的定義

如果? $B$ 是? $A$ 的逆矩陣，則滿足：

$AB=BA=I$ (單位矩陣類似于數值乘法中的?1)

?即無論? $A$ 左乘還是右乘? $B$ ，結果均為單位矩陣。

必要條件?

$A$ 和 $B$ 必須是方陣（行數=列數）

$A$ 必須可逆（即行列式 $det(A) \neq 0$ ）

直觀理解

?逆矩陣的作用類似于“倒數”。例如，數值中? $2\times \frac{1}{2} = 1$ ，類似地，矩陣中? $A\times A^{-1} = I$ 。

單位矩陣? $I$ 在矩陣乘法中的作用類似于數值乘法中的?1。

示例驗證

取矩陣? $A=\begin{bmatrix} 1 & 2 \\ 3& 4 \end{bmatrix}$ ，其行列式 $det(A) = -2 \neq 0$ ，故可逆。

計算逆矩陣：

$A^{-1} = \frac{1}{det(A)}\begin{bmatrix} 4 &-2 \\ -3& 1 \end{bmatrix}= \frac{1}{-2}\begin{bmatrix} 4 &-2 \\ -3& 1 \end{bmatrix}= \begin{bmatrix} -2 &1 \\ \frac{3}{2}& -\frac{1}{2} \end{bmatrix}$

?(1) 第一行第一列的元素 ( $C_{11}$ ?)?

$C_{11}=\frac{1}{-2}\times 4=-2$

?(2) 第一行第二列的元素 ( $C_{12}$ ?)?

$C_{12}=\frac{1}{-2}\times -2 = 1$

?(3) 第一行第二列的元素 ( $C_{21}$ ?)?

$C_{21}=\frac{1}{-2}\times -3 = \frac{3}{2}$

?(4) 第一行第二列的元素 ( $C_{22}$ ?)?

$C_{22}=\frac{1}{-2}\times 1 =- \frac{1}{2}$

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/web/73506.shtml
繁體地址，請注明出處：http://hk.pswp.cn/web/73506.shtml
英文地址，請注明出處：http://en.pswp.cn/web/73506.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！