歸并排序

算法思路

歸并排序算法有兩個基本的操作，一個是分，也就是把原數組劃分成兩個子數組的過程。另一個是治，它將兩個有序數組合并成一個更大的有序數組。

將待排序的線性表不斷地切分成若干個子表，直到每個子表只包含一個元素，這時，可以認為只包含一個元素的子表是有序表。
將子表兩兩合并，每合并一次，就會產生一個新的且更長的有序表，重復這一步驟，直到最后只剩下一個子表，這個子表就是排好序的線性表。

代碼

// 歸并排序
public int[] sortArray(int[] nums) {return mergeSort(nums, 0, nums.length - 1);
}private int[] mergeSort(int[] nums, int left, int right) {// 遞歸終止條件if (left >= right) {// 返回單個元素的數組return new int[]{nums[left]};}// 分治int mid = (left 0+ right) / 2;// 分別對左右子數組進行排序int[] leftArr = mergeSort(nums, left, mid);int[] rightArr = mergeSort(nums, mid + 1, right);int[] res = new int[leftArr.length + rightArr.length];// 合并兩個有序數組int i = 0, j = 0, k = 0;while (i < leftArr.length && j < rightArr.length) {if (leftArr[i] <= rightArr[j]) {res[k++] = leftArr[i++];} else {res[k++] = rightArr[j++];}}while (i < leftArr.length) {res[k++] = leftArr[i++];}while (j < rightArr.length) {res[k++] = rightArr[j++];}return res;
}

時間復雜度

O(nlogn)

堆排序

什么是堆？

如下圖（大根堆）（二叉）堆是一個數組，它可以被看成一個完全二叉樹。
二叉樹形式：

數組形式：

堆的根節點在數組中的下標為0，我們很容易得到左孩子為1，右孩子為2，第i個節點的左孩子為2i+1，右孩子為2i+2 。
二叉堆分為兩種形式：大根堆和小根堆。大根堆性質，根節點的值大于所以子樹節點的值。小根堆性質，根節點的值小于所以子樹節點的值。

如何維護堆？

Java代碼維護大根堆：

//維護大根堆
private void heapify(int n,int i) {//當前根節點int largest = i;//左孩子節點int lchild = 2*i+1;//右孩子節點int rchild = 2*i+2;//找三個元素最大的作為父節點if (lchild < n && nums[lchild] > nums[largest]) {largest = lchild;}if (rchild < n && nums[rchild] > nums[largest]) {largest = rchild;}//如果交換則維護交換后的if (largest != i) {swap(largest,i);heapify(n,largest);}
}

問題：為啥交換后，只需要維護交換后的子節點呢？
舉一個例子：

根節點需要跟左孩子交換，交換后，根節點的右子樹并未改變樹結構，則只需要遞歸維護根節點左子樹的堆性質。

如何建堆？

我們可以用自低向上的方法利用上面維護堆的算法heapify來建堆。子數組從n/2開始都是樹的葉子節點。每個葉子節點可以被看成包含一個元素的堆。所以建堆的過程從n/2-1–>0 。

//1.建堆//從最后一個有孩子的節點開始 n/2-1for (int i = n/2-1; i >= 0; i--) {heapify(n,i);}

堆排序

前面我們利用建堆算法成功建立一個大根堆。因為數組最大元素總在根節點nums[0]中，通過把它與nums[n-1]交換，我們可以讓該元素放到正確的位置。這時候，如果我們從堆中去掉節點n-1，剩余節點中根的孩子結點仍然是大根堆，而新的根節點可能違背大根堆性質。為了維護大根堆性質，需要不斷調用 heapify 從而在nums 上構建一個新的大根堆。堆排序算法會不斷重復這個過程，直到堆的大小從n-1降到1 。

給出完整的堆排序算法：

private int[] nums;// 待排序數組
//堆排序									
private void heap_sort(int n) {//1.建堆//從最后一個有孩子的節點開始 n/2-1for (int i = n/2-1; i >= 0; i--) {heapify(n,i);}//2.堆排序for (int i = n-1; i > 0; i--) {swap(i,0);//交換最后一個和根元素heapify(i,0);//交換后維護}
}
//維護大根堆
private void heapify(int n,int i) {int largest = i;int lchild = 2*i+1;int rchild = 2*i+2;//找三個元素最大的作為父節點if (lchild < n && nums[lchild] > nums[largest]) {largest = lchild;}if (rchild < n && nums[rchild] > nums[largest]) {largest = rchild;}//如果交換則維護交換后的if (largest != i) {swap(largest,i);heapify(n,largest);}
}private void swap(int i,int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;
}

時間復雜度

O(nlogn)

快速排序

算法思想

通過一趟排序將要排序的數據分割成獨立的兩部分，其中一部分的所有數據都比另外一部分的所有數據都要小，然后再按此方法對這兩部分數據分別進行快速排序，整個排序過程可以遞歸進行，以此達到整個數據變成有序序列。
快速排序算法通過多次比較和交換來實現排序，其排序流程如下：

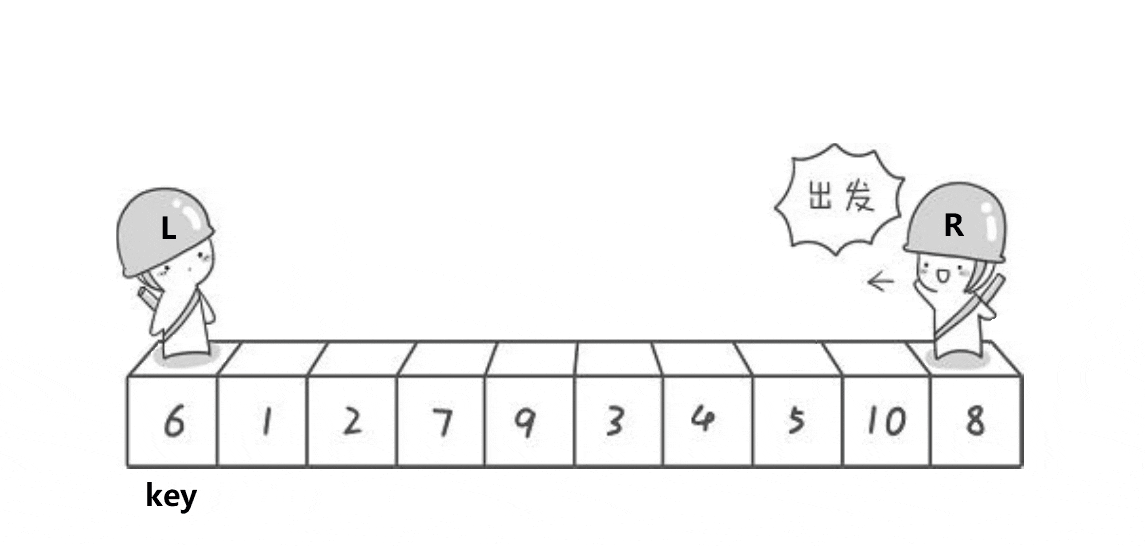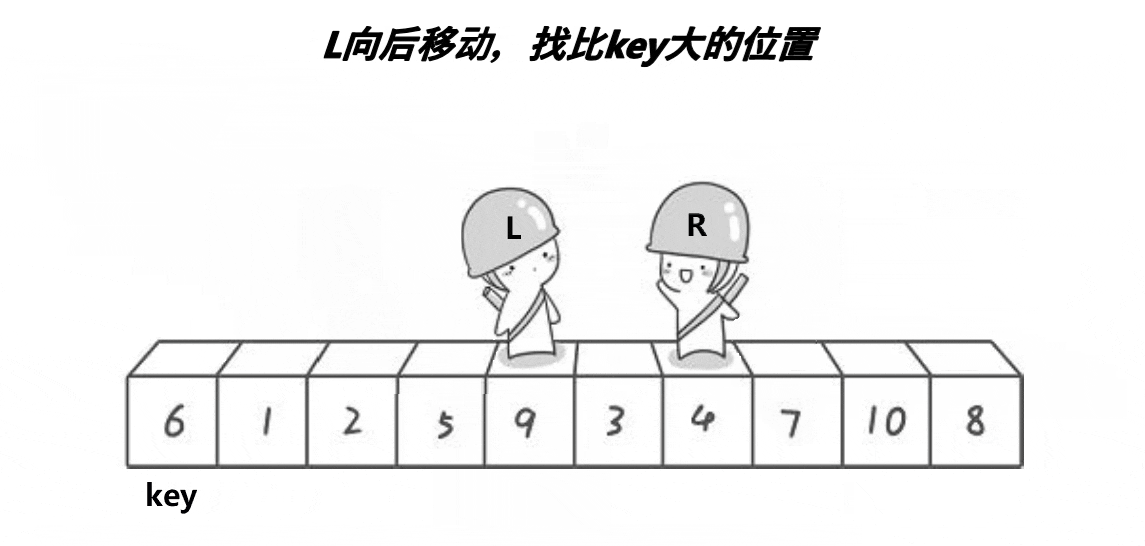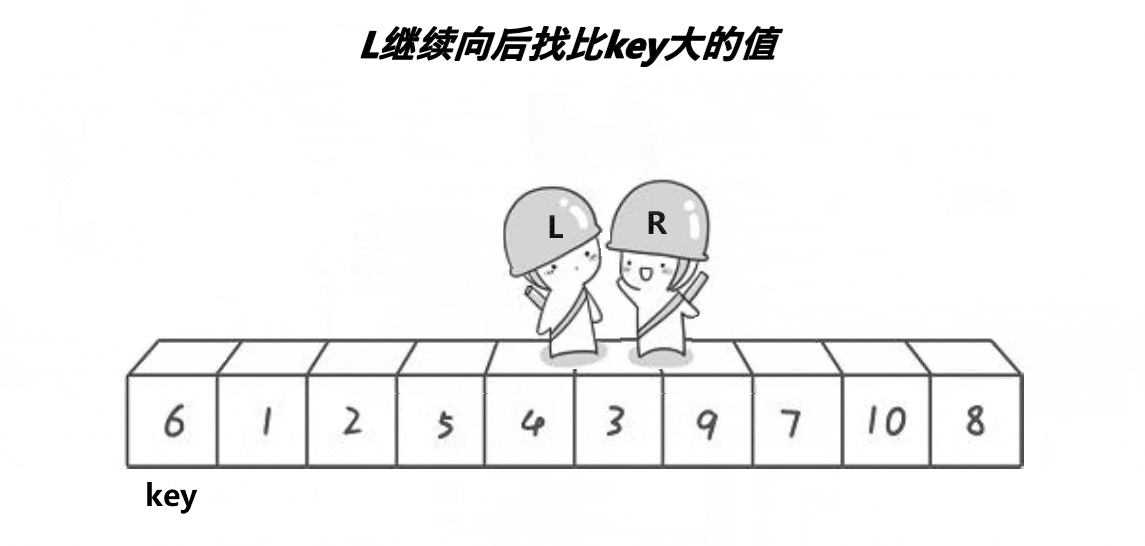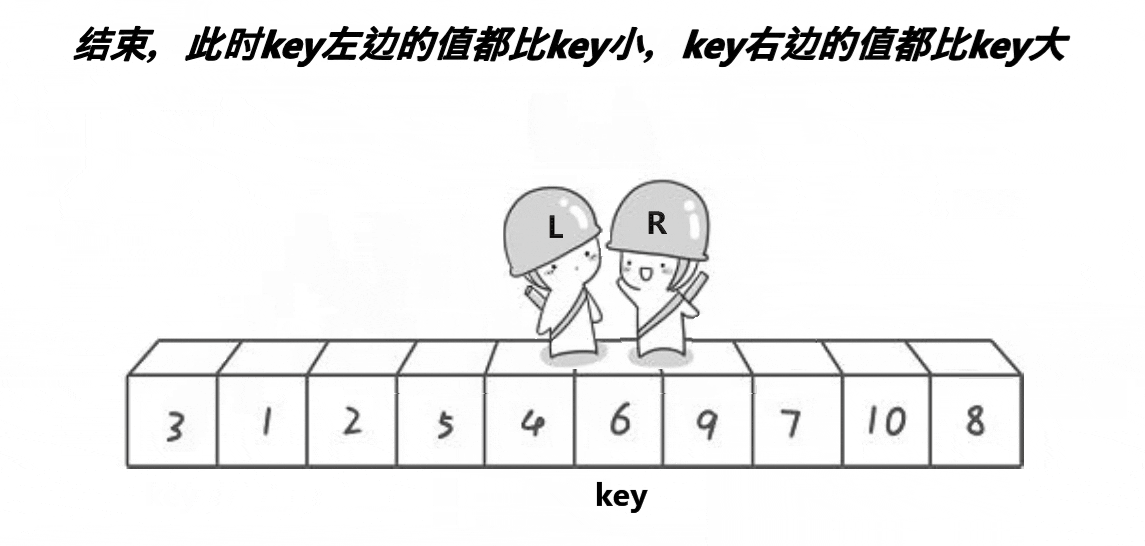
1、首先設定一個基數，通過該基數將數組分成左右兩部分。

2、將大于或等于基數的數據集中到數組右邊，小于基數的數據集中到數組的左邊。此時，左邊部分中各元素都小于或等于基數，而右邊部分中各元素都大于或等于基數。

3、然后，左邊和右邊的數據可以獨立排序。對于左側的數組數據，又可以取一個基數，將該部分數據分成左右兩部分，同樣在左邊放置較小值，右邊放置較大值。右側的數組數據也可以做類似處理。

4、重復上述過程，可以看出，這是一個遞歸定義。通過遞歸將左側部分排好序后，再遞歸排好右側部分的順序。當左、右兩個部分各數據排序完成后，整個數組的排序也就完成了。

概括來說為 挖坑填數 + 分治法。

代碼

代碼中使用Random作為隨機生成器生成基數，思想不變，只是基數選取的方式改變。

private int[] nums;
// 隨機數生成器, 用于生成選擇基數元素
private final Random random = new Random();public int[] sortArray(int[] nums) {this.nums = nums;quickSort(0, nums.length - 1);return nums;
}
public void quickSort(int left, int right) {// 遞歸終止條件if (left >= right) {return;}// 調用partition函數，對數組進行分區，并獲取基準元素的最終位置int pivot = partition(left, right);// 遞歸調用，對左子數組進行快速排序quickSort(left, pivot - 1);// 遞歸調用，對右子數組進行快速排序quickSort(pivot + 1, right);
}
public int partition(int left, int right) {// 生成一個隨機的基準元素位置int pivot = random.nextInt(right - left + 1) + left;// 保存基準元素的值int pivotVal = nums[pivot];// 將基準元素交換到數組的最后一個位置swap(pivot, right);// 定義兩個指針，i指向數組的最左邊，j指向數組的最右邊int i = left, j = right;while (i < j) {// 從左向右找到第一個大于等于基準元素的位置while (i < j && nums[i] <= pivotVal) {i++;}// 從右向左找到第一個小于等于基準元素的位置while (i < j && nums[j] >= pivotVal) {j--;}// 如果i和j指向的位置不合法，則交換i和j指向的元素if (i < j) {swap(i, j);}}// 將基準元素交換到正確的位置swap(i, right);return i;
}public void swap(int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;
}

時間復雜度

O(nlogn)