目錄
5.4.2樹、森林與二叉樹的轉換
1.樹轉換為二叉樹
【樹和二叉樹的轉換及相關性質的推理(2009、2011)】
2.森林轉換為二叉樹
【森林和二叉樹的轉換及相關性質的推理(2014)】
3.二叉樹轉換為森林
【由遍歷序列構造一棵二叉樹并轉換為對應的森林(2020、2021)】
5.4.3樹和森林的遍歷
1.樹的遍歷
【樹與二叉樹遍歷方法的對應關系(2019)】
2.森林的遍歷
【森林與二叉樹遍歷方法的對應關系(2020)】
5.4.2樹、森林與二叉樹的轉換
1.樹轉換為二叉樹
【樹和二叉樹的轉換及相關性質的推理(2009、2011)】
樹轉換為二叉樹的規則:每個結點的左指針指向它的第一個孩子,右指針指向它在樹中的相鄰右兄弟,這個規則又稱“左孩子右兄弟”。由于根結點沒有兄弟,因此樹轉換得到的二叉樹沒有右子樹,如圖 5.23 所示。

樹轉換為二叉樹的畫法:
1) 在兄弟結點之間加一連線;
2) 對每個結點,只保留它與第一個孩子的連線,而與其他孩子的連線全部抹掉:
3) 以樹根為軸心,順時針旋轉 45°。
2.森林轉換為二叉樹
【森林和二叉樹的轉換及相關性質的推理(2014)】
將森林轉換為二叉樹的規則與樹類似。先將森林中的每棵樹轉換為二叉樹,由于任意一棵樹對應的二叉樹的右子樹必空,若把森林中第二棵樹根視為第一棵樹根的右兄弟,即將第二棵樹對應的二叉樹當作第一棵二叉樹根的右子樹,將第三棵樹對應的二叉樹當作第二棵二叉樹根的右子樹,以此類推,就可以將森林轉換為二叉樹。
森林轉換為二叉樹的畫法:
1) 將森林中的每棵樹轉換成相應的二叉樹;
2) 每棵樹的根也可視為兄弟關系,在每棵樹的根之間加一根連線:
3) 以第一棵樹的根為軸心順時針旋轉 45°。
3.二叉樹轉換為森林
【由遍歷序列構造一棵二叉樹并轉換為對應的森林(2020、2021)】
二叉樹轉換為森林的規則:
若二叉樹非空,則二叉樹的根及其左子樹為第一棵樹的二叉樹形式,所以將根的右鏈斷開。
二叉樹根的右子樹又可視為一個由除第一棵樹外的森林轉換后的二叉樹,應用同樣的方法,直到最后只剩一棵沒有右子樹的二叉樹為止,最后將每棵二叉樹依次轉換成樹,就得到了原森林,如圖5.24所示。二叉樹轉換為樹或森林是唯一的。
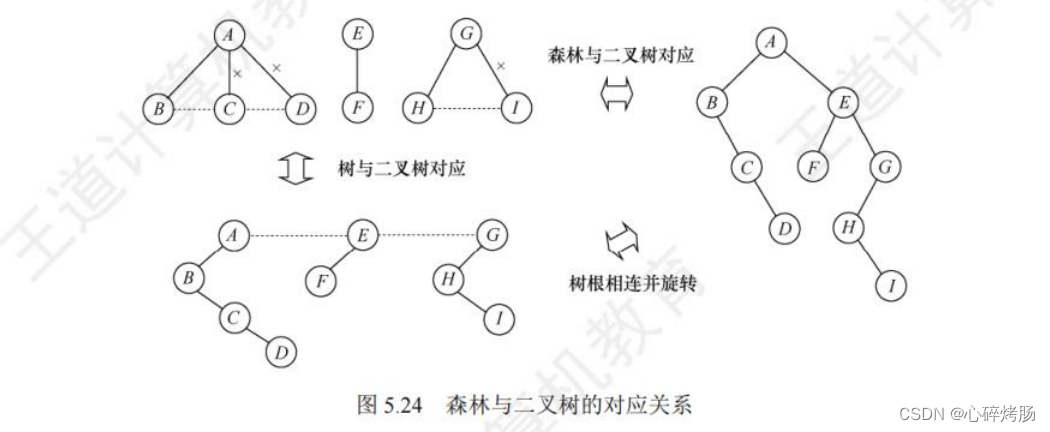
5.4.3樹和森林的遍歷
1.樹的遍歷
【樹與二叉樹遍歷方法的對應關系(2019)】
樹的遍歷是指用某種方式訪問樹中的每個結點,且僅訪問一次。主要有兩種方式:
1) 先根遍歷。若樹非空,則按如下規則遍歷:
- 先訪問根結點。
- 再依次遍歷根結點的每棵子樹,遍歷子樹時仍遵循先根后子樹的規則
其遍歷序列與這棵樹相應二叉樹的先序序列相同。
2) 后根遍歷。若樹非空,則按如下規則遍歷:
- 先依次遍歷根結點的每棵子樹,遍歷子樹時仍遵循先子樹后根的規則。
- 再訪問根結點。
其遍歷序列與這棵樹相應二叉樹的中序序列相同。
圖5.23 的樹的先根遍歷序列為ABEFCDG,后根遍歷序列為 EFBCGDA。
另外,樹也有層次遍歷,與二叉樹的層次遍歷思想基本相同,即按層序依次訪問各結點。
2.森林的遍歷
按照森林和樹相互遞歸的定義,可得到森林的兩種遍歷方法。
1) 先序遍歷森林。若森林為非空,則按如下規則遍歷:
- 訪問森林中第一棵樹的根結點。
- 先序遍歷第一棵樹中根結點的子樹森林。
- 先序遍歷除去第一棵樹之后剩余的樹構成的森林。
2) 中序遍歷森林。森林為非空時,按如下規則遍歷:
- 中序遍歷森林中第一棵樹的根結點的子樹森林。
- 訪問第一棵樹的根結點。
- 中序遍歷除去第一棵樹之后剩余的樹構成的森林。
圖5.24的森林的先序遍歷序列為ABCDEFGHI,中序遍歷序列為 BCDAFEHIG。
【森林與二叉樹遍歷方法的對應關系(2020)】
當森林轉換成二叉樹時,其第一棵樹的子樹森林轉換成左子樹,剩余樹的森林轉換成右子樹,可知森林的先序和中序遍歷即為其對應二叉樹的先序和中序遍歷。
樹和森林的遍歷與二叉樹的遍歷關系見表。
| 樹 | 森林 | 二叉樹 |
| 先根遍歷 | 先序遍歷 | 先序遍歷 |
| 后根遍歷 | 中序遍歷 | 中序遍歷 |
注意:部分教材也將森林的中序遍歷稱為后序遍歷,稱中序遍歷是相對其二叉樹而言的,稱后序遍歷是因為根確實是最后才訪問的,若遇到這兩種稱謂,則可理解為同一種遍歷方法。
















)


