算法：二叉樹相關

題目一：單值二叉樹

題目二：二叉樹的最大深度

題目三：相同的樹

題目四：對稱二叉樹

題目五：另一棵樹的子樹

題目六：二叉樹的前序遍歷

題目七：二叉樹遍歷

題目八：根據二叉樹創建字符串

題目九：二叉樹的層序遍歷I

題目十：二叉樹的層序遍歷II

題目十一：二叉樹的最近公共祖先

題目十二：搜索二叉樹與雙向鏈表

題目十三：前序與中序遍歷序列構造二叉樹

題目十四：中序與后序遍歷序列構造二叉樹

題目十五：二叉樹的前中后序遍歷（非遞歸實現）

題目一：單值二叉樹

如果二叉樹每個節點都具有相同的值，那么該二叉樹就是單值二叉樹。

只有給定的樹是單值二叉樹時，才返回?true；否則返回?false。

示例 1：

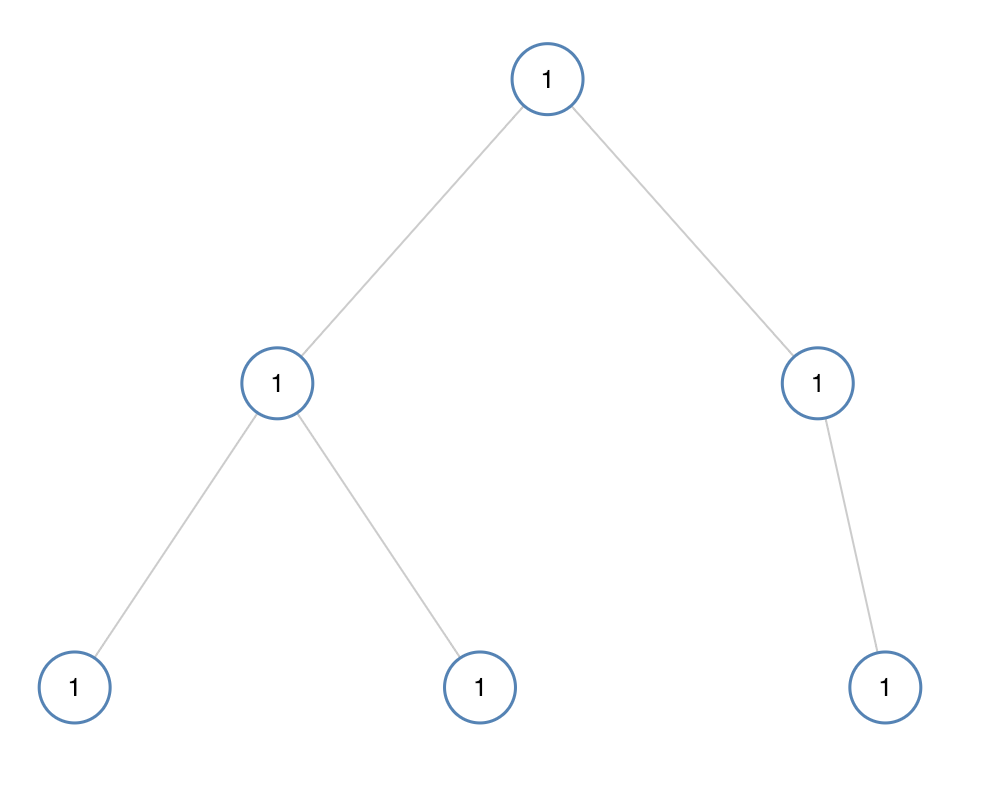
輸入：[1,1,1,1,1,null,1]
輸出：true

示例 2：

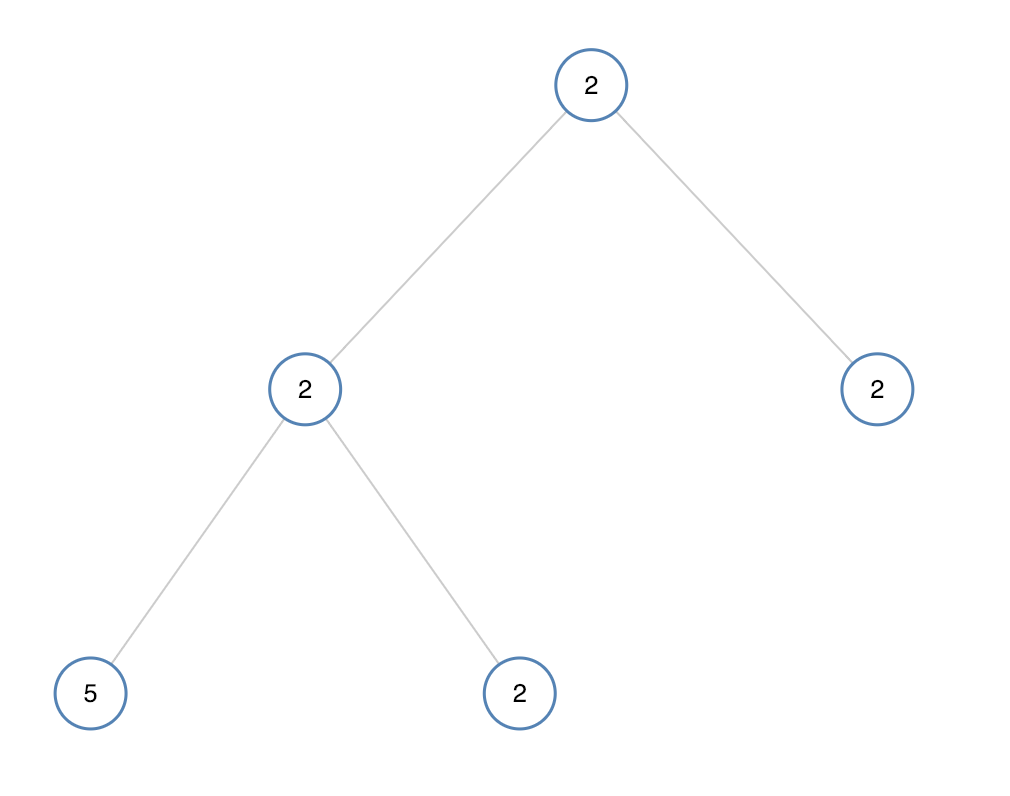
輸入：[2,2,2,5,2]
輸出：false

解法一：拿根結點的值去比較

也就是將root的值傳入，遞歸進二叉樹的左右字樹中，比較是否每個結點都與root的val值相等，如果最終全部相等，就return true，有一個不同，就return false

代碼如下：

class Solution 
{
public:bool _isUnivalTree(TreeNode* root, int val){//開始遞歸遍歷二叉樹的所有結點if(root == nullptr) return true;if(root->val != val) return false;//繼續遍歷左右字樹return _isUnivalTree(root->left, val) && _isUnivalTree(root->right, val);}bool isUnivalTree(TreeNode* root) {if(root == nullptr) return true;int val = root->val;return _isUnivalTree(root, val);}
};

解法二：每次只比較自己的左右孩子

利用傳遞性的原理，每次只比較root和兩個孩子的值是否相同，再繼續往下比，因為如果父親和孩子的val相同，那么父親和孫子的val自然也相同

代碼如下：

class Solution 
{
public:bool isUnivalTree(TreeNode* root) {if(root == nullptr) return true;if(root->left && root->left->val != root->val) return false;if(root->right && root->right->val != root->val) return false;return isUnivalTree(root->left) && isUnivalTree(root->right);}
};

題目二：二叉樹的最大深度

給定一個二叉樹?root?，返回其最大深度。

二叉樹的?最大深度?是指從根節點到最遠葉子節點的最長路徑上的節點數。

示例 1：

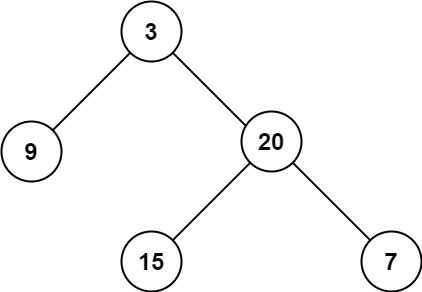
輸入：root = [3,9,20,null,null,15,7]
輸出：3

示例 2：

輸入：root = [1,null,2]
輸出：2

求二叉樹的最大深度，在遞歸時也就是先判斷是否為空，如果不為空就進入左右字樹，此時再左右字樹出來return時需要 + 1，因為只有root結點不為空，才會進入，這里的 + 1 就是加的root結點

代碼如下：

class Solution {
public:int maxDepth(TreeNode* root) {if(root == nullptr) return 0;int left = maxDepth(root->left) + 1;int right = maxDepth(root->right) + 1;return left > right ? left : right;}
};

題目三：相同的樹

給你兩棵二叉樹的根節點?p?和?q?，編寫一個函數來檢驗這兩棵樹是否相同。

如果兩個樹在結構上相同，并且節點具有相同的值，則認為它們是相同的。

示例 1：

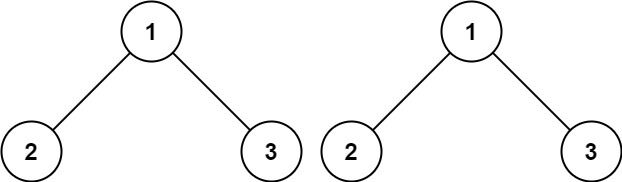
輸入：p = [1,2,3], q = [1,2,3]
輸出：true

示例 2：

輸入：p = [1,2], q = [1,null,2]
輸出：false

示例 3：

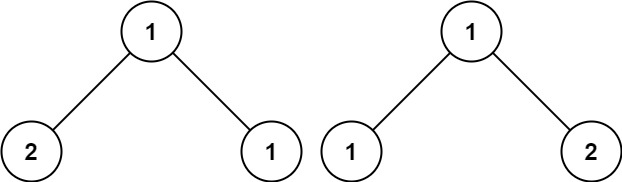
輸入：p = [1,2,1], q = [1,1,2]
輸出：false

這道題就是比較兩個二叉樹是否相等，所以將問題分割為相同的子問題，每次比較當前結點是否相同

如果都為空，那就是true，如果一個為空一個不為空就是false

代碼如下：

class Solution {
public:bool isSameTree(TreeNode* p, TreeNode* q) {//先判斷是否為空if(p == nullptr && q == nullptr) return true;//走到這，說明p和q至少有一個為空，如果進入下面的if語句，說明不同if(p == nullptr || q == nullptr) return false;//接著判斷val值是否相同if(p->val != q->val) return false;//接著進入左子樹和右子樹繼續判斷return isSameTree(p->left, q->left)&& isSameTree(p->right, q->right);}
};

題目四：對稱二叉樹

給你一個二叉樹的根節點?root?，檢查它是否軸對稱。

示例 1：

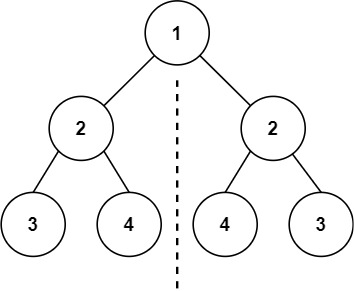
輸入：root = [1,2,2,3,4,4,3]
輸出：true

示例 2：

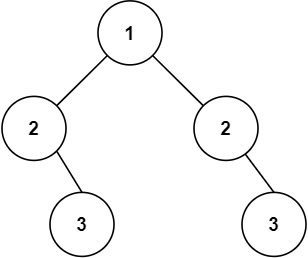
輸入：root = [1,2,2,null,3,null,3]
輸出：false

對稱二叉樹先判斷root是否為空，如果不為空，就判斷左右子樹是否對稱，對稱就是用左子樹的左孩子與右子樹的右孩子比較，不要把比較的對象比較錯了

class Solution {
public:bool _isSymmetric(TreeNode* leftnode, TreeNode* rightnode){if(leftnode == nullptr && rightnode == nullptr)return true;//都為空，返回trueif(leftnode == nullptr || rightnode == nullptr)return false;//一個為空一個不為空，返回falseif(leftnode->val != rightnode->val)return false;//兩個都不為空，但是val值不同，返回false//繼續遞歸左樹的左和右樹的右，因為是對稱的return _isSymmetric(leftnode->left, rightnode->right)&& _isSymmetric(leftnode->right, rightnode->left);} bool isSymmetric(TreeNode* root) {if(root == nullptr) return true;//調用_isSymmetric進行比較root的左右字樹return _isSymmetric(root->left, root->right);}
};

題目五：另一棵樹的子樹

給你兩棵二叉樹?root?和?subRoot?。檢驗?root?中是否包含和?subRoot?具有相同結構和節點值的子樹。如果存在，返回?true?；否則，返回?false?。

二叉樹?tree?的一棵子樹包括?tree?的某個節點和這個節點的所有后代節點。tree?也可以看做它自身的一棵子樹。

示例 1：

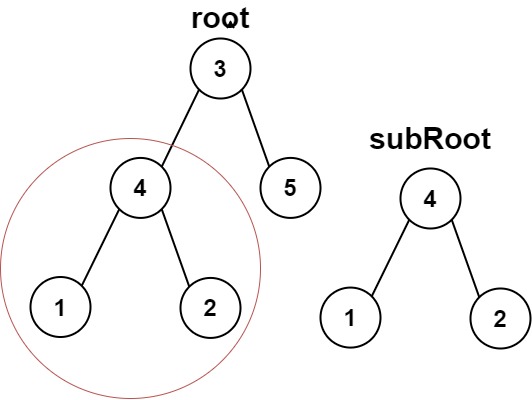
輸入：root = [3,4,5,1,2], subRoot = [4,1,2]
輸出：true

示例 2：

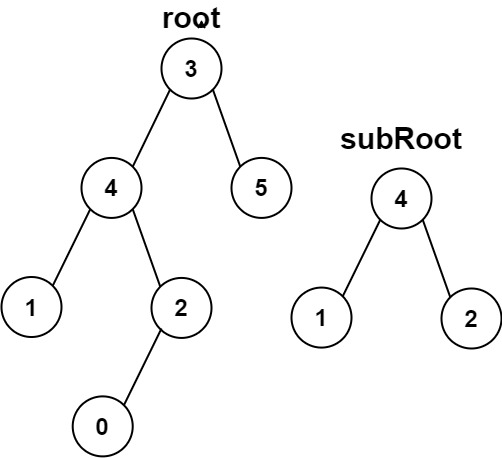
輸入：root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
輸出：false

這道題是相同的樹那道題的變形題，求一個樹的子樹是否包含了另一個樹，也就是可以將這個樹的所有子樹與另一個樹做比較即可，判斷所有子樹中是否存在另一棵樹

所以下面的代碼可以先引入兩棵樹是否相同的代碼，進行復用，最終的返回值在左右子樹間?|| ，因為只要左右子樹有一個子樹包含了subRoot，就符合題意，所以選邏輯或(||) 而不是邏輯與(&&)

代碼如下：

class Solution {
public:  //判斷兩個樹是否相同bool isSameTree(TreeNode* p, TreeNode* q){if(p == nullptr && q == nullptr)return true;if(p == nullptr || q == nullptr)return false;if(p->val != q->val)return false;return isSameTree(p->left, q->left)&& isSameTree(p->right, q->right);}bool isSubtree(TreeNode* root, TreeNode* subRoot) {if(root == nullptr) return false;//前序遍歷，每次先將root與subRoot傳入，比較是否相同if(isSameTree(root, subRoot))return true;//如果不同，就將root的左右子樹與subRoot做比較return isSubtree(root->left, subRoot)|| isSubtree(root->right, subRoot);}
};

題目六：二叉樹的前序遍歷

給你二叉樹的根節點?root?，返回它節點值的?前序?遍歷。

示例 1：

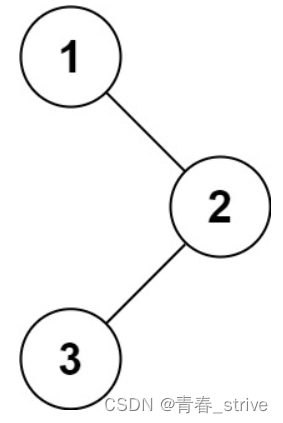
輸入：root = [1,null,2,3]
輸出：[1,2,3]

這道題非常簡單，是一個經典的前序遍歷，要求就是將遍歷后的結點的val值存入vector中

代碼如下：

class Solution 
{
public:void preorder(TreeNode* root, vector<int>& v){if(root == nullptr) return;v.push_back(root->val);preorder(root->left, v);preorder(root->right, v);}vector<int> preorderTraversal(TreeNode* root) {vector<int> v;//preorder用于進行先序遍歷preorder(root, v);return v;}
};

類似的中序，后序就不寫了，與前序相比只是交換了一下順序?

題目七：二叉樹遍歷

編一個程序，讀入用戶輸入的一串先序遍歷字符串，根據此字符串建立一個二叉樹（以指針方式存儲）。例如如下的先序遍歷字符串： ABC##DE#G##F### 其中“#”表示的是空格，空格字符代表空樹。建立起此二叉樹以后，再對二叉樹進行中序遍歷，輸出遍歷結果。

輸入描述：

輸入包括1行字符串，長度不超過100。

輸出描述：

可能有多組測試數據，對于每組數據，輸出將輸入字符串建立二叉樹后中序遍歷的序列，每個字符后面都有一個空格。每個輸出結果占一行。

前面做的題都是接口型，這道題是IO型，也就是要我們書寫所有的代碼，包括輸入輸出

這道題需要先創建一個二叉樹的結構體，包含val和左右指針

再根據給出的先序遍歷的字符串，得到一個二叉樹，其中 # 表示空格

再將得到的二叉樹進行中序遍歷打印出來

代碼如下：

#include <iostream>
#include <string>
using namespace std;
//構建一個樹
struct Tree
{char val;Tree* left;Tree* right;Tree(char c):val(c), left(nullptr), right(nullptr){}
};
//中序遍歷
void order(Tree* root)
{if(root == nullptr) return;order(root->left);cout << root->val << " ";order(root->right);
}Tree* CreateTree(char* str, int& i)
{if(str[i] == '#'){i++;return nullptr;}//每次如果不是 # 就new一個結點Tree* root = new Tree(str[i++]);//接著進入root的左右字樹root->left = CreateTree(str, i);root->right = CreateTree(str, i);return root;
}int main() 
{char s[100];cin >> s;int i = 0;//根據前序的字符串獲得一個二叉樹Tree* root = CreateTree(s, i);//打印中序遍歷的值order(root);return 0;
}

題目八：根據二叉樹創建字符串

給你二叉樹的根節點?root?，請你采用前序遍歷的方式，將二叉樹轉化為一個由括號和整數組成的字符串，返回構造出的字符串。

空節點使用一對空括號對?"()"?表示，轉化后需要省略所有不影響字符串與原始二叉樹之間的一對一映射關系的空括號對。

示例 1：

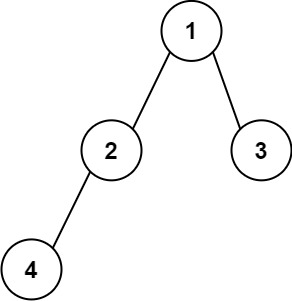
輸入：root = [1,2,3,4]
輸出："1(2(4))(3)"
解釋：初步轉化后得到 "1(2(4)())(3()())" ，但省略所有不必要的空括號對后，字符串應該是"1(2(4))(3)" 。

示例 2：

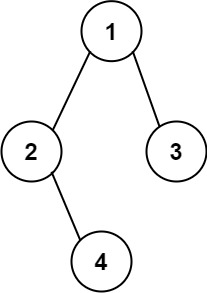
輸入：root = [1,2,3,null,4]
輸出："1(2()(4))(3)"
解釋：和第一個示例類似，但是無法省略第一個空括號對，否則會破壞輸入與輸出一一映射的關系。

題目要求：一個結點的左右孩子需要在該結點右邊帶括號，按照示例一來說明題意：

先是1()()
1有左孩子2右孩子3，所以是：1(2)(3)
2有左孩子4右孩子為空，所以是:1(2(4)())(3)
3左右孩子都為空，所以是：1(2(4)())(3()())

省略括號后，變為了1(2(4))(3)，需要注意的是，這里的省略括號，如果右孩子存在，左孩子不存在是不能省略的，因為此時分不清是左孩子還是右孩子了，詳情見示例二

根據上面的樣例，可以明白有這樣幾種情況：
①左右都不為空，則都不省略括號
②左右都為空，都省略括號
③左不為空，右為空，可以省略右括號
④左為空，右不為空，不能省略左括號
總結就是：如果右不為空，無論左邊是否為空，右邊都需要加括號
? ? ? ? ? ? ? ? ? 如果左不為空或右不為空，則左邊需要加括號

代碼如下：

class Solution {
public:string tree2str(TreeNode* root) {//若root為空，則返回一個string的匿名對象if(root == nullptr){return string();}//括號省略的情況//左右都不為空則都不省略//左右都為空，都省略//左不為空，右為空，省略//左為空，右不為空，不省略//總結就是，如果右不為空，右邊需要加括號//         如果左不為空或右不為空，左邊需要加括號string str;//to_string將val轉換為字符變量，以便可以+=str += to_string(root->val);if(root->left || root->right){str += '(';str += tree2str(root->left);str += ')';}if(root->right){str += '(';str += tree2str(root->right);str += ')';}return str;}
};

題目九：二叉樹的層序遍歷I

給你二叉樹的根節點?root?，返回其節點值的?層序遍歷?。（即逐層地，從左到右訪問所有節點）。

示例 1：

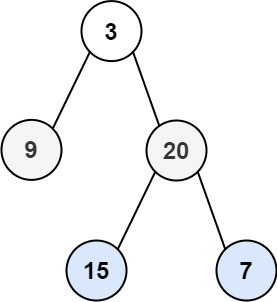
輸入：root = [3,9,20,null,null,15,7]
輸出：[[3],[9,20],[15,7]]

示例 2：

輸入：root = [1]
輸出：[[1]]

示例 3：

輸入：root = []
輸出：[]

這道題二叉樹的層序遍歷，不是簡單直接將每一層打印出來，而是將每一層都保存在一個數組中，存在vector<vector<int>>，然后打印出來

現在的思路就是定義一個變量leveSize，表示每一層的個數，首先root不為空，就將root存進隊列中

循環一層中的結點時，每次都將該結點的val值尾插到一個vector中，再將該結點的左右孩子插入到隊列中，循環完后將vector<int>尾插到vector<vector<int>>中，接著繼續循環

代碼如下：

class Solution 
{
public:vector<vector<int>> levelOrder(TreeNode* root) {queue<TreeNode*> q;int levelSize = 0;if(root){levelSize = 1;q.push(root);}vector<vector<int>> vv;while(!q.empty()){//tmp用于存儲每一層結點的val值vector<int> tmp;//上一層有levelSize個結點，所以循環levelSize次for(int i = 0; i < levelSize; i++){//每次取出一層的一個結點，尾插進tmp中，再pop掉TreeNode* front = q.front();q.pop();tmp.push_back(front->val);//每次都需要判斷該層的這個結點有沒有左右孩子，如果有就插入隊列if(front->left)q.push(front->left);if(front->right)q.push(front->right);}//到這說明某一層的結點循環完了，需要將tmp尾插到vv了vv.push_back(tmp);//更新下一層的levelSize，當前隊列中存的就是上一層結點的左右孩子levelSize = q.size();}return vv;}
};

題目十：二叉樹的層序遍歷II

給你二叉樹的根節點?root?，返回其節點值?自底向上的層序遍歷?。（即按從葉子節點所在層到根節點所在的層，逐層從左向右遍歷）

示例 1：

輸入：root = [3,9,20,null,null,15,7]
輸出：[[15,7],[9,20],[3]]

示例 2：

輸入：root = [1]
輸出：[[1]]

示例 3：

輸入：root = []
輸出：[]

解法一：層序遍歷I + reverse

這道題和上道題幾乎一樣，區別就是這道題要求自底向上的層序遍歷，那么最簡單的方法就是將上一道題的代碼，最終返回的vv，調用算法庫中的reverse即可，就翻轉過來了

代碼如下：

class Solution 
{
public:vector<vector<int>> levelOrderBottom(TreeNode* root) {int levelSize = 0;queue<TreeNode*> q;if(root){levelSize = 1;q.push(root);}vector<vector<int>> vv;while(!q.empty()){vector<int> tmp;while(levelSize--){TreeNode* front = q.front();q.pop();tmp.push_back(front->val);if(front->left)q.push(front->left);if(front->right)q.push(front->right);}vv.push_back(tmp);levelSize = q.size();}//與上一題的代碼一樣，只是下面調用了reversereverse(vv.begin(), vv.end());return vv;}
};

解法二：使用棧來進行倒著輸出層序遍歷

因為棧是后進先出的，所以按層的次序插入以后，出棧就是自底向上的

前面的邏輯和之前一樣，只是在每一層結點遍歷完之后，將vector插入棧中，最后出棧即可

代碼如下：

class Solution 
{
public:vector<vector<int>> levelOrderBottom(TreeNode* root) {int levelSize = 0;queue<TreeNode*> q;if(root){levelSize = 1;q.push(root);}vector<vector<int>> vv;stack<vector<int>> st;while(!q.empty()){vector<int> tmp;while(levelSize--){TreeNode* front = q.front();q.pop();tmp.push_back(front->val);if(front->left)q.push(front->left);if(front->right)q.push(front->right);}st.push(tmp);levelSize = q.size();}//出棧while(!st.empty()){vv.push_back(st.top());st.pop();}return vv;}
};

題目十一：二叉樹的最近公共祖先

給定一個二叉樹, 找到該樹中兩個指定節點的最近公共祖先。

百度百科中最近公共祖先的定義為：“對于有根樹 T 的兩個節點 p、q，最近公共祖先表示為一個節點 x，滿足 x 是 p、q 的祖先且 x 的深度盡可能大（一個節點也可以是它自己的祖先）。”

示例 1：

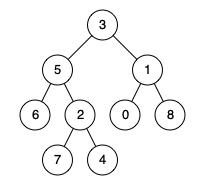
輸入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
輸出：3
解釋：節點 5 和節點 1 的最近公共祖先是節點 3 。

示例 2：

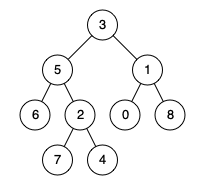
輸入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
輸出：5
解釋：節點 5 和節點 4 的最近公共祖先是節點 5 。因為根據定義最近公共祖先節點可以為節點本身。

示例 3：

輸入：root = [1,2], p = 1, q = 2
輸出：1

這道題需要注意的就是自己也算自己的祖先，并且p/q都在這棵樹中，所以就可以不用判斷p/q是否存在的這種臨界問題

解法一：常規解法，判斷p/q的位置

我們通過觀察這道題的規則，可以發現，如果一個它是左子樹的結點，一個它是右子樹的結點，那么它就是最近公共祖先

如果是三叉鏈，可以找到兩個結點的路徑，轉換為鏈表相交問題，但是此題并不是三叉鏈

所以我們先需要判斷給出的兩個結點p、q在root的左還是右，如果一個在左一個在右，就說明root就是最近公共祖先，如果都在左子樹，就說明公共祖先在左子樹中，反之就在右子樹中

這時會有個特殊情況，如果這兩個結點其中一個是另一個的孩子，那么這個結點就是最近公共祖先

代碼中會寫一個Find函數，用于判斷某一個結點是否在某一個子樹中

代碼如下：

class Solution {
public://Find函數用于尋找x結點是否在sub子樹中bool Find(TreeNode* sub, TreeNode* x){if(sub == nullptr) return false;if(sub == x) return true;return Find(sub->left, x)|| Find(sub->right, x);}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {//這道題不會進入這個語句，因為p/q一定在root中，所以root不可能是空//只是為了嚴謹寫了這個語句if(root == nullptr)return nullptr;//p/q其中一個是另一個的孩子，直接返回if(root == p || root == q)return root;//定義四個指針，表示p/q在root的左子樹還是右子樹bool pInLeft, pInRight, qInLeft, qInRight;//p/q結點不在root的左就在右，所以可以邏輯取反pInLeft = Find(root->left, p);pInRight = !pInLeft;qInLeft = Find(root->left, q);qInRight = !qInLeft;//如果在root的一左一右，就返回rootif((pInLeft && qInRight) || (qInLeft && pInRight))return root;//如果都在root的左子樹，就遞歸進root的左子樹else if(pInLeft && qInLeft){return lowestCommonAncestor(root->left, p, q);}//如果都在root的右子樹，就遞歸進root的右子樹else if(pInRight && qInRight){return lowestCommonAncestor(root->right, p, q);}//照顧編譯器return nullptr;}   
};

這道題上述解法的時間復雜度是：O(H * N)，H表示樹的高度

如果說題目給了這棵樹是搜索二叉樹，那就不需要進行Find函數來尋找了，直接通過判斷val的大小就能解決，Find的時間復雜度是O(N)

但是題目并沒有給這個條件，那么還能怎么優化呢

解法二：使用棧得到路徑，轉化為相交問題

也就是前序遍歷，分別去找p和q結點，找到后將尋找結點時的結點路徑存在棧中，最終將經過的路徑轉化為相交問題即可

而這里的用棧去解決，也就是先進行前序遍歷，先將該結點放入棧中，然后繼續前序遍歷，直到遍歷到空為止，就說明當前放入棧中結點的左孩子為空，此時就遍歷當前結點的右孩子，如果也為空，那就將當前棧頂的元素pop掉

接著以目前棧頂元素為根，直到找到p和q結點為止，此時棧中存儲的就是p和q的路徑，由于棧后進先出的原則，得到的就是從p和q結點到root的路徑，下面演示該解法的過程：

假設要找的結點是6和4，通過前序遍歷，找到了6和4結點

結點6在棧中存儲的路徑是：6? 5? 3
結點4在棧中存儲的路徑是：4? 2? 5? 3

因為結點4的路徑長，所以先將結點4pop掉一個，變為2? 5? 3

此時判斷兩個棧中棧頂元素是否相同，如果不同就pop，如果相同就找到了最近公共祖先

首先6和2不同，都pop掉，再比較5和5，是相同的，所以直接返回結點5即可

找路徑的時間復雜度是O(N)，尋找棧中的結點的最近公共祖先，時間復雜度也是O(N)，因為并沒有套在一起，所以最終時間復雜度也就是O(N)，相比于上面的那種算法的O(H * N)，得到了很大的改進

代碼如下：

class Solution {
public:bool FindPath(TreeNode* root, TreeNode* x, stack<TreeNode*>& path){//如果當前結點為空，就return falseif(root == nullptr) return false;//先將當前節點插入到棧中path.push(root); //如果找到了當前結點，就return trueif(root == x) return true;//在當前結點的左子樹中找，如果找到就不用去右子樹中找了if(FindPath(root->left, x, path)) return true;//在當前結點的左子樹沒找到，繼續到右子樹中找if(FindPath(root->right, x, path)) return true;//如果當前結點的左右字樹都沒有找到，就將當前的結點pop掉，再return falsepath.pop(); return false;}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {//創建兩個棧，分別保存p和q的路徑結點stack<TreeNode*> pPath, qPath;//在FindPath中分別找p和q的路徑FindPath(root, p, pPath);FindPath(root, q, qPath);//讓長的路徑先走出長出的部分while(pPath.size() != qPath.size()){if(pPath.size() > qPath.size())pPath.pop();elseqPath.pop();}//直到找到兩個路徑的交點，就是最近公共祖先while(pPath.top() != qPath.top()){small.pop();big.pop();}return pPath.top();}
};

題目十二：搜索二叉樹與雙向鏈表

輸入一棵二叉搜索樹，將該二叉搜索樹轉換成一個排序的雙向鏈表。如下圖所示

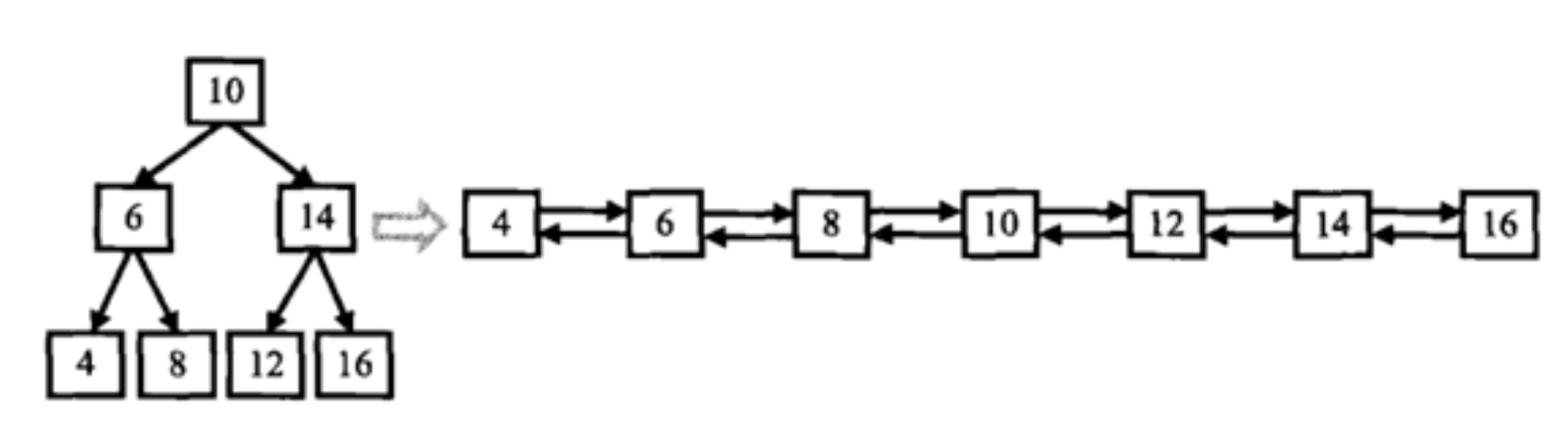
數據范圍：輸入二叉樹的節點數?0 ≤ n ≤ 1000，二叉樹中每個節點的值?0 ≤ val ≤ 1000
要求：空間復雜度O(1)（即在原樹上操作），時間復雜度O(n)

注意:

1.要求不能創建任何新的結點，只能調整樹中結點指針的指向。當轉化完成以后，樹中節點的左指針需要指向前驅，樹中節點的右指針需要指向后繼
2.返回鏈表中的第一個節點的指針
3.函數返回的TreeNode，有左右指針，其實可以看成一個雙向鏈表的數據結構

4.你不用輸出雙向鏈表，程序會根據你的返回值自動打印輸出

輸入描述：

二叉樹的根節點

返回值描述：

雙向鏈表的其中一個頭節點。

這道題看題目的示意圖，就是采用的中序遍歷

所以首先可以解決左指針 left 的問題，采用中序遍歷的思路，先找到最左邊的結點，將其作為cur結點，放在題目所給的圖就是下面的樣子：

此時執行?cur->left =?prev，接著執行 prev = cur，表示改變prev的指向

中序遍歷下一個結點就是6，所以中序遍歷到下一個結點的時候，cur 指向6，再將 cur->left = prev

以此類推，從而完成 left 指針的指向

而 right 指針有兩種方式完成指向：

第一種，采用倒著的中序遍歷，即按照右子樹 -> 根 -> 左子樹的順序，還是按照上面的方式，定義兩個指針，每次遍歷到結點時確定指針的指向即可，這種比較麻煩，所以看第二種方式：

第二種，按照上面指向的邏輯，prev是cur的left，所以同樣的，cur就是prev的right，所以在執行 cur->left = prev時，順便也指定 right 指針的指向，即 prev->right = cur，這里需要注意的就是prev剛開始是空指針，不能指向，所以需要判斷非空再改變指向

最后至關重要的一點：prev指針需要引用傳參

因為我們代碼中執行的中序遍歷是遞歸操作，prev在一層一層返回時，會變為指向調用該層遞歸時的結點，而我們想要的是prev一直是cur的上一個位置，不會因為遞歸結束就改變，所以需要傳入引用調用

代碼如下：

class Solution 
{
public:// 中序遍歷void Inorder(TreeNode* cur, TreeNode*& prev){if(cur == nullptr) return;Inorder(cur->left, prev);// 指定 left 指針cur->left = prev;// 如果prev不為空，指定 right 指針if(prev) prev->right = cur;// prev 指向 cur的位置prev = cur;Inorder(cur->right, prev);}TreeNode* Convert(TreeNode* pRootOfTree) {TreeNode* prev = nullptr;Inorder(pRootOfTree, prev);// 最終需要得到中序遍歷的第一個結點，所以循環找head->left即可TreeNode* head = pRootOfTree;// 因為有可能傳入的head為空，所以while的條件加上headwhile(head && head->left)head = head->left;return head;}
};

題目十三：前序與中序遍歷序列構造二叉樹

給定兩個整數數組?preorder?和?inorder?，其中?preorder?是二叉樹的先序遍歷，?inorder?是同一棵樹的中序遍歷，請構造二叉樹并返回其根節點。

示例 1:

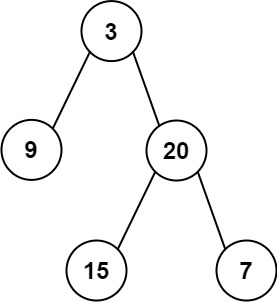
輸入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
輸出: [3,9,20,null,null,15,7]

示例 2:

輸入: preorder = [-1], inorder = [-1]
輸出: [-1]

這道題就是非常經典的給一個前序和中序遍歷的順序，構造一棵樹；或者是給出一個中序和后續遍歷的順序，構造一棵樹，方法是一樣的

但是這種情況必須要有中序，因為前序和后序是確定根結點，而中序能夠確定它的左右字樹

這道題首先需要根據前序遍歷的順序，依次找到當前需要創建的節點，每次找到該節點后需要在中序遍歷中找到該節點，從而得到該節點的左右子樹包含的節點

假設cur就是中序遍歷中找到的當前節點，此時中序遍歷就會分為三部分：
[inbegin, cur - 1] cur [cur + 1, inend]

這三部分的內容，就表示cur節點的和cur節點的左右子樹的節點，所以就根據這三部分，繼續進行遞歸操作，root->left 就指向 [inbegin, cur - 1] 這個區間，root->right 就指向?[cur + 1, inend] 這個區間

退出遞歸的條件就是區間的左端點的下標大于右端點的下標時，就退出遞歸，return nullptr

代碼如下：

class Solution 
{
public://創建_buildTree函數進行遞歸調用//prei是前序遍歷結果的首元素下標，inbegin、inend是中序遍歷結果首尾元素的下標TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder, int& prei, int inbegin, int inend){if(inbegin > inend)return nullptr;//每次遞歸通過前序遍歷結果創建根結點TreeNode* root = new TreeNode(preorder[prei++]);int cur = inbegin;while(cur <= inend){if(inorder[cur] == root->val)break;elsecur++;}// inorder序列 分為三部分// [inbegin, cur - 1] cur [cur + 1, inend]root->left = _buildTree(preorder,inorder,prei,inbegin,cur-1);root->right = _buildTree(preorder,inorder,prei,cur+1,inend);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {//前序遍歷首元素下標為0int prei = 0;//中序遍歷結果首尾元素的下標為0和inorder.size()-1TreeNode* root = _buildTree(preorder,inorder,prei,0,inorder.size()-1);return root;}
};

題目十四：中序與后序遍歷序列構造二叉樹

給定兩個整數數組?inorder?和?postorder?，其中?inorder?是二叉樹的中序遍歷，?postorder?是同一棵樹的后序遍歷，請你構造并返回這顆?二叉樹?。

示例 1:

輸入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
輸出：[3,9,20,null,null,15,7]

示例 2:

輸入：inorder = [-1], postorder = [-1]
輸出：[-1]

中序和后序構造二叉樹，與前面的前序和中序構造二叉樹方法相差不大，只不過前序和中序的遞歸順序是，根，左子樹，右子樹

而后序遍歷是左子樹，右子樹，根，所以反過來就是根，右子樹，左子樹，在遞歸時就需要先確定右子樹，再確定左子樹

代碼如下：

class Solution 
{
public:TreeNode* _buildTree(vector<int>& inorder, vector<int>& postorder, int& posi, int inbegin, int inend){if(inbegin > inend) return nullptr;TreeNode* root = new TreeNode(postorder[posi--]);int cur = inbegin;while(cur <= inend){if(inorder[cur] != root->val) cur++;else break;}// [inbeign, cur - 1] cur [cur + 1, inend]// 先右子樹再左子樹root->right = _buildTree(inorder, postorder, posi, cur + 1, inend);root->left = _buildTree(inorder, postorder, posi, inbegin, cur - 1);return root;}TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {int posi = postorder.size() - 1;return _buildTree(inorder, postorder, posi, 0, inorder.size() - 1);}
};

題目十五：二叉樹的前中后序遍歷（非遞歸實現）

前序題目為例：

給你二叉樹的根節點?root?，返回它節點值的?前序?遍歷。

下面是演示前序遍歷的非遞歸實現，也就是迭代實現

因為遞歸和迭代是可以互相轉換的，所以我們可以將前序遍歷一顆二叉樹理解為：

先訪問左路結點，在訪問左路結點的右子樹

所以就可以借助棧這個數據結構，先將當前的左路結點依次放入棧中，當左路結點尋找完后，將棧中的結點依次出棧，每次出棧都執行上述的先訪問左路結點，在訪問左路結點的右子樹這個操作

所以執行方式與遞歸非常像，只不過是使用的while循環代替遞歸，在遍歷每個結點時都將該節點放入vector中，最后返回即可

while循環的條件是棧不為空，或是cur不為空
棧不為空是為了保證左路結點的右子樹遍歷完，cur不為空是為了當前遍歷的結點不為空

代碼如下：

class Solution 
{
public:vector<int> preorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> v;TreeNode* cur = root;while(cur || !st.empty()){// 左路結點while(cur){v.push_back(cur->val);st.push(cur);cur = cur->left;}// 棧中的結點依次出棧TreeNode* top = st.top();st.pop();// 左路結點的右子樹cur = top->right;}return v;}
};

同樣中序遍歷就只是訪問時機的區別，只需要在取出棧頂元素時再push_back進vector中即可，因為將一個結點從棧中拿出來，就表示該節點的左樹已經訪問完成了，按照中序遍歷的思路，就該訪問根節點了，所以非遞歸實現的中序遍歷的代碼如下，只在標注的地方做以改變：

class Solution 
{
public:vector<int> preorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> v;TreeNode* cur = root;while(cur || !st.empty()){while(cur){st.push(cur);cur = cur->left;}TreeNode* top = st.top();st.pop();// 出棧后再入vectorv.push_back(cur->val);cur = top->right;}return v;}
};

而后序遍歷相比較前序和中序更復雜一些，因為后續的遍歷順序是：左子樹，右子樹，根，需要左子樹和右子樹都遍歷完，才會訪問根結點

而我們上面的邏輯，當取出棧頂元素時，表示訪問完該節點的左子樹，那么怎么判斷該節點的右子樹是否已經訪問了呢

分為兩種情況，第一種，右子樹為空，那么此時就可以直接將該結點push_back進vector中

第二種，右子樹不為空，此時就可以借助prev結點判斷，如果訪問棧頂結點時，上一次訪問的結點是該結點的右孩子，那就說明已經將該節點的右子樹遍歷一遍了，此時就可以直接push_back進vector中
而如果prev不是該節點的右孩子，就循環上述的過程，即執行 cur = top->right 重復

代碼如下：

class Solution 
{
public:vector<int> preorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> v;TreeNode* prev = nullptr;TreeNode* cur = root;while(cur || !st.empty()){while(cur){st.push(cur);cur = cur->left;}// 當左路結點出棧，說明左子樹已經訪問過了TreeNode* top = st.top();// 這兩種情況說明左右字樹都遍歷完了，可以訪問根結點了if(top->right == nullptr || prev == top->right){v.push_back(cur->val);// 訪問根結點時將 top 賦值給 prevprev = top;st.pop();}// 如果沒有訪問該節點的右子樹，則訪問右子樹else{cur = top->right;}}return v;}
};

二叉樹相關的題目到此結束