[線性RNN系列] Mamba: S4史詩級升級

?前言

iclr24終于可以在openreview上看預印本了

這篇（可能是顛覆之作）文風一眼c re組出品；效果實在太驚艷了，實驗相當完善，忍不住寫一篇解讀分享分享。

TL;DR （overview）

Structured State-Space Model (SSM, S4) 是一個線性時不變系統 ( Linear Time Invariance, LTI), 其參數?(Δ,A,B,C)?是static的，與輸入無關，i.e., data independent。 S4雖然在玩具數據集LRA上表現良好，但是在下游任務普遍拉垮。Attention機制的成功arguably可以認為是有data dependent的QKV矩陣來進行交互，這篇的核心思路是讓這些參數data dependent，做出了如下的改動：

B: batch size, L: sentence length, D: input dimension, N: RNN hidden dimension

我們可以看到?B,C?的大小從原來的?(D,N)?變成了?(B,L,N)?，?Δ?的大小由原來的?D?變成了?(B,L,D)?，每個位置的 B,C,Δ?都不相同（之前是在所有位置共享）。

雖然A沒有data dependent, 但是通過state space model的離散化操作之后,?(Aˉ,Bˉ)?會經過outer product 變成?(B,L,N,D)?的data dependent張量，以一種parameter efficient的方式來達到data dependent的目的。

其余主要改動/貢獻如下（技術細節在文末）：

(1) 由于SSM的參數data dependent, 此時失去了LTI的性質，不能像之前的S4一樣通過FFT來訓練了。本文提出了IO-aware的parallel scan（一種memory bounded算子）算法來進行高效訓練，降低整體的讀寫量從而提高wall-time efficiency。上面提到的outer product的參數化方式也對降低整體讀寫量很有幫助（大致思路是?(Aˉ,Bˉ)?在SRAM里面on-the-fly算出來，避免materialization帶來的讀寫開銷）

(2) 如果用一個線性層參數化?Δ:R[B×L×D]→R[B×L×D]需要?D[2] 參數。本文提出了一種low-rank projection的參數化方式，可以通過很小的額外參數量來獲得較大的提升。最后負責token mixing的SSM只需要很少的參數，絕大多數參數都分給channel mixing了。從MetaFormer的視角來看，token mixing相對channel mixing而言不是重要，所以從這個視角出發的話分配很少的參數是極其合理的。

(3) 以往的SSM經常需要一個output gate來達到很好的效果，如Gated SSM，這個結構跟gated MLP很像。所以作者干脆把token mixing和channel mixing合二為一，提出了一個新的極簡風的Mamba block。（Update: 這跟Gated Attention Unit挺像的）

如下圖所示。

實驗部分是最讓人驚喜的：

Chinchilla scaling laws, 訓練長度2048

其中Transformer++指的是帶有Rope和SwiGLU的版本（i.e., LLaMa用的）。可以看到之前聲稱match Transformer performance的model基本上最多也就match一下vanilla transformer的結果 (i.e., 不帶rope，如圖綠線所示）(吐槽：Hyena是真的辣雞）

Mamba在8192訓練長度上也能match Transformer++的結果

下游任務evaluation，Mamba無情刷榜

技術細節

S4簡介

Recommended Reading:
Structured State Spaces for Sequence Modeling (S4)
Simplifying S4

S4的連續微分方程形式（一般也用不著）：

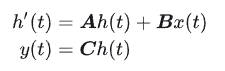
離散形式：

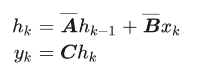
其中最常用到的離散化方法是zero-order hold (ZOH):

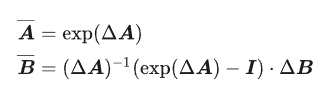
其中?Aˉ∈R[N×N]，Bˉ∈R[N×1]，C∈R[1×N]，Δ∈R，?N?是SSM hidden state的大小。需要強調的是 S4用的是Single-input-single-output (SISO), 即對應于每一個輸入的維度，都有一套獨立的SSM參數（傳統的RNN是MIMO, multiple-input-multiple-output, 很容易混淆）

Parameter-efficient的data dependent參數化方式

上面的S4的參數都是靜態的，這肯定不行（）所以要弄成data dependent的動態的

這一套的思路由來已久，CV領域的dynamic convolutional，Transformers里面的QKV, LSTM里面的gating都是類似的思想

注意到，對于每個input dimension A只需要N個參數, 因為我們通常會對A做對角化

作者用

來將?B,C,Δ?data dependent化，其中??Linear d(X)?是把 D維的輸入向量?X 經過一個線性層map到?d 維。這里的總參數量大概是?D?N?2+D?D?。?N?即SSM的hidden dimension，一般設的比較小 (e.g., 16)，所以?D?N?2?部分的參數量是少頭，而參數化?sΔ?的?D?D?是大頭（一般至少都是幾k維）

所以作者用了一個low-rank projection來降低參數量：

sΔ(X)=LinearD?(Linear1?(X))

這樣總參數量就從?D?D?降低到了?2D?。

最后作者選擇把A設成了data independent，作者給出的解釋是反正離散化之后 Aˉ=exp?(ΔA)?，?Δ?的data dependent能夠讓整體的?Aˉ?data dependent。

（PS: 這個解釋理由感覺有點牽強，因為如果這樣的話，?B?也完全可以data independent，靠?Δ?讓?Bˉ?data dependent)

理解參數的含義和功能

step size?Δthat represents the resolution of the input
discretization of SSMs is the principled foundation of heuristic gating mechanisms.

這個量跟RNN里的gating有著深刻的聯系[1]?，data dependent的?Δ?跟RNN的forget gate的功能類似

經典的RNN gating可以理解成SSM離散化的一個特例。

而 B和C 所起到的功能類似于寫（進RNN的memory）和讀（取RNN的memory）。所以data dependent的B/C的功能跟RNN的input/output gate類似。

A的作用其實有點尷尬，因為?Δ?已經有點遺忘門的意思了。但注意到對于每個input維度來說，?Δ?只是一個標量，而?A∈R[N×1] ，也就是說對應這個維度的SSM來說，A在每個hidden state維度上的作用可以不相同，起到multi-scale/fine-grained gating的作用，這也是LSTM網絡里面用element-wise product的原因（i.e., forget gate是跟隱藏層維度相同的一個向量，而不僅僅是一個標量）

這篇文章所強調的selectivity無非就是傳統門控RNN經典的思想。。。屬于是文藝復興/新瓶裝舊酒
Recommended Reading:
十分推薦一篇鞭辟入里的文章
Written Memories: Understanding, Deriving and Extending the LSTM

IO-aware Parallel Scan

因為現在的參數都是data dependent了，所以不再是LTI，也就失去了卷積的性質，不能用FFT來進行高效訓練了。

不過這也不是什么問題，之前的S5已經指出了data dependent的SSM可以用parallel scan來進行訓練。不過parallel scan依然是memory bounded的操作，對于SSM這種每個input維度對應一個RNN的SISO模型來說，總共有效的RNN hidden state可以理解成?N?D?，所以實現的不好的話很容易比較慢。S5為了避免這個問題，選擇了MIMO的方式并且降低總體的維度。Mamba選擇迎難而上，利用kernel fusion, recomputation的經典優化思想來硬上（PS: 很好很c re組）

一般的實現會提前先把大小為?(B,L,D,N)?的?Aˉ,Bˉ?先算出來，然后把它們從HBM (high-bandwith memory, or GPU memopry) 讀到SRAM, 然后調用scan算子算出?(B,L,D,N)?的output，寫到HBM里面。再開一個kernel把?(B,L,D,N)?的output以及 (B,L,N)?的C讀進來，multiply and sum with C得到最后的?(B,L,N)?output 。整個過程的讀寫是?O(BLDN)?。本文提出的方法：

把?(Δ,A,B,C)?讀到SRAM里面，總共大小是?O(SLN+DN)
在SRAM里面做離散化，得到?(B,L,D,N)?的?Aˉ,Bˉ
在SRAM里面做scan，得到?(B,L,D,N) 的 output
multiply and sum with C，得到最后的 (B,L,D)?output 寫入HBM

整個過程的總讀寫量是?O(BLN)?，比之前省了O(N)。 backward的時候就把?Aˉ,Bˉ?重算一遍，類似于flashattn重算attention分數矩陣的思想。只要重算的時間比讀?O(BLDN)?快就算勝利

We benchmark the speed of the SSM scan operation (N = 16), as well as the end-to-end inference throughput of Mamba, in Figure 8.? Our efficient SSM scan is faster than the best attention implementation that we know of (FlashAttention-2 (Dao, 2023)) beyond sequence length 2K, and up to 20-40× faster than a standard scan implementation in PyTorch.

IO-aware的實現比naive實現快很多倍；(flash)scan 在輸入長度2k的時候就開始比flashattention快了, 之后越長越快。同時scan也比long convolution (w/ FFT)快，再次給long convolution模型敲上喪鐘（本來long conv模型inference的時候就很笨了，訓練還慢就更...

Token mixing+Channel Mixing合二為一

之前的SSM模型要work，都會加上output gating，之后再過個線性層channel mixing，如上圖的最左邊所示。這兩個部分跟Gated MLP（上圖中間）右邊的支路和最上面的channel mixing是一樣的。所以SSM層如果跟Gated MLP疊的話，難免會感覺有點冗余，所以作者干脆把兩個合二為一，把token mixing層和channel mixing層合二為一 (PS: 估計會有很深遠的影響），并且做work了。

現在的新的Mamba block有?3ED[2] 個參數（E是FFN擴展的倍數，一般transformer里面E是擴大四倍）。如果E=4，那么正好對應于一個?12D[2]?也就是一層transformer layer的總參數量。但可能是因為RNN比較吃層數（也很好形象理解，RNN是比較local的模型，所以需要疊深度來換一層attend到的廣度），所以作者選擇E=2，一層包含兩個這樣的Mamda block。

消融實驗

對不同參數data dependent的敏感性

上文提到?Δ?的作用類似遺忘門，而遺忘門毫無疑問是LSTM里面最重要的門[2]，所以這個消融實驗結果發現?Δ?data dependent帶來的收益效果最大就一點都令人驚訝啦

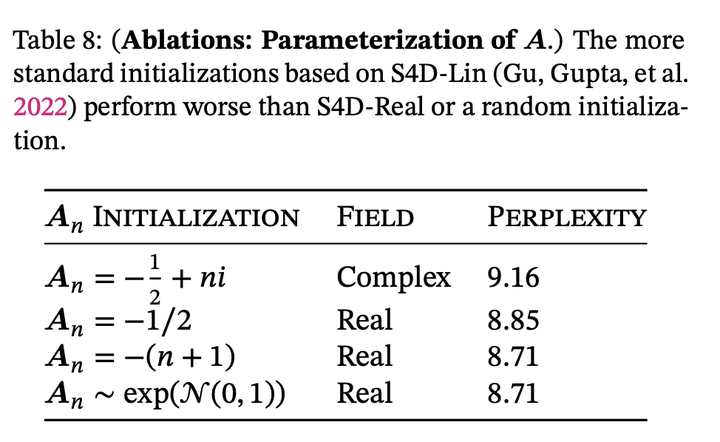
A用實數還是虛數，以及A的參數化方式

這篇發現complex的decay rate不如real；跟rwkv作者的觀點一致。之前的data independent的ssm模型發現虛數挺重要的；這里的實驗現象相左的可能原因是因為data dependent的ssm表達能力本身就足夠強了，不需要復數帶來的額外表達能力；而之前data independent的ssm如果不用虛數來對角化A，表達能力相當受限

\Delta參數化時使用的low-rank的rank size

之前提到了參數化?Δ?的時候用low-rank來降低ssm部分的參數。其中一個可能的深意是 Metaformer框架認為token mixing遠不如channel mixing重要，所以與其把參數分配給token mixing，不如把參數分配給channel mixing。最上面的那一行是data independent；rank=1的時候可以發現就已經有提升了,證明了data dependent的有效性；之后接著加參數也有提升 (但不確定如果多出來的參數加到channel mixing里面會不會更好)