【CTF-Crypto】數論基礎-02
文章目錄
- 【CTF-Crypto】數論基礎-02
- 1-16 二次剩余
- 1-20 模p下-1的平方根*
- 1-21 Legendre符號*
- 1-22 Jacobi符號*
- 2-1 群*
- 2-2 群的性質
- 2-3 阿貝爾群*
- 2-4 子群
- 2-11 群同態
- 2-18 原根
- 2-21 什么是環
- 2-23 什么是域
- 2-25 子環
- 2-26 理想
- 2-32 多項式環
1-16 二次剩余
是什么?

定義:

判斷是否有解的一個方法:把小于模數的全代入一遍,看看有沒有解
如:
把x從1到6分別代入x,會發現方程都不成立
所以3不是模7下的二次剩余
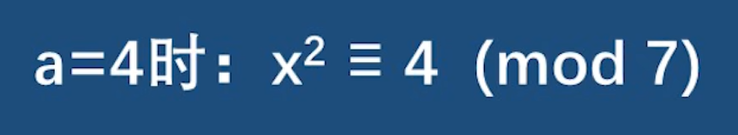
當a=4時, x從1到6嘗試 可以發現2或5可以滿足式子,所以4是模7下的二次剩余
下面進行正向推測,x從1到6 計算右邊

所得結果有1、2、4 表明模7下二次剩余的是a = 1 2 4
問題一般化:模n下,什么樣的整數a才是二次剩余(有平方根)?
首先明確一個二次剩余的集合

這個集合里面的元素就是模n下余數的平方 再模n的結果
故有 該集合里的任意整數a 必然存在整數b 使得b的平方和a模n下同余

從而得到二次剩余的判斷方法

性質
二次剩余的性質和模數有非常密切的關系:
- 模p下的二次剩余
p是奇素數(p是素數,且p不等于2)
回顧:
這個例子剛講過,模7下的二次剩余的a是1 2 4 一共三個 二次非剩余也是3個
同時關于平方根,也可以發現,1對應的平方根是1和6 4對應的平方根是2和5 2對應的平方根是3和4 每個對應的都是兩個
以1為例,看他的兩個平方根分別是1和6 因為是模7 所以6可以寫成-1 因為-1+7 = 6
基于上面這個正負1的情況,在普通運算下沒有任何問題,但是在模運算下需要推導證明

證明:

進而證明下面那個b和c的結論

這個結論告訴我們,如果a=b^2 則a恰有兩個根 正負b
進一步推導,Zp星里的每個整數都可以做平方 其個數就是二次剩余的個數

這個上面也提到過,每個整數對應正負兩個 其中負的那個可以轉化一下
所以真正的個數是我們每次遍歷的一半 也就是p-1的一半
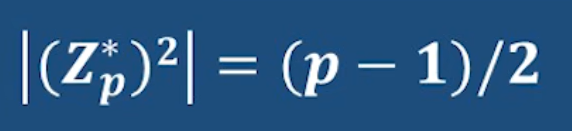
小重點:歐拉準則(二次剩余的判定定理)

第一條證明: 注意下面的式子 都是在模p下 才有等于1的這個結論

具體等于1還是-1 取決于第2條還是第3條 如果是二次剩余 就是1 如果是二次非剩余 就是-1
原因:
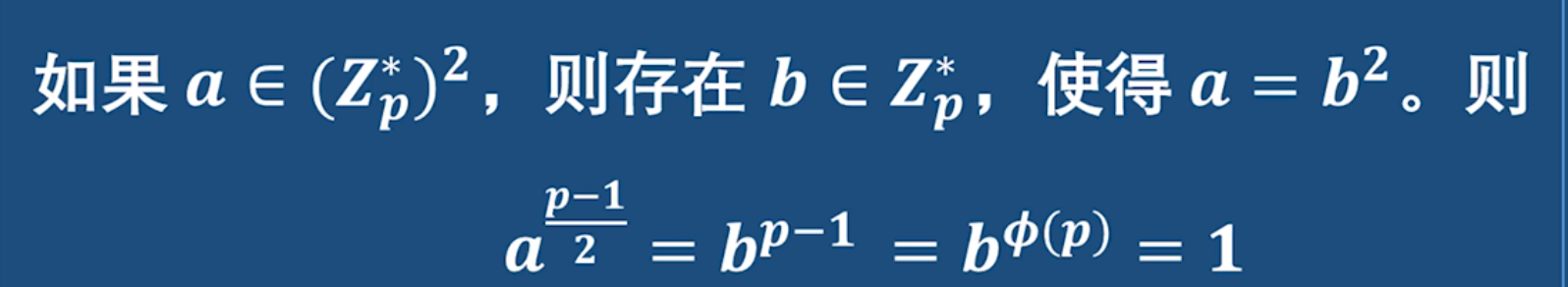
討論兩個整數在模p下相乘 所得積的情況
-
兩個都相同類型的情況下 相乘結果一定是二次剩余

-
如果只有一個整數是二次非剩余 則結果是二次非剩余
計算方法:
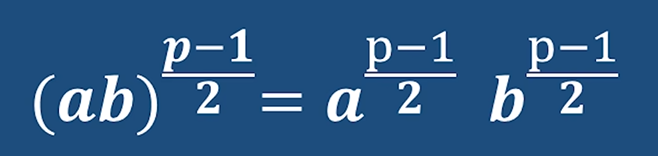
拆開 分別計算 套用歐拉準則
陷阱:如果告訴你兩個數乘積是二次剩余 那么這兩個數也是二次剩余 是錯誤的 因為有可能都是二次非剩余
常見性質 補充版

1-20 模p下-1的平方根*
- 引言:
下面的性質和余數是1的p有關,p是奇素數

- 如何判斷-1是不是模p下的二次剩余
常規思路:對-1使用歐拉準則 看看結果是否等于1
利用性質的簡單方法:
-

舉例:

p % 13 = 14 % 13 = 1 所以根據性質1 得到-1是集合的自己,即-1是模13下的二次
使用歐拉準則證明一下
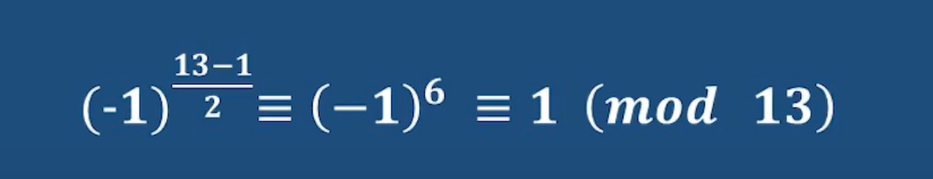
證明:

上面可以看出來 對-1使用歐拉準則所得結果必然是1,此時-1就是二次剩余
?
? 如果是這中情況 模4下和1同余,那么此時-1是二次非剩余
1-21 Legendre符號*
對于奇素數p,在模p下判斷a是否是二次剩余
最直接的方法:
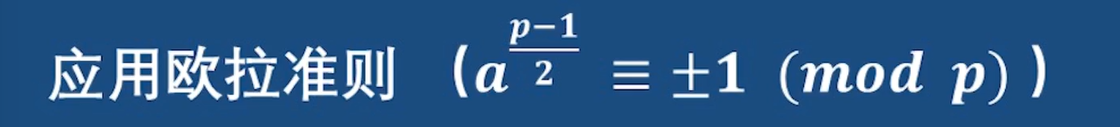
便捷方法:
只要發現p模4和1同余,那么-1就一定是模p下的二次剩余,而不需要對-1使用歐拉準則
但是可以發現上面的這個便捷判斷只能針對-1進行判斷,那么對于其他任意整數呢,如何判斷呢,所以引出了Legendre符號

其中結果為1 表示a是模p的二次剩余
結果為-1 表示a是模p的二次非剩余
但是目前直接看這個好像沒發現什么便捷性,其實利用該符號的一些性質,可以使得運算從指數級運算降低
性質1:歐拉準則和Legendre符號的等價轉換關系
性質2:
證明:利用歐拉準則的形式
應用舉例:
性質3:
因為a和b同余,那么這倆就必然同為二次剩余或同為二次非剩余,必然同時等于1或-1
性質4:
性質5:二次互反律(law of quadratic reciprocity)
特點:
反之為負的
當p等于q時 整除 根據Legendre符號 式子兩邊均為0 等式一定成立
使用方法:
例1:入門:
如果使用歐拉準則
非常麻煩,不好計算
既然7和31都是奇素數,可以應用Legendre符號+二次互反律
首先因為7和31模4都不等于1 所以根據二次互反律符號為負
然后31可以模7化簡一下
剩下的可以試一試 或者 歐拉準則
例2:補充一下上面的應用事項
因為 17 和 31 均為奇素數,所以可以使用二次互反定律 此外因為 17 和 31 模 4 均不為一,所以根據 L e g e n d r e 符號,結果為 1 ( 17 31 ) = ( 31 17 ) 此時可以發現模數變小了,所以可以優化一下分子,令分子模 17 ( 14 17 ) 此時繼續使用二次互反定律!發現是不行的,因為 14 不是奇素數 所以此時使用 L e g e n d r e 的性質,對其進行拆分 ( 14 17 ) = ( 2 17 ) ( 7 17 ) 看到 2 在分子上使用性質 4 ,得到結果為 1 所以最后只剩下 7 17 可以發現均是奇素數,所以可以使用二次互反定律縮小模數 7 17 = 17 7 = 3 7 繼續,二次互換先判斷是否有模 4 余 1 的奇素數,均沒有則領金加符號 17 7 = 3 7 = ? 7 3 = ? 1 3 = ? 1 \\~~~因為17和31均為奇素數,所以可以使用二次互反定律\\ 此外因為17和31模4均不為一,所以根據Legendre符號,結果為1\\ (\frac {17}{31}) =(\frac {31}{17}) \\ 此時可以發現模數變小了,所以可以優化一下分子,令分子模17\\ (\frac {14} {17})~~此時繼續使用二次互反定律!發現是不行的,因為14不是奇素數\\ 所以此時使用Legendre的性質,對其進行拆分(\frac {14} {17})=(\frac{2}{17})(\frac{7}{17})\\ 看到2在分子上 使用性質4,得到結果為1 所以最后只剩下\frac {7}{17}\\ 可以發現均是奇素數,所以可以使用二次互反定律 縮小模數\\ \frac {7}{17} = \frac {17}{7} = \frac{3}{7} \\ 繼續,二次互換 先判斷是否有模4余1的奇素數,均沒有 則領金 加符號 \frac {17}{7} = \frac{3}{7} =-\frac{7}{3}= -\frac{1}{3} = -1 ???因為17和31均為奇素數,所以可以使用二次互反定律此外因為17和31模4均不為一,所以根據Legendre符號,結果為1(3117?)=(1731?)此時可以發現模數變小了,所以可以優化一下分子,令分子模17(1714?)??此時繼續使用二次互反定律!發現是不行的,因為14不是奇素數所以此時使用Legendre的性質,對其進行拆分(1714?)=(172?)(177?)看到2在分子上使用性質4,得到結果為1所以最后只剩下177?可以發現均是奇素數,所以可以使用二次互反定律縮小模數177?=717?=73?繼續,二次互換先判斷是否有模4余1的奇素數,均沒有則領金加符號717?=73?=?37?=?31?=?1
1-22 Jacobi符號*
其實不要把這個符號想的太陌生,其實就是Legendre符號的推廣演化而來

可以發現對分子分母的條件減少了一些限定
注意奇素數p可以彼此相同,這樣右邊的式子就是Legendre符號

當a和n不互素時 結果為0
一些性質 非常類似:

性質5:如果模數是合數,則可以把合數拆分 然后分別計算
? 作用:可以直接把一些大模數化成一些小模數,而且不用關心負號問題
二次互反律的推廣


雅可比符號判斷二次剩余性



第三個表示 如果a是模n下的二次剩余,則雅可比符號為1
推導:
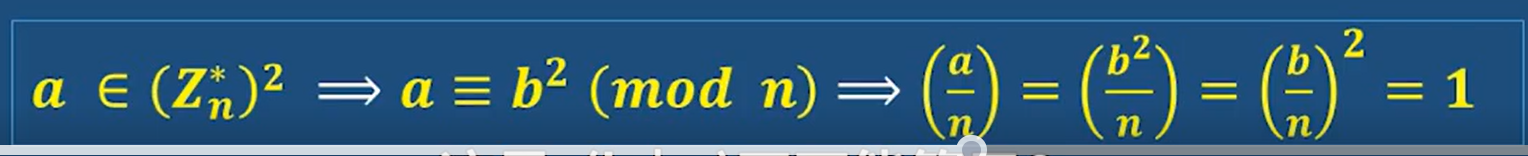
2-1 群*
體系:
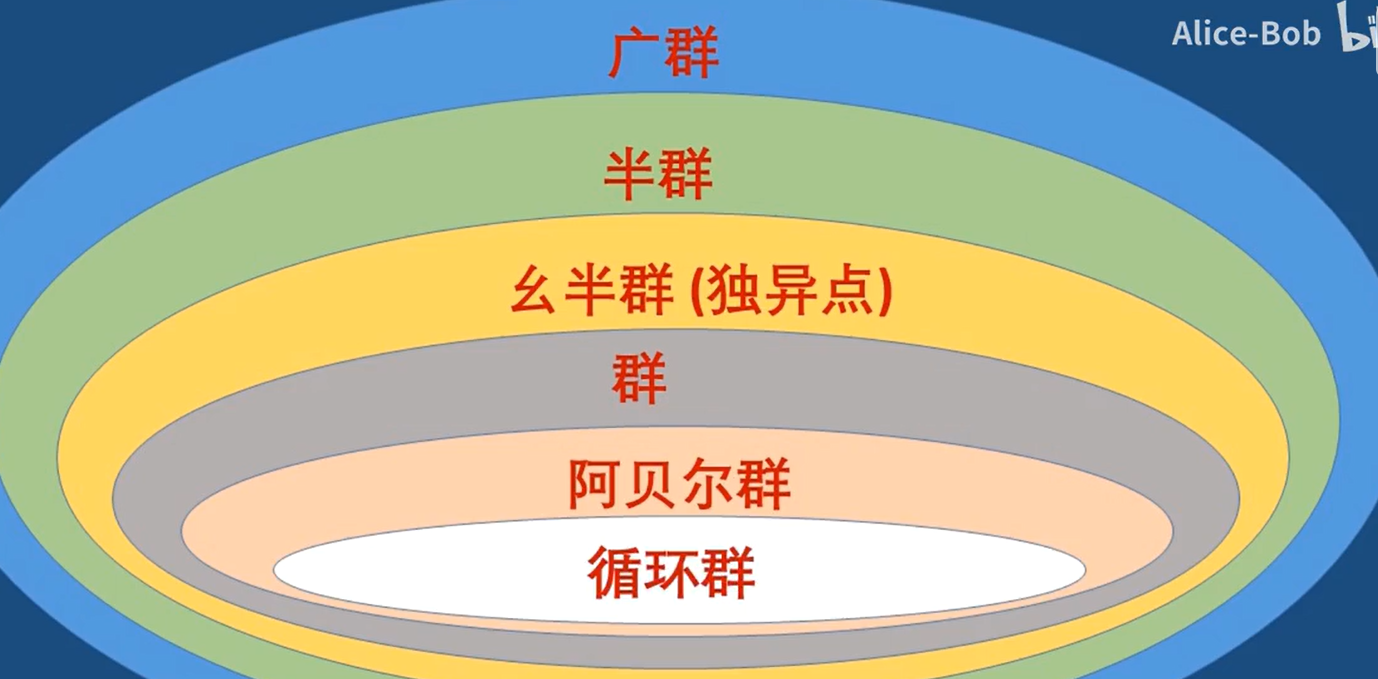
代數結構
- 封閉性
集合里任意兩個元素的二元運算的結果,是跑不出這個集合的
反例

這樣就不能說自己是代數結構
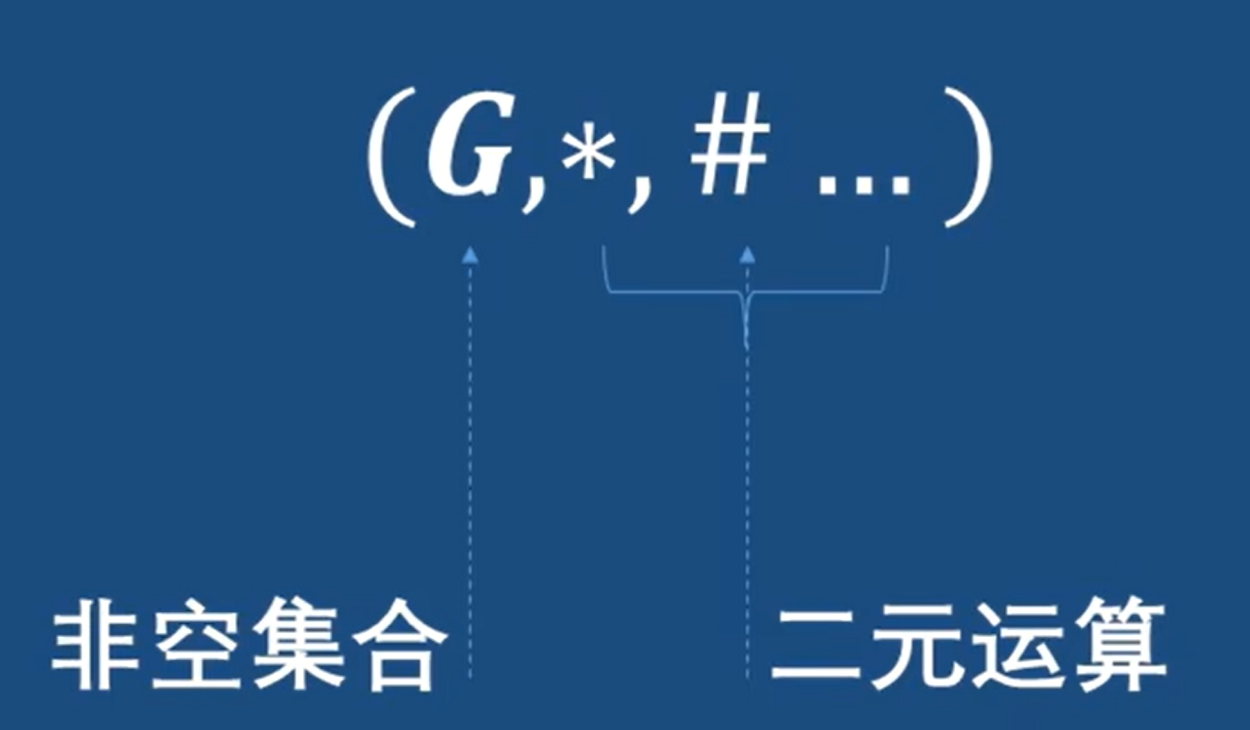
關于群(group)需要滿足下面四個性質:

在一個群中,因為逆元的存在,出現了逆運算
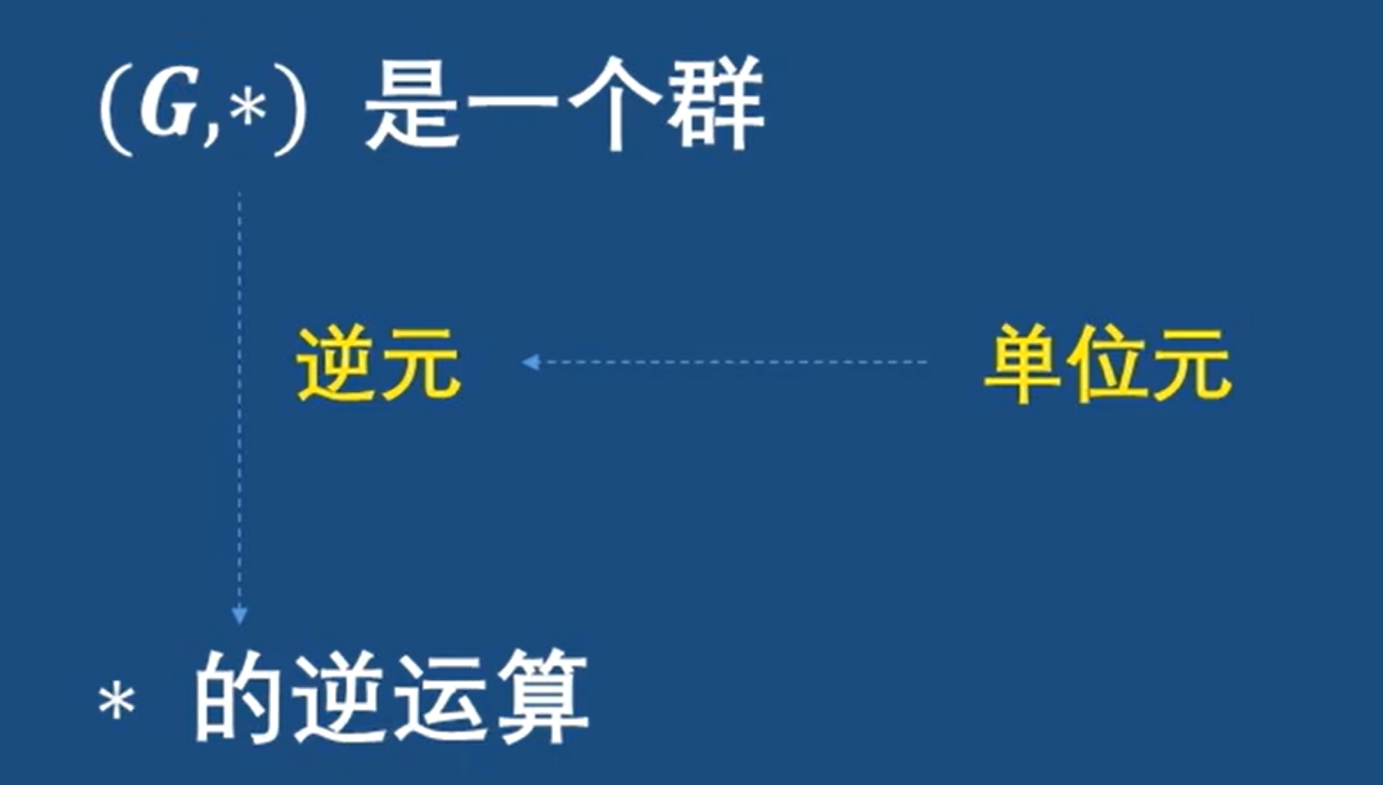
判斷是不是群,就看是否滿足上面四個性質
舉例:
-

-
不是群,

因為有0的存在 修正

- 模運算的例子

小tip:

2-2 群的性質
-
分類:
- 有限群:

- 無限群:

-
定理1 : 群里的單位元是唯一的

計算過程根據單位元的性質,和單位元的運算還等于本身
- 定理2 : 每個元素只有唯一的逆元

注意啊 可能有些元素以自身為逆元
- 平凡群

- 群的性質:
- 消去律
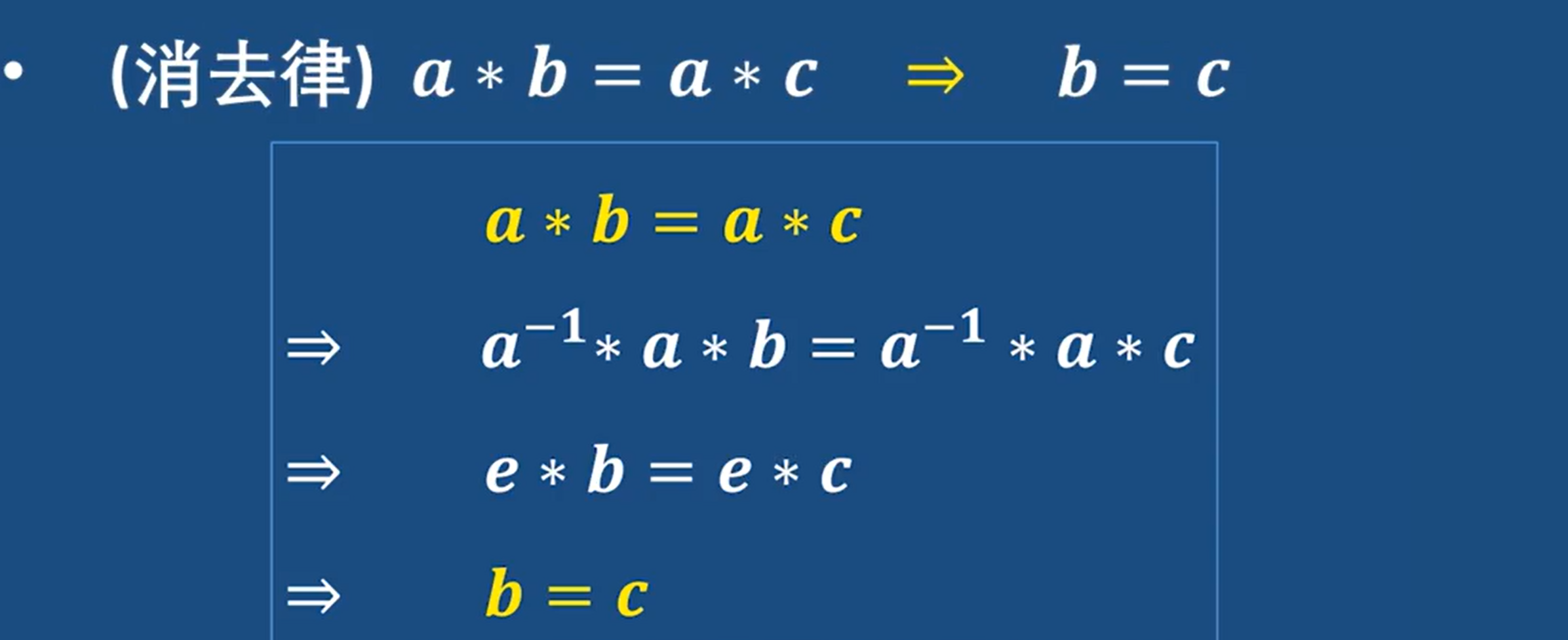
- 方程解

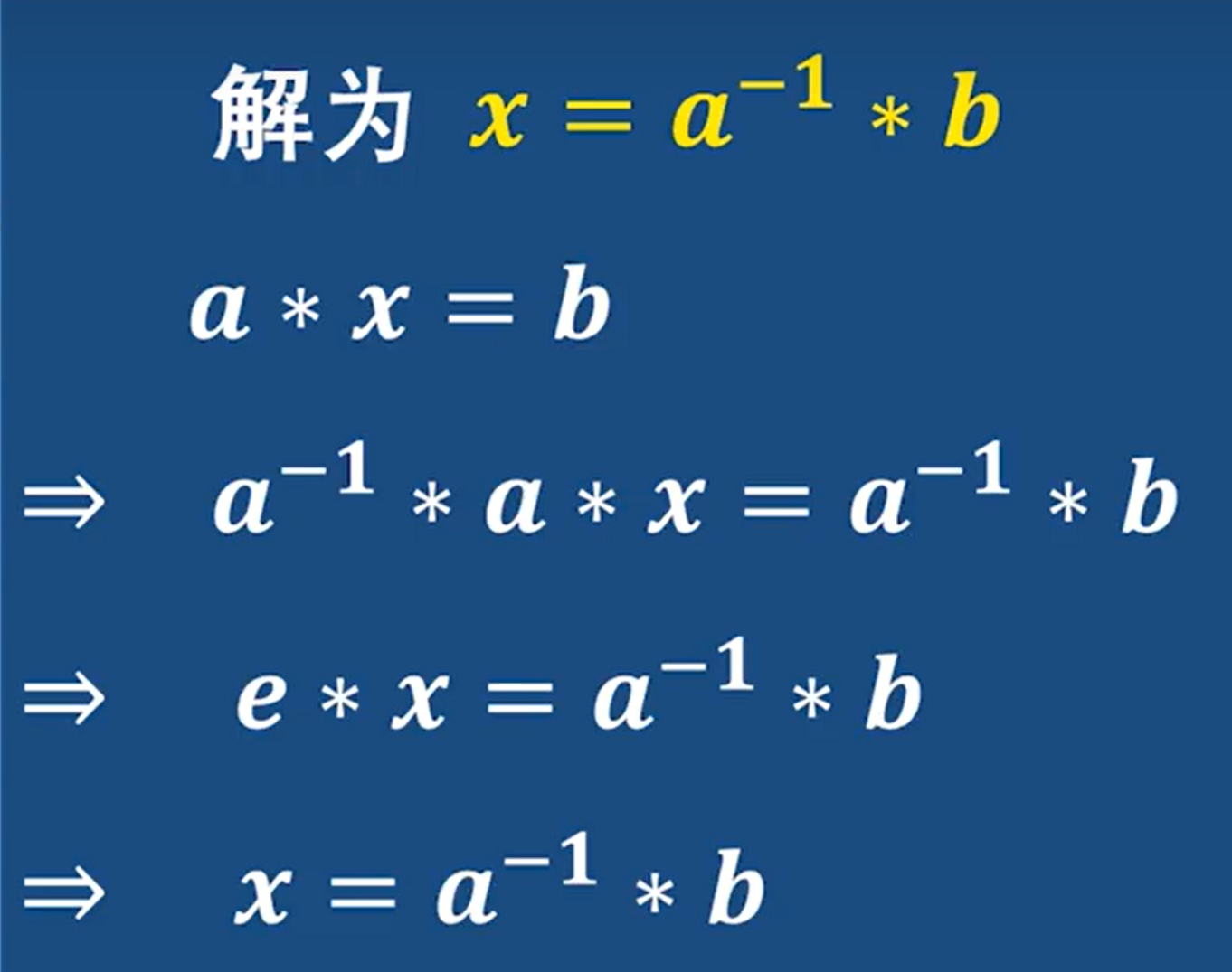
注意:群里的運算不一定滿足交換律 所以左右位置還是有區別的
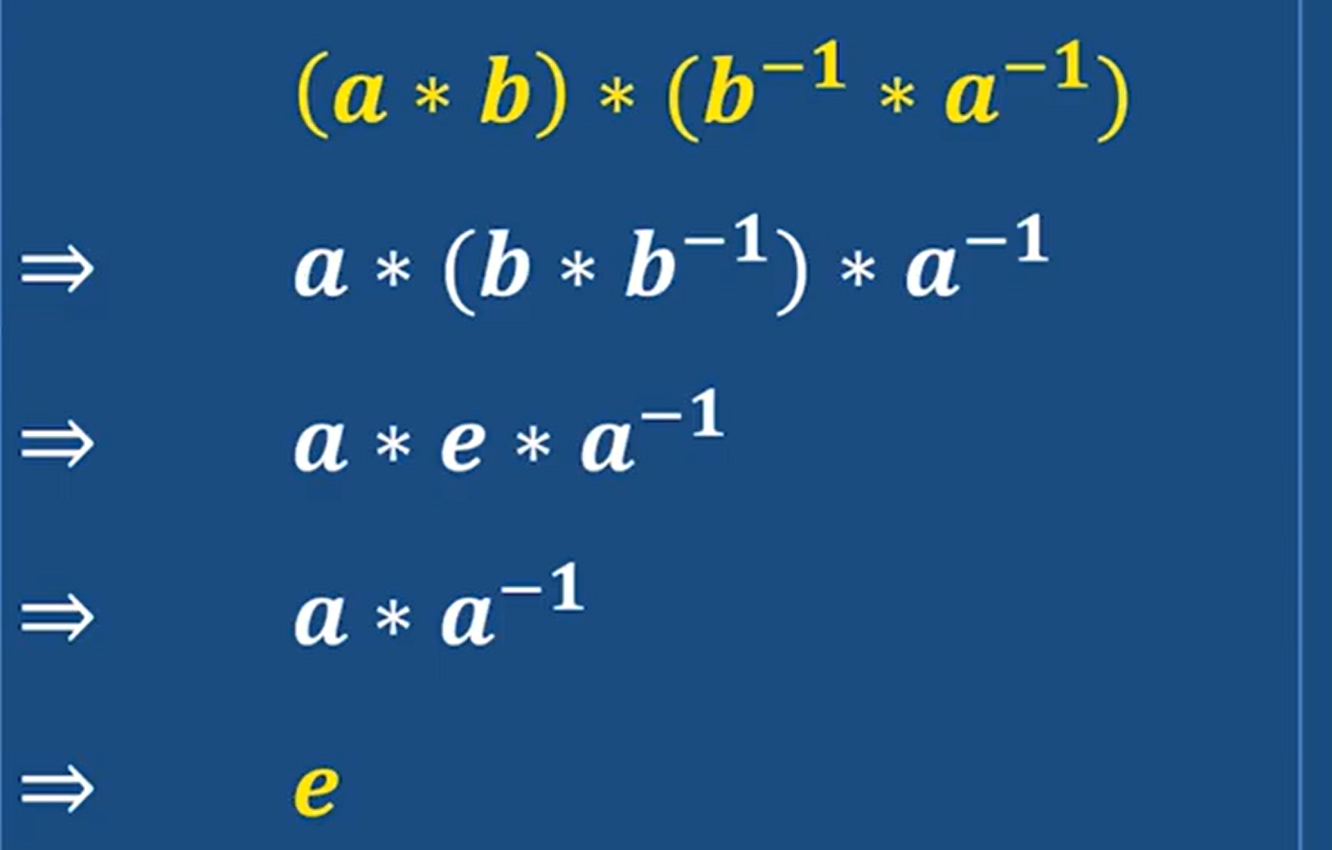
因為a的逆元和a相乘是單位元e 所以a的逆元 和a 互為逆元
2-3 阿貝爾群*
在群的基礎上,多出來一個性質,當運算滿足交換律時,則稱為阿貝爾群,也稱交換群

從群到阿貝爾群,如何快速證明

定理證明:


利用消去律
簡記方法:
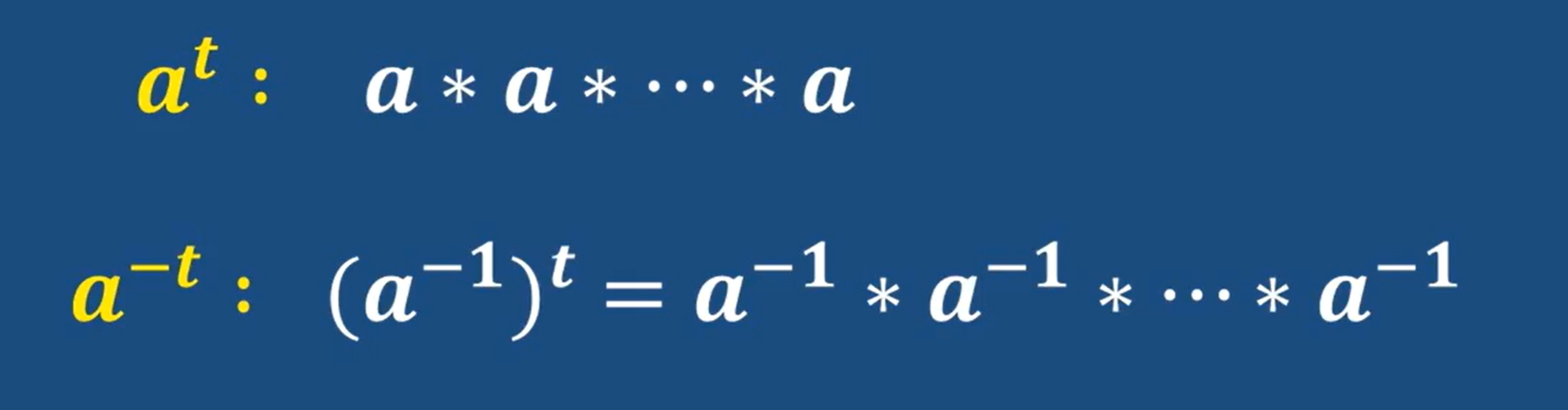
注意這里的次方運算,表示多少個元素做相同運算,符號由群定義,不是單獨的乘方運算
推廣

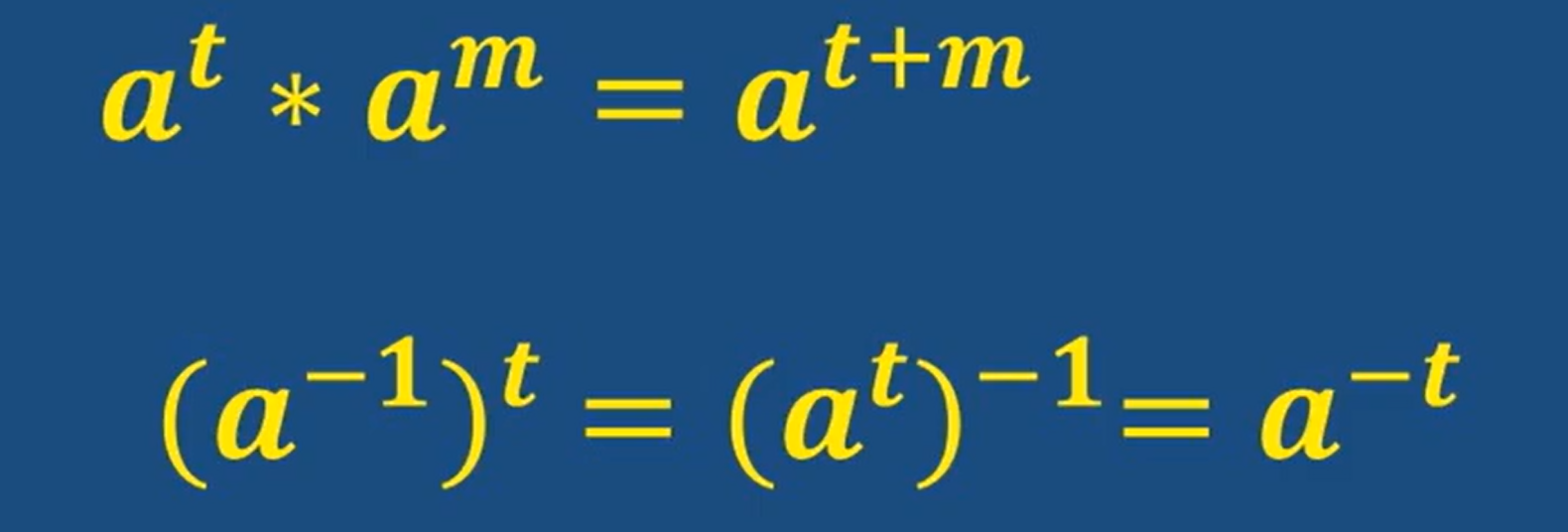
上面這個的證明:證明是逆元關系

來個定理

2-4 子群
定義:

G的子群分類:
-
平凡子群:

-
非平凡子群:

定理:
- 群的單位元也是其子群的單位元

-
元素在子群中,其逆元也必在該子群中

有人問,有沒有可能
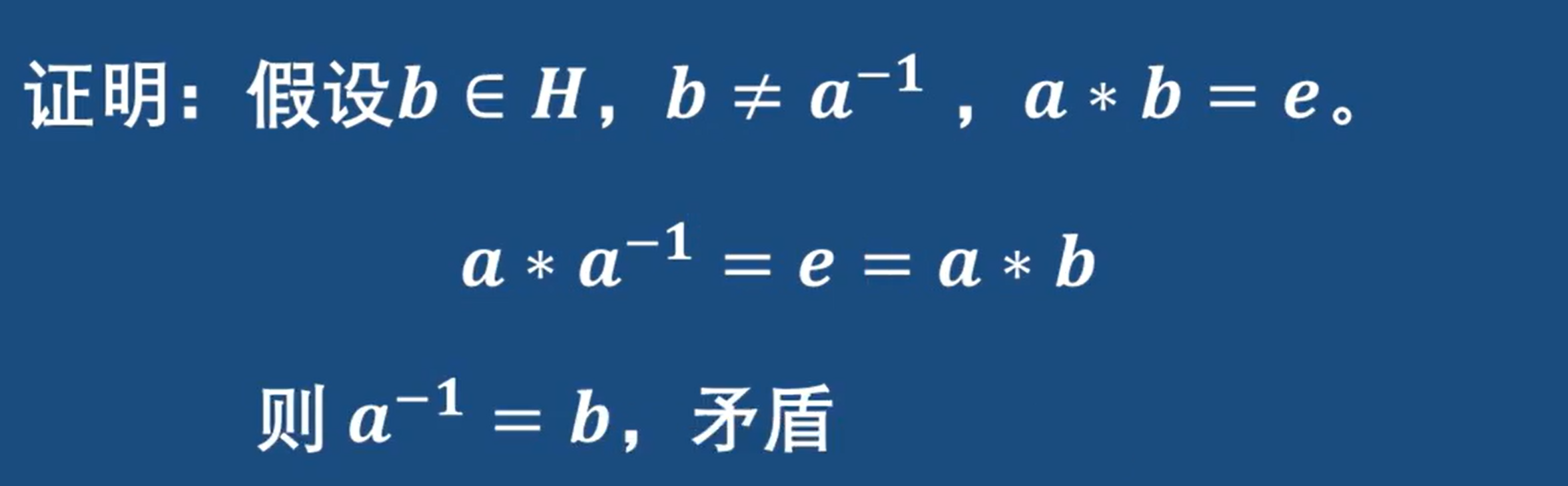
如何判斷子群
方法一:

先證明單位元:式子里a和b可以相等

證明逆元:令a = 單位元e b = a 套用式子

證明封閉性:
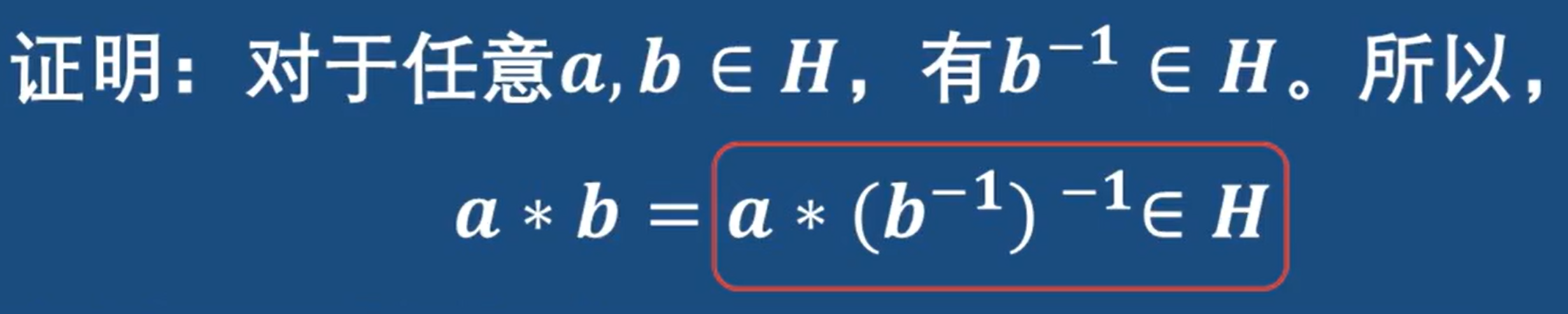
紅框里面在利用式子,b的逆作為式子里的b,得出a和b進行二元運算是屬于H的 結果封閉
結合律:因為G是群 對于其元素 必然滿足結合律
方法2:

2-11 群同態
基本定義

圖示:

兩個特殊子集:
- 同態像
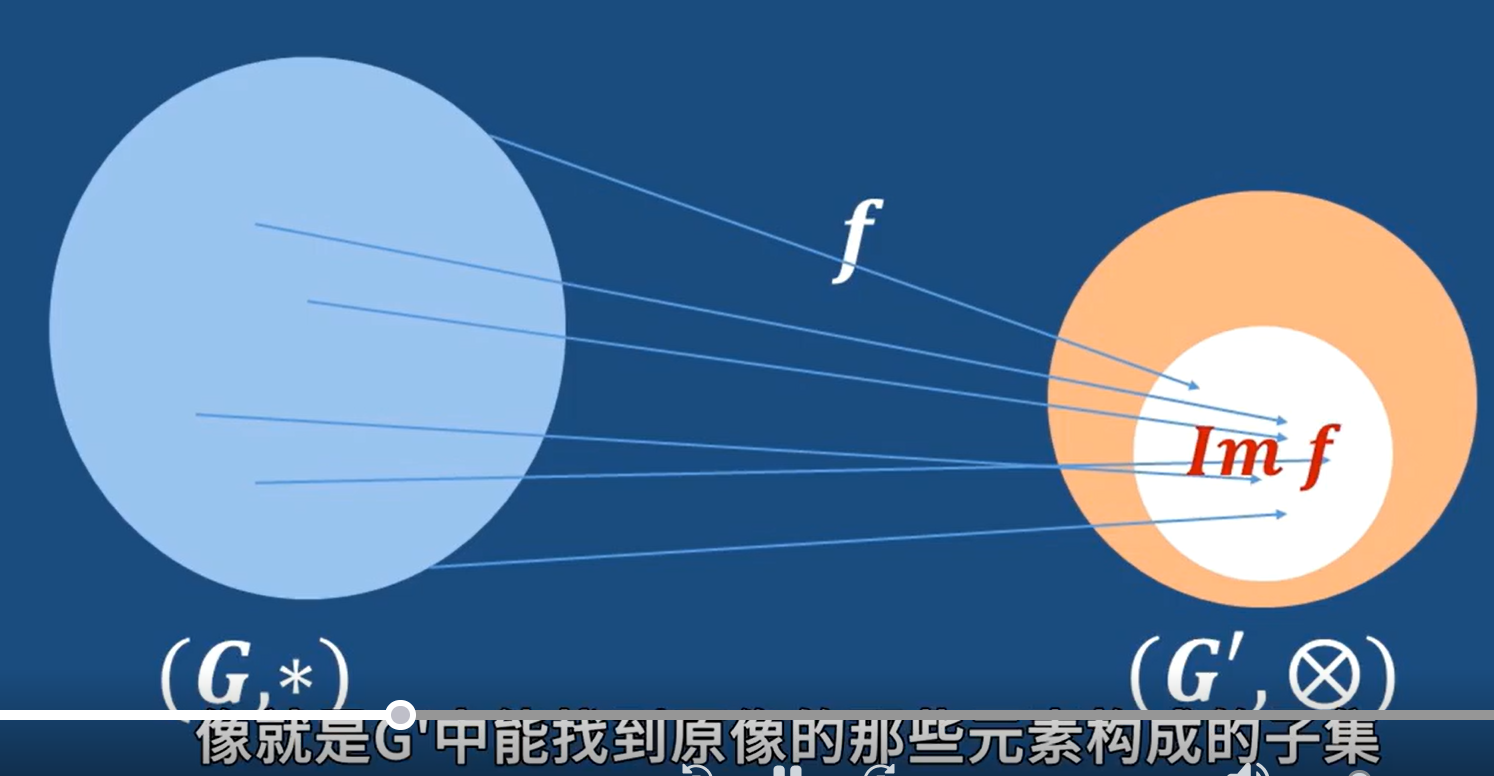
- 同態核:
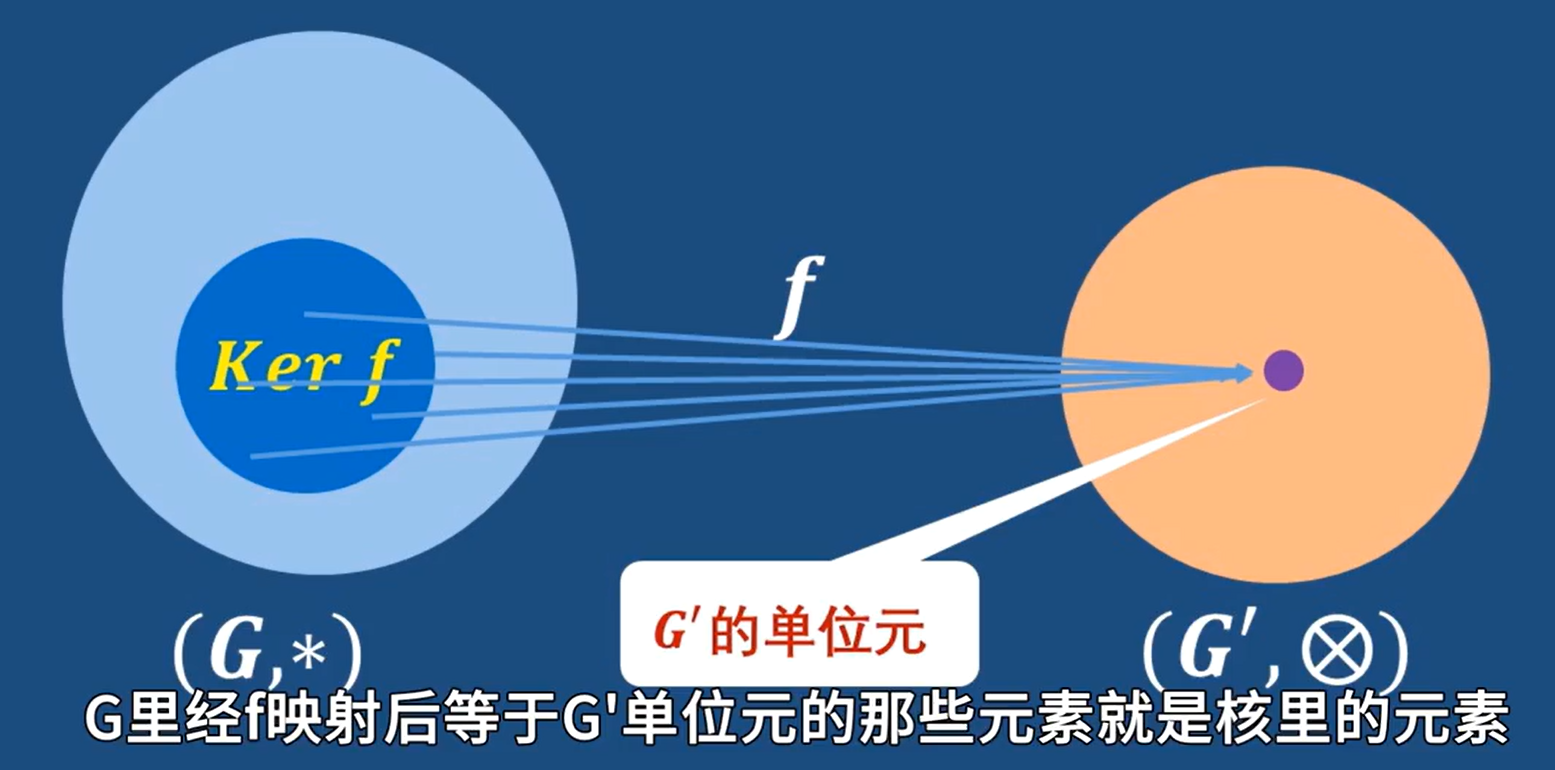
符號表示:

- 嵌入映射
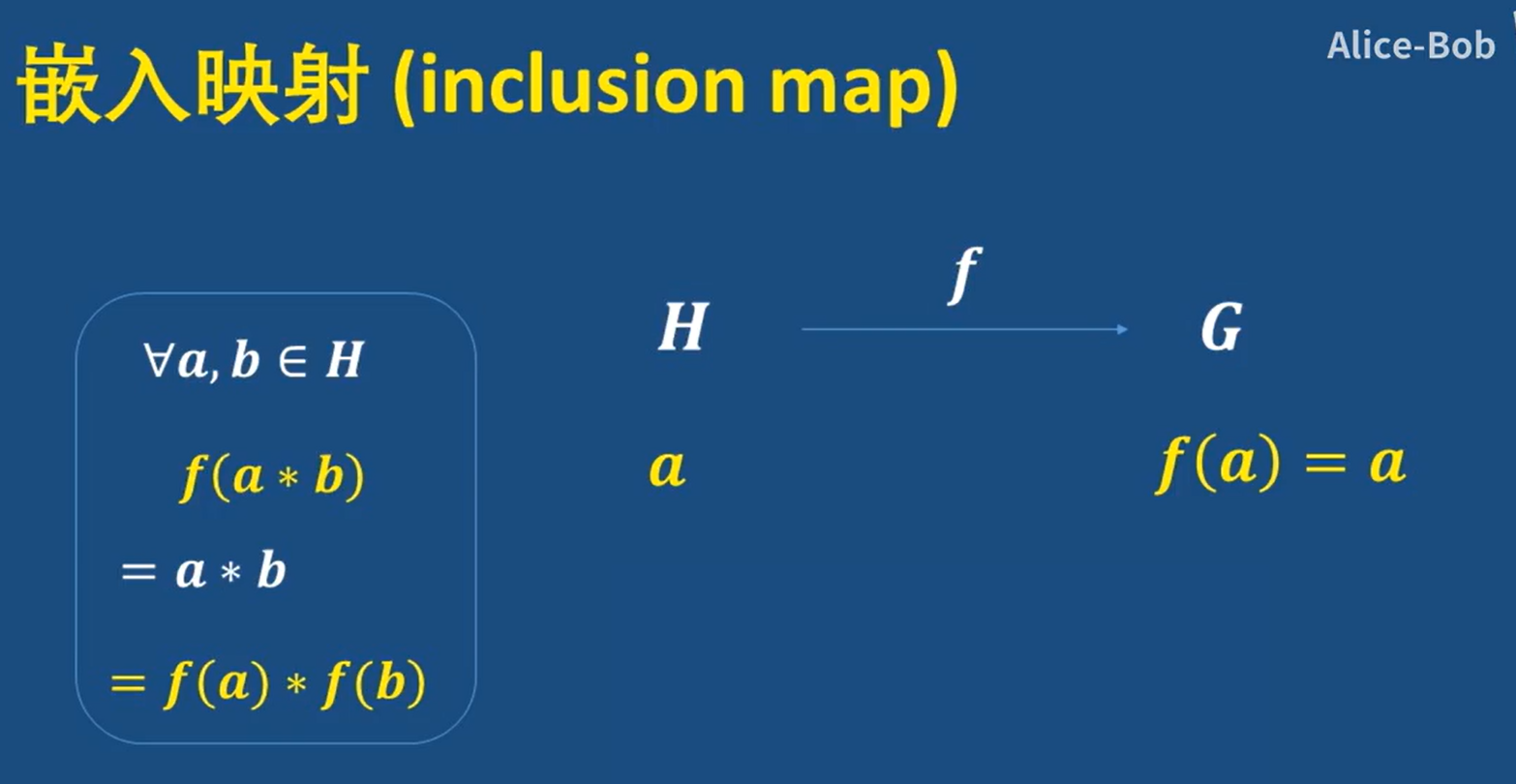
其中H是G的子集,這就相當于是子群到群的映射,并且原像到像之間是一一對應的,所以這是一個單射,也可以叫作單一同態
- 自然映射
N是G的正規子群
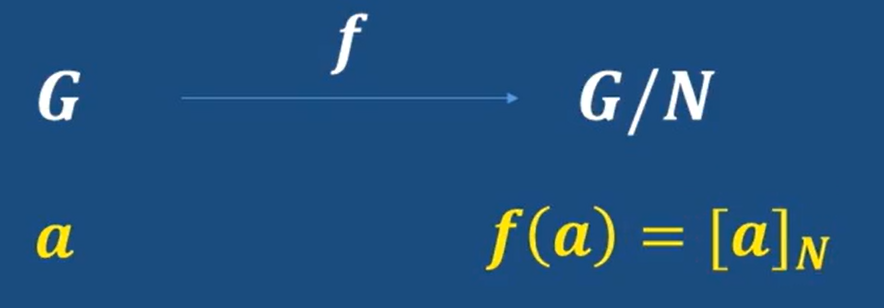
每個元素a會通過函數映射到相應的陪集

-
m次方映射
-
雅可比映射
幾個性質:利用一個群的知識去分析另一個群
- 單位元穿越后仍然是單位元
理論證明:

- 逆元穿越后仍然互為逆元

理論證明:
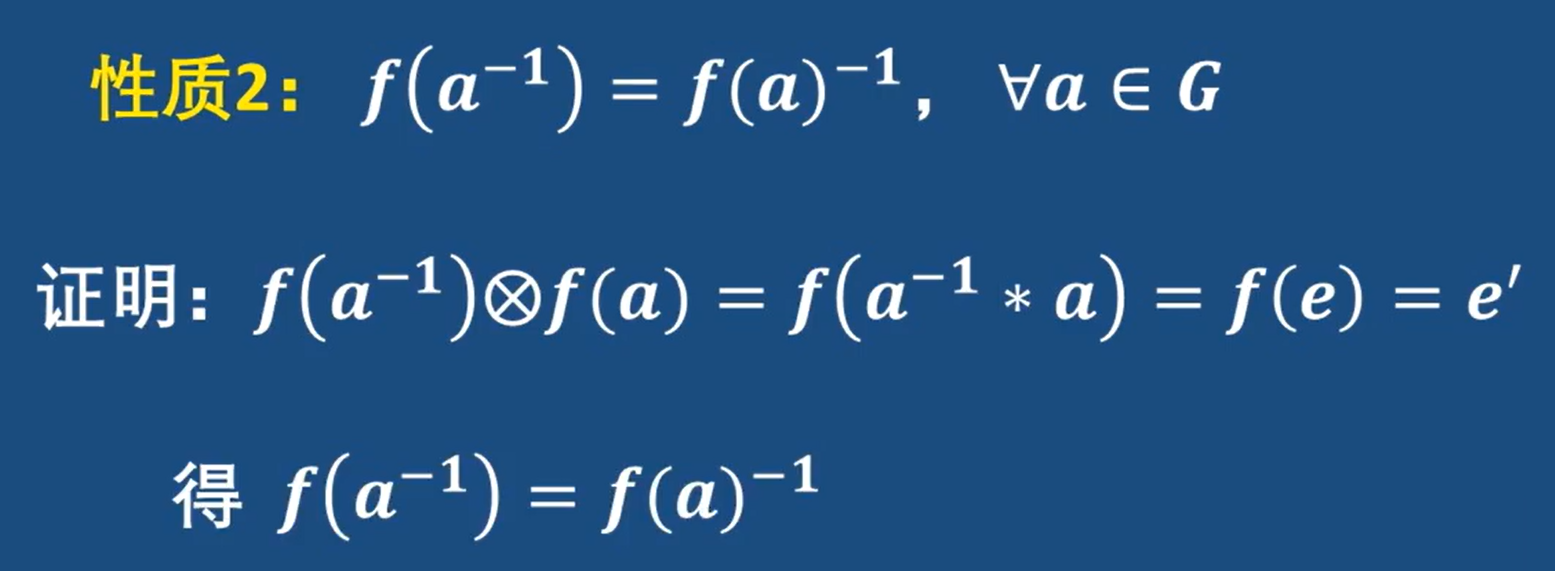
- 子群
理論證明:
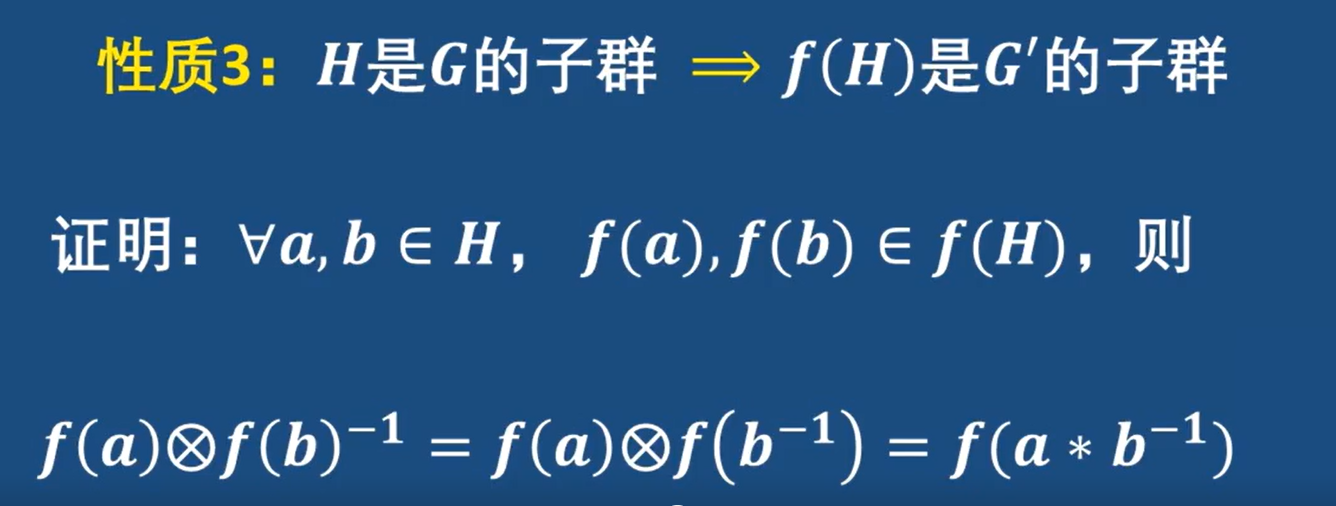
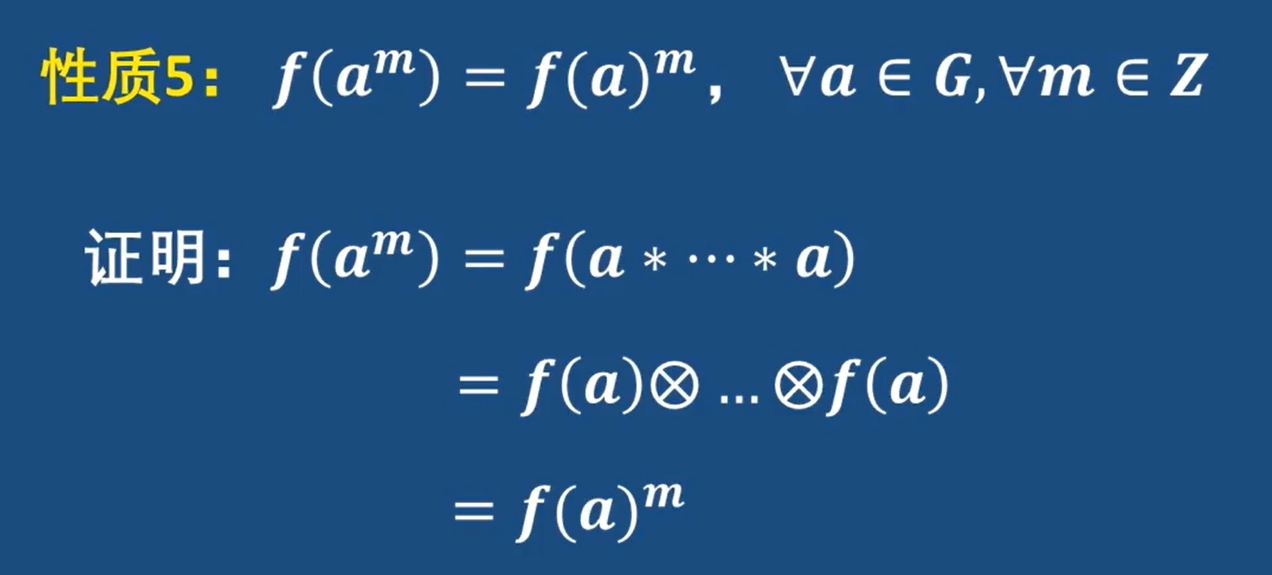
2-18 原根

“原根”存在的條件:(因為模n下并不一定有原根)

只有當n滿足上面這五種情況之一 才會存在原根
舉個反例:RSA算法,其模數n是兩個大素數的乘積,所以不存在原根
一些性質:

Zn*中的元素為phin個 所以其階也就是phin
這樣原根的階和Zn*的階相同,這樣原根就可以生成Zn* 的所有元素


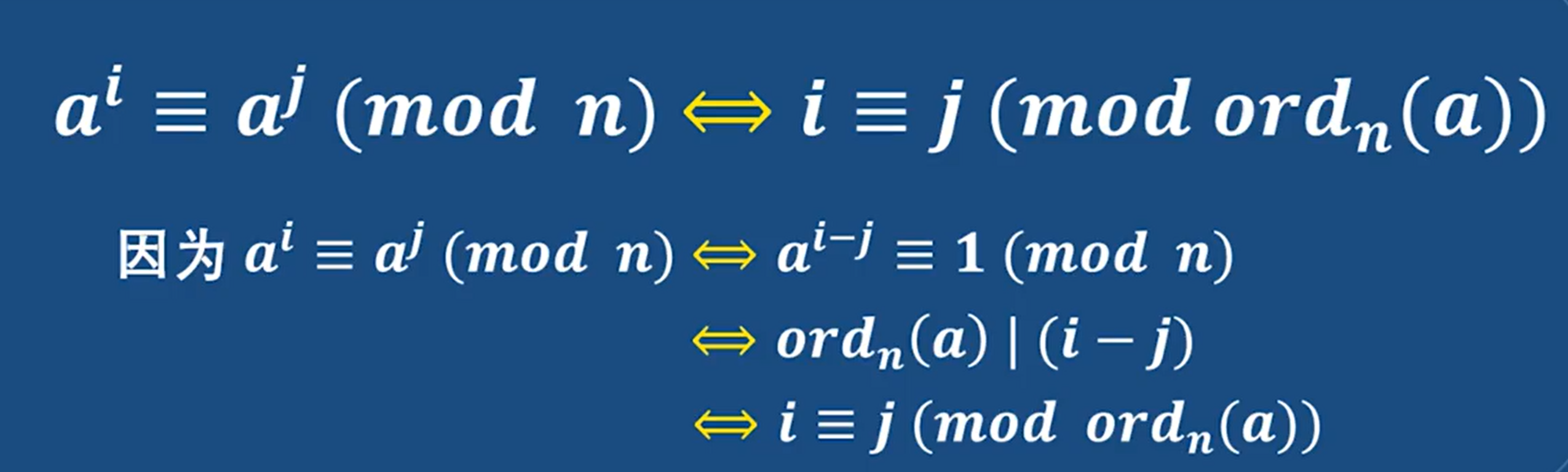










如何找原根:
方法:
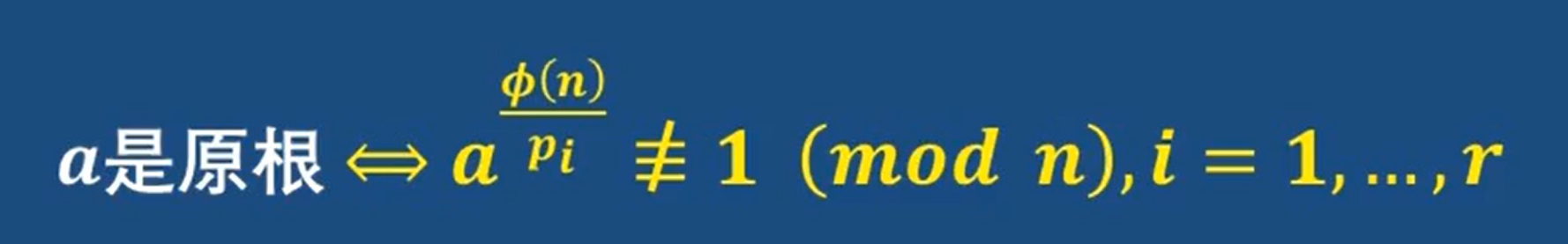

舉個例子:

這樣可以得知 2是模19下的原根
2-21 什么是環
代數結構:
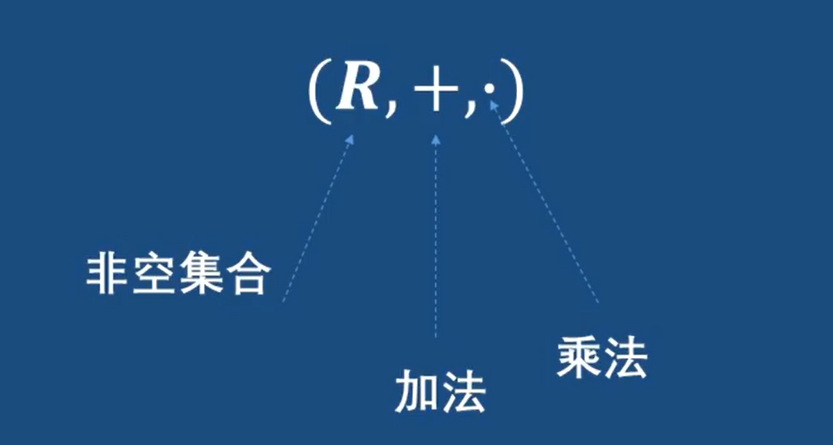
和群不同的是,這里有兩個二元運算符號,注意這里的加法和乘法都是抽象概念,不是真正的加減
環的定義:


分類:
- 有限環:環的元素數量是有限的
- 無限環:環的元素數量是無限的
舉例:



一些符號表示

尤其關注一下加法逆元的表示為負數
運算性質:

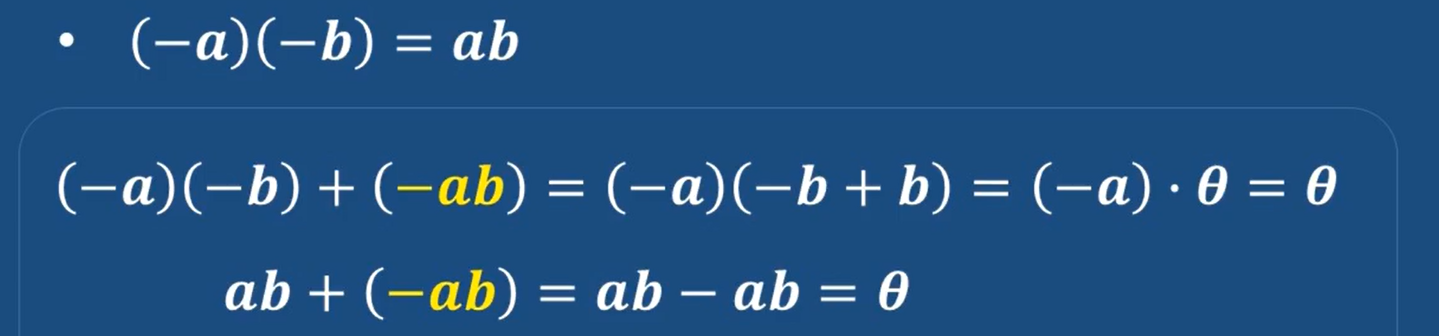

2-23 什么是域
繼承環,引出一下域
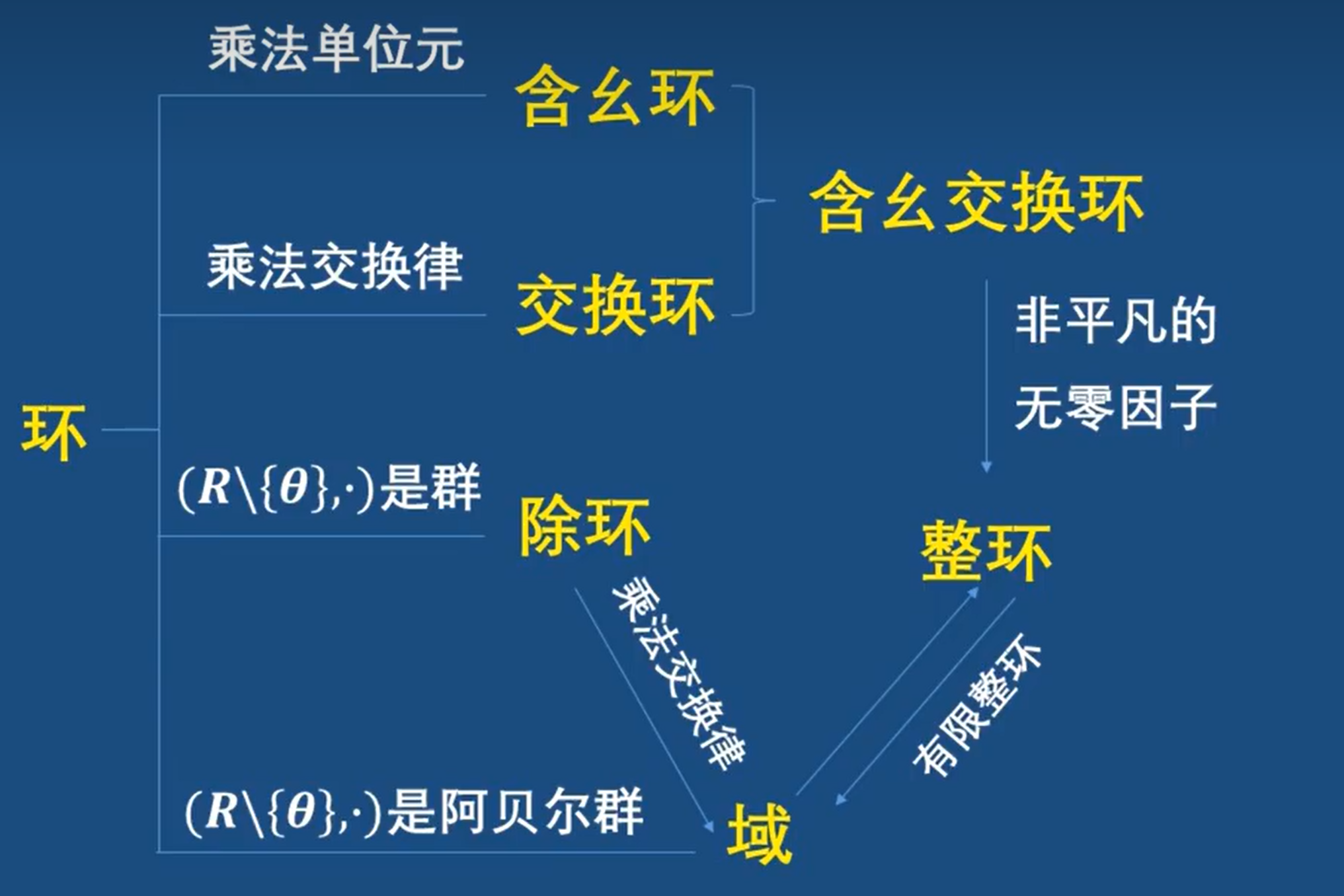
域的定義

整環和域的對比
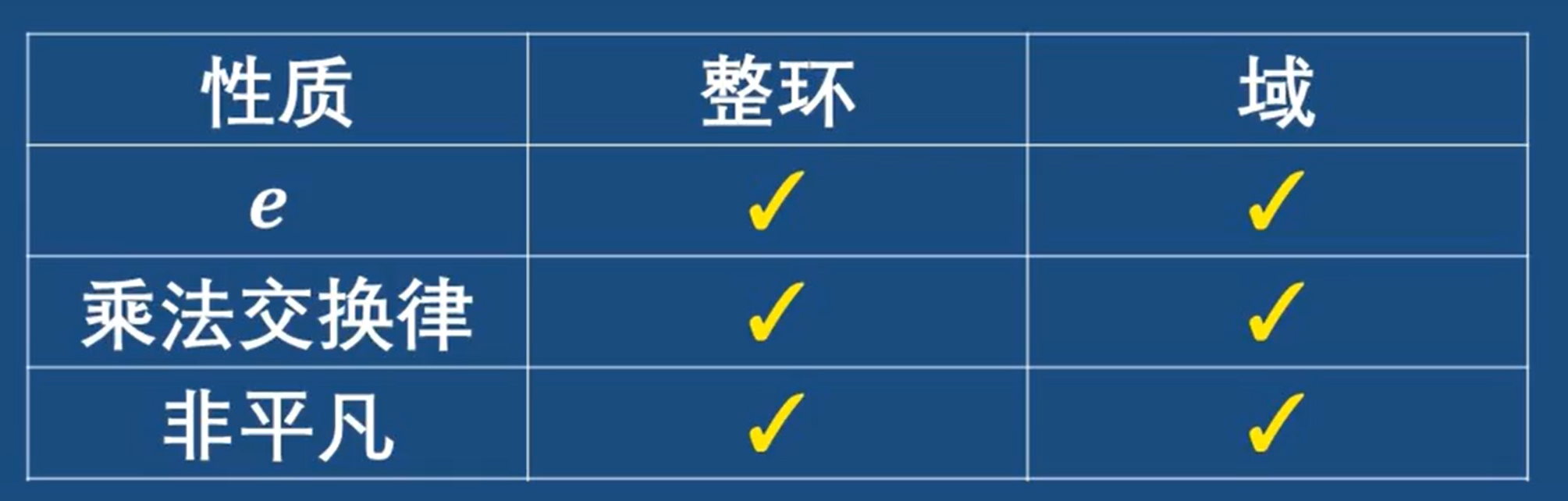
解釋一下域的非平凡原因:
因為域有加法和乘法兩個群,作為環的一種,域必然有零元
而非零元素要形成乘法阿貝爾群,那非零元素這部分就不能是空集
也就是說除了零元以外,域必然有其他元素,故域是非平凡的




2-25 子環
子環的定義:(類似群和子群的定義

特殊性質:

舉例:


mZ和Z在相同的運算下構成環,mZ里的整數都是Z的倍數,是Z的非空子集
特殊點:

Zn的元素其實都是剩余類,而不是整數,和Z里的并不是同一種東西;其中的運算也不同,Zn的是剩余類之間的運算,而Z則是普通的乘法和加法
如何判斷是不是子環?
核心原則:只要非空子集在環的運算下構成阿貝爾群和半群即可
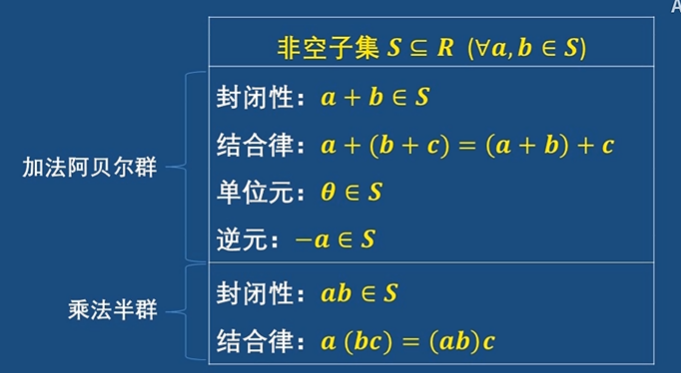
注意:
-
分配律不需要考慮,因為環滿足分配律,它的非空子集必然也滿足
-
乘法結合律也不用考慮,既然環滿足,其非空子集必然也滿足
-
加法的結合律也不用考慮
綜上,可以得到一種簡化版本的判斷方法,如下:

其實關于零元也可以再簡化,因為其他條件中已經暗含

即為:

但是利用子群的判斷可以進一步簡化,最簡方法
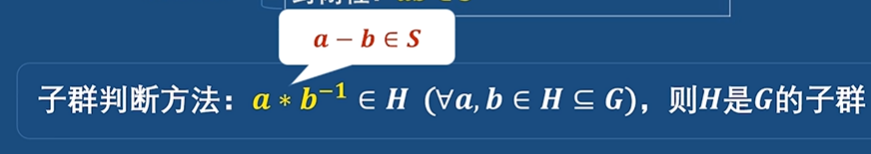



擴充:

舉例:

注意事項:


非平凡的例子:

2-26 理想
介紹一下理想的本質:是一種特殊類型的子環

定義:

如何判斷是不是理想:

簡化逆元

關于定理:
為什么理想是子環

舉例:


不斷碰撞服務社會,占領了整個姐的底盤。
注意點:


都有單位元,都是矩陣,但是單位元不同
補充簡單概念:

2-32 多項式環
類比學習:初中學的多項式建立在實數的基礎上,幾個單項式的和叫做多項式
在任意環上都可以建立多項式,這也是環比群強大的一個具體表現,因為多項式需要兩種運算,而群只有一種
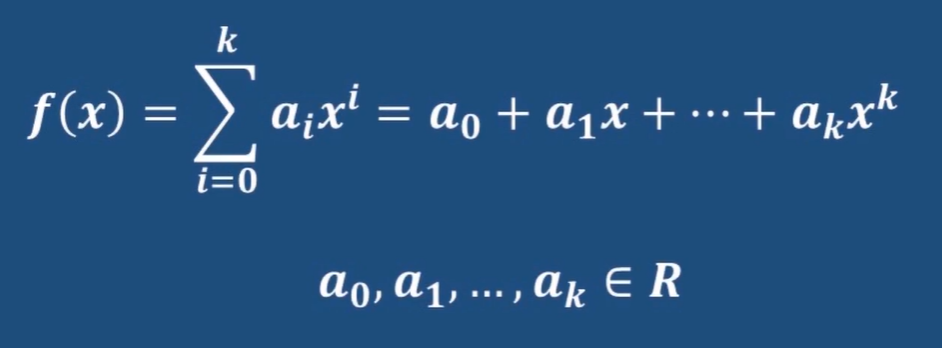
這里面a是多項式的系數,k是非負整數,叫多項式的度;變量x稱為環上的不定元,也就是變量
當系數為零元時,相應的單項式可以省略不寫;當系數為單位元e時,相應的單項式可以不寫系數了
- 多項式環 定義:

基礎加法和乘法運算和初中實數多項式類似
但是需要注意:
因為環不一定滿足乘法交換律

- 常數多項式

關于度的性質:

- 其他性質

證明:
證明不是域 反證法
大學的思維對待


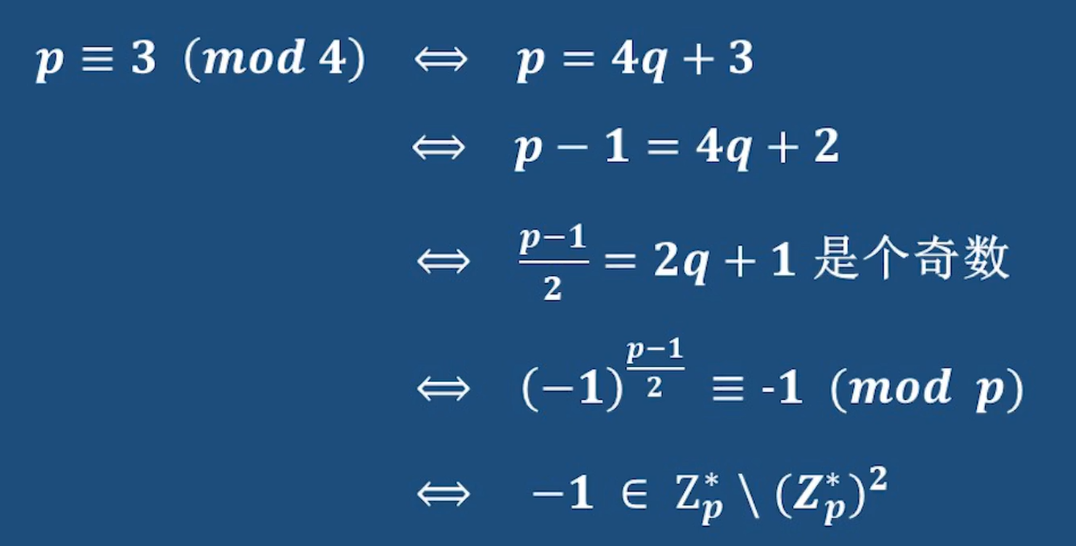

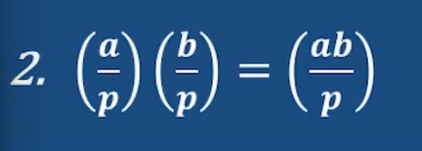
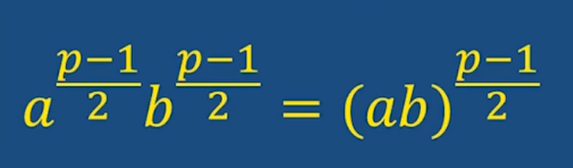
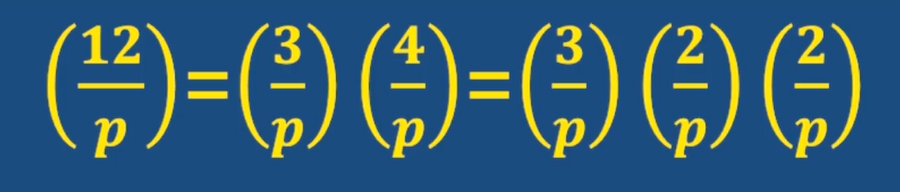
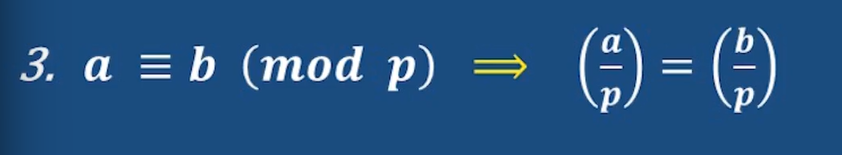




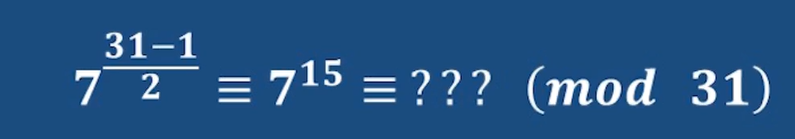
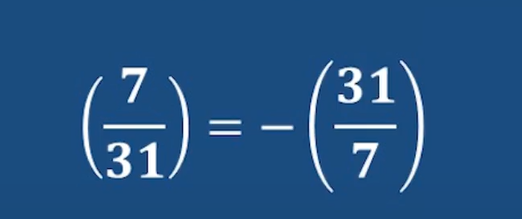
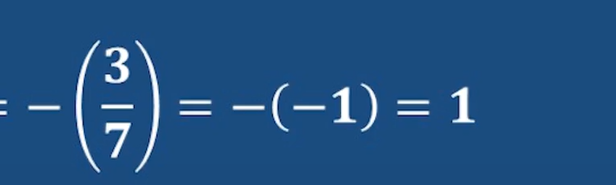

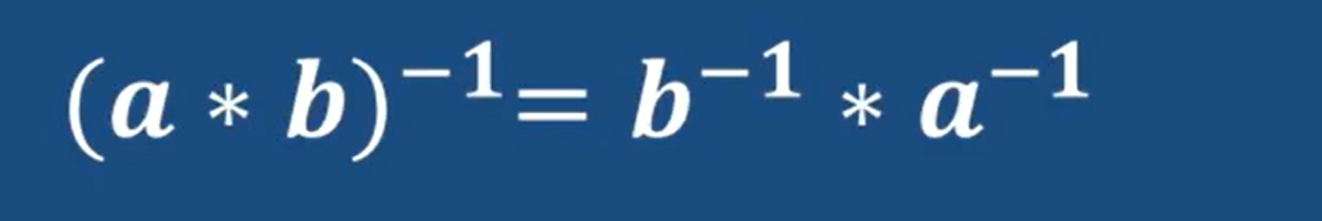
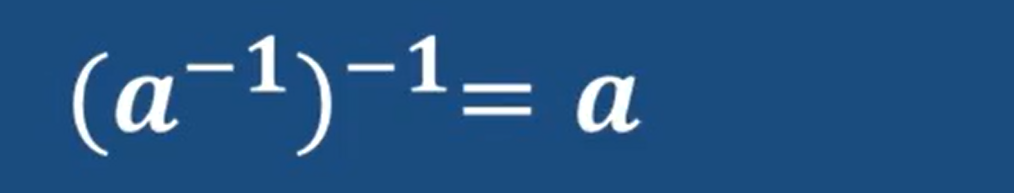
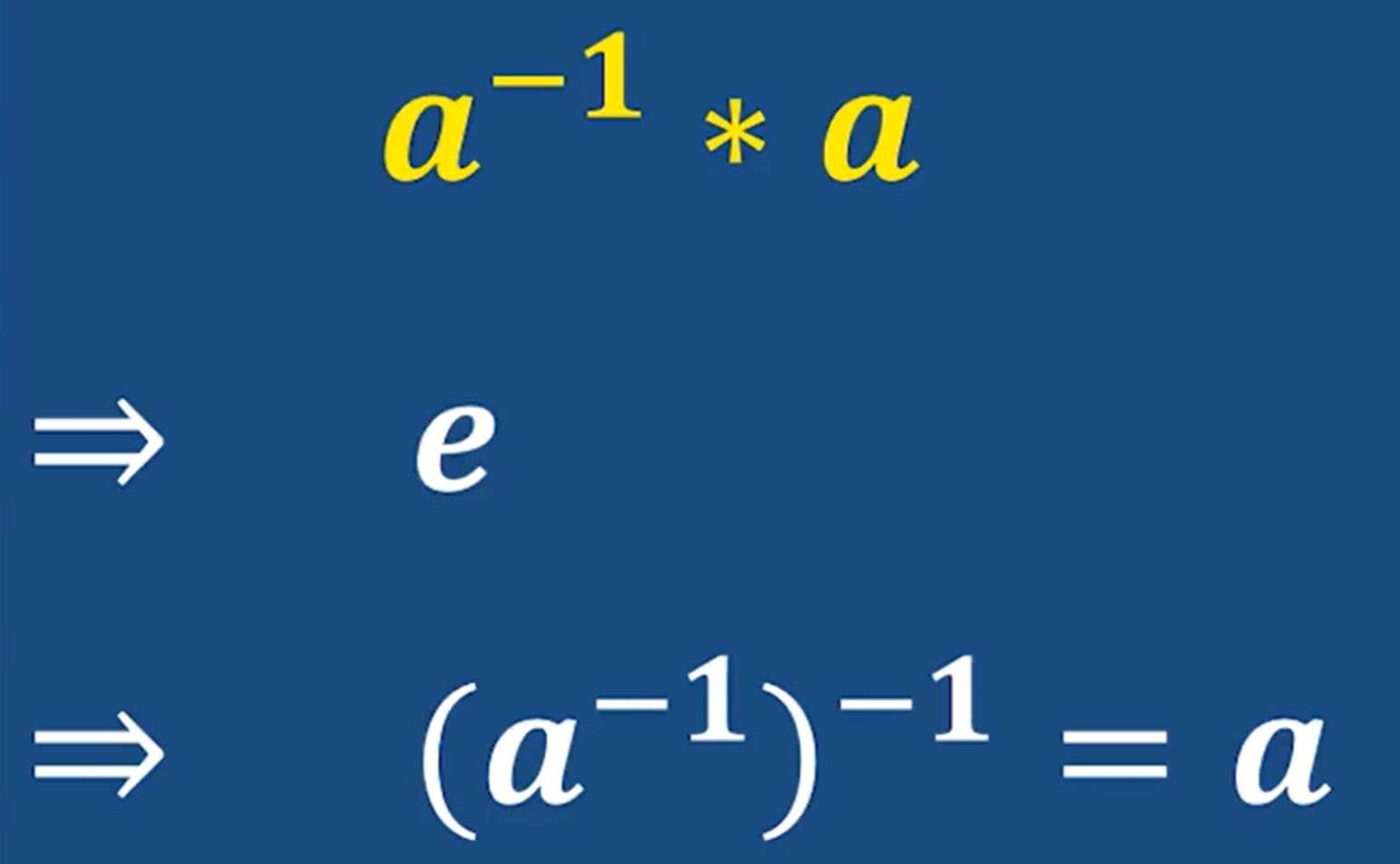

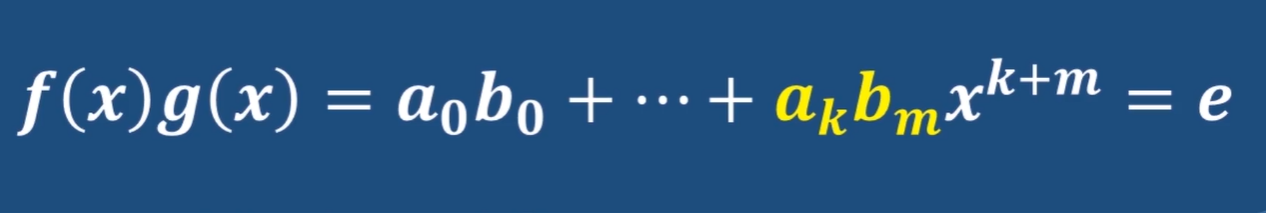




(官網無法下載visual studio 2019安裝包))

)

)




)




——模擬+優先隊列(小根堆)、排序+交換)
