嘎嘎詳細的三維變換詳細講解，包括視圖變換、投影變換等，超級通俗易懂！

前置二維空間的各種變換筆記：二維變換

三維空間中的齊次坐標

從二維變換開始引申，可得到三維中的一個點的表達方式為 $(\mathbf{x}, \mathbf{y}, \mathbf{z}, 1)^{\top}$ ，也就是w=1，而三維的向量則表達為 $(\mathbf{x}, \mathbf{y}, \mathbf{z}, 0)^{\top}$ ，也就是w=0
由于三維空間的一個點是上述格式的，若其中的w由于兩點相加或者其他原因超過了1，則我們令這個點的xyz都除以w，那么w就會變成1了，也就是xyz所表達的位置坐標為 $(x / w, y / w, z / w)$
而在三維空間中的齊次變換矩陣則如 $\left(\begin{array}{l} x^{\prime} \\ y^{\prime} \\ z^{\prime} \\ 1 \end{array}\right)=\left(\begin{array}{lllc} a & b & c & t_x \\ d & e & f & t_y \\ g & h & i & t_z \\ 0 & 0 & 0 & 1 \end{array}\right) \cdot\left(\begin{array}{l} x \\ y \\ z \\ 1 \end{array}\right)$ 所示
其中矩陣的abcdefghi表達為線性變換，tx、ty、tz表達為平移變換，總體表達為一種仿射變換。
同樣，矩陣的最后一行也是（0, 0, 0, 1）
其中線性變換和平移變換的執行順序是先執行線性變換，再執行平移變換，具體可以從我們二維仿射變換公式看 $\binom{x^{\prime}}{y^{\prime}}=\left(\begin{array}{ll} a & b \\ c & d \end{array}\right) \cdot\binom{x}{y}+\binom{t_x}{t_y}$ ，先乘線性變換矩陣，再加平移變換。

三維齊次變換

由二維向外引申，便可得到三維的各種變換矩陣形式
縮放變換： $\mathbf{S}\left(s_x, s_y, s_z\right)=\left(\begin{array}{cccc} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$
平移變換： $\mathbf{T}\left(t_x, t_y, t_z\right)=\left(\begin{array}{cccc} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{array}\right)$
旋轉變換：
- 繞x軸旋轉： $\mathbf{R}_x(\alpha)=\left(\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha & 0 \\ 0 & \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$
- 繞y軸旋轉： $\mathbf{R}_y(\alpha)=\left(\begin{array}{cccc} \cos \alpha & 0 & \sin \alpha & 0 \\ 0 & 1 & 0 & 0 \\ -\sin \alpha & 0 & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$
- 繞z軸旋轉： $\mathbf{R}_z(\alpha)=\left(\begin{array}{cccc} \cos \alpha & -\sin \alpha & 0 & 0 \\ \sin \alpha & \cos \alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$
- 上述旋轉都是簡單的繞軸旋轉，但是如果是一般性的旋轉又該怎么處理呢？
- 圖形學有一個大佬，就寫了一個矩陣，可以把任意一個軸的旋轉寫成一個矩陣，這個旋轉公式就是著名的Rodrigues旋轉公式，公式為 $\mathbf{R}(\mathbf{n}, \alpha)=\cos (\alpha) \mathbf{I}+(1-\cos (\alpha)) \mathbf{n} \mathbf{n}^T+\sin (\alpha) \underbrace{\left(\begin{array}{ccc} 0 & -n_z & n_y \\ n_z & 0 & -n_x \\ -n_y & n_x & 0 \end{array}\right)}_{\mathbf{N}}$
- 其中n代表要繞著的旋轉軸向量

圖形變換

模型變換：類比于在一個場景中，模型的擺放，也就是拍照時所拍的物體放在哪
視圖變換：類比于，找到一個相機的角度，也就是相機在哪里拍照
投影變換：從模型和視圖變換之后做一個3d到2d的投影，類似與相機和拍攝物體都確定好了，拍照的這么個過程

視圖變換如何做？

也就是怎么定義一個相機視角
首先需要相機的位置 $\vec{e}$ ，其次還需要相機的朝向 $\hat{g}$ ，也就是往哪看，最后需要一個向上方向 $\hat{t}$ 來定義相機是往上看還是往下看。至此，即可確定一個相機的視角了。
由于只要能保住相機和其所拍攝的物體所有的相對位置都是固定的，那么無論相機和這個物體被怎樣移動，那么最后拍攝下來的照片應該都是一樣的才對，所以為了方便運算，有一個約定俗成的規定，就是將相機永遠擺放至原點
假設當前相機視角如圖所示，應該怎樣將其變換到原點出呢
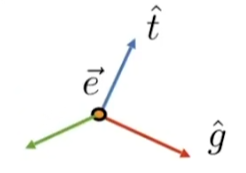
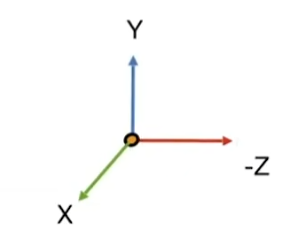
- 首先做一個平移變換將相機移動到原點
- 再將相機朝向 $\hat{g}$ 做旋轉變換移動到-Z上
- 最后將向上朝向 $\vec{t}$ 移動到Y上，那么 $\times t$ 也就自動朝向X了
- 我們可以定義整個變換矩陣為M，也就是用M來表達剛剛的所有操作，那么就有 $M_{\text {view }}=R_{\text {view }} T_{\text {view }}$
- 也就是先乘平移變換再乘旋轉變換即可得到總的M變換矩陣，而這個變換矩陣T很好寫，為 $T_{\text {view }}=\left[\begin{array}{cccc} 1 & 0 & 0 & -x_e \\ 0 & 1 & 0 & -y_e \\ 0 & 0 & 1 & -z_e \\ 0 & 0 & 0 & 1 \end{array}\right]$ ，也就是將自己的所在點各減去自己點離原點的距離即可
- 而旋轉R矩陣則相對較難，很難直觀的知道怎樣從一個軸變換到X、Y、-Z軸上，但是我們如果反過來思考，如果要把X、Y、-Z軸變換到某一個軸上，就很簡單了，這就是前文提到的逆變換，而我們知道，逆變換矩陣是一個正交矩陣，而正交矩陣有一個性質就是他的逆是他自己的轉置 $\mathbf{R}_{-\theta}=\mathbf{R}_{\theta}^T$ ，于是我們只需要求出X、Y、Z如何變換到 $g\times t$ 、 $t$ 和 $? g$ 上，再對該矩陣轉置一下，就能得到從 $g\times t$ 、 $t$ 和 $g$ 變換到X、Y、-Z的變換矩陣了。
- 比如要將X軸 $\begin{bmatrix} 1\\ 0\\ 0\\ 0 \end{bmatrix}$ 旋轉到 $\times t$ 軸 $\begin{bmatrix} x_{\hat{g} \times \hat{t} }\\ y_{\hat{g} \times \hat{t} }\\ z_{\hat{g} \times \hat{t} }\\ 0 \end{bmatrix}$ 上，則旋轉矩陣為 $\left[\begin{array}{cccc} x_{\hat{g} \times \hat{t}} & 0 & 0 & 0 \\ y_{\hat{g} \times \hat{t}} & 0 & 0 & 0 \\ z_{\hat{g} \times \hat{t}} & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]$ ，同理可得Y、Z軸，將其合并一下，即可得到總的逆旋轉矩陣 $R_{view}^{-1}=\left[\begin{array}{cccc} x_{\hat{g} \times \hat{t}} & x_t & x_{-g} & 0 \\ y_{\hat{g} \times \hat{t}} & y_t & y_{-g} & 0 \\ z_{\hat{g} \times \hat{t}} & z_t & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]$ ，則轉置后的旋轉矩陣為 $R_{view}=\left[\begin{array}{cccc} x_{\hat{g} \times \hat{t}} & y_{\hat{g} \times \hat{t}} & z_{\hat{g} \times \hat{t}} & 0 \\ x_t & y_t & z_t & 0 \\ x_{-g} & y_{-g} & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]$ ，這便得到了從任意軸旋轉到原點X、Y、-Z軸的旋轉矩陣了，再和前面的平移矩陣T相乘，即可得到最終的變換矩陣M。
也就是，只要相機和所拍攝關聯到的物體都按照這個M矩陣進行變換，那么在變換前和變換后所拍攝到的內容應該都是一樣的。

投影變換如何做？

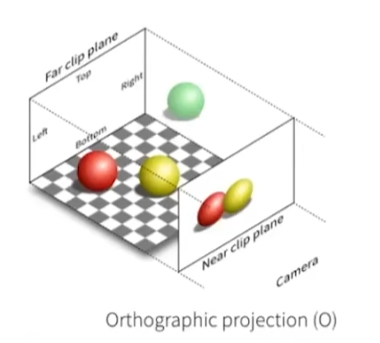
正交投影：投影前后無透視扭曲，即無近大遠小的特性
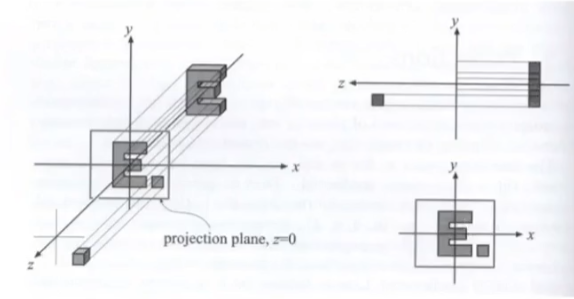
- 而想要將三維物體在無透視變化的情況下投影到二維平面上其實很簡單，只需要去除這個物體的z軸就行了
- 假設我們要投影的物體如上所示，可以發現，只要將他倆的z軸去掉，那么剩下的x，y自然就是他在二維平面上的投影。
- 但是一般情況下，需要先將這個物體通過變換矩陣轉移到原點xy軸的-1到1之間的矩形之中，這樣做的目的是為了簡化后續操作，也就是大家都遵守這套規范，后續api啊各方面的開發就會很簡便。
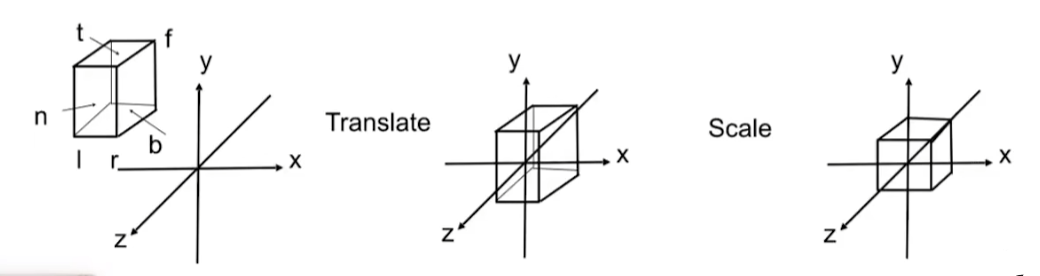
- 但是這樣做就會出現一個問題，就是物體的前后信息丟失了，你無法顯示出物體的深度信息，為了解決這個問題，通常會保留下這個z軸，也就是說先將物體通過各種變換轉移到原點處xyz都在-1到1的一個立方體中，這個立方體也叫做標準化空間，這樣的話物體之間的深度信息就會保留下來，也就是x和y坐標會被用來確定物體在屏幕上的位置，而z坐標則用于深度測試等目的。而最終的三維到二維的投影呢則是對這個標準化空間里做一個切片，z坐標被用來進行深度測試和裁剪，而x和y坐標則被用來確定最終在屏幕上的位置。也就是如下圖所示。
- 其中l、r為物體的左右（left、right），b、t為下上（bottom、top），f、n為遠近（far，near）。
- 而將被拍攝物體通過變換矩陣到原點的-1到1的空間內也就很簡單了，先平移變換，再縮放變換即可（對應著上圖的二圖和三圖）。
- 平移變換可以直接將物體的中心處移動到原點處即可，而物體的中心計算方法就很簡單，x軸的中心就是 $\frac{r+l}{2}$ ，yz軸同理，那么將物體最終移動到中心就是自身每個軸減去這個值即可，于是平移變換矩陣為 $\left[\begin{array}{cccc} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{array}\right]$
- 而縮放變換呢就是要將物體規范化到-1到1的空間內，-1到1的長度為2，那么x軸的縮放就是用2除以物體的寬度，也就是 $\frac{2}{r-l}$ （具體數學推理就是求一個線性變換y=ax+b，將x等于l和r代入即可得到a和b的值，其中a就是縮放因子，b就是平移因子，最后解的a就是這個2/(r-l)），其他軸同理，于是縮放矩陣為 $\left[\begin{array}{cccc} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]$
- 而最終的正交投影變換矩陣為他倆相乘 $M_{\text {ortho }}=\left[\begin{array}{cccc} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{cccc} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{array}\right]=\left[\begin{array}{cccc} \frac{2}{r-l} & 0 & 0 & -\frac{r+l}{2} \\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{2} \\ 0 & 0 & \frac{2}{n-f} & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{array}\right]$
- 最后通過這個矩陣M就可以將任意物體規范化到原點處-1到1的標準空間中啦~
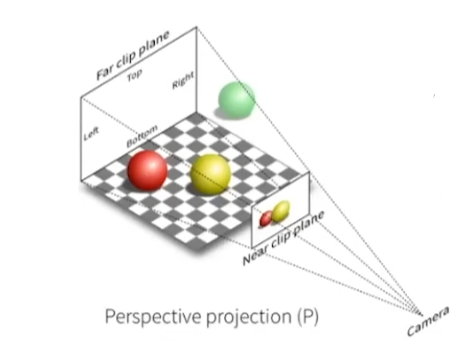
透視投影：有近大遠小的特性
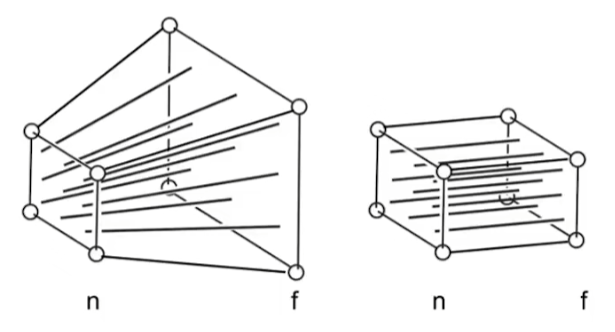
- 將三維物體通過透視投影到二維平面上有一個辦法，由于透視投影他可以理解成沿著一個點，向外延申出四條線，如上圖，那么所包裹住的物體就是一個四棱臺，而我們知道，正交投影所包裹住的是一個長方體，那我們就可以先將這個四棱臺壓成長方體，再按照正交投影的辦法去變換即可。
- 也就是將上面左圖的遠平面在xy軸處壓成近平面的矩形，最終呈現右圖的樣子。顯然，在這個變化當中，近平面的x、y、z都不會發生改變，而遠平面的z和遠平面中心點也不會發生改變。
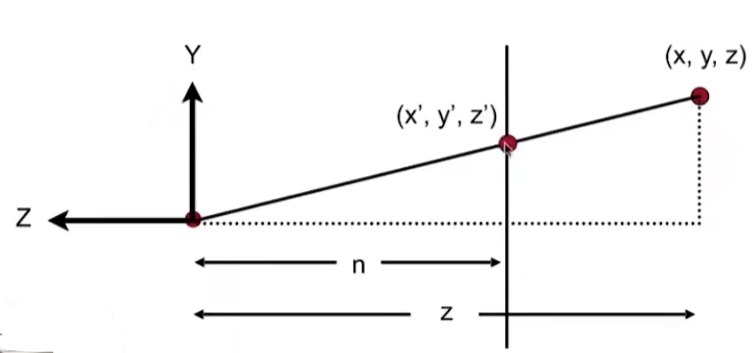
- 如上圖所示（(x’,y’,z’)是近平面的點，(x,y,z)是遠平面的點），根據相似三角形原則，若點(x,y,z)想變換到點(x’,y’,z’)上，y和y’的比值一定等于n和z的比值，于是可得 $y^{\prime}=\frac{n}{z} y$ ，同理可得 $x^{\prime}=\frac{n}{x} y$
- 也就是說原本(x,y,z,1)和一個矩陣相乘后，會得到(nx/z,ny/z,不知道,1)這樣的向量，而我們知道，在齊次坐標中，一個點同乘任何非0常數，所表達的矩陣依然一致，也就是(nx/z,ny/z,不知道,1)和(nx,ny,不知道,z)他倆所表達的點都是(x,y,z)，也就是 $M_{\text {persp } \rightarrow \text { ortho }}^{(4 \times 4)}\left(\begin{array}{l} x \\ y \\ z \\ 1 \end{array}\right)=\left(\begin{array}{c} n x \\ n y \\ \text { unknown } \\ z \end{array}\right)$
- 很容易就能得到這個M矩陣為 $M_{\text {persp ortho }}=\left(\begin{array}{cccc} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & 1 & 0 \end{array}\right)$
- 而上述矩陣中的第三行的值可以通過前面所說的兩個條件來計算，就是“近平面的x、y、z都不會發生改變，而遠平面的z和遠平面中心點也不會發生改變。”
- 設近平面的z軸值為n，也就是上面的M矩陣乘上近平面的(x,y,n,1)后仍然是(x,y,n,1)，然后在這個齊次坐標同乘一個n，也就是 $M_{\text {persp } \rightarrow \text { ortho }}^{(4 \times 4)}=\left(\begin{array}{l} x \\ y \\ n \\ 1 \end{array}\right)==\left(\begin{array}{c} n x \\ n y \\ n^2 \\ n \end{array}\right)$
- 那么此時我們將M矩陣的第三行當個向量提取出來，也就是 $\left(\begin{array}{llll} 0 & 0 & A & B \end{array}\right)\left(\begin{array}{l} x \\ y \\ n \\ 1 \end{array}\right)=n^2$ ，前面兩個數之所以為0是因為很明顯最后的這個 $n^2$ 肯定和xy無關，相乘后也就是 $A n+B=n^2$ 。
- 而遠平面的中心點在變換中不會發生改變，設遠平面的z軸值為f，而遠平面中心點則表示為 $\left(\begin{array}{l} 0 \\ 0 \\ f \\ 1 \end{array}\right)$ ，同時乘個f，則為 $\left(\begin{array}{c} 0 \\ 0 \\ f^2 \\ f \end{array}\right)$ ，和前面的 $\left(\begin{array}{llll} 0 & 0 & A & B \end{array}\right)$ 相乘后也就是 $A f+B=f^2$ ，解兩式可得 $\begin{aligned} & A=n+f \\ & B=-n f \end{aligned}$
- 這樣就得到了最終的變換矩陣 $M_{\text {persp ortho }}=\left(\begin{array}{cccc} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{array}\right)$ ，這個矩陣可以將任意物體從透視投影的四棱臺擠壓成正交投影的正方形
- 最后再按照正交投影的方法來完成后續步驟即可完成透視投影 $M_{\text {persp }}=M_{\text {ortho }} M_{\text {persp } \rightarrow \text { ortho }}$