本文致力于闡述AdaBoost基本步驟涉及的每一個公式和公式為什么這么設計。
AdaBoost集成學習算法基本上遵從Boosting集成學習思想，通過不斷迭代更新訓練樣本集的樣本權重分布獲得一組性能互補的弱學習器，然后通過加權投票等方式將這些弱學習器集成起來得到性能較優的集成模型。

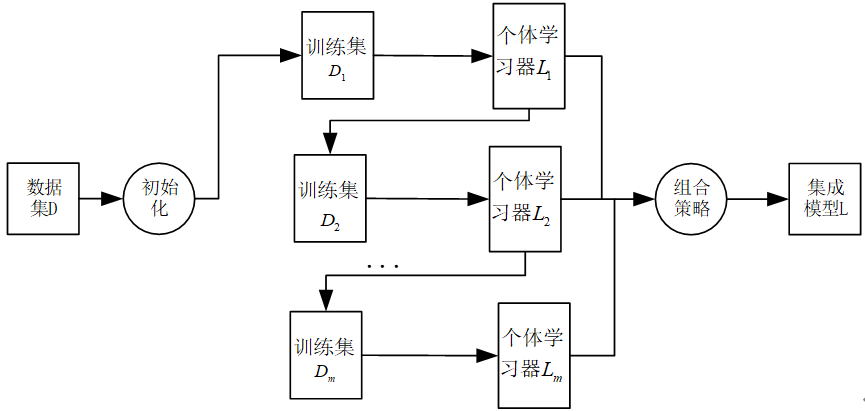
圖1：Boosting集成算法思想。
下面以二分類任務(標簽不是為-1，就是為+1)為例介紹該算法的具體過程。值得注意的是，下面的公式推導是以二分類任務下得出來，所以公式(比如樣本權重更新公式)才會顯得比較整潔，但如果換成其他任務，如多分類，那么公式會復雜很多。
對于訓練樣本集$D=\left(x_1,y_1\right),\left(x_2,y_2\right),\dots ,(x_n,y_n)$，其中標簽 y i ∈ { ? 1 , + 1 } y_i\in\left\{-1,+1\right\} yi?∈{?1,+1}，由AdaBoost集成學習算法構造集成模型的基本步驟如下：
（1）令$i=1$并設定弱學習器的數目m。對應第一次迭代，使用均勻分布初始化訓練樣本集的權重分布，令$n$維向量${\mathbf{w}}^i$表示第$i$次需更新的樣本權重，則有：
${\mathbf{w}}^1={\left(w_{11},w_{12},\dots ,w_{1n}\right)}^T={\left(\frac{1}{n},\frac{1}{n},\dots ,\frac{1}{n}\right)}^T$
（2）使用權重分布為${\mathbf{w}}^i$，此時$i=1$的訓練樣本集$D_i$學習得到第$i$個弱學習器$L_i$；
（3）計算$L_i$在訓練樣本集$D_i$上的分類錯誤率$e_i$：
$e_i={\sum }_{k=1}^n{w}_{ik}I\left(L_i\left(X_k\right)\ne y_k\right)$
（4）確定弱學習器$L_i$的組合權重${\alpha }_i$(${\alpha }_i$在最后得到最終的集成模型上用到)。由于弱學習器$L_i$的權重取值應與其分類性能相關，對于分類錯誤率$e_i$越小的$L_i$，則其權重${\alpha }_i$應該越大，故有：
${\alpha }_i=\frac{1}{2}\text{ln}\frac{1?e_i}{e_i}=\frac{1}{2}\text{ln}(\frac{1}{e_i}?1)$
可能會有人會為，為什么要這么設計${\alpha }_i$？我在下面給出了解釋。
（5）(重點)依據弱學習器$L_i$對訓練樣本集$D_i$的分類錯誤率$e_i$更新樣本權重，樣本權重更新公式為：
$w_{i+1,j}=\frac{w_{ij}\exp (?{\alpha }_i{y}_k{L}_i(x_k))}{Z_i}$
其中：
$Z_i={\sum }_{k=1}^n{w}_{ij}\exp (?{\alpha }_i{y}_k{L}_i(X_k))$
為歸一化因子，保證更新后權重向量為概率分布；
對權重更新公式的解釋：
回顧開頭，這是一個二分類任務，所以若樣本$(x_k,y_k)$分類正確，則要不$y_k=L_i(x_k)=1$，要不$y_k=L_i(x_k)=?1$，因此有$y_k?L_i(x_k)=1$**。**若樣本$(x_k,y_k)$分類錯誤，則要不$y_k=?1,L_i(x_k)=1$，要不$y_k=1,L_i(x_k)=?1$，因此有$y_k?L_i(x_k)=?1$。
因此公式
$w_{i+1,j}=\frac{w_{ij}\exp (?{\alpha }_i{y}_k{L}_i(x_k))}{Z_i}$
可以改寫
$w_{i+1,j}=\{\begin{array}{l}\frac{w_{ij}}{Z_i}\exp (?{\alpha }_i),y_k=L_i(x_k)\\ \frac{w_{ij}}{Z_i}\exp ({\alpha }_i),y_k\ne L_i(x_k)\end{array}$
這樣，對于錯誤的樣本會被放大$\frac{1?e_i}{e_i}$倍，以便在后續弱學習器構造過程得到應有的重視。
為什么是$\frac{1?e_i}{e_i}$倍？
$\frac{w_{i+1,j},y_k\ne L_i(x_k)}{w_{i+1,j},y_k=L_i(x_k)}=\frac{\frac{w_{ij}}{Z_i}\exp ({\alpha }_i)}{\frac{w_{ij}}{Z_i}\exp (?{\alpha }_i)}=\frac{\exp ({\alpha }_i)}{\exp (?{\alpha }_i)}=e^{2?{\alpha }_i}=e^{2?\frac{1}{2}\text{ln}\frac{1?e_i}{e_i}}=e^{\text{ln}\frac{1?e_i}{e_i}}=\frac{1?e_i}{e_i}$
另外$Z_i$的作用是歸一化，使得${\sum }_{j=1}^n{w}_{i+1,j}=1$
（6）若$i<m$，則令$i=i+1$并返回步驟（2），否則執行步驟（7）；
（7）對于$m$個弱分類器$L_1{,L}_2,\dots ,L_m$，分別將每個$L_i$按權重${\alpha }_i$進行組合：
$L=\text{sign}({\sum }_{i=1}^m{\alpha }_i{L}_i(X))$
得到并輸出所求集成模型$L$，算法結束。

參考資料：《機器學習及其應用》汪榮貴等編著