往期文章請點這里

往期文章請點 這里

Vector Space Models

在實際生活中，經常會出現以下兩種場景：
相同文字不同含義：

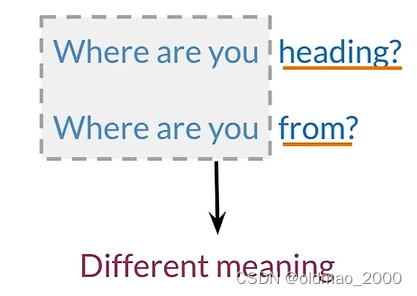
不同文字相同含義：

這些是之前的語言模型無法處理的問題，而向量空間模型不但可以區分以上場景，還能捕獲單詞之間的依賴關系。
You eat cereal from a bowl
麥片和碗是強相關
You buy something and someone else sells it
這里的買依賴于賣
這個優點使得向量空間模型可以用于下面任務：

著名語言學學者(Firth, J. R. 1957:11)說過：
“You shall know a word by the company it keeps”
指出了上下文對當前詞的表達有很大影響。

Word by Word and Word by Doc

構建共現矩陣（W/W and W/D 兩種），并為語料庫的單詞提取向量表示。

Word by Document Design

兩個不同單詞的共現是它們在語料庫中在一個特定的詞距內一起出現的次數。
Number of times they occur together within a certain distance $k$
例如，假設語料庫有以下兩個句子。

假設$k=2$，則單詞data的共現次數如下：

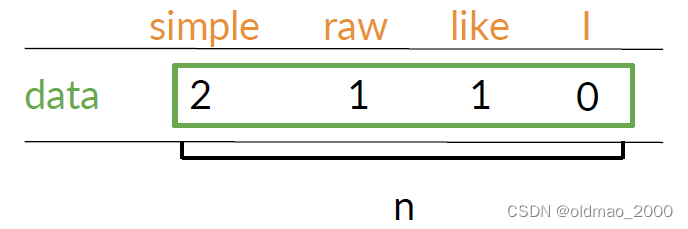
這里n取值在1到詞表大小之間。data和simple在第一句話距離是1，第二句話距離是2：

Word by Document Design

計算來自詞匯表的單詞在屬于特定類別的文檔中出現的次數。
Number of times a word occurs within a certain category
例如下圖中，語料庫包含三類文檔，然后可以計算某個單詞分別在三類文檔中出現的次數。

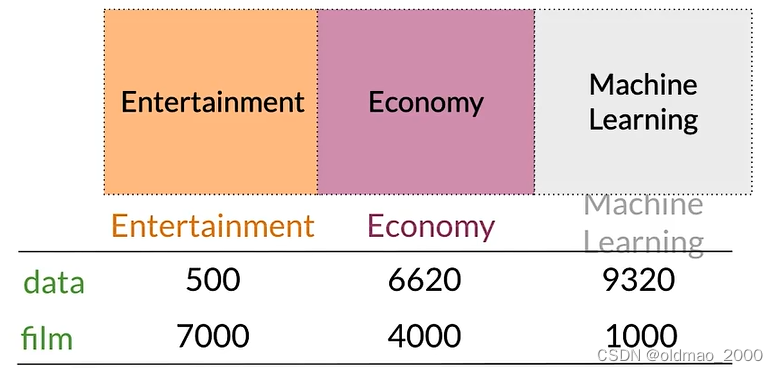
Vector Space

完成多組文檔或單詞的表示后，接下來可以構建向量空間。
以上面的矩陣為例

可以用行來表示單詞，列表示文檔，若以data和film構建坐標系，則可以根據矩陣中的數值得到向量表示：

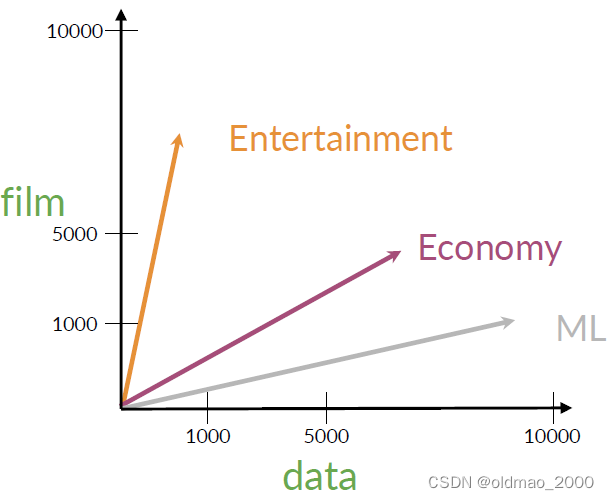
從向量空間表示中可以看到，economy的ML的文檔相似度要更大一些
當然這個相似度可以用計算Angle Distance來數字化度量。

Euclidean Distance

Euclidean Distance允許我們確定兩個點或兩個向量彼此之間的距離。
書接上回，假設有兩個語料的向量表示為：

放到二維空間中：

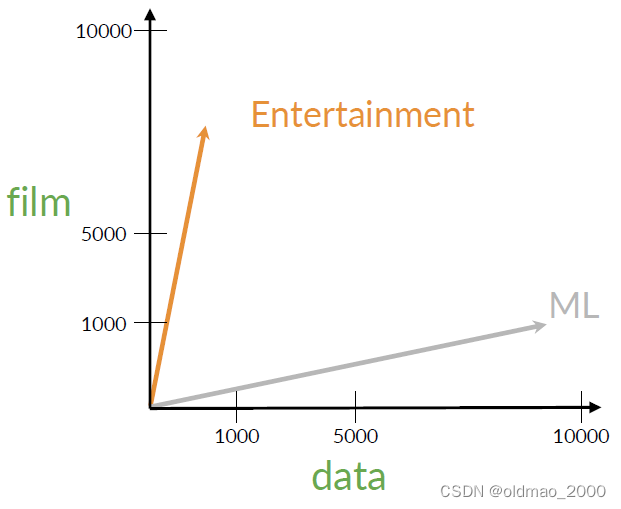
用點表示他們后，可以用歐氏距離很衡量二者的相似度：

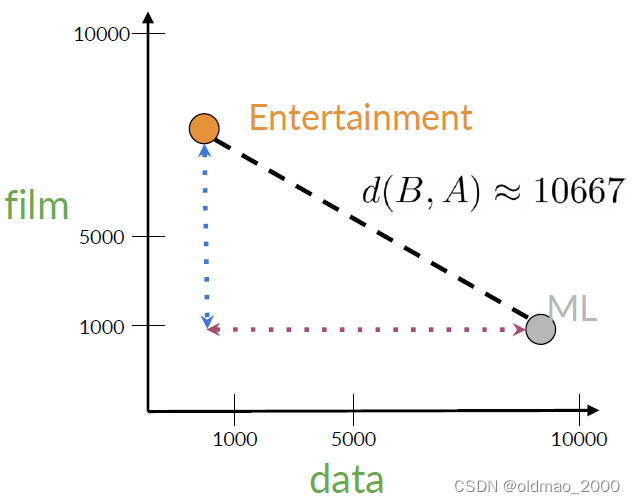
具體公式：
$$d(B,A)=\sqrt{(B_1?A_1{)}^2+(B_2?A_2{)}^2}$$
$B_1?A_1$和$B_2?A_2$分別對應上圖中水平和垂直距離。
本例中帶入數字：
$$d(B,A)=\sqrt{(?8820{)}^2+(6000{)}^2}\approx 10667$$

Euclidean distance for n-dimensional vectors

對于高維向量，歐氏距離仍然適用，例如：

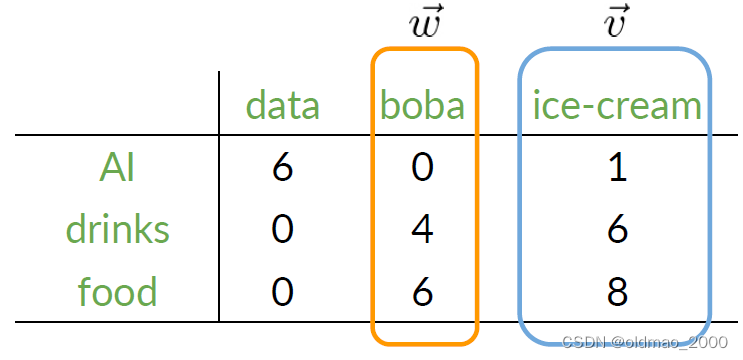
想要計算ice-cream和boba的歐氏距離，則可以使用以下公式：
$$d(\vec{v},\vec{w})=\sqrt{\sum _{i=1}^n(v_i?w_i{)}^2}等價于求范數\text{Norm?of}(\vec{v},\vec{w})$$
ice-cream和boba的歐氏距離可以寫為：
$$\sqrt{(1?0{)}^2+(6?4{)}^2+(8?6{)}^2}=\sqrt{1+4+4}=3$$

Euclidean distance in Python

在這里插入代碼片
# Create numpy vectors v and w
v np. array([1, 6, 8])
w np. array([0, 4, 6])
# Calculate the Euclidean distance d
d = np.linalg.norm(v-w)
# Print the result
print (("The Euclidean distance between v and w is: ", d)

Cosine Similarity: Intuition

先給結論：當語料庫中文章包含單詞數量差異較大時，使用Cosine Similarity
余弦相似度使用文檔之間的角度，因此不依賴于語料庫的大小。

假設我們有eggs和disease兩個單詞在三個語料庫中圖像如下：

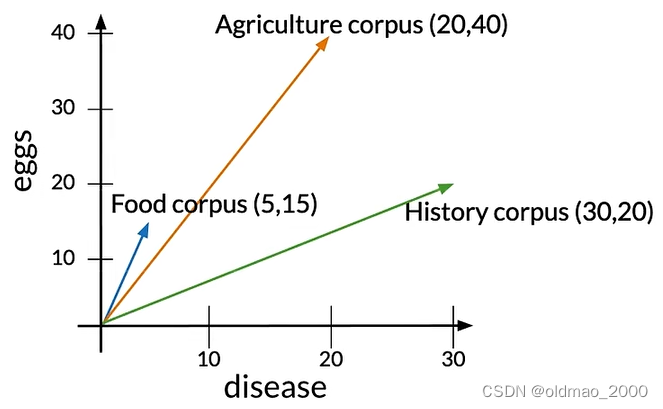
語料庫中各個類型的文章單詞數量不相同，這里的Agriculture和History文章單詞數量基本相同，而Food文章單詞較少。Agriculture與其他兩類文章的歐式距離分別寫為：$d_1$和$d_2$

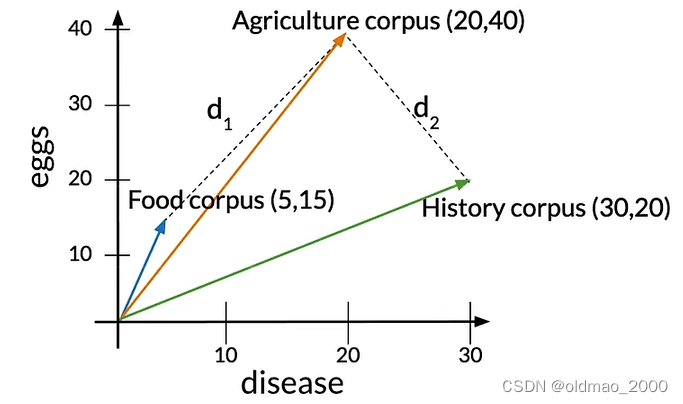
從圖中可以看到$d_2<d_1$，表示Agriculture和History文章相似度更高。
余弦相似度是指The cosine of the angle between the vectors. 當角度接近90度時，余弦接近于0。

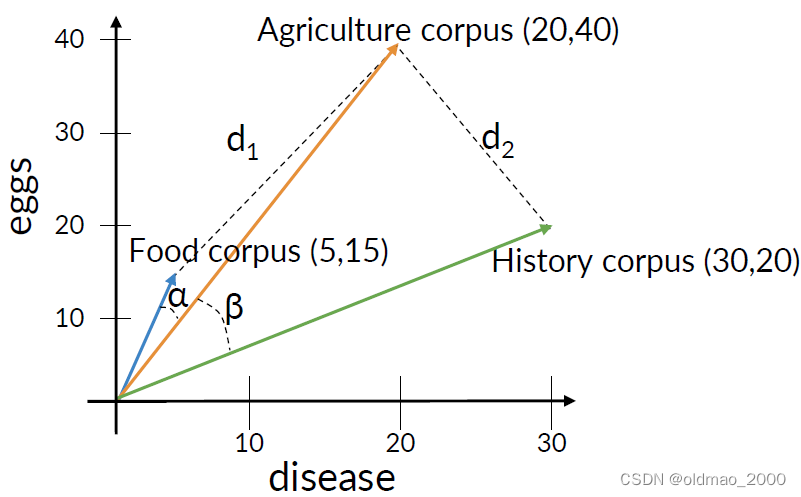
從余弦相似度上看，$\beta >\alpha$，表示Agriculture和Food文章相似度更高。

Cosine Similarity

Previous definitions

先回顧兩個定義：
Vector norm，向量的模（范數）可以表示為：
$$||\vec{v}||=\sqrt{\sum _{i=1}^n{v}_i^2}$$
Dot product點乘可以表示為：
$$\vec{v}?\vec{w}=\sum _{i=1}^n{v}_i?w_i$$

下面是點乘推導：

設有兩個向量$\mathbf{a}$ 和 $\mathbf{b}$，在 $n$維空間中的坐標分別為 $(a_1,a_2,\dots ,a_n)$ 和 $(b_1,b_2,\dots ,b_n)$。這兩個向量的點積定義為：
$$\mathbf{a}?\mathbf{b}=a_1{b}_1+a_2{b}_2+\dots +a_n{b}_n$$

向量 $\mathbf{a}$ 和 $\mathbf{b}$ 的范數（長度）分別是：
$$\Vert \mathbf{a}\Vert =\sqrt{a_1^2+a_2^2+\dots +a_n^2}$$
$$\Vert \mathbf{b}\Vert =\sqrt{b_1^2+b_2^2+\dots +b_n^2}$$

兩個向量之間的夾角 $\theta$ 的余弦值可以通過點積和范數來表示：
$$\cos (\theta )=\frac{\mathbf{a}?\mathbf{b}}{\Vert \mathbf{a}\Vert \Vert \mathbf{b}\Vert }$$

將點積的公式代入上述表達式，我們得到：
$$\cos (\theta )=\frac{a_1{b}_1+a_2{b}_2+\dots +a_n{b}_n}{\sqrt{a_1^2+a_2^2+\dots +a_n^2}\sqrt{b_1^2+b_2^2+\dots +b_n^2}}$$

如果我們將$\cos (\theta )$ 乘以$\mathbf{a}$ 和 $\mathbf{b}$，我們可以得到點積的另一種形式：
$$\Vert \mathbf{a}\Vert \Vert \mathbf{b}\Vert \cos (\theta )=a_1{b}_1+a_2{b}_2+\dots +a_n{b}_n=\mathbf{a}?\mathbf{b}$$

Cosine Similarity

下圖是單詞eggs和disease在語料Agriculture和History出現頻率的可視化表達。

根據上面推導的公式：
$$\begin{gathered} \hat{v}?\hat{w}=||\hat{v}||||\hat{w}||\cos (\beta ) \\ \cos (\beta )=\frac{\hat{v}?\hat{w}}{||\hat{v}||||\hat{w}||} \\ =\frac{(20\times 30)+40\times 20}{\sqrt{20^2+40^2}\times \sqrt{30^2+20^2}}=0.87 \end{gathered}$$
下面是余弦相似度的兩個特殊情形：


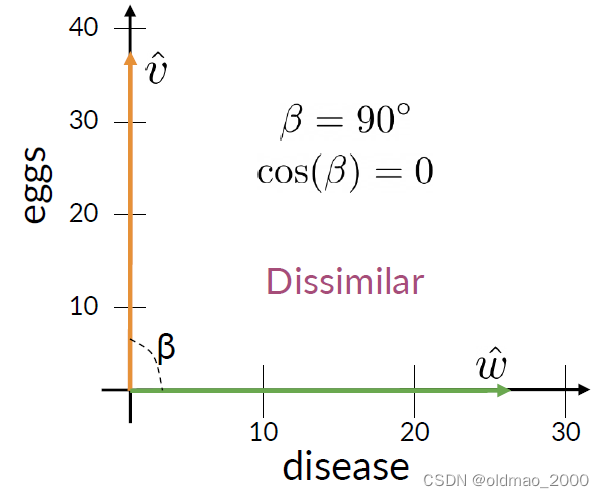
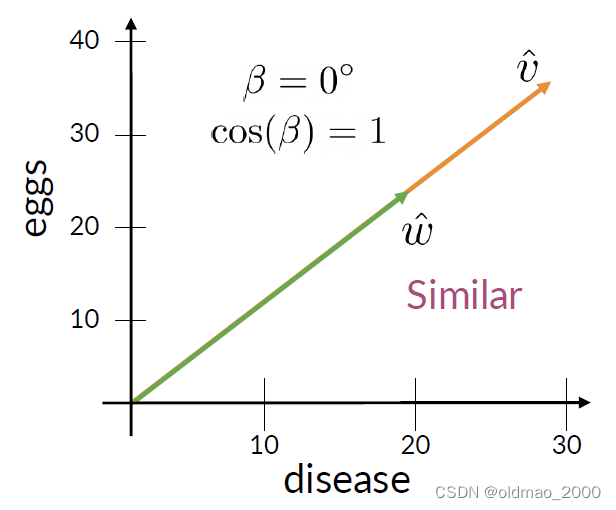
注意：
Cosine Similarity gives values between 0 and 1.

Manipulating Words in Vector Spaces

擴展閱讀：[Mikolov et al, 2013, Distributed Representations of Words and Phrases and their Compositionality]
這里的Manipulating Words，是指對詞向量的加減（平移向量），使得我們可以計算對應關系，例如：已有國家和首都的詞向量空間，已知漂亮國首都是DC（漫威表示不服），求大毛的首都是什么。

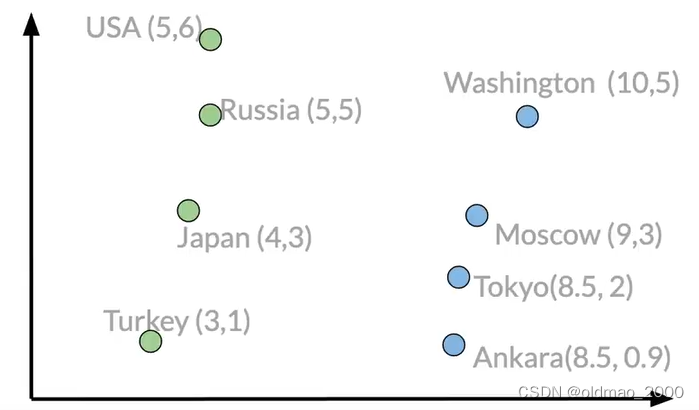
在本例子中，我們有一個假想的二維向量空間，里面包含了不同國家和首都的不同向量表示：

這里我們可以計算USA到Washington的向量差異（也相當于求USA到Washington之間的關系，也就是求連接二者的向量）

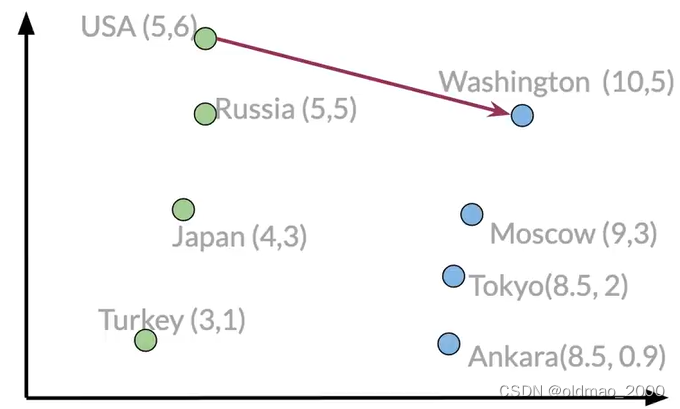
Washington-USA = [5 -1]
通過這個我們就可以知道要找到一個國家的首都需要移動多少距離，對于大毛就有：
Russia + [5 -1]=[10 4]

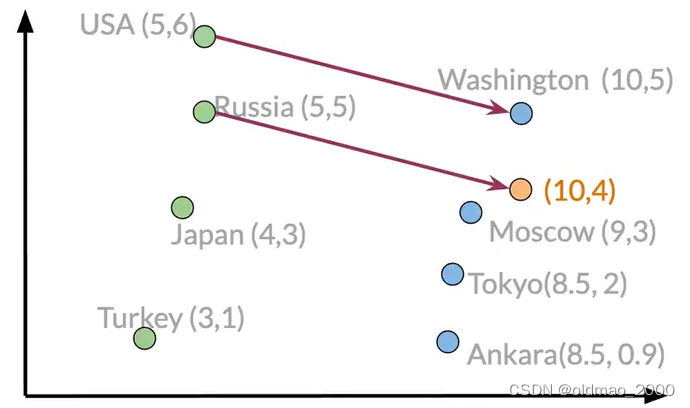
雖然[10 4]沒有匹配到具體的城市，我們可以進一步比較每個城市的歐氏距離或者余弦相似性找到最鄰近的城市。

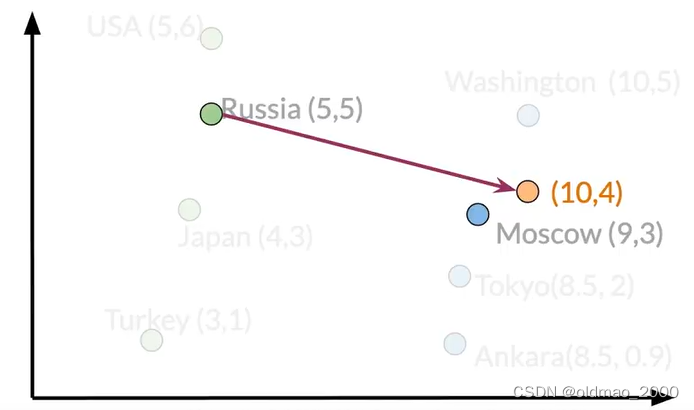
答案是：Moscow

Visualization and PCA

可視化可以讓我們很直觀的看到單詞的相似性，當單詞的向量表示通常是高維的，需要我們將其降維到2D空間便于繪圖，這里先學其中一種降維寫方式：PCA

Visualization of word vectors

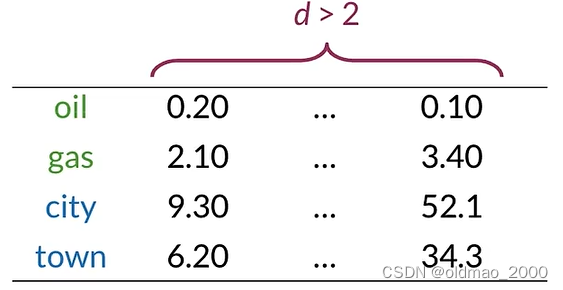
假設詞向量維度遠大于2，已知oil和gas，city和town相似度較高，如何可視化他們之間的關系？答案就是降維：

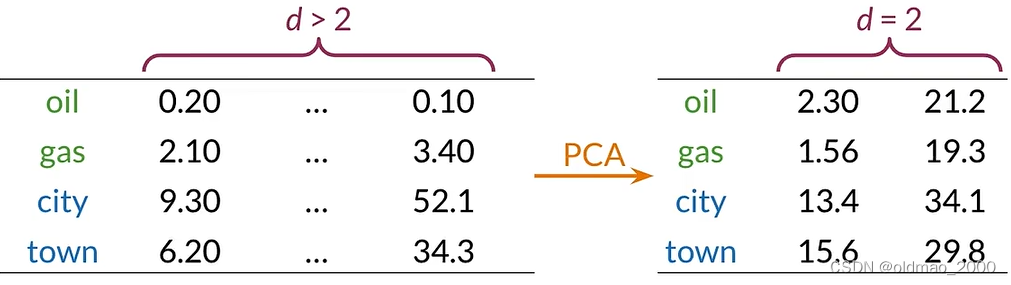
然后再進行可視化，則可得到類似下圖的結果：

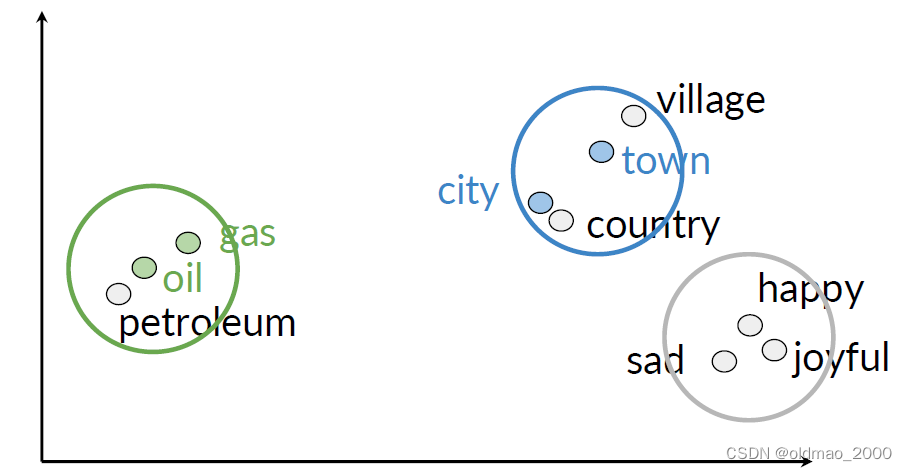
Principal Component Analysis

以二維空間為例來看：

降維就是將Uncorrelated Features映射到另外一個維度空間，并盡量保留更多信息，二維的映射方式一眼就可以看出來，就是垂直映射：

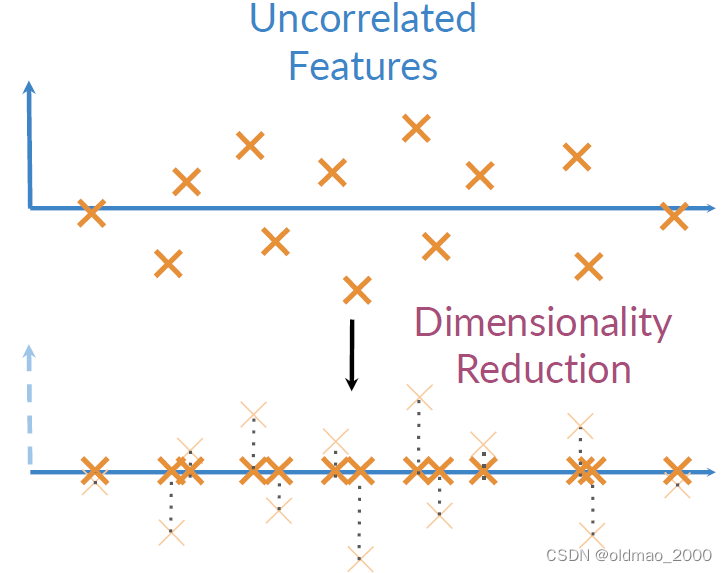
PCA Algorithm

在線代中有兩個概念：Eigenvector（特征向量）和Eigenvalue（特征值）
特征值（Eigenvalue）：
特征值是與線性變換相關聯的一個標量，它描述了在該變換下，一個向量被縮放的比例。
對于一個給定的線性變換（由矩陣表示），如果存在一個非零向量$v$，使得變換后的向量與原向量成比例，即 $Av=\lambda v$，其中 $A$ 是矩陣，$\lambda$ 是一個標量，那么 $\lambda$ 就是 $A$ 的一個特征值，而 $v$ 就是對應的特征向量。
特征向量（Eigenvector）：
特征向量是線性變換下保持方向不變的向量，或者更準確地說，是方向被縮放的向量。
在上述方程 $Av=\lambda v$ 中，如果 $\lambda \ne 0$，那么 $v$ 就是 $A$ 的一個特征向量，它與特征值 $\lambda$ 配對出現。
不需要知道如何計算這兩個東西
算法第一步是為這一步獲取一組無關的特征，需要對數據進行歸一化，然后計算方差矩陣。
$$\text{Mean?Normalize?Data?}{x}_i=\frac{x_i?{\mu }_{x_i}}{{\sigma }_{x_i}}$$
第二步計算方差矩陣（Get Covariance Matrix）：$\Sigma$
第三步奇異值分解（Perform SVD）得到一組三個矩陣：$SVD(\Sigma )$

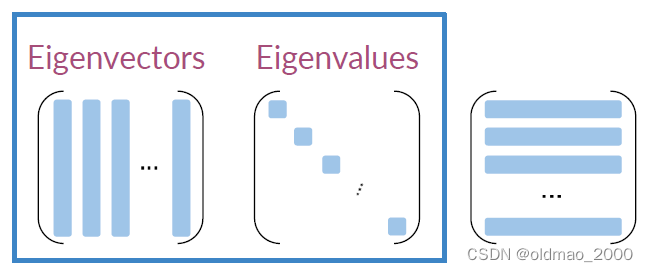
SVD可以直接調用函數解決不用搓輪子。
然后進行投影，將Eigenvector（特征向量）和Eigenvalue（特征值）分別記為$U$和$S$

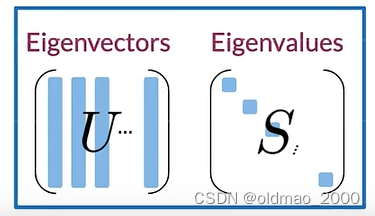
然后通過X點積U的前面兩列來投影數據，這里我們只保留兩列以形成二維可視化空間：

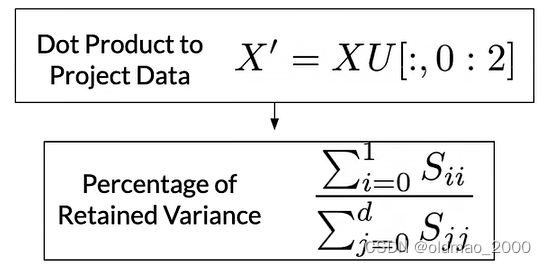
Percentage of Retained Variance: 這表示保留的方差百分比。在PCA中，我們通常選擇前幾個主成分來近似原始數據，這些主成分加起來解釋了原始數據的一定比例的方差。