基于MATLAB對線陣天線進行泰勒加權

相控陣天線——基于MATLAB對線陣進行泰勒加權

前言

一、泰勒綜合

二、單元間距的改變對泰勒陣列方向圖的影響

三、單元數的改變對泰勒陣列激勵分布的影響

四、副瓣電平SLL對泰勒陣列激勵幅度的影響

五、副瓣電平SLL對泰勒陣列方向圖的影響

六、泰勒陣列和切比雪夫陣列的比較

七、副瓣電平和陣元個數間的關系

八、MATLAB代碼

總結

前言

????????前面討論了經典的道爾夫-切比雪夫綜合方法，由此得到的切比雪夫陣列其方向圖是最佳的，即在相同陣列長度情況下對給定的副瓣電平，其主瓣寬度是最窄的，或對給定的主瓣寬度，所得副瓣電平是最低的。但切比雪夫陣列兩端單元的激勵幅度容易發生跳變，不利于饋電。與切比雪夫綜合法密切相關的另外一種經典綜合方法一一泰勒綜合法。采用泰勒綜合法設計的泰勒陣列，其方向圖只是靠近主瓣某個區域內的副瓣電平接近相等，隨后單調地減小。如果設計得當，激勵幅度分布的變化在陣列兩端是單調減的，不會出現兩端單元激勵幅度跳變的情況。本文介紹根據方向圖的副瓣電平對相控陣線陣天線進行泰勒加權（綜合），并通過MATLAB仿真分析泰勒加權方法的優缺點。

提示：以下是本篇文章正文內容，歡迎各位閱讀，轉載請附上鏈接。

一、泰勒綜合

????????采用泰勒綜合法設計的泰勒陣列，其方向圖只是靠近主瓣某個區域內的副瓣電平接近相等，隨后單調地減小，有利于提高天線方向性系數。如果設計得當，激勵幅度分布的變化在陣列兩端是單調減的，不會出現兩端單元激勵幅度跳變的情況。泰勒綜合法設計靈活，適應面寬，在工程設計中得到廣泛應用。

????????對于一個長為L的連續線源，其空間因子(即方向圖函數)可表示為：

$F(u,A)=\cos(\pi\sqrt{u^{2}-A^{2}}) , u=\frac{L}{\lambda}\cos\theta$

此式即為理想的空間因子。根據u的取值可分為主瓣區和副瓣區：

$|u|\leqslant A$ ，為主瓣區： $F(\theta)=\cosh(\pi\sqrt{A^{2}-u^{2}})$

$|u|\geqslant A$ ，為副瓣區： $F(\theta)=\cos(\pi\sqrt{u^{2}-A^{2}})$

? ? ? ? 引入基本函數 $\frac{\sin(\pi u)}{\pi u}$

? ? ? ? 引入波瓣展寬因子 $\sigma$ ，改造理想空間因子：

$F(u,A)=\cos[\pi\sqrt{(u/\sigma)^{2}-A^{2}}],\quad\sigma\geqslant1$

其零點位置為：

???????? $u_{n}=\pm\sigma\sqrt{A^{2}+\left(n-1/2\right)^{2}}\quad,\quad n=1,2,\cdots$

? ? ? ? ?改造基本函數構建泰勒空間因子：

$S(u)=C\frac{\sin(\pi u)}{\pi u}\frac{\prod_{n=1}^{\overline{n}-1}[1-(u/u_{n})^{2}]}{\prod_{n=1}^{\overline{n}-1}[1-(u/n)^{2}]},\quad C=\cosh(\pi A)$

????????該空間因子的含義是:把基本函數的前元 $\overline{n}-1$ 個零點用改造的理想空間因子的零點取代，而第 $\overline{n}$ 個以后的零點保持為基本函數的零點，即

$u_n=\pm\sigma\sqrt{A^{2}+\left(n-1/2\right)^{2}},1\leq n\leq\overline{n}-1$

$u_n=\pm n,n\leq n<\infty$

????????典型的問題是對單元數為N，間距為d的直線陣，采用泰勒綜合法綜合其激勵分布（各單元的激勵電流I），使其陣因子方向圖的副瓣電平為 $-R_{0}$ ?dB。

????????顯然，秦勒綜合時的已知參數是N、d和 $R_{0dB}$ 。泰勒綜合步驟如下:

????????① 計算，其中int表示取整數部分

???????????????? $R_{0}=10^{R_{0dB}/20}$

$A=\frac{1}{\pi}arccoshR_{0}=\frac{1}{\pi}\ln(R_{0}+\sqrt{R_{0}^{2}-1})$

$\overline{n}=int\left(2A^{2}+1/2+1\right)$

$\sigma=\frac{\overline{n}}{\sqrt{A^{2}+\left(\overline{n}-1/2\right)^{2}}}$

????????② 確定單元位置

$z_{n}=\Bigg(n-\frac{N+1}{2}\Bigg)d,n=1,2,\cdots,N$

這樣確定的單元位置對奇、偶數陣列均可，但所得I是從左到右順序排列的。

????????③ 確定變量

$p_{n}=\frac{2\pi}{L}z_{n}, L=Nd$

????????④ 計算各單元的激勵電流

$I_{n}\left(z_{n}\right)=1+2\sum_{m=1}^{\overline{n}-1}\overline{S}\left(m\right)\cos\left(mp_{n}\right), n=1,2,\cdots,N$

其中

$\overline{S}(m)=\begin{cases}1 ,\quad m=0\\\frac{[(\overline{n}-1)!]^2}{(\overline{n}+m-1)!\cdot(\overline{n}-m-1)!}\prod_{n=1}^{\overline{n}-1}\left\{1-\frac{m^2}{\sigma^2[A^2+(n-1/2)^2]}\right\}, 1\leqslant m\leqslant\overline{n}-1\\0 ,\quad m\geqslant\overline{n}\end{cases}$

????????對于泰勒加權可以直接通過以上步驟去綜合，也可以直接使用MATLAB自帶的函數去綜合。這里我們使用MATLAB自帶的函數去綜合。

I=taylorwin(N,n_bar,SLL); %N為陣元數,n_bar是公式中的符號，SLL為副瓣電平,I包含各陣元的激勵幅度

????????仿真參數設置為：

f=2e9; %頻率，單位Hz

N=20; %陣元數

mu=1/2; %陣元間距÷波長

theta0=0;%波束指向角度，單位°

SLL=-30; %副瓣電平，單位dB

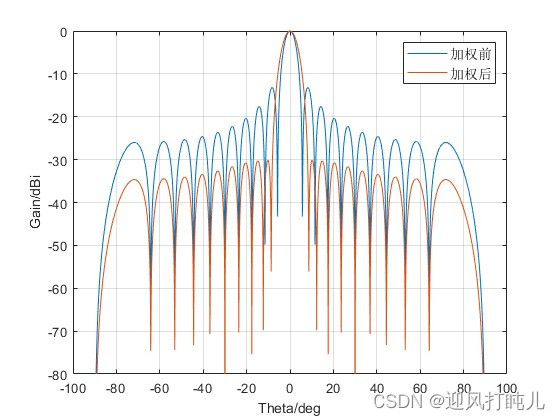
二、單元間距的改變對泰勒陣列方向圖的影響

????????仿真參數設置如下：

f=2e9; %頻率，單位Hz

N=10; %陣元數

theta0=0;%波束指向角度，單位°

SLL=-20; %副瓣電平，單位dB

????????依次設置 $d=\frac{1}{4}\lambda$ ， $d=\frac{1}{2}\lambda$ ， $d=\frac{3}{4}\lambda$ ， $d=\lambda$ ，觀察方向圖及激勵幅度分布。

? ? ? ? 可知，隨著間距的增大，主瓣寬度變窄，副瓣增多，當 $d=\lambda$ 時方向圖出現柵瓣。

三、單元數的改變對泰勒陣列激勵分布的影響

?????????仿真參數設置如下：

f=2e9; %頻率，單位Hz

theta0=0;%波束指向角度，單位°

mu=1/2; %陣元間距÷波長

????????當SLL=-20dB時，依次設置N=15,20,25,30,35，觀察激勵幅度的分布；當SLL=-40dB時，依次設置N=15,20,25,30,35，觀察激勵幅度的分布。

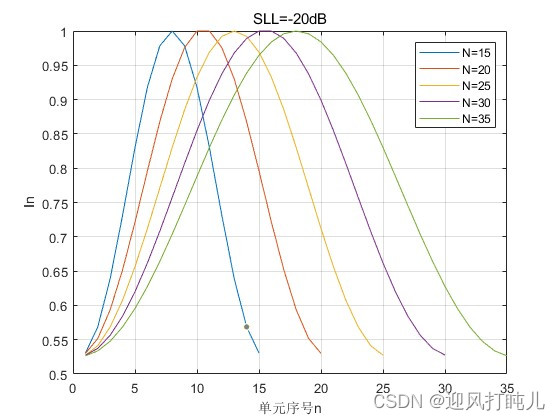
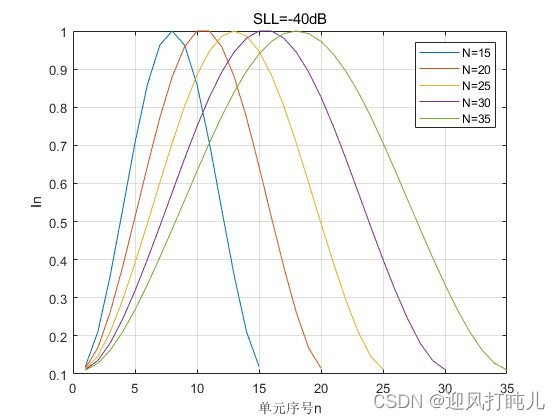
? ? ? ? 可見，泰勒陣列兩端單元的激勵幅度不會像切比雪夫陣列那樣發生跳變。

四、副瓣電平SLL對泰勒陣列激勵幅度的影響

??????????仿真參數設置如下：

f=2e9; %頻率，單位Hz

theta0=0;%波束指向角度，單位°

mu=1/2; %陣元間距÷波長

N=20; %陣元數

????????當N=20時，依次設置SLL=-20,-25,-30,-35,-40dB，觀察激勵幅度的分布。????????

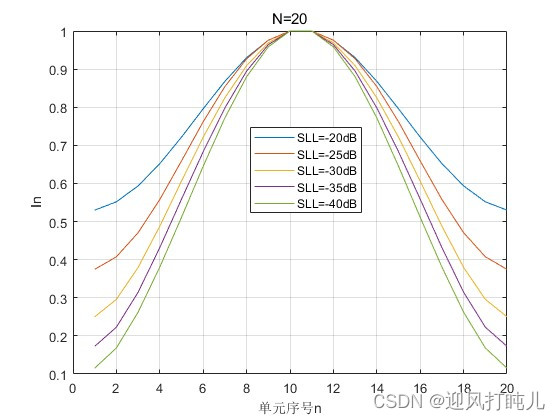
五、副瓣電平SLL對泰勒陣列方向圖的影響

????????仿真參數設置如下：

f=2e9; %頻率，單位Hz

N=16; %陣元數

theta0=20;%波束指向角度，單位°

mu=1/2; %陣元間距÷波長

????????依次設置SLL=-10,-20,-30,-40dB，觀察方向圖。

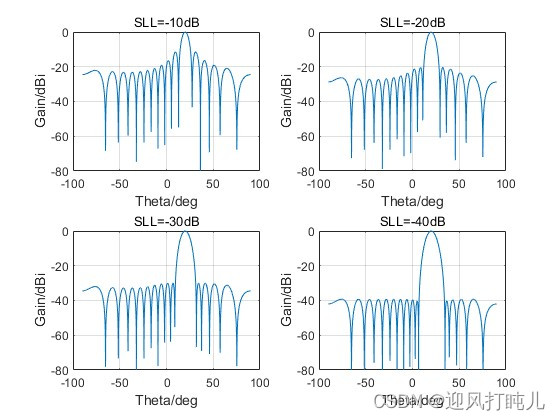
????????由圖可見，單元數N和間距d不變，隨著方向圖副瓣電平的降低，主瓣寬度將略有增大。當副瓣電平比較低時，泰勒陣列和切比雪夫陣列的方向圖比較接近。

六、泰勒陣列和切比雪夫陣列的比較

????????仿真參數設置如下：

f=2e9; %頻率，單位Hz

N=32; %陣元數

theta0=0;%波束指向角度，單位°

mu=1/2; %陣元間距÷波長

SLL=-30; %副瓣電平，單位dB

? ? ? ? 可見，切比雪夫綜合得到的激勵幅度分布在陣列兩端出現了跳變，而泰勒綜合方法所得結果則為單調減少的。切比雪夫綜合方法得到的方向圖為等副瓣電平，而泰勒綜合方法得到的方向圖副瓣電平只有緊靠主瓣的幾個副瓣電平接近相等，其余副瓣電平是遞減的。

????????在相同單元數和單元間距的情況下，泰勒陣列的副瓣越低，則其激勵分布和方向圖就越接近相同情況下的切比雪夫陣列。

七、副瓣電平和陣元個數間的關系

? ? ? ? 一個N單元陣列，當d= $\lambda /2$ 時，其方向圖的零點個數為N-1，主瓣兩側各有副瓣N/2-1個，應有 $N/2-1>\overline{n}$ ，則

???????? $N>2(\overline{n}+1)$

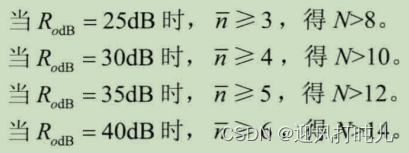
八、MATLAB代碼

https://download.csdn.net/download/m0_66360845/89493202https://download.csdn.net/download/m0_66360845/89493202

總結

????????以上就是今天要分享的全部內容，本文介紹了泰勒加權方法對線陣進行綜合，同時也分析了間距、單元數，副瓣電平等參數對激勵幅度以及方向圖的影響，最后還比較了切比雪夫加權和泰勒加權。

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/web/41134.shtml
繁體地址，請注明出處：http://hk.pswp.cn/web/41134.shtml
英文地址，請注明出處：http://en.pswp.cn/web/41134.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！