太平洋大西洋水流問題

力扣417-太平洋大西洋水流問題

有一個 m × n 的矩形島嶼，與 太平洋 和 大西洋 相鄰。 “太平洋” 處于大陸的左邊界和上邊界，而 “大西洋” 處于大陸的右邊界和下邊界。

這個島被分割成一個由若干方形單元格組成的網格。給定一個 m x n 的整數矩陣 heights ， heights[r] [c] 表示坐標 (r, c) 上單元格 高于海平面的高度 。

島上雨水較多，如果相鄰單元格的高度 小于或等于 當前單元格的高度，雨水可以直接向北、南、東、西流向相鄰單元格。水可以從海洋附近的任何單元格流入海洋。

返回網格坐標 result 的 2D 列表 ，其中 result[i] = [ri, ci] 表示雨水從單元格 (ri, ci) 流動既可流向太平洋也可流向大西洋 。

示例 1：

• 輸入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
• 輸出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]

示例 2：

• 輸入: heights = [[2,1],[1,2]]
• 輸出: [[0,0],[0,1],[1,0],[1,1]]

解題思路

DFS 通過遞歸或棧來實現，沿著一個路徑盡可能深地搜索，直到到達最遠的節點，然后回溯并探索其他路徑。在這個問題中，從每個起始點開始，DFS 沿著四個方向探索，直到無法繼續前進或達到邊界。

class Solution {private final int[][] dir = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}}; // 保存四個方向// 從低向高遍歷，注意這里 visited 是引用，即可以改變傳入的 pacific 和 atlantic 的值private void dfs(int[][] heights, boolean[][] visited, int x, int y) {if (visited[x][y]) return;//如果當前坐標 (x, y) 已經被訪問過，則直接返回，不再進行后續操作。visited[x][y] = true;//只要加入，立刻標記為訪問過的節點for (int[] d : dir) { // 向四個方向遍歷 8-17int nextx = x + d[0];int nexty = y + d[1];// 超過邊界if (nextx < 0 || nextx >= heights.length || nexty < 0 || nexty >= heights[0].length) continue;// 高度不合適，注意這里是從低向高判斷if (heights[x][y] > heights[nextx][nexty]) continue;dfs(heights, visited, nextx, nexty);}}public List<List<Integer>> pacificAtlantic(int[][] heights) {List<List<Integer>> result = new ArrayList<>();int n = heights.length;int m = heights[0].length; // 這里不用擔心空指針，題目要求說了長寬都大于1// 記錄從太平洋邊出發，可以遍歷的節點boolean[][] pacific = new boolean[n][m];// 記錄從大西洋出發，可以遍歷的節點boolean[][] atlantic = new boolean[n][m];// 從最上最下行的節點出發，向高處遍歷for (int i = 0; i < n; i++) {dfs(heights, pacific, i, 0); // 遍歷最左列，接觸太平洋 dfs(heights, atlantic, i, m - 1); // 遍歷最右列，接觸大西洋 }// 從最左最右列的節點出發，向高處遍歷for (int j = 0; j < m; j++) {dfs(heights, pacific, 0, j); // 遍歷最上行，接觸太平洋dfs(heights, atlantic, n - 1, j); // 遍歷最下行，接觸大西洋}// 找到同時被太平洋和大西洋訪問的節點for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (pacific[i][j] && atlantic[i][j]) result.add(List.of(i, j));}}return result;}
}

result.add(List.of(i, j)

List.of()
List.of方法允許我們創建一個不可變的List集合，其中包含指定的元素。
List immutableList = List.of(“apple”, “banana”, “orange”);

Map.of()
Map.of方法允許我們創建一個不可變的Map集合，其中包含指定的鍵值對。
Map<String, Integer> immutableMap = Map.of(“apple”, 1, “banana”, 2, “orange”, 3);

Set.of()
Set.of方法允許我們創建一個不可變的Set集合，其中包含指定的元素。
Set immutableSet = Set.of(“apple”, “banana”, “orange”);

最大人工島

題目描述

力扣827-最大人工島

給你一個大小為 n x n 二進制矩陣 grid 。最多 只能將一格 0 變成 1 。

返回執行此操作后，grid 中最大的島嶼面積是多少？

島嶼 由一組上、下、左、右四個方向相連的 1 形成。

示例 1:

• 輸入: grid = [[1, 0], [0, 1]]
• 輸出: 3
• 解釋: 將一格0變成1，最終連通兩個小島得到面積為 3 的島嶼。

示例 2:

• 輸入: grid = [[1, 1], [1, 0]]
• 輸出: 4
• 解釋: 將一格0變成1，島嶼的面積擴大為 4。

示例 3:

• 輸入: grid = [[1, 1], [1, 1]]
• 輸出: 4
• 解釋: 沒有0可以讓我們變成1，面積依然為 4。

解題思路

其實每次深搜遍歷計算最大島嶼面積，我們都做了很多重復的工作。

只要用一次深搜把每個島嶼的面積記錄下來就好。

第一步：一次遍歷地圖，得出各個島嶼的面積，并做編號記錄。可以使用map記錄，key為島嶼編號，value為島嶼面積 第二步：在遍歷地圖，遍歷0的方格（因為要將0變成1），并統計該1（由0變成的1）周邊島嶼面積，將其相鄰面積相加在一起，遍歷所有 0 之后，就可以得出 選一個0變成1 之后的最大面積。

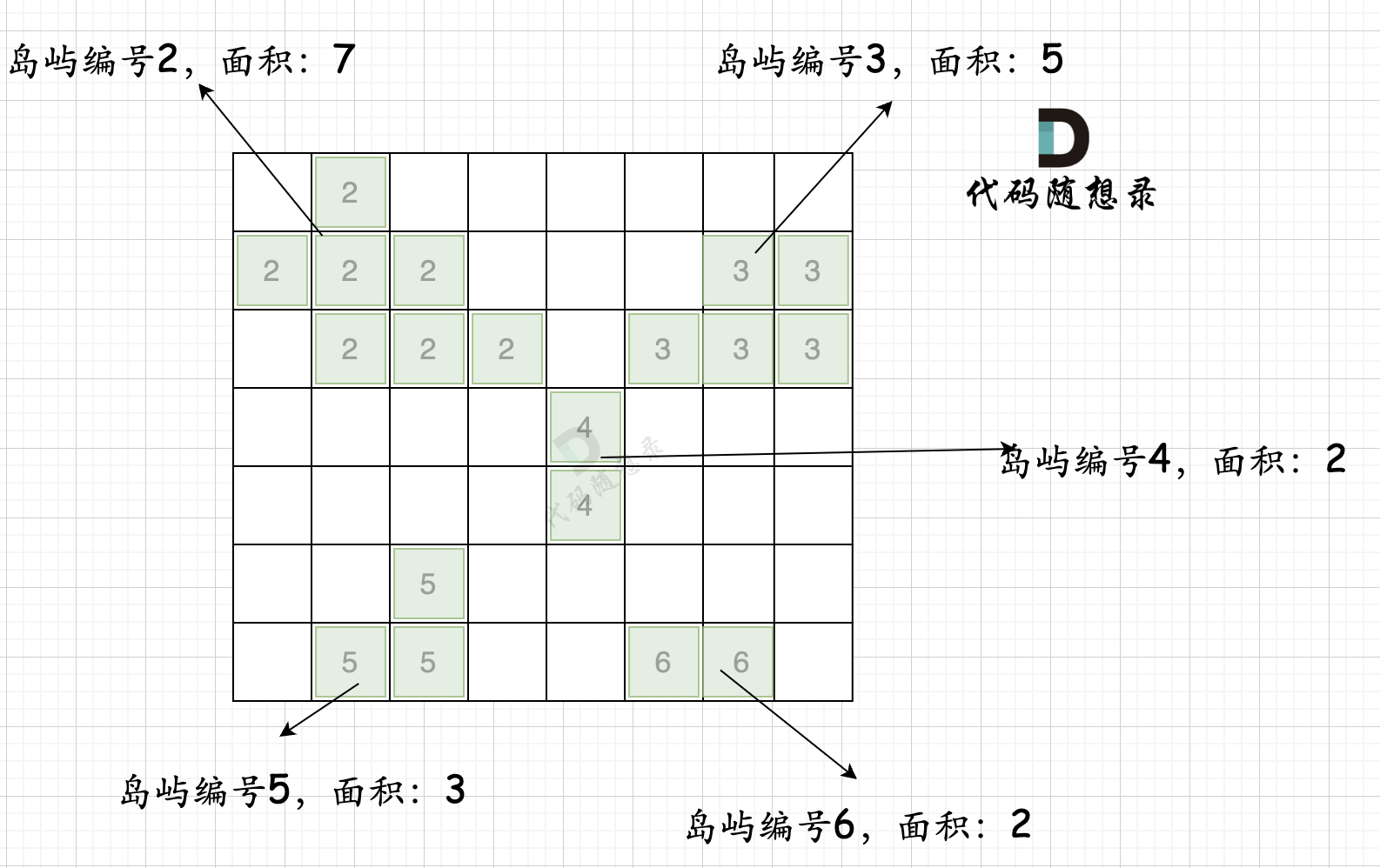
拿如下地圖的島嶼情況來舉例： （1為陸地）

第一步，則遍歷題目，并將島嶼到編號和面積上的統計，過程如圖所示：

本過程代碼如下：

    private int[][] dir = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}}; // 四個方向private void dfs(int[][] grid, boolean[][] visited, int x, int y, int mark) {if (visited[x][y] || grid[x][y] == 0) return; // 終止條件：訪問過的節點 或者 遇到海水visited[x][y] = true; // 標記訪問過grid[x][y] = mark; // 給陸地標記新標簽count++;for (int i = 0; i < 4; i++) {int nextx = x + dir[i][0];int nexty = y + dir[i][1];if (nextx < 0 || nextx >= grid.length || nexty < 0 || nexty >= grid[0].length) continue;  // 越界了，直接跳過dfs(grid, visited, nextx, nexty, mark);}}public int largestIsland(int[][] grid) {int n = grid.length, m = grid[0].length;boolean[][] visited = new boolean[n][m]; // 標記訪問過的點Map<Integer, Integer> gridNum = new HashMap<>();int mark = 2; // 記錄每個島嶼的編號boolean isAllGrid = true; // 標記是否整個地圖都是陸地for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (grid[i][j] == 0) isAllGrid = false;if (!visited[i][j] && grid[i][j] == 1) {count = 0;dfs(grid, visited, i, j, mark); // 將與其鏈接的陸地都標記上 truegridNum.put(mark, count); // 記錄每一個島嶼的面積mark++; // 記錄下一個島嶼編號}}}}

這個過程時間復雜度 n * n 。可能有錄友想：分明是兩個for循環下面套這一個dfs，時間復雜度怎么回事 n * n呢？

其實大家可以仔細看一下代碼，n * n這個方格地圖中，每個節點我們就遍歷一次，并不會重復遍歷。

第二步過程如圖所示：

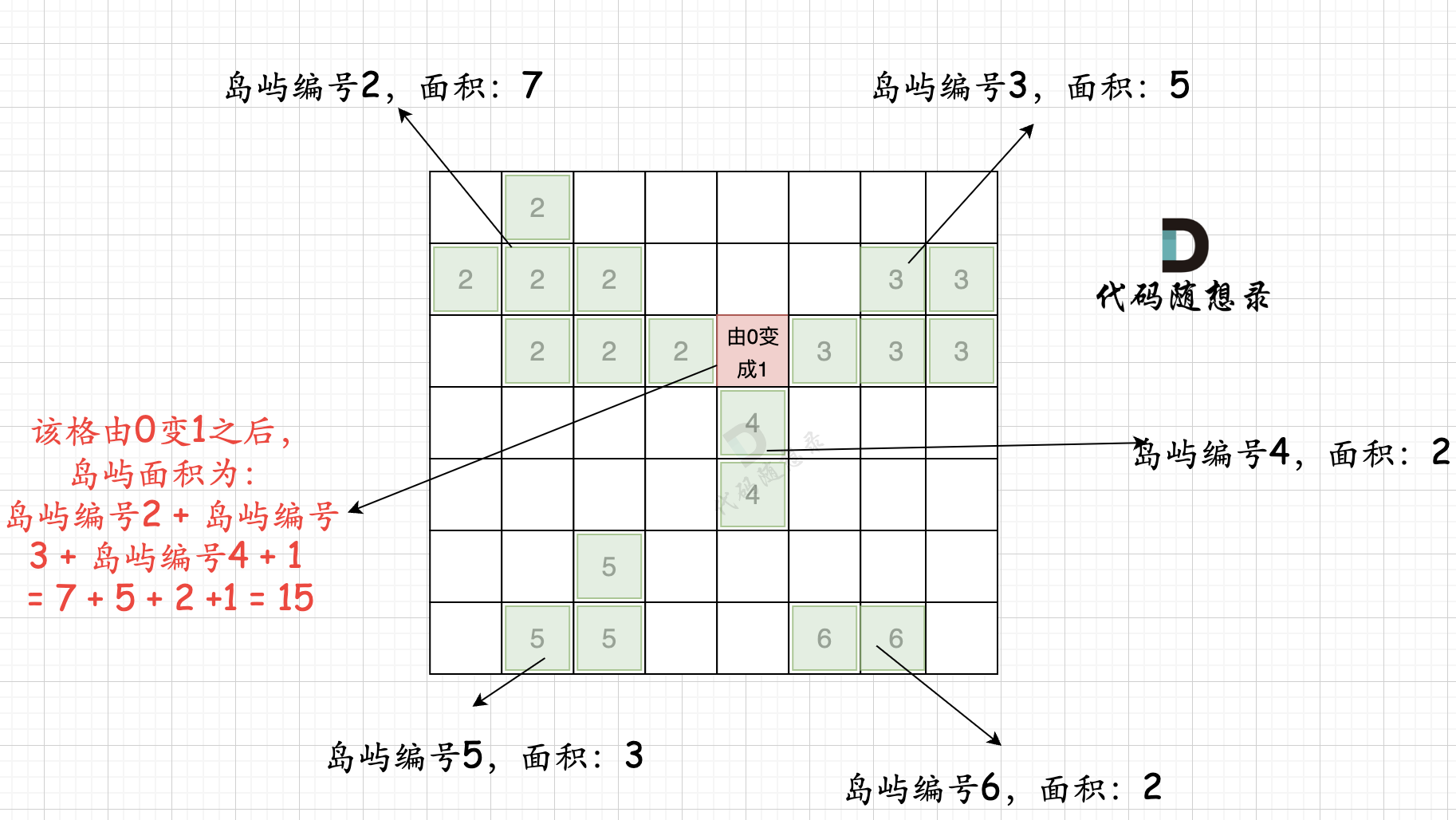
也就是遍歷每一個0的方格，并統計其相鄰島嶼面積，最后取一個最大值。

這個過程的時間復雜度也為 n * n。

所以整個解法的時間復雜度，為 n * n + n * n 也就是 n^2。

當然這里還有一個優化的點，就是 可以不用 visited數組，因為有mark來標記，所以遍歷過的grid[i] [j]是不等于1的。

不過為了讓各個變量各司其事，代碼清晰一些，完整代碼還是使用visited數組來標記。

最后，整體代碼如下：

class Solution {private int count;private int[][] dir = { { 0, 1 }, { 1, 0 }, { -1, 0 }, { 0, -1 } }; // 四個方向private void dfs(int[][] grid, boolean[][] visited, int x, int y, int mark) {if (visited[x][y] || grid[x][y] == 0)return; // 終止條件：訪問過的節點 或者 遇到海水visited[x][y] = true; // 標記訪問過grid[x][y] = mark; // 給陸地標記新標簽count++;for (int i = 0; i < 4; i++) {int nextx = x + dir[i][0];int nexty = y + dir[i][1];if (nextx < 0 || nextx >= grid.length || nexty < 0 || nexty >= grid[0].length)continue; // 越界了，直接跳過dfs(grid, visited, nextx, nexty, mark);}}public int largestIsland(int[][] grid) {int n = grid.length, m = grid[0].length;boolean[][] visited = new boolean[n][m]; // 標記訪問過的點Map<Integer, Integer> gridNum = new HashMap<>();int mark = 2; // 記錄每個島嶼的編號boolean isAllGrid = true; // 標記是否整個地圖都是陸地for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (grid[i][j] == 0)isAllGrid = false;if (!visited[i][j] && grid[i][j] == 1) {count = 0;dfs(grid, visited, i, j, mark); // 將與其鏈接的陸地都標記上 truegridNum.put(mark, count); // 記錄每一個島嶼的面積mark++; // 記錄下一個島嶼編號}}}if (isAllGrid)return n * m; // 如果都是陸地，返回全面積// 以下邏輯是根據添加陸地的位置，計算周邊島嶼面積之和int result = 0; // 記錄最后結果Set<Integer> visitedGrid = new HashSet<>(); // 標記訪問過的島嶼for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {int currentCount = 1; // 記錄連接之后的島嶼數量visitedGrid.clear(); // 每次使用時，清空if (grid[i][j] == 0) {for (int k = 0; k < 4; k++) {int neari = i + dir[k][0]; // 計算相鄰坐標int nearj = j + dir[k][1];if (neari < 0 || neari >= grid.length || nearj < 0 || nearj >= grid[0].length)continue;if (visitedGrid.contains(grid[neari][nearj]))continue; // 添加過的島嶼不要重復添加// 把相鄰四面的島嶼數量加起來if (grid[neari][nearj] > 1) {currentCount += gridNum.get(grid[neari][nearj]);visitedGrid.add(grid[neari][nearj]); // 標記該島嶼已經添加過}}}result = Math.max(result, currentCount);}}return result;}
}