智能優化算法在求解目標函數方面發揮著重要作用，它通過迭代、篩選等方法來尋找目標函數的最優值（極值）。以下是關于智能優化算法求解目標函數的詳細介紹：

一、智能優化算法概述

智能優化算法是一種搜索算法，旨在通過迭代和篩選過程來找到目標函數的最優解。與神經網絡算法不同，智能優化算法不直接利用目標函數的導數信息，而是基于目標函數的值來指導搜索過程。這類算法通常包含多個步驟，如初始化一組解、評估解的性能、選擇解進行迭代等，直到滿足停止條件為止。

二、目標函數在智能優化算法中的作用

目標函數是智能優化算法中用來評估解優劣的關鍵指標，它定義了問題的優化目標，即最大化或最小化的量。目標函數的選擇對算法的性能和效果具有重要影響。一個好的目標函數應能夠準確地反映問題的特性，并提供充分的信息用于指導算法。

三、智能優化算法求解目標函數的過程

1. 初始化：給定一組初始解，這些解是算法搜索的起點。
2. 評估：根據目標函數對當前這組解的性能進行評估，通常是將解代入目標函數并計算其值。
3. 選擇：從當前這組解中選擇一定數量的解作為迭代后的解的基礎。選擇的依據可以是目標函數的值或其他啟發式信息。
4. 迭代：對選定的解進行操作（如變異、交叉等），得到新的解。然后重新評估這些新解的性能，并重復上述步驟進行迭代。
5. 停止條件：當滿足一定的條件（如達到最大迭代次數、找到滿足要求的解等）時，算法停止搜索并輸出最優解。

四、智能優化算法的特點

1. 全局搜索能力：智能優化算法通常具有全局搜索能力，能夠在較大的解空間中尋找最優解。
2. 魯棒性：這類算法對初始解的選擇不敏感，能夠在不同的初始條件下找到較優的解。
3. 易于實現：智能優化算法通常具有簡單的實現方式，易于編程實現和調試。

五、智能優化算法的應用實例

智能優化算法在多個領域都有廣泛的應用，如機器學習、圖像處理、路徑規劃等。以路徑規劃為例，智能優化算法可以用于求解旅行商問題（TSP）、車輛路徑問題（VRP）等，通過尋找最優的路徑來降低運輸成本或提高運輸效率。

六、總結

智能優化算法通過迭代和篩選過程來求解目標函數的最優解，具有全局搜索能力和魯棒性。在實際應用中，應根據具體問題的特點選擇合適的目標函數和智能優化算法，以提高求解效率和效果。

求解下列函數：

代碼實現

定義目標函數：

Get_Functions_details?函數的主要目的是為給定的優化函數?F（通過其標識符字符串表示）提供相關的參數設置，包括：

• lb（lower bound）：優化變量的下界，通常是一個與問題維度?dim?相同長度的向量。
• ub（upper bound）：優化變量的上界，也是一個與?dim?相同長度的向量。
• dim（dimension）：問題的維度，即優化變量的數量。
• fobj（function object）：優化函數的句柄，指向實際計算目標函數值的函數。

function [lb,ub,dim,fobj] = Get_Functions_details(F)switch Fcase 'F1'fobj = @F1;lb=-100;ub=100;dim=30;case 'F2'fobj = @F2;lb=-10;ub=10;dim=30;case 'F3'fobj = @F3;lb=-100;ub=100;dim=30;case 'F4'fobj = @F4;lb=-1.28;ub=1.28;dim=30;case 'F5'fobj = @F5;lb=-100;ub=100;dim=30;case 'F6'fobj = @F6;lb=-10;ub=10;dim=30;end% F1function o = F1(x)
o=sum(x.^2);
end% F2function o= F2(x)
% dim=size(x,2);
for i=1:dimo=sum(i.*(x.^2));
end
end% F3
function o = F3(x)
o=sum(abs((x+.5)).^2);
end% F4function o = F4(x)
dim=size(x,2);
o=sum(1:dim.*(x.^4))+rand;
end% F5function o = F5(x)
o=-cos(x(1))*cos(x(2))*exp(-(x(1)-pi)^2-(x(2)-pi)^2);
end% F6function o = F6(x)
o=0.26*((x(1)^2)+(x(2)^2))-0.48*(x(1)*(x(2)));
endend

initialization.m?

初始化：處理所有變量具有相同邊界范圍的情況，也可以處理每個變量具有不同邊界范圍的情況。通過隨機初始化，它確保了搜索算法的起點是隨機且均勻的分布在問題空間內的。

% This function initialize the first population of search radiations (Agents)
function Positions=initialization(SearchAgents_no,dim,ub,lb)Boundary_no= size(ub,2); % numnber of boundaries% If the boundaries of all variables are equal and user enter a signle
% number for both ub and lb
if Boundary_no==1Positions=rand(SearchAgents_no,dim).*(ub-lb)+lb;
end% If each variable has a different lb and ub
if Boundary_no>1for i=1:dimub_i=ub(i);lb_i=lb(i);Positions(:,i)=rand(SearchAgents_no,1).*(ub_i-lb_i)+lb_i;end
end

main.m

clc
clear
close all
%%
Fun_name='F1'; 
SearchAgents_no=30;                     
Max_iterations=5000;                 
[lb,ub,dim,fobj]=Get_Functions_details(Fun_name); % Object function information
%%% 算法 WOA
[Best_score,Best_pos,WOA_cg_curve]=WOA(SearchAgents_no,Max_iterations,lb,ub,dim,fobj);
% 算法 PSO
[Best_score1,Best_pos1,PSO_cg_curve]=PSO(SearchAgents_no,Max_iterations,lb,ub,dim,fobj);
% 算法DBO
[Best_score2,Best_pos2,DBO_cg_curve]=DBO(SearchAgents_no,Max_iterations,lb,ub,dim,fobj);display(['The best solution obtained by WOA is  ', num2str(Best_pos)]);
display(['The best optimal value of the objective function found by WOA is  ', num2str(Best_score)]);display(['The best solution obtained by PSO is  ', num2str(Best_pos1)]);
display(['The best optimal value of the objective function found by PSO is  ', num2str(Best_score1)]);display(['The best solution obtained by DBO is  ', num2str(Best_pos2)]);
display(['The best optimal value of the objective function found by DBO is  ', num2str(Best_score2)]);CNT=40;
k=round(linspace(1,Max_iterations,CNT)); 
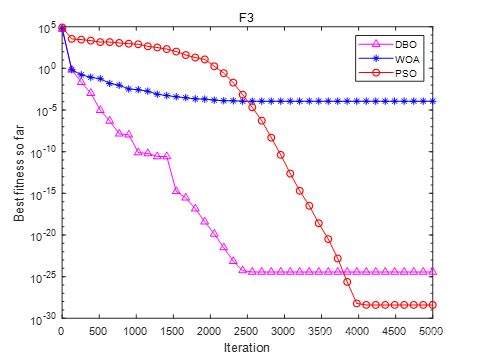
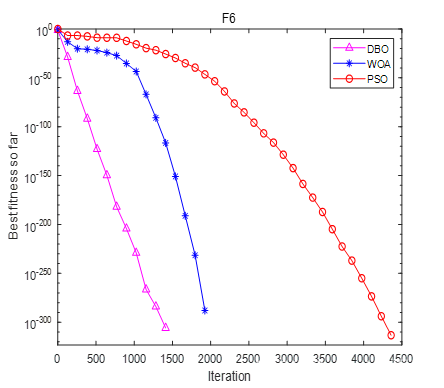
iter=1:1:Max_iterations;h1 = semilogy(iter(k),DBO_cg_curve(k),'m-^','linewidth',1);
hold on
h2 = semilogy(iter(k),WOA_cg_curve(k),'b-*','linewidth',1);
hold on
h3 = semilogy(iter(k),PSO_cg_curve(k),'r-o','linewidth',1);
title(Fun_name)
xlabel('Iteration');
ylabel('Best fitness so far');
legend('DBO','WOA','PSO');