前言
思路及算法思維,指路 代碼隨想錄。
題目來自 LeetCode。
day 55,又是一個周一,不能再堅持~
題目詳情
[42] 接雨水
題目描述
42 接雨水

解題思路
前提:雨水形成的情況是凹的, 需要前中后3個元素,計算該元素左右兩側的第一個大于該高度的高度
思路:單調遞增棧
重點:單調棧的思維
代碼實現
C語言
單調遞增棧
單調遞增棧: 【橫向計算形成凹行柱體的雨水】
雨水形成的情況是凹的, 需要當前新的棧頂元素, 計算的是舊的棧頂元素形成的雨水
// 單調遞增棧: 雨水形成的情況是凹的, 需要當前新的棧頂元素, 計算的是舊的棧頂元素形成的雨水int minFun(int p1, int p2)
{return p1 < p2 ? p1 : p2;
}int trap(int* height, int heightSize) {int stack[heightSize];int top = 0;// 遍歷計算每個柱子接到的雨水之和int sum = 0;for (int i = 0; i < heightSize; i++) {// 單調遞增棧// 當前元素比棧頂元素大,不滿足單調遞增棧的要求while (top > 0 && height[i] > height[stack[top - 1]]) {// 彈出當前棧頂元素int midIndex = stack[top - 1];top--;// 雨水形成的情況是凹的, 需要當前新的棧頂元素, 計算的是舊的棧頂元素形成的雨水if (top > 0) {int leftIndex = stack[top - 1];sum += (minFun(height[leftIndex], height[i]) - height[midIndex]) * (i - leftIndex - 1);}}stack[top] = i;top++;}return sum;
}
雙指針
雙指針解法:【豎向計算每個柱體形成的雨水】
兩次遍歷求當前左側最高柱子高度maxLeft[i]和右側最高柱子高度maxRight[i]
// 雙指針解法:兩次遍歷求當前左側最高柱子高度maxLeft[i]和右側最高柱子高度maxRight[i]int maxFun(int p1, int p2)
{return p1 > p2 ? p1 : p2;
}int minFun(int p1, int p2)
{return p1 < p2 ? p1 : p2;
}int trap(int* height, int heightSize) {int maxLeft[heightSize];int maxRight[heightSize];// 遍歷搜索左側最高柱子高度maxLeft[0] = height[0];for (int i = 1; i < heightSize; i++) {maxLeft[i] = maxFun(height[i], maxLeft[i - 1]);}// 遍歷搜索右側最高柱子高度maxRight[heightSize - 1] = height[heightSize - 1];for (int j = heightSize - 2; j >= 0; j--) {maxRight[j] = maxFun(height[j], maxRight[j + 1]);}// 遍歷計算每個柱子接到的雨水之和int sum = 0;for (int k = 0; k < heightSize; k++) {sum += minFun(maxLeft[k], maxRight[k]) - height[k];}return sum;
}
[84] 柱狀圖中最大的矩形
題目描述
84 柱狀圖中最大的矩形
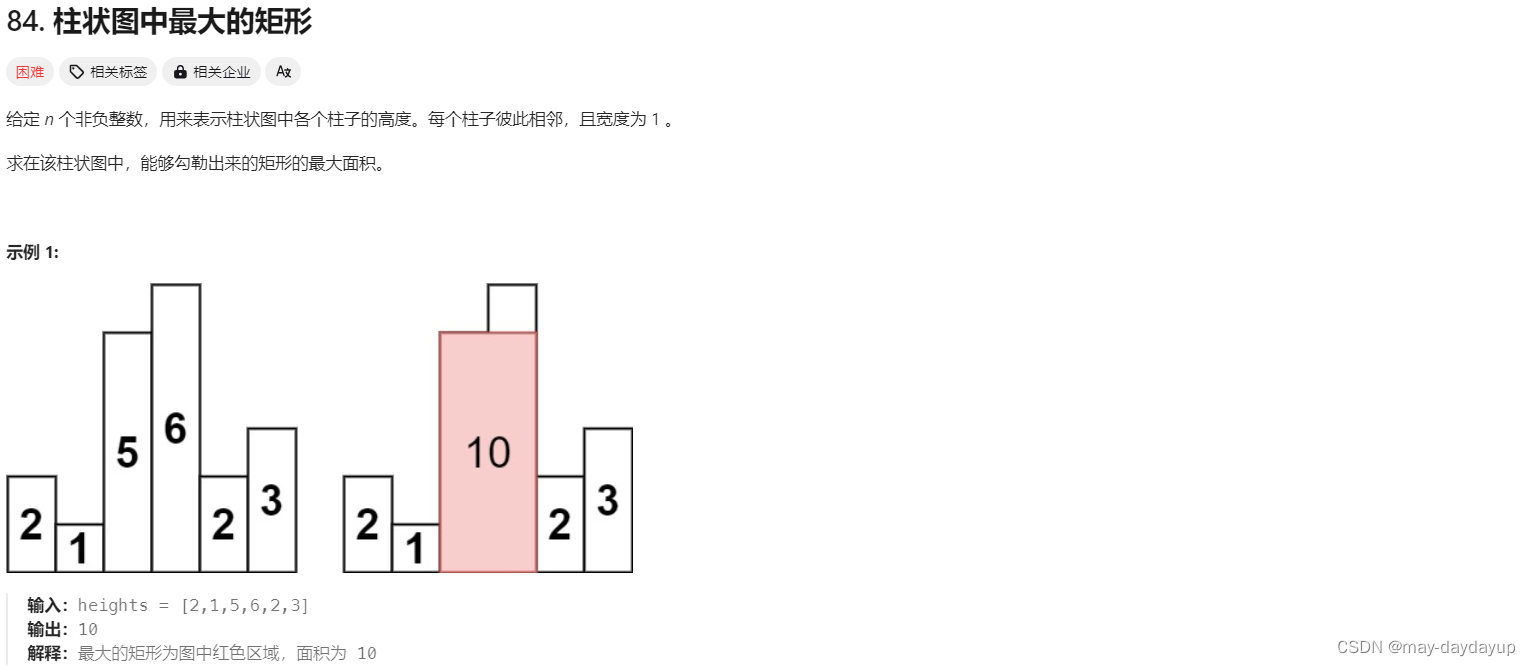
解題思路
前提:柱狀圖形成的最大面積,需要求解該柱子左右兩側 最遠>=該柱子高度的柱子寬度,即可以求解該柱子左右兩側小于該柱子高度的位置,進而計算所求寬度
思路:單調遞減棧
重點:單調棧的思維
代碼實現
C語言
單調遞減棧
// 單調遞減棧: 尋找該柱子左右兩側第一個小于該柱子高度的柱子, 即可找到最后左右兩側最遠一個大于該柱子高度的連續柱子, 計算所形成的的最大面積
// 棧頂到棧底,元素依次遞減int minFun(int p1, int p2)
{return p1 < p2 ? p1 : p2;
}int maxFun(int p1, int p2)
{return p1 > p2 ? p1 : p2;
}int largestRectangleArea(int* heights, int heightsSize) {int stack[heightsSize];int top = 0;int maxSum = 0;// 遍歷for (int i = 0; i < heightsSize; i++) {// 尋找查找棧頂柱子的右側第一個低于棧頂柱子的柱子位置while (top > 0 && heights[i] < heights[stack[top - 1]]) {// 彈出棧頂元素int midIndex = stack[top - 1];top--;// 計算彈出元素所形成的凸型的面積// 判斷是否形成凸的最左側int leftIndex = 0;if (top > 0) {leftIndex = stack[top - 1] + 1;}int rightIndex = i - 1;int sum = heights[midIndex] * (rightIndex - leftIndex + 1);maxSum = maxFun(maxSum, sum);}stack[top] = i;top++;}// 判斷是否最后沒有形成凸的最右側,清空棧while (top > 0){int midIndex = stack[top - 1];top--;if (top == 0) {// 此時這個元素為當前元素數組中最小的元素int sum = heights[midIndex] * heightsSize;maxSum = maxFun(maxSum, sum);} else {// 此時單調棧中元素遞減int sum = heights[midIndex] * ((heightsSize - 1) - (stack[top - 1] + 1) + 1);maxSum = maxFun(maxSum, sum);}}return maxSum;
}
針對數組單調遞增等不能形成凸型的特殊情況, 需要特殊處理,
所以在原數組首尾添加最小元素0, 以便對原數組做同一處理。
優化代碼如下。
// 單調遞減棧: 尋找該柱子左右兩側第一個小于該柱子高度的柱子, 即可找到最后左右兩側最遠一個大于該柱子高度的連續柱子, 計算所形成的的最大面積
// 棧頂到棧底,元素依次遞減
// 針對數組單調遞增等的特殊情況, 需要特殊處理,所以在原數組首尾添加最小元素0,以便對原數組做同一處理int maxFun(int p1, int p2)
{return p1 > p2 ? p1 : p2;
}int largestRectangleArea(int* heights, int heightsSize) {int newHeightsSize = heightsSize + 2;int newHeights[newHeightsSize];newHeights[0] = 0;newHeights[newHeightsSize - 1] = 0;for (int t = 1; t < newHeightsSize - 1; t++) {newHeights[t] = heights[t - 1];}int stack[newHeightsSize];int top = 0;int maxSum = 0;// 遍歷for (int i = 0; i < newHeightsSize; i++) {// 尋找查找棧頂柱子的右側第一個低于棧頂柱子的柱子位置// 當遍歷到新數組的最后一個元素0, 必可以進入該循環進行處理while (top > 0 && newHeights[i] < newHeights[stack[top - 1]]) {// 彈出棧頂元素int midIndex = stack[top - 1];top--;// 計算彈出元素所形成的凹型的面積// 此處的棧中必有新數組的首元素0int leftIndex = stack[top - 1] + 1;int rightIndex = i - 1;int sum = newHeights[midIndex] * (rightIndex - leftIndex + 1);maxSum = maxFun(maxSum, sum);}stack[top] = i;top++;}return maxSum;
}
雙指針
尋找該柱子左側的第一個小于該柱子的高度的下標minLeftIndex[i] 和 右側第一個小于該柱子的高度的下標minRightIndex[i],
進而計算不小于該柱子高度的連續長度。
// 雙指針方法: 尋找該柱子左側的第一個小于該柱子的高度的下標minLeftIndex[i] 和 右側第一個小于該柱子的高度的下標minRightIndex[i]
// 計算以當前柱子形成凹形狀的柱子的最大面積int minFun(int p1, int p2)
{return p1 < p2 ? p1 : p2;
}int maxFun(int p1, int p2)
{return p1 > p2 ? p1 : p2;
}int largestRectangleArea(int* heights, int heightsSize) {int minLeftIndex[heightsSize];int minRightIndex[heightsSize];// 遍歷,尋找該柱子左側的第一個小于該柱子的高度的下標minLeftIndex[0] = -1;for (int i = 1; i < heightsSize; i++) {int t = i - 1;// 查找左側第一個小于該柱子高度的柱子下標while (t >= 0 && heights[t] >= heights[i]) {t = minLeftIndex[t];}minLeftIndex[i] = t;}// 遍歷,尋找該柱子右側的第一個小于該柱子的高度的下標minRightIndex[heightsSize - 1] = heightsSize;for (int j = heightsSize - 2; j >= 0; j--) {int t = j + 1;// 查找右側第一個小于該柱子高度的柱子下標while (t < heightsSize && heights[t] >= heights[j]) {t = minRightIndex[t];}minRightIndex[j] = t;}// 遍歷尋找最大面積int sum = 0;int maxSum = 0;for (int k = 0; k < heightsSize; k++) {// 求以當前柱子形成凹形狀的柱子的最大面積int leftIndex = minLeftIndex[k] + 1;int rightIndex = minRightIndex[k] - 1;sum = heights[k] * (rightIndex - leftIndex + 1);maxSum = maxFun(maxSum, sum);}return maxSum;
}
今日收獲
- 單調棧,以及為了使用單調棧所做的變化



















