目錄

Regression for Dummies

Conditionally Random Experiments

Dummy Variables

---

Regression for Dummies

回歸和正交化固然很好，但歸根結底，你必須做出獨立性假設。你必須假設，在考慮到某些協變量的情況下，干預看起來與隨機分配一樣好。這可能相當困難。很難知道模型中是否包含了所有的混雜因素。因此，盡可能推動隨機實驗是非常有意義的。例如，在銀行業的例子中，如果信用額度是隨機的就好了，因為這樣就可以很直接地估算出信用額度對違約率和客戶消費的影響。問題是，這個實驗的成本將高得驚人。你將會給風險極高的客戶提供隨機信用額度，而這些客戶很可能會違約并造成巨大損失。

Conditionally Random Experiments

解決這一難題的方法并不是理想的隨機對照試驗，但卻是最理想的方法：分層或有條件隨機試驗。在這種實驗中，實驗線不是完全隨機的，而是從相同的概率分布中抽取的，因此您需要創建多個局部實驗，根據客戶的協變量從不同的分布中抽取樣本。例如，您知道變量 credit_score1 是客戶風險的代理變量。因此，您可以用它來創建風險較高或較低的客戶群體，將他們劃分為信用分數 1 相似的桶。然后，對于高風險組（信用分數低），您可以從平均分較低的分布中隨機抽取信用額度；對于低風險客戶（信用分數高），您可以從平均分較高的分布中隨機抽取信用額度：

 risk_data_rnd = pd.read_csv("./data/risk_data_rnd.csv")risk_data_rnd.head()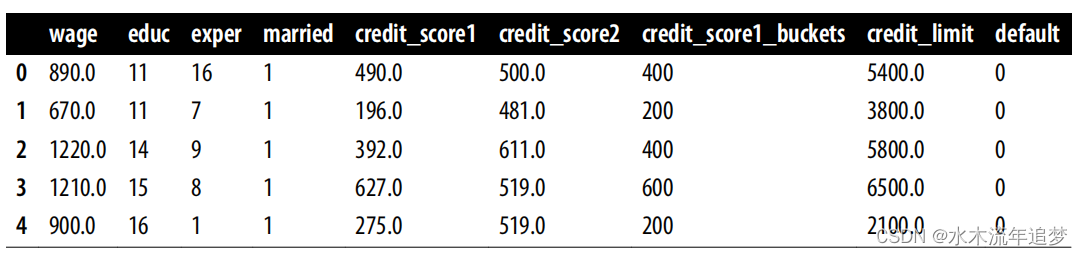

繪制按credit_score1_buckets劃分的信用額度直方圖，可以看到各行的取樣分布不同。得分較高的組別--低風險客戶--的直方圖向左傾斜，線條較長。風險較高的客戶組--低分--的貸款額度分布圖向右傾斜，貸款額度較低。這種實驗探索的信貸額度與最佳額度相差不大，從而降低了測試成本，使其更易于管理：

這并不意味著條件隨機實驗比完全隨機實驗更好。出于這個原因，如果您選擇條件隨機實驗，無論出于什么原因，都要盡量使其接近完全隨機實驗。這意味著

• - 組數越少，處理條件隨機測試就越容易。在本例中，您只有 5 個組，因為您把 credit_score1 分成了 200 個桶，分數從 0 到 1,000。將不同的組與不同的干預分布結合起來會增加復雜性，因此堅持少分組是個好主意。
• - 各組間干預分布的重疊越大，你的實驗就越輕松。這與陽性假設有關。在這個例子中，如果高風險組獲得高線的概率為零，那么您就必須依靠危險的推斷才能知道如果他們獲得高線會發生什么。

如果把這兩條經驗法則調到最大值，就會得到一個完全隨機的實驗，這意味著這兩條經驗法則都需要權衡：組數越少，重疊度越高，實驗就越容易讀取，但成本也越高，反之亦然。

Dummy Variables

條件隨機實驗的好處在于，條件獨立性假設更加可信，因為你知道在你選擇的分類變量下，各條線是隨機分配的。其缺點是，簡單地將結果與被處理者進行回歸，會產生有偏差的估計值。例如，以下是在不包含混雜因素的情況下估計模型的結果：

 model = smf.ols("default ~ credit_limit", data=risk_data_rnd).fit()model.summary().tables[1]

如圖所示，因果參數 β1 的估計值為負值，這在這里是沒有意義的。較高的信用額度可能并不會降低客戶的風險。實際情況是，在這個數據中，由于實驗的設計方式，風險較低的客戶--credit_score1 高的客戶--平均獲得了更高的額度。

為了對此進行調整，需要在模型中加入隨機分配干預的組別。在這種情況下，需要credit_score1_buckets. 進行控制。盡管該組用數字表示，但它實際上是一個分類變量：它代表一個組。因此，控制組本身的方法是創建啞變量。虛擬變量是一個群體的二進制列。如果客戶屬于該組，則為 1，否則為 0。由于一個客戶只能來自一個組，因此最多只有一列虛擬變量為 1，其他列均為 0。如果您有機器學習背景，您可能會知道這是one-hot。它們完全是一回事。

在 pandas 中，你可以使用 pd.get_dummies 函數來創建啞列。在這里，我傳遞了表示組的列 credit_score1_buckets，并表示我想要創建后綴為 sb（表示分數桶）的啞列。此外，我還刪除了第一個虛擬列，即 0 到 200 分桶的虛擬列。這是因為其中一列是多余的。如果我知道所有其他列都是 0，那么我放棄的那一列 一定是 1：

 risk_data_dummies = (
risk_data_rnd.join(pd.get_dummies(risk_data_rnd["credit_score1_buckets"],prefix="sb",drop_first=True))
)

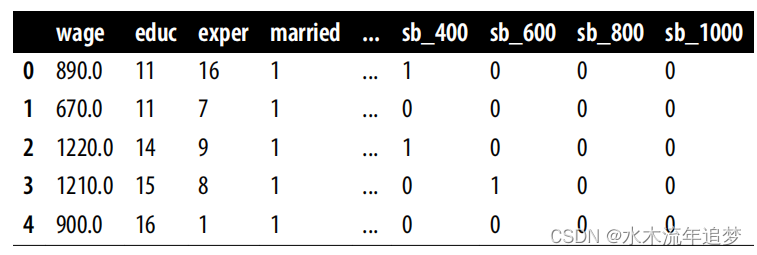一旦您有了虛擬列，您就可以將它們添加到您的模型中，并再次估計β1：

現在，你會得到一個更合理的估計，這至少是積極的，這表明更多的信用額度會增加違約風險。

 model = smf.ols("default ~ credit_limit + sb_200+sb_400+sb_600+sb_800+sb_1000",data=risk_data_dummies).fit()model.summary().tables[1]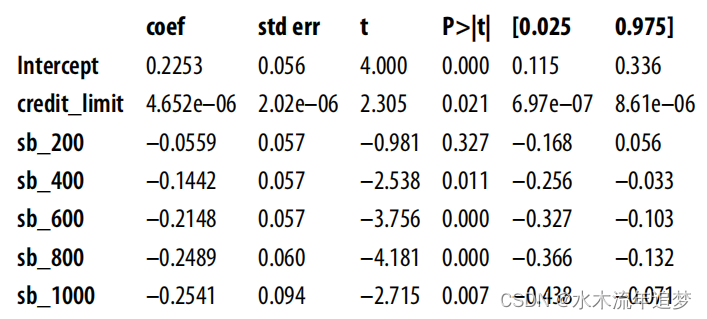

 model = smf.ols("default ~ credit_limit + C(credit_score1_buckets)",data=risk_data_rnd).fit()model.summary().tables[1]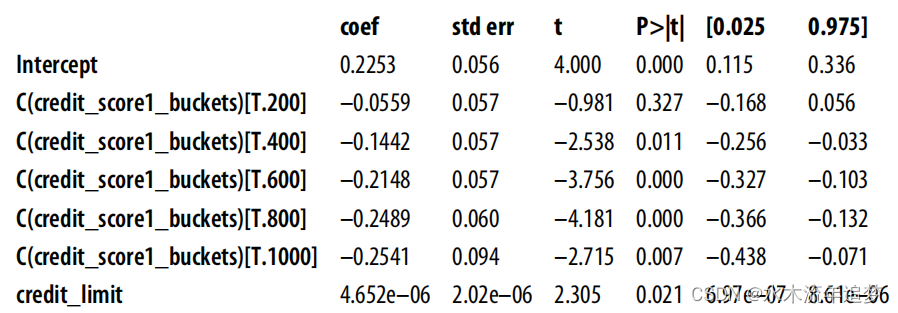

最后，這里只有一個斜率參數。添加虛擬變量來控制混雜因素后，每個組都有一個截距，但所有組的斜率都是一樣的。我們很快就會討論這個問題，但這個斜率將是各組回歸的方差加權平均值。如果繪制每個組的模型預測圖，您可以清楚地看到每個組只有一條線，但所有組的斜率相同：