近紅外光譜腦功能成像(fNIRS):1.光學原理、變量選取與預處理

一、朗伯-比爾定律與修正的朗伯-比爾定律

????????朗伯-比爾定律 是一個描述光通過溶液時被吸收的規律。想象你有一杯有色液體，比如一杯紅茶。當你用一束光照射這杯液體時，光的一部分會被液體吸收，導致透過液體的光變弱。朗伯-比爾定律告訴我們，透過液體的光的強度減少的程度與以下三個因素有關：

光的傳輸路徑長度：如果你增加液體的深度（即光穿過的路徑更長），光被吸收得更多，透過液體的光就更少。
吸光物質的濃度：如果液體中吸收光的物質（比如茶葉中的色素）更多，光被吸收得更多，透過液體的光就更少。
消光系數：這是一個物質的特性，表示這種物質吸收光的能力。不同的物質有不同的消光系數。

朗伯-比爾定律的數學表達式是：

OD=??C?L

其中：

OD是光密度（Optical Density），表示光被吸收的程度。
??是消光系數，表示物質吸收光的能力。
C?是吸光物質的濃度。
L?是光穿過的路徑長度。

????????修正的朗伯-比爾定律 是在朗伯-比爾定律的基礎上考慮了光在生物組織中的散射效應。在生物組織中，光不僅會被吸收，還會因為與組織中的微粒碰撞而改變方向，這種現象叫做散射。散射使得光在組織中的實際路徑比直線更長，因此光被吸收得更多。

????????修正的朗伯-比爾定律考慮了這一點，并引入了兩個新的參數：

路徑長度修正因子（DPF）：這個因子表示由于散射效應，光在組織中的實際路徑長度是直線長度的多少倍。
其他因素引起的光強衰減總和（G）：這個參數表示除了吸光物質之外，其他因素（如顱骨、腦脊液等）引起的光強衰減。

????????修正的朗伯-比爾定律的數學表達式是：

OD=??C?DPF?L+G

????????在實際應用中，由于 G 很難測量，通常我們只關注吸光物質濃度的相對變化，而不是絕對值。通過測量不同時間點的光衰減量，并利用修正的朗伯-比爾定律，可以求解出血紅蛋白濃度的相對變化，這對于研究腦功能等生物學過程非常有用。

二、因變量與自變量選取

???????在認知心理學領域，fNIRS腦成像實驗通過操縱自變量（如不同刺激或行為）來記錄血液動力學響應的變化，以此作為因變量，探索認知功能的神經基礎。因變量在fNIRS研究中通常表現為血液動力學響應的變化，具體可以取的值包括氧合血紅蛋白和脫氧血紅蛋白的濃度變化、腦區血流量的變化等。

????????自變量是實驗者可以操縱的因素，其不同取值稱為不同水平或條件。自變量可以通過操作化定義轉換為具體、可量化的指標，以便于實驗操作和結果分析。例如，受試者對任務的參與程度可以通過可能獲得的報酬數量來量化，通過設置不同等級的報酬來實現對受試者參與程度這個變量的操縱。自變量可以根據數據類型（類別變量或連續變量）、來源（作業/任務變量、環境變量、受試者變量）和可操作性進行分類。類別變量的例子如性別（男/女），連續變量的例子如學習成績（0—100的任意取值）。

????????單因素設計通過比較實驗條件與基線條件來計算神經響應指標。減法法則要求比較兩種任務的反應時差異，以分離特定認知過程的反應時。因變量在這種情況下可以取的值包括反應時、正確率等行為響應指標，以及神經活動引起的局部血液動力學響應。

????????共性法則通過多個減法實驗求得共性部分，提高腦區與認知成分關聯的可能性。因素設計同時操縱多個自變量，每個因素設置多個水平，以探索因素間的交互作用。因變量在因素設計中可以取的值包括不同實驗條件下神經活動的變化，如腦區血紅蛋白濃度的變化。

????????參數設計將感興趣的變量視為連續變量，通過在多個水平上觀察和記錄因變量的值，來確定自變量與神經響應之間的具體關系模式。因變量在參數設計中可以取的值包括隨著自變量變化，腦活動的變化模式，如線性或非線性關系。

三、數據預處理

去漂移（Detrending）：
- 原因：成像系統（如機器）在工作過程中逐漸升溫，環境溫度和光照的改變或受試者緩慢的頭動，通常表現為較長時間范圍內的緩慢波動。這種漂移會使fNIRS信號的基線發生改變，影響信號的穩定性和準確性。
- 方法：通過擬合信號中的線性或非線性趨勢項，然后從原始信號中減去這些趨勢項來實現去漂移。
- 數學原理：去漂移是通過擬合信號中的線性或非線性趨勢項，然后從原始信號中減去這些趨勢項來實現的。
- 公式：假設原始信號為?y(t)，擬合的趨勢項為?T(t)，去漂移后的信號為? $y_{d}(t)$ ，則有：
  $y_{d}(t) = y(t) - T(t)$
周期性噪聲濾波（Filtering）：
- 原因：周期性噪聲包括機器噪聲（如工頻噪聲50Hz和隨機熱噪聲高于2Hz）和生理噪聲（如心率約1Hz、呼吸約0.2—0.3Hz、Mayer wave約0.1Hz和極低頻的生理波動低于0.01Hz）。這些噪聲成分具有明顯的周期性波動特點，會影響信號的純凈度。
- 方法：通過高通濾波、低通濾波和帶通濾波等頻域濾波方法去除信號中具有明顯周期性波動特點的噪聲成分。
- 數學原理：濾波是通過在頻域中去除特定頻率成分來實現的。高通濾波、低通濾波和帶通濾波是常用的濾波方法。
- 公式：假設原始信號為?y(t)，濾波后的信號為? $y_{f}(t)$ ，濾波器的傳遞函數為?H(f)，則有：
  $Y_{f}(f) = Y(f) \cdot H(f)$
頭動噪聲和淺層噪聲去除：
- 頭動噪聲去除：
  - 原因：受試者頭動可能導致光極與頭皮接觸不良，這種頭動噪聲往往體現為信號中的大幅跳變。由于其出現時間和位置都較為隨機，傳統的頻域濾波預處理方法很難去除這種噪聲。
  - 方法：通過異常點檢測方法檢測到頭動噪聲，將任意時間點信號的幅值與一段時間內信號的平均幅值做對比，并且設置一定的閾限來標出異常點，然后去除這些異常點。
  - 數學原理：頭動噪聲通常表現為信號中的大幅跳變，可以通過異常點檢測方法來識別和去除。
  - 公式：假設信號的均值為?μ，標準差為?σ，閾值為?k，則異常點檢測公式為：異常點←∣y(t)?μ∣>k?σ
- 淺層噪聲去除：
  - 原因：頭皮、顱骨和腦膜等淺層組織中含豐富的毛細血管，呼吸、心跳等生理波動及任務相關的自主神經活動都會引起這些毛細血管中血紅蛋白濃度的變化，從而導致fNIRS光衰減量的變化（即淺層生理噪聲）。
  - 方法：通過短間隔通道法或空間濾波方法去除淺層噪聲。短間隔通道法利用額外的短間距fNIRS通道記錄淺層生理噪聲，再從信號中將其去除。
  - 數學原理：淺層噪聲可以通過短間隔通道法或空間濾波方法來去除。短間隔通道法利用額外的短間距fNIRS通道記錄淺層生理噪聲，然后從信號中減去這些噪聲。
  - 公式：假設淺層噪聲信號為?n(t)，原始信號為?y(t)，去除淺層噪聲后的信號為? $y_{n}(t)$ ，則有： $y_{n}(t) = y(t) - n(t)$

四、Python代碼實現

代碼如下：

import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import detrend, butter, filtfiltnp.random.seed(0)  # 模擬生成
t = np.linspace(0, 100, 1000)
y = np.sin(0.1 * t) + 0.1 * np.random.randn(1000)  # 添加正弦信號和噪聲
y += 0.01 * t  # 添加線性漂移# 去漂移
y_detrend = detrend(y)# 周期性噪聲濾波
def butter_bandpass_filter(data, lowcut, highcut, fs, order=4):nyq = 0.5 * fslow = lowcut / nyqhigh = highcut / nyqb, a = butter(order, [low, high], btype='band')filtered = filtfilt(b, a, data)return filteredfs = 10  # 采樣頻率
lowcut = 0.5
highcut = 2.0
y_filtered = butter_bandpass_filter(y_detrend, lowcut, highcut, fs)# 頭動噪聲去除
def remove_spikes(data, threshold=3):mean = np.mean(data)std = np.std(data)outliers = np.abs(data - mean) > threshold * stddata_clean = np.copy(data)data_clean[outliers] = meanreturn data_cleany_no_spikes = remove_spikes(y_filtered)# 淺層噪聲去除（實際應用中需要額外的短間距通道數據）
y_no_shallow = y_no_spikes - 0.1 * np.random.randn(1000)  fig, axs = plt.subplots(5, 1, figsize=(10, 15), sharex=True)plt.rcParams['font.family'] = 'serif'
plt.rcParams['font.size'] = 12
plt.rcParams['lines.linewidth'] = 1.5
plt.rcParams['lines.linestyle'] = '-'axs[0].plot(t, y, color='blue')
axs[0].set_title('Original Signal', fontsize=14)
axs[0].grid(True)axs[1].plot(t, y_detrend, color='green')
axs[1].set_title('Detrended Signal', fontsize=14)
axs[1].grid(True)axs[2].plot(t, y_filtered, color='red')
axs[2].set_title('Filtered Signal', fontsize=14)
axs[2].grid(True)axs[3].plot(t, y_no_spikes, color='purple')
axs[3].set_title('Signal without Spikes', fontsize=14)
axs[3].grid(True)axs[4].plot(t, y_no_shallow, color='orange')
axs[4].set_title('Signal without Shallow Noise', fontsize=14)
axs[4].grid(True)plt.xlabel('Time (s)', fontsize=14)
plt.tight_layout()
plt.show()

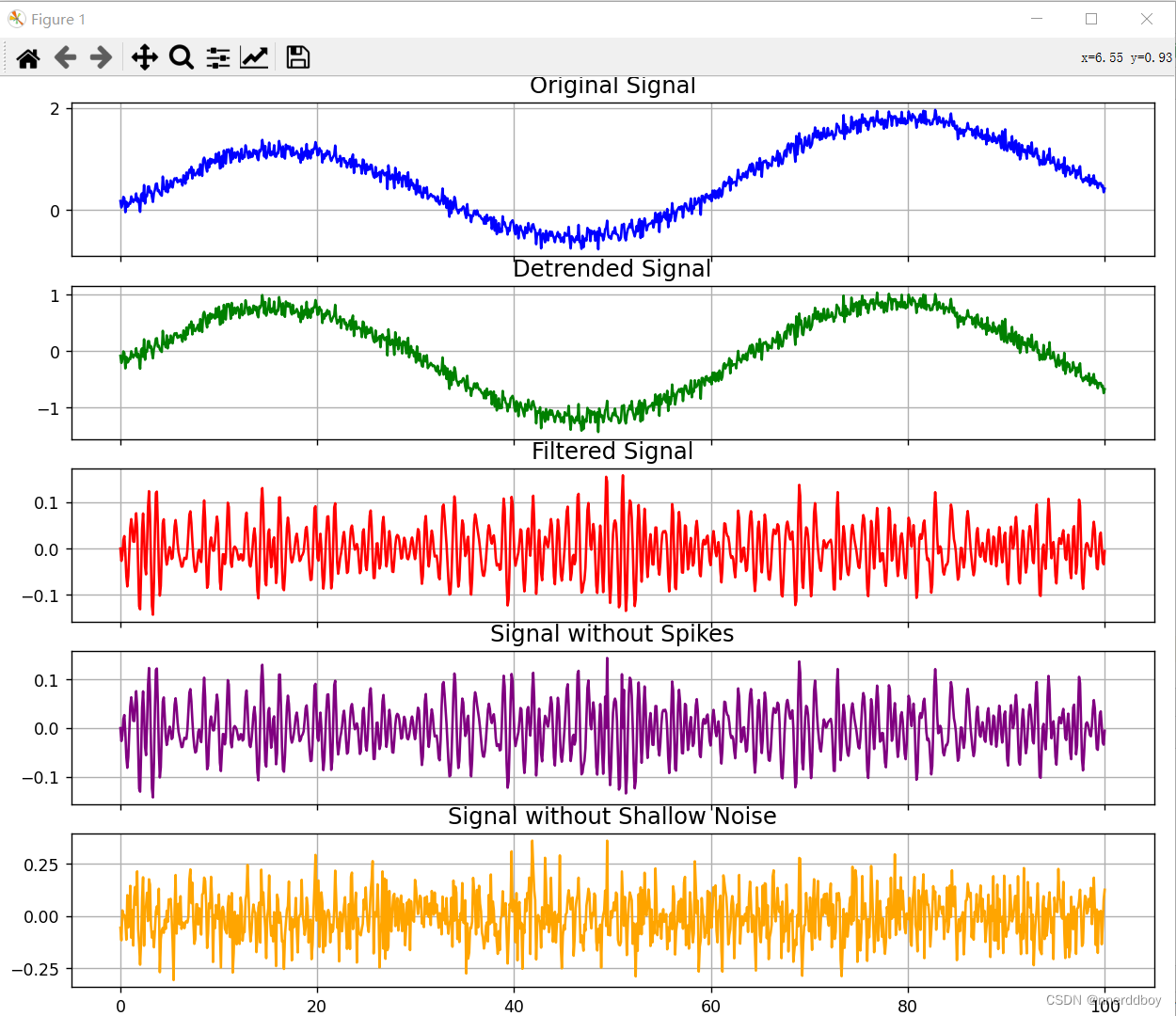
結果如下：