核方法總結（三）———核主成分（kernel PCA）學習筆記

一、核主成分

? ? 1.1 和PCA的區別

? ? ? ? ?PCA （主成分分析）對應一個線性高斯模型（參考書的第二章），其基本假設是數據由一個符合正態分布的隱變量通過一個線性映射得到，因此可很好描述符合高斯分布的數據。然而在很多實際應用中數據的正態性不能保證，這時用PCA建模通常會產生較大偏差。這時可以設計一個合理的非線性映射，將原始數據映射到特征空間，使數據在該空間的映射具有高斯性，在這個基礎可進行有效的PCA建模。即通過核函數間接映射到特征空間再間接進行建模，所以稱為核主成分分析；

? ? ? ?1.2 推導過程

? ? ? ? ?定義原始數據空間樣本為 $\left \{ x_{n} \right \}$ ,非線性映射為 $\phi \left ( x \right )$ ,且在原始空間和特征空間滿足如下歸一化條件。

? ? ? ? ? ? $\sum _{n}{x_{n}} = 0 \sum _{n}{\phi (x_{n})} = 0$ ? ?1------（1）

? ? ? 在映射空間的協方差矩陣可寫作：

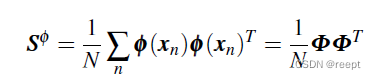? 1----（2）

上式中，假設 $\phi \left ( x_{n} \right )$ 有m維，則 $\phi \left ( x_{n} \right )$ $\phi \left ( x_{n} \right )^{T}$ 有m*m維。其中，在特征空間中求主成分v等價于求 $S^{\phi }$ 的特征向量：

$S^{\phi }v = \lambda v$ ? ?1----（3）

整理以上兩式可得：

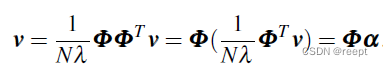1-----（4）

其中： $\alpha = \frac{1}{N\mu }\Phi ^{T}\nu$ ?，是一個N維向量，其中每一維對應一個數據點與特征向量v的內積，同時，上式說明在特征空間的特征向量v由所有數據樣本的向量加權平均得到，權重為 $\alpha$ ，轉化為對偶問題。將? $v = \Phi \alpha$ ?代回式 1 ----(4)? :

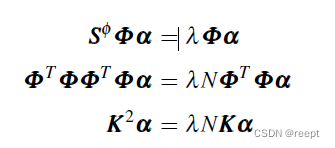? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??1----(5)、1-----(6)、1----（7）

其中 K為gram陣，?上式1—（7）右項左移，可以看出K選擇合適的核函數，會使K不等于空矩陣，因而可以推出：

$K\alpha = \lambda N\alpha$ ? ?1——（8）為1——（7）式的必要條件

考慮特征向量v應滿足 $v^{T}v$ ?=1 ,而 v= $\Phi \alpha$ ,有：

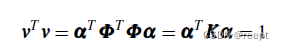1-----（9）

將1---（8）式左乘 $\alpha ^{T}$ 并代入上式，有：

$\lambda N\alpha ^{T}\alpha =1$ ? ?1----（10）

? ? $\alpha$ 可以通過下式求解：

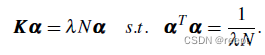? ?1------（11）

? ? 上式求解特征向量的方法是，求解左式的特征向量，再取 $\alpha$ ?=?? $\alpha \sqrt{\frac{1}{\lambda N}}$ ?就可以求得滿足約束的特征向量。解出 $\alpha$ 后，即可基于1—（4）式得到在特征空間的主成分向量。和標準PCA類似，我們可以求得多個主成分，組成主成分向量集{ $v_{i}$ }。

? ? 基于{ $v_{i}$ }可對任意測試樣本 $x$ 降維，且等價于在特征空間中計算 $\phi \left ( x_{} \right )$ 在各個主成分 $v_{i}$ 上的投影，計算如下：

? ?1———（12）

上式? $\alpha _{i,n}$ ?表示特征向量 $v_{i}$ 對應的權重的第n維（n=1.....N）。

? ? ? ? 雖然我們的目的是在特征空間進行主成分提取并給予得到的主成分對數據進行降維，但不需要在特征空間進行操作，所有計算都在原始空間中以核函數方式進行，計算得到的結果等價于在特征空間中進行。這使得可以在非常復雜的特征空間中對數據進行PCA建模，從而解決了原始數據的非高斯化問題，使PCA具有靈活性和可擴展性。

二、總結

? ? ??本文是學習《機器學習導論》（清華大學出版社，中文版，王東，2021年）的摘錄總結或筆記。

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/web/38423.shtml
繁體地址，請注明出處：http://hk.pswp.cn/web/38423.shtml
英文地址，請注明出處：http://en.pswp.cn/web/38423.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！