深入理解并應用KTT求解約束性極值問題

KT 很簡單，口訣記心端，等式求最優，不等式驗證——小飛打油

以后每期嘗試編一句口訣，幫助大家記憶，可以是打油詩，也可以是類似“奇變偶不變，符號看象限”的口訣，如果編的不好，也歡迎大家評論區幫我指正，感謝~。

一、前沿：什么是KKT

?KKT條件(Karush–Kuhn–Tucker conditions)是最優化（特別是非線性規劃）領域最重要的成果之一，是判斷某點是極值點的必要條件。

可理解好它需要用到梯度、松弛變量、對偶理論等知識，因此我也深知，想講好KKT條件是具有一定難度的。

我嘗試分兩部分講解，第一部分側重于理論部分，第二部分給出運用KKT條件進行數值和符號運算的Matlab代碼。基于此，大家可以非常方便地應用于自己的論文寫作。

在介紹KKT條件之前，先補充些基礎知識。

1. 何謂最優化問題：

要選擇一組參數（變量），在滿足一定的限制條件（約束）下，使設計指標（目標）達到最優值。

根據定義，請問前兩期的古諾模型和Stackelberg模型是最優化問題嗎？答案是肯定的，只不過它們均沒有約束，直接對決策變量求導便能得到最優值。

進一步，根據有無約束以及約束特征，可以將最優化問題分為以下三類，每類問題的求解方法也緊跟著列出。

2.?最優化問題分類：

無約束優化問題：直接求導、最速下降法、共軛梯度法、牛頓法等；
等式約束優化問題：拉格朗日(Lagrange)乘數法；
不等式約束優化問題：KKT條件。

大家做科研時也要分清楚自己的問題屬于哪一類，然后運用對應的求解方法。

以上知識點在本科的《運籌學》和《高等數學》課程中均學過。前兩類相對簡單，如果需要，歡迎評論或者后臺告知我，以后專門出幾期講解。

至于KKT條件，我深知大家會被課本上復雜的數學公式勸退，即使考前重溫，過段時間又會忘。

所以，本文不先從那些復雜公式入手，而是以我的理解，帶大家一起探索下Karush–Kuhn–Tucker這三個人，是如何發現并總結出KKT條件的。

我寫的每篇文章都盡力做到讓大家讀完后能有“這也不難嘛”的感受，也希望讀完本文后，能永久記住（即使忘了也能重新推導出來）KKT條件。

注：以下默認大家已了解拉格朗日乘數法（知道其數學形式就行，不用知道原理）

二、KKT條件理論部分

該部分先介紹KKT條件的核心思想，即λg(X*)=0公式的由來；再解釋為什么課本上的數學公式長那樣，最后再針對性地給出一些補充說明和數學證明。

1. KKT條件核心思想

時光倒流，假設你是還沒提出KKT條件的Karush本人，面對不等式約束優化問題，會如何思考呢？

先觀察下僅含有一個不等式約束的優化問題：

注：如果是最大化問題，即 maxf(X)，約束改寫為 g(X)≥0的形式（原因后文會解釋）。

既然默認還不知道KKT條件，所以目前咱么還不會解決該問題。但不急，想想咱們會啥？會求求導數，同時也會等式約束下的拉格朗日乘數法啊。

一步步來，先對f(X)函數求導吧（若X多維則是求梯度），即先不考慮g(X)≤0這個約束。

畢竟求導或求梯度，Karush和你都是會的。此時會得到“使f(X)取最小值時的最優X*”，進一步，如果將其值X*帶入約束g(X)，無非就以下三種情況。

（1）g(X*)<0

那正好滿足約束，X*就是我們要找的最優解。

猛然發現，此時該約束完全不起作用啊(稱為不起作用約束)，畢竟我們計算X*時壓根都沒考慮它。

（2）g(X*)=0

也就是最優解X*正好也讓約束取了等號。

這咱們也熟啊，這不轉化為含有等式約束的優化問題了嘛。如何求解？拉格朗日乘數法啊，安排~

（3）g(X*)>0

顯然此時的X*不滿足約束，應舍棄。

但這并沒有結束，我們需要給出一個解，那此時大家覺得X*會在哪？很簡單，無非又變回了情形（1）或（2）。

綜上，我們只需要分情況討論清楚若g(X*)<0和若g(X*)=0時，應該如何求解即可。

一通分析下來，大家或許此時感覺自己好像已經會了，不就是：

若g(X*)<0，約束不起作用，該問題轉化為 無約束優化問題求解；
若g(X*)=0，引入拉格朗日乘子λ，采用 拉格朗日乘數法求解嘛，其間，構造的 拉格朗日函數如下(這是拉格朗日乘數法的知識，不了解的同學可以自行簡單重溫下）。

理確實是這么個理，但人家數學家追求的是能否有個統一的形式來求解？這樣分類討論可不那么高大上啊。

既然都已經引進拉格朗日乘子λ了，那也得想辦法使得在g(X*)<0情形下，也要與λ有點關系。

考慮到若g(X*)<0，此時該約束不起作用，而已經構造好的拉格朗日函數中又有λ，怎么辦？

很簡單，讓拉格朗日函數中的λ=0即可！此時拉格朗日函數可不就簡化為L(x, λ)=f(X)了嘛。此時對L(x, λ)求導（等價于對f(X)求導）時既不用管約束，也沒有λ的干擾，簡直完美。

匯總一下就是：

（1）若g(X*)=0，引入拉格朗日乘子λ，并要求λ≥0；
（2）若g(X*)<0，要求λ=0。

那怎么統一呢？數學家靈魂附體！腦袋一拍，含淚發現，這不就可以采用λg(X*)=0的形式統一了嘛。

恭喜你，你代替Karush本人提出了λg(X*)=0！而這，就是KKT條件的精髓。

是不是有點難以置信，但確實，KKT條件的核心思想和公式其實已經講完了。

不復雜吧，基礎思想確實是很簡單的，畢竟早在1939年，Karush在其碩士學位論文里就已經給出了KKT條件。碩士生啊，哎，差距。

2. KKT條件的數學公式

掌握了思想，便可以更好地看懂課本上的公式了。

還是由簡到難，先給出僅含有一個不等式約束的KKT條件。

這里還需要借助上一部分給出的拉格朗日函數來理解。

簡單分析公式(1)-(4)可知：

式(1)：對拉格朗日函數求梯度(若X一維就是求導)，其中，下三角表示梯度；
式(2)：核心公式，要么λ=0，要么g(X*)=0（此處要求兩者不能同時為0）；
式(3)：拉格朗日乘子λ必須是正的（下一部分的圖示法有證明）；
式(4)：原問題自己的約束。

可見，式(1)和(2)都是等式，可以幫助我們求最優X*和λ，因為式(2)要分類討論，所以可能存在多個X*和λ；式(3)和(4)主要起驗證作用，幫助我們排除掉一些不滿足式(3)和(4)的X*和λ。

具體地，在應用KKT條件計算時，通常也是分類討論后先求解X*和λ，再驗證其是否滿足式(3)和(4)，從而排除一些解。

像上述僅含有一個約束的例子，只需要分兩類，通常是以拉格朗日乘子λ是否為0進行分類：

(1) 當 λ=0 時，計算X*的值，并驗證g(X*)≤0是否成立；
(2) 當 λ≠0 時，計算X*和λ的值，并驗證g(X*)≤0和λ≥0是否成立。

下面，將KKT條件推廣至含有多個等式約束和不等式約束的情況。也是課本上給初次學習KKT條件的同學提供的公式，勸退了好多人。

考慮的最優化問題為：

此時定義的拉格朗日函數為：

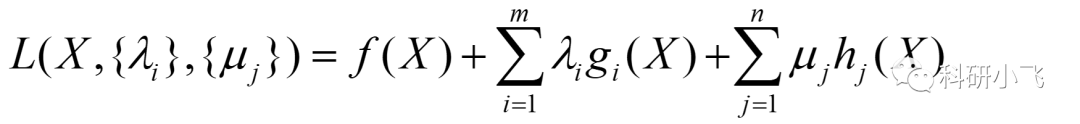
其中，{λi}指的是一系列的λ（有m個），同理{μj}也是。由于是多個約束，因此引入求和號∑。

其對應的KKT條件為：

不要被上述形式嚇到了，解題思路與之前敘述類似，就是用幾個等式計算最優值，用不等式驗證這些值，不滿足則排除。

即，利用式(1)(2)(3)求最優X*和 λi，然后通過式(4)和(5)驗證這些解是否可行，“可行”指的是這些解是否能讓(4)和(5)的不等號成立，不成立則排除。注意，μj是可以取任意值的，不受限制。因為它們是等式約束的拉格朗日乘子，不是不等式的乘子。

由于該問題有m個不等式約束，每個約束對應的拉格朗日/KKT乘子λi都可以“=0”或“≠0”。因此，需要分類討論的情況有2^m種。

分類詳情如下：(1) 當λ1=0，λ2≠0，......，λm≠0時；(2) 當λ1=0，λ2=0，......，λm≠0時；。。。。。。在此，不再展開，本文第四部分會給出算例來做具體說明。

至此，從特殊到一般的KKT條件講解完畢，總結一下，當我們應用KKT條件求解算例時，可以采用如下思路：

能解出最優解的一定是等式，故式(1)(2)(3)幫我們求最優解；
式(4)和式(5)是不等式，幫我們排除一些解，或者得到最優解的適用范圍。

這里有必要解釋下“得到最優解的適用范圍”這句話。其主要針對符號運算的情形，看完第四部分的算例，會有更深的理解，這里僅作為引子簡單提一下：

大家在寫論文時，建立的數學模型多是用 參數和變量表示的，不同情形下的最優解也是 符號表達式，因此 很難比較大小。
此時，只能通過式(4)和(5)，來得到 在什么條件（某符號表達式滿足某條件）下，最優解X*和對應的f(X*)值為多少，即需要 分類討論。

具體如何應用上述理論求解具體的算例，并撰寫Matlab代碼，放在第四部分講解，本部分著重講解理論。

三、KKT條件補充說明

該部分主要強調KKT條件的適用范圍和部分理論的數學證明。

1. 充分性、必要性說明

首先強調的是，KKT條件是判斷某點是極值點的必要條件，不是充分條件。換句話說，最優解一定滿足KKT條件，但KKT條件的解不一定是最優解。

對于凸規劃，KKT條件就是充要條件了，只要滿足KKT條件，則一定是極值點，且得到的一定還是全局最優解。

凸規劃指的是：目標函數為 凸函數，不等式約束函數也為 凸函數，等式約束函數是仿射的（理解成是 線性的也行）。這牽扯到另一個領域了，本文不再展開陳述。

補充：我知道很多同學會問，目標函數是凹函數就不能解了？并不是的，凸規劃/凸優化只研究凸函數的最小化問題，并且認為凹函數的最大化問題是與它等價的。畢竟凹函數只需加個負號就是凸函數了，所以在研究問題中，就不再提凹函數了。

2.?Min/Max與“≤0”和“≥0”的規定

這里指的是（該部分也是本文的重點部分，劃重點啦）：

（1）如果目標為最小化（Min）問題，那么不等式約束需要整理成“≤0”的形式；
（2）如果目標為最大化（Max）問題，那么不等式約束需要整理成“≥0”的形式；

以僅含有一個不等式約束的情形為例，最小化和最大化的優化問題要整理成如下形式：

該形式可以死記硬背，但時間一長，大家可能會忘記或記混了，下面，采用圖示法逐步展示為什么會有這個要求，該分析過程也展現了KTT條件的幾何思想。

上圖畫出了3條f(X)函數的等值線(圖中虛線)，以及右下角為可行域S（即約束條件規定的區域）和g(X)=0的曲線，最優解為X*。基于此，具體分析如下：

（1）f(X)函數值下降方向為左上方：
目標是 最小化問題，若下降方向為右下方，則最優解（圖中X*）一定不是在g(X)=0上，而是在可行域S內部；

由于KKT條件中第一條就需要計算f(X)和g(X)函數的梯度，所以，這里補充一個基礎知識：梯度方向垂直于函數等值線，指向函數值增長的方向。

基于此，我們嘗試畫出f(X)和g(X)函數的梯度方向：

（2）畫出f(X)的梯度方向（下圖紅色方向）：
梯度方向是函數值增長的方向，因此指向右下方；負梯度方向是函數值下降的方向，指向左上方；
（3）畫出g(X)的梯度方向（下圖藍色方向）：
由于曲線是g(X)=0，右下方是g(X)<0，是在下降，因此，g(X)函數值增長的方向就是左上方了。

由上述分析和上圖可知，在最優解X*處，f(X*)和g(X*)的梯度方向共線且方向相反。向量共線且方向相反在數學上的寫法就是：

負梯度向量是另一個梯度向量的λ倍。移項后發現，這不就是KKT條件的第一個等式嘛！

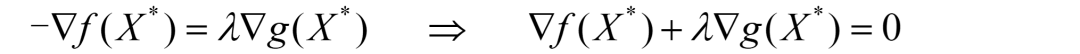
同時可知，λ的值只能取正值，因為g(X)的梯度方向與f(X)負梯度方向相同。這也是KKT條件要求?λ≥0?的原因。

基于以上分析可知：最小化問題的約束條件應該整理成“≤0”的形式，且λ≥0。

同理，最大化的分析不再展開，僅給出分析圖，有興趣的同學可以自己動手分析一下。

補充一點，請問大家，對于最大化問題，如果可行域也非要寫成g(X)≤0的形式，能行嗎？先別忙著否定，我們分析一下。

此時g(X*)的梯度方向就不再是右下方了（不是上圖了），而是f(X*)與g(X*)的梯度方向相同，有：

此時如上圖，要么KKT條件第一項改為“作差”，要么讓λ<0。無論哪一個，其實都是徒增煩惱。不如上來就規定約束寫成g(X)≥0來的方便。

因此，最大化問題的約束條件應該整理成“≥0”的形式，且λ≥0。

下面推廣到多約束條件的情形，僅是把梯度的共線變為梯度的線性組合，若不好理解，可跳過。

假設有起作用約束g1(X)和起作用約束g2(X)共同影響目標函數f(X)的梯度，又是怎么樣的圖形呢？

我們分別畫出g1(X)函數在X*處的梯度，如圖中藍色向量，其垂直于曲線g1(X*)=0；同理，畫出g2(X)函數在X*處的梯度，是另一個藍色向量。

至于f(X)函數的梯度，圖中畫出負梯度方向（函數值下降的方向），這樣畫的好處是可以直觀地看出三個梯度向量間的關系：

f函數的負梯度可以表示成g1函數和g2函數梯度的線性組合。則有如下公式：

簡單移項后，又發現了我們的老朋友：KKT條件的第一個等式。從圖中也可以看出，梯度向量之間的夾角為銳角，因此也有λ1≥0，λ2≥0的要求。

看完這部分內容，相信大家對于課本上關于KKT條件的的數學公式和圖形，能記憶也能自己推導了。當然，也歡迎大家收藏本文后，常常翻閱哈。

3. 正則性條件/約束規范說明

KKT條件對于目標函數和約束函數也是有要求的。該部分數學性較強，不好理解可跳過。

目標函數和約束函數（f、g1、... 、gm、h1、... 、hn函數）均為連續可微函數。

上述是我們熟知的要求，事實上，并不完全正確（嚴謹），還缺少一個regularity條件（也被成為正則性條件或者約束規范（constraint qualification））。

其含義指：以下方程組是線性獨立的。

其中，I?(X*)指的是起作用約束的集合。

這里不再深入展開，具體算例可參見B站視頻《KKT條件為什么用不了了》：

4. 幾類非光滑函數的轉化

上一節指出，運用KKT條件時，要求函數連續可微。可有些函數很常見，但卻存在不可微的點，此時就可以想辦法轉化下。

（1）目標函數：f(x) = max(x, x^2)

即目標函數f(x)存在不可微點：簡單畫圖可知，該函數在（0,0）點和（1,1）點處不可微。此時可以引入變量y，進行如下轉化。

強調一下，雖然這個看著簡單，但其實應用挺廣，比如對如下k個線性函數求最大。

（2）約束條件：g(x) = |x1| + |x2| ≤ 1

即約束條件g(x)存在不可微點：我們知道，絕對值函數的含義為|x| = max(x, -x)。而g(x)中有兩個絕對值，故可以如下轉化。

可見，g(x)函數轉化成了四個約束，四個約束都是線性，就可以用KKT條件了。當然，對于這種簡單的形式，畫圖求解也許會更方便。

總的來說，絕對值函數的線性化較為簡單，而更多的線性化方法/技巧，請參見之前寫的常見的線性化方法/技巧（上）和常見的線性化方法/技巧（下）或者令人拍案叫絕的線性化方法/技巧。

5. KKT條件與KT條件

這是一個小八卦，寫文章累，大家讀文章也累，供大家輕松一下。

1951年，Kuhn和Tucker發現了KKT條件并撰寫了論文將其正式發表出來，當然，此時他們不知道另一個K是誰，故命名為Kuhn-Tucker（庫恩塔克）條件，也就是KT條件。

很快，他們的成果引起了很多很多學者的重視。樹大招風，其中一些學者發現早在1939年，Karush在其碩士學位論文里邊已經給出了KKT條件，只是當時沒有引起廣泛關注而已。

不過，后來大家都承認Kuhn，Tucker，Karush三位都是獨立發現KKT條件的學者。故此后命名多加了個K。

四、數值與符號運算（重點）

簡單回顧下KKT條件：

還記得解題思路嗎？

能解出最優解的一定是等式，故式(1-3)幫我們求最優解；
式(4-5)是不等式，幫我們排除一些解，或者得到最優解的適用范圍。

這也是口訣“等式求最優，不等式驗證”的由來。

下面，我們來看下數值/符號運算中，KKT條件是如何求解最優化問題的。數值計算例子為求解最小化問題，符號運算例子為求解最大化問題。

先看下課本上的例題（其實是我編的），是如何應用KKT條件進行數值計算的。

1. 數值計算實操

我們想用KKT條件求解如下非線性最優化問題：

觀察約束，發現有“≥0”的形式，由本文第二三部分可知，需要統一轉化為“≤0”的形式，故上述問題的標準形式為：

基于該標準形式，構造的拉格朗日函數為：

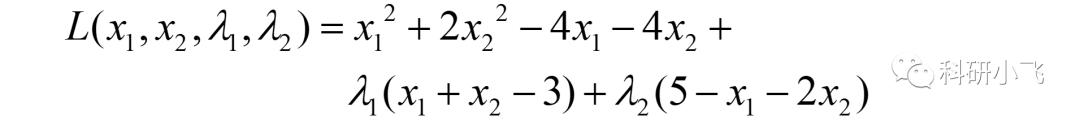
對其中的x1和x2分別求導，得到如下兩等式：

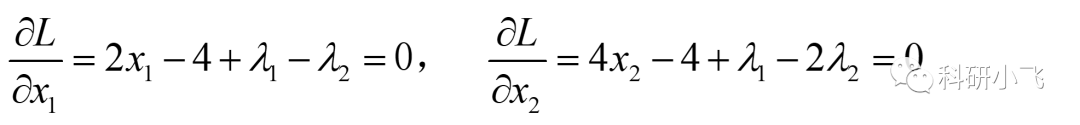
有些同學習慣用梯度表示，也可以，兩種方法一致，看大家熟悉哪種了：

數一下，有四個未知數，但求導后只有兩個等式方程，顯然還無法求解，此時KKT條件的核心公式λigi=0(i=1,2)就派上用場了。

λigi=0（兩者不同時為0）+ KKT條件中的不等式，具體含義為：

（1）若λ1=λ2=0，則g1＜0，g2<0；
（2）若λ1=0，λ2>0，則g1＜0，g2=0；
（3）若λ1>0，λ2=0，則g1=0，g2<0；
（4）若λ1>0，λ2>0，則g1=0，g2=0；

仔細觀察上述每一種情形，均包含了兩個等式方程，加上之前求導得到的兩個方程，總共四個方程，這回就可以求解四個未知數了。

那還等啥，直接求解吧。

（i）若λ1=λ2=0，則g1＜0, g2<0

無論哪種情形，主要是求解上面寫的求導后的/梯度方程，即：

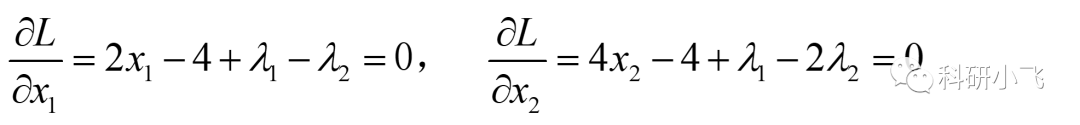
若λ1=λ2=0，則只需要求解x1，x2即可：

那x1=2, x2=1就是其中的一個解了嗎？

趕緊背下口訣“等式求最優，不等式驗證”！奧，原來還得驗證下該解是否滿足不等式g1<0 和g2<0。

將x1=2, x2=1帶入g1和g2，有：

很遺憾，兩個式子都無法使得?g1＜0 和 g2<0，故只能舍棄該解。

上一期內容理解好了的同學，會發現，此情形其實已經變為無約束問題（直接對f(X)求導后得到的解），然而它并不滿足約束，只能舍棄。

同時也說明，最優解一定會在某個約束的邊界上。那就繼續吧，看看是在g1=0，還是g2=0，還是g1=g2=0的邊界上。

（ii）若λ1=0, λ2>0，則g1＜0, g2=0

除了兩個求導后的方程，此情形多的兩個方程分別為λ1=0和g2=0，故累計又有四個方程，求解有：

此時顯然已經有λ2>0，故僅還需驗證“g1＜0”。

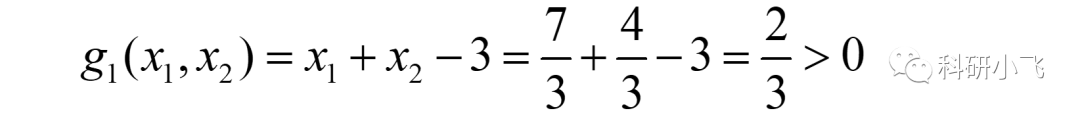
很可惜，不滿足g1＜0，故此解還是需要舍棄。

（iii）若λ1>0, λ2=0，則g1=0, g2<0

同2，也是四個方程，求解四個未知數，有：

發現此解與情形1的解一樣（僅是這個例子一樣，一般不會一樣），但帶入g2函數時，有：

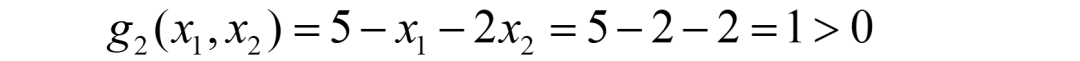
很可惜，依然不能使得g2<0，故該解還是需要舍棄。

（iv）若λ1>0, λ2>0，則g1=0, g2=0

此時，最優解在g1和g2函數的邊界上，聯立的四個方程為：

非常好，此時的λ1>0，λ2>0，滿足KKT條件，故x1=1, x2=2是本題的最優解。補充：一般四個方程，我是不會去手算的，編個簡單的Matlab代碼，就能快速求解：

syms x1 x2 t1 t2  % t1,t2分別指λ1,λ2
equ1 = 2*x1 - 4 + t1 - t2;  % 將上述四個方程對照著抄一下
equ2 = 4*x2 - 4 + t1 - 2*t2;  % 注意打上*，新手特別容易忘記
equ3 = x1 + x2 - 3;
equ4 = 5 - x1 - 2*x2;
[x1,x2,t1,t2] = solve([equ1 equ2 equ3 equ4], [x1 x2 t1 t2])

其中，因為Matlab中不方便打λ，所以我一般用t來代替，同時解四個方程用“[]”框起來，四個變量也用“[]”框起來。“[]”在Matlab中一般用來表示數組或矩陣。solve函數就是解方程用的。

綜上，x1=1, x2=2是本題的最優解。

2. 符號運算實操

下面，實操下科研中遇到有不等式約束的極值問題時，該如何利用KKT條件，并采用Matlab來編碼求解。

我編了個較為簡單清晰的算例，如下：

無約束定價問題：
若企業生產成本為c的產品，市場 需求函數為 D? = a - bp?(a, b 是參數， p為價格)，那企業的最優定價 p為多少？

上面這個算例是無約束的，簡單地，我再編兩個約束吧，變為有不等式約束的問題：

有不等式約束的定價問題：
約束1（針對需求）：假定需求量小于外生變量S；
約束2（針對價格）：企業規定價格不能低于m*c（m>1）；

則在這兩個約束下，企業如何定價才能使利潤最大？

先給出無約束問題下的解，決策最優定價p；再給出含有兩個不等式約束的最優定價決策。

（i）無約束定價問題

此種情形較為簡單，就是對利潤函數（為二次函數）求最優值：

具體的Matlab計算代碼如下：

clear
syms a b c p
Pi = (p - c)*(a - b*p);
equ = diff(Pi, p);  % 對利潤函數Pi中的p求導
Op_p = solve(equ, p);  % 求解方程equ=0中的p，命名為Op_p
Op_D = simplify(a - b*Op_p);  % 反代回需求函數，并化簡

其中牽扯到的diff()、solve()、simplify()以及后面會提及的subs()函數，在前幾期的古諾模型和Stackelberg模型有詳細描述，含義分別為求導、解方程、化簡、替換。在本文中不再贅述。

（ii）有不等式約束的定價問題

這里新增了兩個約束（雖然我承認有編的成分，但在實際中也是會發生的）：

約束1(針對需求)：假定需求量小于外生變量S：

約束2(針對價格)：企業規定價格不能低于m*c（m>1）：

綜上，我們有如下優化問題（寫成最大化問題的標準形式）：

注意，這里與數值算例的最小化問題不同，該問題是最大化問題，因此需將約束全部轉化為“≥0”的形式，并命名為g1、g2。

還記得第一步是什么嗎？對，基于標準形式，構造拉格朗日函數：

決策變量只有p，故僅對p求導即可：

顯然，這里僅有一個方程，要解出p、λ1、λ2三個未知數是不可能的，還需要兩個等式方程。而KKT條件就是用來給出剩下的兩個等式方程的。

這里附上上述過程的Matlab代碼（為方便敲代碼，依舊用t來代替λ）：

clear
syms a b c m p S t1 t2  % 定義需要用到的所有參數/變量
% 構造拉格朗日函數
L = (p-c)*(a-b*p) + t1*(S-a+b*p) + t2*(p-m*c);
% 對L中的決策變量p求導，命名為Equ
Equ = diff(L, p);
% 記錄一下Equ的表達式，后面要用
Equ = a + t2 - 2*b*p + b*t1 + b*c;

為方便后續計算，這里匯總下后面分類討論時，會反復用到的幾個表達式：

clear
syms a b c m p S t1 t2
% 1：利潤函數表達式
Pi = (p - c)*(a - b*p);
% 2：求導后的拉格朗日函數表達式
Equ = a + t2 - 2*b*p + b*t1 + b*c;
% 3：兩個約束條件的表達式
g1 = S - a + b*p;
g2 = p - m*c;

綜上，求導后的拉格朗日函數（Equ）含有p、λ1、λ2三個未知數，接下來分類討論的目的，就是利用KKT條件，解這三個未知數。已經有Equ=0方程了，剩下的兩個等式方程，分以下四種情況討論吧。

情形1：若λ1=λ2=0，則g1>0，g2>0

注意，這里與第一部分數值算例中的“g1<0, g2<0”不同，這里是最大化問題。也許有同學已經發現了，這其實就是無約束問題（兩個約束均沒有起作用），得到的最優解即為之前的p*=(a+bc)/2b。

還記得口訣嗎？等式求最優，不等式驗證。所以，剩下的就是檢驗該解是否滿足g1>0，g2>0。

因此，Matlab代碼編寫也分兩步。先給出此種情形下如何計算最優p和最大利潤，再計算得到該解需滿足的條件。

%% 情形1：當t1=t2=0時，g1>0, g2>0
equ = subs(Equ, [t1, t2], [0, 0]);  % 將t1=0, t2=0代入Equ函數
Op_p = solve(equ, p)  % 求最優p
Pi = simplify(subs(Pi, p, Op_p))  % 求最優利潤并化簡

時刻記住：在做符號運算時，求得的每一個解，都是有條件的。那么該解的條件是什么呢，就是g1>0，g2>0。既然S和m是我們新引進的參數，那么我們就來看看它倆需滿足什么條件。

% 將上述最優解代入g1，g2函數
g1 = subs(g1, p, Op_p)  % 將g1函數中的p，用Op_p的表達式代替
g2 = subs(g2, p, Op_p)
% 解出g1<0和g2<0時，S和m需要滿足的條件
solve(g1, S)
solve(g2, m)

代碼中solve函數解出來的解，就是S和m需要滿足的條件。

匯總下，就是只有當S和m滿足如下條件時，才會得到如下最優解：

情形2：若λ1=0，λ2>0，則g1>0，g2=0

此時由于g2=p-mc=0，故最優解就是p*=mc；將其帶入利潤函數，便得到最優利潤表達式。

當然，還需要看下想得到這個解，需要滿足的條件，即：λ2>0，且g1>0。將λ1=0，p*=mc帶入求導后的拉格朗日函數函數Equ，可以計算得到λ2的值，令其>0，加上g1<0的約束，便能最終該最優解適用范圍。代碼如下：

%% 情形2：當t1=0，t2>0時，g1>0, g2=0
% 先記錄下需要用到幾個函數表達式
clear
syms a b c m p S t1 t2
Pi = (p - c)*(a - b*p);
Equ = a + t2 - 2*b*p + b*t1 + b*c;
g1 = S - a + b*p;
?
equ1 = subs(Equ, [t1 p], [0, m*c]);  % 將t1=0，p=mc帶入Equ
equ2 = subs(g1, p, m*c);  % 將p=mc帶入g1約束
Pi = simplify(subs(Pi, p, m*c));  % 將p=mc帶入利潤函數并化簡
?
% 解出t2>0和g1>0時，S和m的范圍
t2 = solve(equ1, t2);  % 通過equ1=0解出t2表達式
solve(t2, m)  % 令t2=0，用m來表示
solve(equ2, S)  % 令equ2=0, 用S來表示

最后兩行代碼得到的解，就是為得到情形2下的最優解，需要滿足的條件，匯總有：

情形3：若λ1>0，λ2=0，則g1=0，g2>0

此時由于g1 = S-a+bp = 0，故最優解就是p* = (a-S)/b；將其帶入利潤函數，便得到最優利潤表達式。

再次回憶口訣：不等式驗證。該情形還需要滿足的條件，為：λ1>0，且g2>0。

將λ2=0，p* = (a-S)/b帶入Equ，可以計算得到λ1的值，令其>0，加上g2>0的約束，便能最終該最優解適用范圍。代碼如下：

%% 情形3：當t1>0，t2=0時，g1=0, g2>0
% 先記錄下需要用到幾個函數表達式
clear
syms a b c m p S t1 t2
Pi = (p - c)*(a - b*p);
Equ = a + t2 - 2*b*p + b*t1 + b*c;
g2 = p - m*c;
?
equ1 = subs(Equ, [t2 p], [0, (a-S)/b]);  % 將t2=0，p=(a-S)/b帶入Equ
equ2 = subs(g2, p, (a-S)/b);  % 將p=(a-S)/b帶入g2約束
Pi = simplify(subs(Pi, p, (a-S)/b));  % 將p=(a-S)/b帶入利潤函數
?
% 解出t1>0和g2>0時，S和m的范圍
t1 = solve(equ1, t1);  % 通過equ1=0解出t1表達式
solve(t1, S)  % 令t2=0，用S來表示
solve(equ2, m)  % 令equ2=0, 用S來表示

匯總代碼計算結果，有：

情形4：若λ1>0，λ2>0，則g1=0，g2=0

該情形下的最優解就是求解三方程Equ=0，g1=0，g2=0下的p、λ1、λ2值。

由于兩個約束都是關于p的一次函數，因此會得到矛盾的結論，故此種情形舍棄。

需要說明的是，科研中的很多問題會同時決策兩個變量，或者有非線性的約束等，此時兩個約束均取“=”是有解的。我這個算例編的簡單了，造成該種情形無解。

（iii）最優值間的相互比較

上述4種情形，3種情形均有最優解。很顯然，工作還沒做完，我們真正想得到的是哪些參數條件下，最優定價和最大利潤是多少？

如果是數值算例，很簡單直觀，拿著每種情形下的最大利潤比較下即可。

但符號運算就不得不分類討論，很多時候，我們甚至連某個表達式的正負號都無法確定。

但大家也不用太擔心相互比較會很麻煩。因為，只看利潤的話，真正需要比較的，其實只有情形2和情形3下的利潤大小。聰明的你知道這是為什么嗎？

答案揭曉：
情形1是無約束極值問題，相當于 全域搜索最優解，其利潤一定是 最大的；情形2和3下的最優解，均受到了一個約束g=0的 硬性限制，利潤一定會小一點；而情形4限制更強，要求 兩個約束均為0，這樣再去求利潤，一定是最小的。

因此，在情形1的參數范圍內，它就是老大，沒必要跟它比了。所以，重點還是落在情形2和情形3的參數范圍內，到底誰利潤更大。

為方便閱讀，避免前后翻看，情形1，2和3的結論匯總如下。

如上分析，在情形1的范圍內，利潤值一定最大，所以我們重點需要分析的是不滿足情形1的取值情況，即當S<(a-bc)/2和m>(a+bc)/2bc的情形。

你說巧不巧，S和m取值的對立面，恰恰對應著情形3和2。嚴肅地說，這不是巧，這是一定的。原因很簡單，同樣范圍競爭不過啊！

這里我想先強調下，大家時刻記住S和m是外生，相互獨立的。遇到S和m在同一個不等式關系里時，要想著它們是相互影響的，不能把它當成某個獨立的值。

什么意思呢，就是比如在分析情形2時，S取值要＞a-bcm，那我們需要和情形1中出現的(a-bc)/2比較大小嗎？

答案是否定的。因為a-bcm中m是可以變化的，而(a-bc)/2是定值。之所以強調這一點，只因為我曾經的分析犯過這個錯誤，結果把自己都搞暈了。

其實很簡單，高中知識就夠了。S＞a-bcm的形式，不就是畫出直線S=a-bcm后，然后取直線上方的部分嘛。畫在圖中就是：

簡單計算便知，直線S=a-bcm過交點（(a+bc)/2bc, (a-bc)/2），結合情形2中要求的m>(a+bc)/2bc，取值范圍就是上圖中的陰影部分。

同理，情形3的取值也就簡單了，將約束m<(a-S)/bc變化后，得到S<a-bcm，那不就是直線S=a-bcm的下方嘛。

結合情形3要求的S<(a-bc)/2，取值范圍如上圖中的陰影部分。

匯總下，就有下圖：

所幸，情形1-3的三個范圍的取值之間沒有存在交叉，但并不是每種算例都會這樣的，我這個算例較為簡單。

如之前分析，Pi1一定是最大的，通常我們需要花功夫比較下Pi2和Pi3。

至此，所有的問題就都分析完了。如果上述有錯誤，望大家批評指正。核心思想是會用KKT條件分類討論，并會比較不同情形間的最優利潤。

五、結語

總結下本文的核心：

（1）KKT條件是拉格朗日乘數法的推廣，理解引入λi的原因及作用；
（2）理解λg(X*)=0，就理解了KKT條件的精髓；
（3）掌握采用圖示法分析f(X)和g(X)的梯度關系。
（4）數值算例中，在運用KKT條件時，很容易發現矛盾（不滿足條件）的解，也很容易比較多個解的大小；
（5）符號運算時，若不考慮參數范圍，四種情形下的利潤大小關系一定有：情形1 > 情形2、3 > 情形4；
（6）比較利潤大小時，最好尋求其關于某個參數的一次或二次函數關系，切忌使用高次項參數。

為了方便大家記憶KKT條件的求解步驟，我編了個口訣，希望能對大家有所幫助：