一、基本概念

1. 定義

有兩個隨機均勻的樣本組 A、B，在同一個時間維度，對其中一個組B做出某種改動策略，實驗結束后分析兩組的數據。通過顯著性檢驗，判斷這個改動策略對于核心指標是否有顯著的影響。

2. 作用

驗證改動策略是否可行有效的方法。

3. 原理

1）大數定律（實驗次數足夠多時，隨機事件發生的頻率近似等于其概率）
2）中心極限定理（樣本量很大時，樣本均值近似服從給標準正態分布）
3）假設檢驗

二、實驗基本原則

同期性： 同一時期對于 A、B組進行實驗。
唯一性： 每一個實驗樣本都只存在于一個組里。
均衡性： 實驗樣本均衡分布在 A、B組（即 A、B組的實驗樣本量大致相同，A、B組的實驗樣本的比例占比大致相同）。
隨機性： 實驗樣本隨機分配到 A、B組。
樣本量足夠且獨立： 實驗樣本量足夠，同時實驗樣本間互不干擾。

三、實驗步驟

1.確定實驗目的
2.確定實驗變量
3.實驗指標設計： 除了核心指標（主指標），提出驅動指標、護欄指標。
4.樣本選擇： 選擇實驗群體，確定最少樣本量、樣本無關性。
5.流量設計： 分流（互斥）實驗，分層（正交）實驗，分流分層實驗、圈層實驗。
6.實驗與評估： 線上實驗，調整流量，分析數據，得到結論。
7.實驗放量： 結論通過，灰度實驗上線；不全量切換，先上線一部分。

四、實驗步驟詳解

1. 確定實驗目的

1）明確是否有必要進行 AB 測試的線上驗證，因為有一些問題通過數據分析方法也能解決。由于 AB 測試需要一定成本（如對用戶體驗的影響），所以要弄清目的，進行相關評估。
2）若確定要進行 AB 測試，要弄清本次實驗的目的是什么，是驗證個性化推薦功能對于客單價的提升與否還是其它方面。實驗目的明確了，才能決定后續的實驗變量、相關實驗指標、分流維度、實驗類型以及如何綜合評估實驗的效果。

2. 確定實驗變量

實驗目的明確后，也就確定了實驗變量。如不同的優惠券類型、是否添加個性化推薦功能、產品包裝樣式是否更改、小紅書發筆記是否添加封面等。

3. 實驗指標設計

3.1 實驗指標類型（按作用區分）

3.1.1 核心指標

其能最直接反應改動策略對用戶行為的影響。 例如，你的產品是把一個按鈕從紅色改為了藍色，AB 測試的目的就是看這種改動策略是否能讓更多的用戶點擊進入頁面，那么核心指標就可以選 CTR（Click Through Rate，即用戶點擊率）。核心指標的個數不宜太多，一般不超過三個。同時，核心指標的是否成功必須是能在短時間內被驗證，并能夠指示長期影響的指標。

3.1.2 驅動指標（跟蹤指標）

其不能直接衡量改動策略是否有效，但是能幫助檢測改動策略如何影響核心指標。 如果核心指標有異動，那么驅動指標能幫忙分析改動策略是如何導致核心指標發生變化的。比如在新界面上線后：
① 用戶購買量下降了（核心指標），同時用戶瀏覽量和在線時長都減少了。說明新的 UI 設計不合理，使用戶的體驗變差了，提前關閉 APP，導致了購買下降。
② 用戶購買量下降了（核心指標），但是用戶瀏覽量和在線時長都提高了。說明新的 UI 設計讓用戶愿意花更多時間瀏覽 APP。因為瀏覽時間變長了，用戶發現了很多喜歡的商品，但是由于選擇過多，反而讓用戶更難下定決心購買。

3.1.3 護欄指標

其用來檢測AB實驗是否對整體產品產生了負面影響。 例如，在測試抖音是否可以開啟給博主打賞這個功能的時候，我們并不希望抖音的日活數下降。護欄指標能幫助理解 AB 測試是否設置正確，以及 AB 測試是否對整體產品造成傷害。
① 護欄指標可以是產品的性能指標。 例如測試新的搜索引擎，一般也會對其性能進行衡量，例如：多少搜索成功完成，平均耗時多少？雖然這些度量并不完全決定是否發布新的搜索引擎，但是如果其表現很差，即使核心指標（搜索相關性）有一定提高，往往也不會發布新的產品。
② 護欄指標也可以是不直接影響的商業價值指標。 例如在做用戶增長實驗時，可以將用戶體驗作為護欄指標。雖然大部分的新產品和新功能都不應該影響用戶體驗， 但是將它們加入護欄指標可以對實驗結果更有信心。

3.2 實驗指標類型（按計算方式區分）

3.2.1 絕對值類指標

其是直接通過計算就能得到的單個指標，不需要多個指標計算得到。 一般都是統計該指標在一段時間內的總值或者均值，例如 DAU，平均停留時長等。這類指標一般較少作為 AB 測試的觀測指標。

3.2.2 比率類指標

其不能直接通過計算得到，而是通過多個指標計算得到。 例如某頁面的點擊率，我們需要先計算頁面的點擊數和展現數，兩者相除才能得到該指標。類似的，還有轉化率、復購率等。AB 測試的大部分指標都是比率類指標。

3.3 如何選擇評價指標

3.3.1 根據當前所處階段的目標

產品初期，公司通常以拉新作為主要業務目標。在這一階段，我們可以選擇點擊率、轉化率作為評價指標；在產品的發展期和成熟期，則會關注留存情況，我們可以選擇平均使用時間和頻率、留存率作為評價指標。

3.3.2 采用定性 + 定量相結合的方法

對于一些較為抽象的指標（例如用戶滿意度），我們可以使用一些定性的方法，例如問卷調查、用戶調研等進行定量的數據分析，來了解用戶的使用行為。把定性的用戶調研結果和定量的用戶使用行為分析結合起來，找出哪些用戶使用行為和和用戶滿意度有較強的關系。

4. 樣本選擇

4.1 最小樣本量計算公式（絕對值類指標，比率類指標通用）

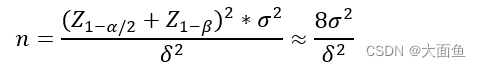
一般情況下：
置信水平：α = 0.05，Z1 - α/2 = 1.96
統計功效：1 - β = 0.8（β = 0.2），Z1 - β = 0.84
σ 代表的是樣本標準差，衡量的是整體樣本的波動性
δ 代表的是預期實驗組和對照組兩組數據的差值，比如說我們希望點擊率從20% 提升到 25%，那么δ = 5%

4.2 樣本標準差計算公式

4.2.1 絕對值類指標

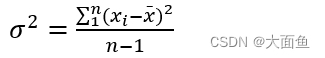
4.2.2 比率類指標

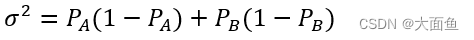
PA、PB 分別為對照組和實驗組的觀測數據。例如，我們希望點擊率從 20% 提升到 25%，那么 PA = 20%，PB = 25%

4.3 實驗周期計算公式（絕對值類指標，比率類指標通用）

每日實驗用戶量 = 用戶日活數（或者日均訂單數等指標）* 每日流量分配占比
每日流量分配占比（一般情況）：百萬級 → 3%，千萬級 → 1%，億級 → 0.1%

4.4 樣本量與實驗周期注意事項

4.4.1 樣本量不足問題

① 偶然誤差： 樣本量較小時，測試結果可能會受到偶然誤差的影響。例如，如果某一天的用戶行為發生異常，可能會對測試結果產生較大影響。
② 缺乏代表性： 如果實驗樣本不能很好地反映總體用戶群體的特點，那么測試結果可能無法推廣到所有用戶。

4.4.2 樣本量過大問題

可能造成實驗資源的浪費，同時可能影響迭代效率。

4.4.3 實驗周期長短問題

① 實驗周期果斷可能導致測試結果不穩定，在短時間內，用戶行為可能會發生變化。例如，節假日與促銷活動等都可能導致用戶行為出現波動，較長的實驗周期可以確保測試結果更加穩定。
② 一個實驗周期要盡量覆蓋用戶或者業務的一個周期性規律。

4.5 AA 測試

4.5.1 定義

AA 測試是指比較同一變量同一個版本的測試（例如新版本）。

4.5.2 目的

一般來說，AA測試用來檢驗AB測試結果的波動性、AB測試的用戶分流設計是否合理等。 如果 AB 測試設計合理，那么預期 AA 測試將得出實驗組與對照組沒有顯著差異的結論。但是如果 AA 測試結果差異顯著，說明本次實驗變量本身的效果波動就很大，原來 AB 測試的結果也不夠置信。

4.5.3 舉例

AA 測試比較兩個一模一樣按鈕的點擊率，測試流程與 AB 測試相同。如果最終結果顯示兩個按鈕的點擊率有統計意義上的顯著差異，那么有兩種可能：
① 出現了第一類錯誤： 這種可能性無法避免，因為假設檢驗本身預設了第一類錯誤的概率，通常為 5%，因此由于這種可能性而出現顯著性差異的概率是 5%。
② 測試在至少一個步驟上出現了問題： 這種可能性是最常見的，往往是測試對象分流的隨機性不夠，使得實驗組和對照組的測試對象有內在的差異，或者是指標的波動性過大。因此，需要對測試對象進行再隨機分組，重新進行統計檢驗，這個過程可能需要重復若干次，直到檢驗不出現顯著性差異，接下來則可以基于這一分組進行 AB 測試。

4.5.4 AA 測試時發現差異過大可能原因

樣本量不足，出現第一類錯誤，實驗觀測周期短，分流不科學，觀測指標本身不合理，組間均值差異過大，指標波動性大。

4.5.5 實驗指標波動性過大解決方法：CUPED

定義： 其是一種利用 AB 測試前的數據來縮減實驗指標方差，進而提高實驗靈敏度的方法，讓實驗指標更容易顯著，進而讓有效的改動策略上線，避免第二類錯誤（錯誤地接受策略上線前后沒有差異的原假設）的發生。
本質：對 X，Y 進行二維線性回歸，利用 AB 測試前的數據對實驗指標進行修正，在保證實驗指標均值估計無偏的情況下， 得到方差更低的新實驗指標，再對新實驗指標進行統計檢驗，這樣就可以得到更顯著的結果。
目的：在不增加樣本量的情況下，降低方差，使得實驗指標越可能顯著。
公式：

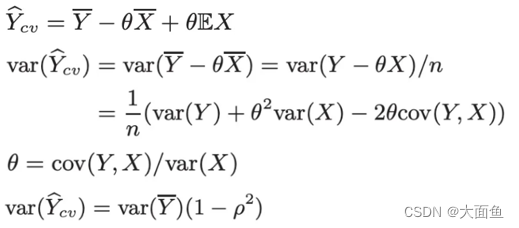
假設Y是我們實驗想觀察的實驗指標，現在用另一個變量 X 和常數 θ 構造一個新實驗指標，如圖（1）所示，為了讓其方差最小化，可以取常數 θ 為圖（4）所示。由此可以得出三個結論：
① 新實驗指標是 Y 的均值的無偏估計，其均值和Y的均值是一致的
② 新實驗指標的方差比 Y 的方差小，且影響大小的正是 X 和 Y 的協方差。
③ 如果能選取和Y高度相關的協變量X，那么新實驗指標的方差相比Y將會小很多。 大多數情況下最相關的還是原來這個指標。例如實驗要比較的是司機在線時長的差異，即 Y 為實驗中司機的在線時長數據，那么 X 就選司機在實驗前的在線時長數據。實驗前數據一般選取一周到兩周的周期。

4.6 樣本選擇要避免的問題（辛普森悖論）

4.6.1 定義

一般情況下，在進行分組研究并計算分項的比例（例如各種各樣的率）數據時，A 組的每一分項的數據都比 B 組數據要高，但是把各分項匯總起來計算總體數據時，A 組數據卻比 B 組數據低的現象。

4.6.2 產生原因

AB實驗中，兩組在不同細分領域中的數據分布不均衡造成的。

城市	對照組（一百萬用戶，點擊率）	實驗組（一百萬用戶，點擊率）	總體
北京	19710 / 900000 = 2.13%	1010 / 100000 = 1.01%	2.02%
上海	2560 / 100000 = 2.56%	11790 / 900000 = 1.31%	1.44%

例如上表中，北京對照組中的用戶數量占 90%，因此其總體的用戶轉化率受對照組影響最大。上海實驗組中的用戶數量占 90%，因此其總體的用戶轉化率受實驗組影響最大。但是上海實驗組的用戶轉化率要低于北京對照組的用戶轉化率，導致上海總體的用戶轉化率低于背景總體的用戶轉化率。

4.6.3 結構化梳理辛普森悖論觸發原因

統計對象	分項1指標	分項2指標	總體
統計對象1	q1 / p1	q3 / p3	(q1 + q3) / (p1 + p3)
統計對象2	q2 / p2	q4 / p4	(q2 + q4) / (p2 + p4)

基于上表，當出現以下 3 個數字特征的時候，即使統計對象1在兩個分項指標都高于（或低于）統計對象2，那么也有較大的概率，使得匯總數據出現反轉：
① 關注同一統計對象分母的大小比較：統計對象1中，分項1指標和分項2指標的分母 p1 和 p3 不是一個數量級（例如 p1 是百萬級，而 p3 是萬級）。
② 關注同一統計對象在不同分項指標中，比例值的比較：統計對象1中，分項1指標的比例值（q1 / p1）顯著高于（或低于）分項2指標的比例值（q3 / p3）（例如 65% vs 35%）。
③ 關注兩個統計對象在不同分項指標中，分母比例分布的比較：統計對象2的分母 p2 和 p4，與統計對象1的分母 p1 和 p3 的分布明顯不同（例如統計對象1的分母 p1 和 p3 的比例是 9:1，但統計對象2的分母 p2 和 p4 的比例是 6:4）。

4.6.4 減少辛普森悖論的產生

① 分析測試結果前，做好合理性檢驗。如果沒有進行合理性檢驗，最好的解決辦法就是重新跑實驗，看兩組在不同細分領域的分布不均衡會不會消失。如果分布不均衡的情況沒有消失，就說明這很可能不是偶然事件，這時就要檢查是否是工程或者實施層面出現了問題，由此造成了分布的不均衡。
② 進行合理正確的流量分割，保證實驗組和對照組的用戶特征是一致的，并且都具有代表性，可以代表總體用戶特征。
③ 在實驗設計上，如果我們覺得兩個變量對實驗結果都有影響，那就應該把這兩個變量放在同一層進行互斥實驗，不要讓一個變量的實驗動態影響另一個變量的實驗。
④ 在實驗實施上，我們要對實驗結果進行多維度的細分分析。除了總體對比，也要看看細分受眾群體的實驗結果，不要以偏概全。一個實驗版本提升了總體活躍度，但可能降低了年輕用戶群體的活躍度，那么這個實驗版本可能算不上好版本。一個實驗版本提升了總體營收 0.1%，似乎不起眼，但是上海地區的年輕男性用戶群體的購買率提升了 20%，這個實驗版本就很有價值。

4.7 學習效應

4.7.1 定義

當我們想通過AB測試檢驗非常明顯的變化時，比如改變產品的交互界面和功能，老用戶往往適應了之前的交互界面和功能，對他們來說需要一段時間來適應和學習新產品，所以老用戶在適應階段的行為跟平時有些不同。

4.7.2 分類1（新奇效應）

在AB測試中，由于用戶對于新變化有很強的好奇心，愿意去嘗試，進而導致測試初期的結果偏離常態。這種現象通常會在新版本或新功能推出的一段時間內發生，隨著時間的推移，用戶的新奇感逐漸消退，行為才會恢復到正常狀態。

4.7.3 分類2（改變厭惡）

在AB測試中，由于用戶對于新變化比較困惑，產生抵觸心理，例如，電商網站的購物車功能原本在屏幕的右下方，交互界面改變后，購物車功能的位置變味了屏幕的左上方，用戶可能需要一點時間才能找到，導致其可能受負面情緒影響提前關閉了界面，這時短時期內的指標就會下降。

4.7.4 避免學習效應的方法

① 觀察實驗組的指標隨時間（以天為單位）的變化情況： 沒有學習效應的情況下，實驗組的指標隨時間的變化是相對穩定的。但是有學習效應時，因為學習效應是短期的，長期來看會慢慢消退，那么實驗組的指標就會有一個隨時間慢慢變化的過程，直到穩定。
② 只關注實驗組與對照組的新用戶： 學習效應是老用戶為了適應新的變化產生的。那么可以現在兩組中找出老用戶，只在兩組的新用戶中分別計算實驗指標，最后再比較這兩個實驗指標。如果在新用戶的比較中沒有得出顯著結果（樣本量充足的情況下），但是在總體的比較中得出了顯著結果，那么就說明這個新變化對于新用戶沒有影響，但是對于老用戶有影響。
③ 延長測試時間： 等到實驗組的學習效應消退，再比較兩組的結果。

5. 流量設計

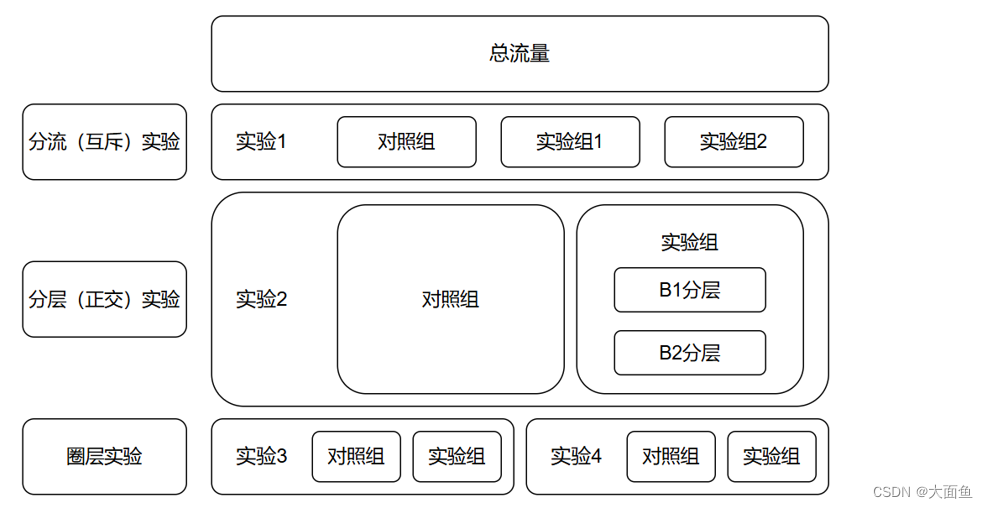
5.1 分流（互斥）實驗

用戶分流（互斥）是指按照地域、性別、年齡等把用戶均勻地分為幾個組，1 個用戶只能出現在 1 個組中。但是實際情況中，往往會同時上線多個實驗，拿廣告來說，有針對樣式形態的實驗，有針對廣告位置策略的實驗，有針對預估模型的實驗。如果只是按照這種分流模式來，在每組實驗放量 10% 的情況下，整體的流量只能同時開展 10 個實驗。這個實驗的效率是非常低的。為了解決這個問題，提出了用戶分層、流量復用的方法。例如上圖中，對照組、實驗組1、實驗組2 通過分流的方式分為 3 組流量，此時對照組、實驗組1、實驗組2 是互斥的，即對照組流量 + 實驗組1流量 + 實驗組2流量 = 100% 試驗流量。

5.2 分層（正交）實驗

同一份流量可以分布在多個實驗層，也就是說同一批用戶可以出現在不同的實驗層，前提是各個實驗層之間無業務關聯，保證這一批用戶都均勻地分布到所有的實驗層里，達到用戶正交的效果就可以。所謂的正交分層，就是每一層用完的流量進入下一層時，一定均勻的重新分配。第一層中每個實驗的流量會重新分組進入到第二層中的每個試驗中。所以整個流量有一個分散，合并，再分散的過程，保證第二層中的每個實驗分配的流量雨露均沾，這就是所謂的流量正交，從而實驗流量復用的效果。例如上圖中，流量流過實驗組中的B1分層、B2分層時，B1分層、B2 分層的流量都與實驗組的流量相等，相當于對實驗組的流量進行了復用，即 B1 分層流量 = B2 分層流量 = 實驗組流量（其實這一部分的圖是同時互斥與正交的，此處為了方便而單獨解釋了正交）。

5.3 圈層實驗

通常手中比較大的增長點做完了，更多的會去做用戶的精細化運營，滿足某些用戶群體沒有被很好滿足到的需求，以帶來業務上的增長。例如多日無播放行為的用戶做一個圈層，做做引導。例如下載頁無內容的用戶做一個圈層，做做優質內容的推薦。例如某一興趣標簽的用戶做一個圈層，提供更匹配的服務等。

6. 實驗與評估

6.1 Z檢驗公式

6.1.1 絕對值類指標

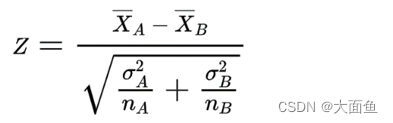
6.1.2 比率類指標

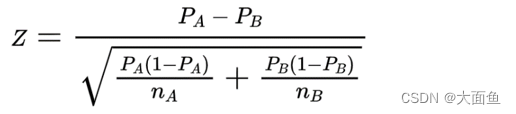
6.2 第一類錯誤與第二類錯誤

① 第一類錯誤： 其表示一個功能的改動，本來不能帶來任何收益，但是我們誤以為它能給我們帶來收益。
② 第二類錯誤： 其表示一個好的產品，本來可以帶來收益，但是由于統計誤差，導致我們誤以為它不能給我們帶來收益。
③ 關注重點： 往往在實際的工作中，第一類錯誤是我們更加不能接受的。 也就是說，我們寧愿砍掉幾個好的產品，也絕對不能讓一個壞的產品上線。因為一個壞的產品上線會給用戶體驗帶來極大的負面影響，而這個負面影響會非常大程度的影響到用戶日活數以及留存率。在現實生活中，我們把留存或者把日活提升一個百分點都已經是一個非常了不起的優化了。但是通常要實現 1% 的留存率，都需要花費很長時間，但是如果想要留存率下降 1% 的話，可能就是一瞬間的事情。
④ 避免兩類錯誤的方法
增加樣本量： 較大的樣本量可以提供更準確的總體估計和更高的統計功效。
控制顯著性水平（α），考慮統計功效（1 - β）
多次獨立重復實驗： 可以減小隨機誤差的影響，提供更穩定一致的結果。
仔細選擇樣本： 樣本的選擇應該盡可能代表總體，避免選擇偏倚。采用隨機抽樣的方法，并確保樣本特征與分布與總體一致，可以減小偏差的風險。

6.3 實驗評估流程

6.3.1 整體指標分析

通過實驗指標的點估、區間估計、P 值、實驗指標趨勢等，評估改動策略效果是否顯著。

6.3.2下鉆指標維度

當實驗重點關注部分群體時，分析中往往對用戶進行下鉆，聚焦用戶評判效果；或者當實驗效果不及預期時，會下鉆維度分析原因。

6.3.3 case 抽取分析

當實驗正負向較明顯時，可以將極端 case 單拎出來，分析可能的原因。

6.4 實驗效果不顯著的原因與解決方法

實驗效果不顯著的原因
① 第一類：線上改動策略不佳，無明顯差異。
② 第二類：實驗靈敏度不夠高。
針對第二類問題的解決方法
① 增加樣本量： 只要實驗組和對照組的差值及樣本方差不變的情況下，樣本量足夠大，總是可以得到顯著性的結果。
② 減少樣本的方差： 減少離群值的影響，可以采用CUPED的方法。
③ 更換為方差更小的實驗指標： 例如購物平臺的實驗指標一開始是用戶購買的平均金額，我們可以更換為用戶是否購買。對于同一批樣本，用戶是否購買服從0-1分布，樣本的方差要比用戶購買的平均金額小很多。

6.5 實驗統計上顯著，實際不顯著可能原因

可能的原因是我們在AB測試當中所選取的樣本量過大，導致和總體數據量差異很小，這樣的話即使我們發現一個細微的差別，它在統計上來說是顯著的，在實際的案例當中可能會變得不顯著了。 舉個例子，對應到我們的互聯網產品實踐當中，我們做了一個改動，APP的啟動時間的優化了0.001秒，這個數字可能在統計學上對應的P值很小，也就是說統計學上是顯著的，但是在實際中用戶0.01秒的差異是感知不出來的。那么這樣一個顯著的統計差別，其實對我們來說是沒有太大的實際意義的。所以統計學上的顯著并不意味著實際效果的顯著。

7. 實驗放量

7.1 放量流程

實驗放量階段，需要綜合考慮三個因素：效率、質量、風險。 對于一個實驗，我們希望在評估正向的前提下，盡快上線。但往往由于策略bug、新功能不符合預期、用戶體感不好等問題，使得在放量階段需要更加謹慎，以下為一個標準的放量流程。

7.1.1 第一階段（小流量階段）

此階段銜接在小流量評估后，整體放量比例控制在5%以下，評估實驗是否對產品北極星指標有負向影響。同時驗證策略的觸發，以及排查是否存在潛在風險。在無風險的前提下，建議持續3-5日左右，進入下一個階段。

7.1.2第二階段（放量階段）

在這個階段，隨著樣本量的逐漸放開，實驗的結果也會更加精準。同時，可能會出現流量壓力等問題，因此在此階段需要跟進放量，觀察是否有出現問題。逐級放量建議持續至少一周，以觀測周中和周末的影響。

7.1.3第三階段（長期存放階段）

針對部分實驗，如果希望長期觀測實驗效果，可以保留5%以下的原始策略，作為反轉桶。

五、相關代碼實踐

kaggle 數據集鏈接：https://www.kaggle.com/datasets/zhangluyuan/ab-testing

import numpy as np
import pandas as pd
from scipy.stats import normdf = pd.read_csv('ab_data.csv')
df =  df.drop('landing_page', axis=1)
df# 對 group 進行分組，再對每組中 converted 列中的值分別進行計數
df.groupby('group')['converted'].value_counts()# 以上代碼的運行結果
group      converted
control    0            1294791             17723
treatment  0            1297621             17514
Name: count, dtype: int64# 先按照 group 列進行分組，然后對 converted 列進行求和，最后取出 control 組的求和結果
x_control = df.groupby('group')['converted'].sum().loc['control']
# 統計 group 列中為 control 的數據的數量
n_control = df[df['group'] == 'control'].shape[0]
# 先按照 group 列進行分組，然后對 converted 列進行求和，最后取出 treatment 組的求和結果
x_treatment = df.groupby('group')['converted'].sum().loc['treatment']
# 統計 group 列中為 treatment 的數據的數量
n_treatment = df[df['group'] == 'treatment'].shape[0]
print(f'Number of convertion in the control group: {x_control}')
print(f'Number of total data in the control group: {n_control}')
print(f'Number of convertion in the treatment group: {x_treatment}')
print(f'Number of total data in the treatment group: {n_treatment}')
# 計算對照組與實驗組中的轉化率
# 方法1
control_conversion_rate = x_control / n_control
treatment_conversion_rate = x_treatment / n_treatment
print(f'\nConversion rate of the control group: {control_conversion_rate:.6f}')
print(f'Conversion rate of the treatment group: {treatment_conversion_rate:.6f}')
# 方法2 (推薦，因為方便)：按照 group 列進行分組，然后選擇 converted 列，并對該列應用均值聚合函數。最后，從聚合結果中分別提取出 control 組和 treatment 組的均值，即兩組的轉化率。
p_control_conversion_rate = df.groupby('group')['converted'].agg(np.mean).loc['control']
p_treatment_conversion_rate = df.groupby('group')['converted'].agg(np.mean).loc['treatment']
print(f'\nConversion rate of the control group: {p_control_conversion_rate:.6f}')
print(f'Conversion rate of the treatment group: {p_treatment_conversion_rate:.6f}')# 以上代碼的運行結果
Number of convertion in the control group: 17723
Number of total data in the control group: 147202
Number of convertion in the treatment group: 17514
Number of total data in the treatment group: 147276Conversion rate of the control group: 0.120399
Conversion rate of the treatment group: 0.118920Conversion rate of the control group: 0.120399
Conversion rate of the treatment group: 0.118920# 不計算合并方差
variance_control = p_control_conversion_rate * (1 - p_control_conversion_rate) * 1 / n_control
variance_treatment = p_treatment_conversion_rate * (1 - p_treatment_conversion_rate) * 1 / n_treatment
variance = variance_control + variance_control
print(f'Variance: {variance}')
# 計算合并方差
p_pooled = (x_control + x_treatment) / (n_control + n_treatment)
pooled_variance = p_pooled * (1 - p_pooled) * (1/n_control + 1/n_treatment)
print(f'\nP pooled: {p_pooled:.6f}')
print(f'Pooled variance: {pooled_variance}')# 以上代碼的運行結果
Variance: 1.4388828544267224e-06P pooled: 0.119659
Pooled variance: 1.4308828178078735e-06# 計算標準誤差
SE = np.sqrt(variance)
print(f'SE value: {SE}')
# 計算 Z 檢驗的值
Z_test = (abs(p_treatment_conversion_rate - p_control_conversion_rate)) / SE
print(f'\nTest statistics of Z test: {Z_test}')
# 計算在標準正態分布圖上，對應的 x 軸的分位點的值
alpha = 0.05
Z_critical_value = norm.ppf(1-alpha/2)
print(f'\nValue on the standard normal distribution: {Z_critical_value}')
# 計算 p 值時，單側檢驗不用乘 2，雙側檢驗要乘 2
p_value = norm.sf(Z_test)
print(f'\nP value: {p_value}')
if p_value <= alpha:print('There is a statistical significance.')
else:print('There is no statistical significance.')# 以上代碼的運行結果
SE value: 0.0011995344323639577Test statistics of Z test: 1.233478384744372Value on the standard normal distribution: 1.959963984540054P value: 0.10869866814352241
There is no statistical significance.