1. 前言

前文我們實現了二叉樹前中后三種遍歷方式的遞歸版本，非常簡單. 接下來我們來實現一下其迭代版本.

2. 二叉樹的前序遍歷

(1). 題

給你二叉樹的根節點?root?，返回它節點值的?前序?遍歷。

示例 1：

?

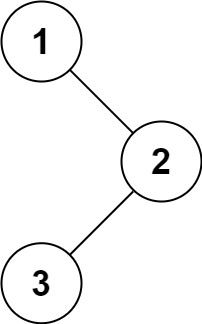
輸入：root = [1,null,2,3]
輸出：[1,2,3]

示例 2：

輸入：root = []
輸出：[]

示例 3：

輸入：root = [1]
輸出：[1]

示例 4：

?

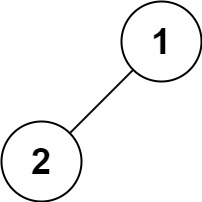
輸入：root = [1,2]
輸出：[1,2]

示例 5：

?

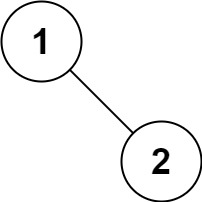
輸入：root = [1,null,2]
輸出：[1,2]

提示：

• 樹中節點數目在范圍?[0, 100]?內
• -100 <= Node.val <= 100

(2). 思路

遞歸調用系統棧，迭代算法自己構造一個棧來模擬. cur指針指向根節點，while循環，條件只要cur不為空并且棧不為空，不斷將元素添加到數組中(根)，直到訪問到最左的葉子節點(左). 此時將其從棧彈出，訪問右節點(右). 如果該右節點為空，則繼續彈棧，訪問彈棧出的節點右節點.不斷繼續此過程.

(3). 解

class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();if (root == null) {return list;}Deque<TreeNode> stack = new LinkedList<>();TreeNode cur = root;TreeNode p;while (cur != null || !stack.isEmpty()){if (cur != null) {stack.push(cur);list.add(cur.val);cur = cur.left;} else {p = stack.pop();cur = p.right;}}return list;}
}

3. 二叉樹的中序遍歷

(1). 題

給定一個二叉樹的根節點?root?，返回?它的?中序?遍歷?。

示例 1：

?

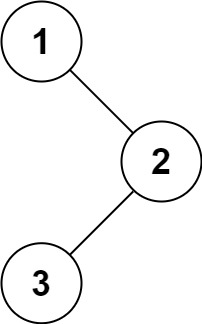
輸入：root = [1,null,2,3]
輸出：[1,3,2]

示例 2：

輸入：root = []
輸出：[]

示例 3：

輸入：root = [1]
輸出：[1]

提示：

• 樹中節點數目在范圍?[0, 100]?內
• -100 <= Node.val <= 100

(2). 思路

while循環開始，如果cur不為null則一直壓棧(左)，直到cur為null，彈棧，并訪問該節點(根)，繼續討論該節點的右孩子(右). 繼續彈棧，該節點的左孩子部分已經完成，訪問該節點的值，繼續討論其右孩子.直到循環結束.

(3). 解

class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();if (root == null) {return list;}Deque<TreeNode> stack = new LinkedList<>();TreeNode cur = root;TreeNode p;while (cur != null || !stack.isEmpty()){if (cur != null) {stack.push(cur);cur = cur.left;} else {p = stack.pop();list.add(p.val);cur = p.right;}}return list;}
}

4. 二叉樹的后序遍歷

(1). 題

給你一棵二叉樹的根節點?root?，返回其節點值的?后序遍歷?。

示例 1：

?

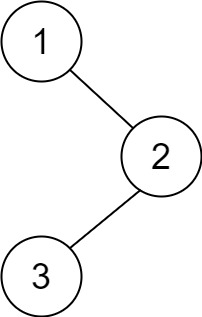
輸入：root = [1,null,2,3]
輸出：[3,2,1]

示例 2：

輸入：root = []
輸出：[]

示例 3：

輸入：root = [1]
輸出：[1]

提示：

• 樹中節點的數目在范圍?[0, 100]?內
• -100 <= Node.val <= 100

(2). 思路

思路如下.

(3). 解

class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> al = new ArrayList<>();if (root == null) {return al;}TreeNode cur = root;TreeNode pop = null;Deque<TreeNode> stack = new LinkedList<>();while (cur != null || !stack.isEmpty()){//只要cur不為null, 一直訪問左節點, 并不斷入棧if (cur != null) {stack.push(cur);cur = cur.left;} else {//此時棧頂元素的左孩子為null 即其左孩子無需處理TreeNode peek = stack.peek();//peek.right == null表明棧頂元素的右孩子無需處理//peek.right == pop表明棧頂元素的右孩子已經處理完畢if (peek.right == null || peek.right == pop){//訪問該棧頂元素, 并彈出al.add(peek.val);//記錄處理的節點pop = stack.pop();} else {//else表明該棧頂元素的右孩子待處理, 則cur = peek.rightcur = peek.right;}}}return al;}
}