一、KNN算法的定義

? ? ? ? KNN（K-Nearest Neighbors）算法，是一種簡單而有效的監督學習方法。它既可以用在分類任務，也可用在回歸任務中。KNN算法的核心思想：在特征空間中，如果有一個數據點周圍的大多數鄰居屬于某個類別，則該數據點也應該被歸為那么類別（分類任務中）。或者其預測值應該接近這些鄰居的平均值（回歸任務中）。

二、K值的選擇

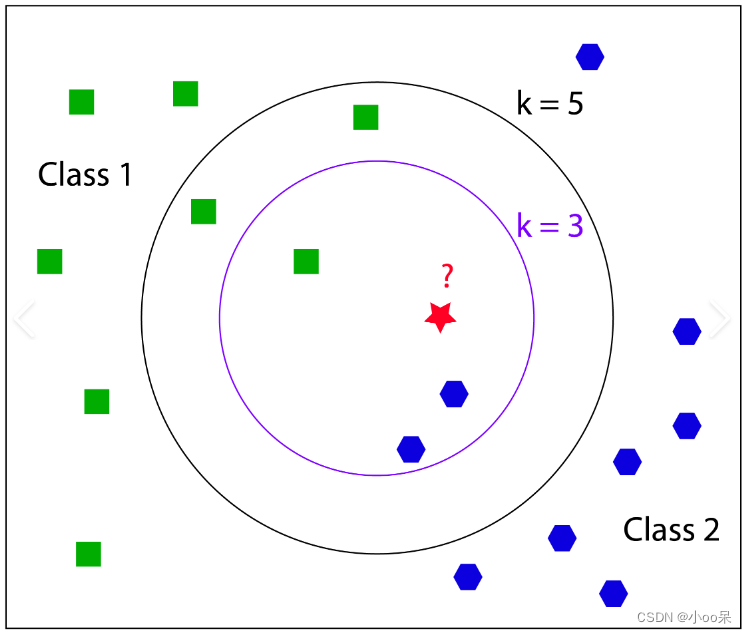
????????K是一個重要的超參數，其大小直接影響預測的準確性。

• K值較小可能導致過擬合，因為模型變得對噪聲敏感；
• K值較大可能導致欠擬合，因為模型可能開始考慮遠處的、不那么相關的鄰居。

? ? ? ? 可以依據經驗來選擇，雖然經驗可以在某些情況下提供指導，但確定K值通常依賴于更系統的方法。以下是幾種常用的策略：?

（1）依據經驗

? ? ? ? 經驗一：對于K的初試選擇，K值常常在較小的范圍內試探，比如從1開始，逐漸增加到如5、10、15等。這個范圍的選擇是為了平衡過擬合和欠擬合的風險。K值太小（如K=1）時，模型可能對噪聲很敏感，容易過擬合；而K值太大時（比如大于訓練樣本數的平方根），模型可能會忽略局部特征，趨向于簡單多數類，導致欠擬合。

? ? ? ? 經驗二：如果數據集較小，K值通常不宜設置得太大，以免引入過多的噪聲或稀釋關鍵信息。相反，大數據集可能允許較大的K值。

? ? ? ? 經驗三：有時推薦使用奇數K值以避免出現平票的情況，尤其是當類別分布較為均衡時。如果采用偶數K且遇到類別票數相同的情況，可能需要額外的規則來決定歸屬類別，如隨機選擇或考慮距離加權。

（2）交叉驗證

????????這是一種常用的模型選擇方法，也可以用來確定K值。具體操作是將數據集分割成訓練集和驗證集，然后對于每個候選的K值，使用訓練集訓練模型并在驗證集上評估性能。重復這一過程，選擇在驗證集上表現最好的K值。

三、KNN算法步驟

（1）訓練階段

????????KNN算法非常不同，它的訓練階段不需要學習任何模型參數，它只是簡單地存儲所有的訓練數據集，不做任何進一步的處理。

（2）預測階段

① 數據準備與設置參數

????????收集數據：首先，需要有一組已經分類好的訓練數據集，每條數據包括多個特征和對應的標簽（分類任務）或數值（回歸任務）。特征選擇與標準化：選擇對分類或回歸有用的特征，并對數據進行預處理，如縮放特征值到同一尺度，以消除特征間因量綱不同造成的影響。選擇K值：這是最重要的超參數之一，決定了在分類或回歸時要考慮的最近鄰居的數量。

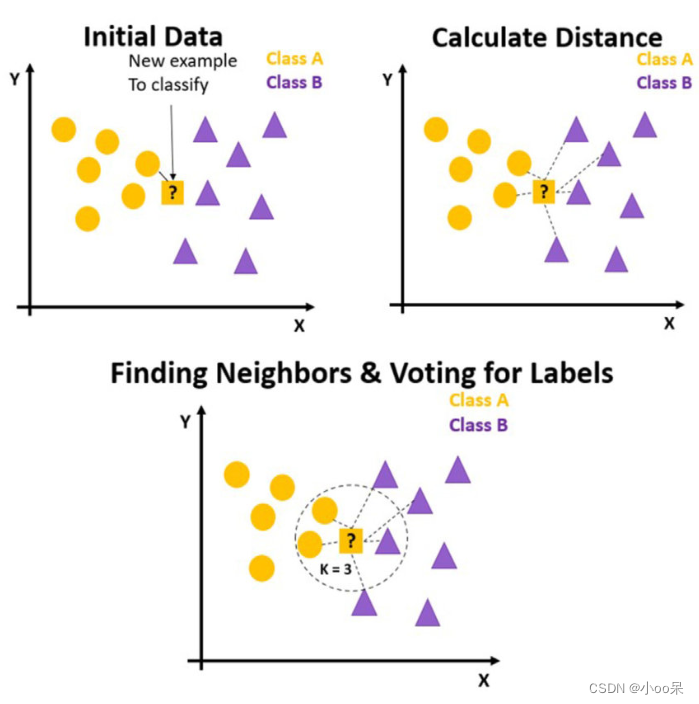
③ 計算距離

????????對于每一個新的未知類別的樣本，計算其與訓練集中每個樣本之間的距離。常用的距離度量方法有歐氏距離、曼哈頓距離、切比雪夫距離等。

④ 選擇鄰居并做出決策

????????根據計算出的距離，找出距離最近的K個訓練樣本作為鄰居。?

• 分類任務：查看這K個鄰居中哪個類別的樣本最多，將新樣本歸為該類別。可以簡單計數或距離加權（考慮距離遠近）后決定。
• 回歸任務：取這K個鄰居的目標值的平均值（或加權平均）作為新樣本的預測值。

⑤ 評估模型并優化調整

????????使用交叉驗證或獨立的測試集來評估模型的性能，包括準確率、召回率、F1分數等。根據評估結果，可能需要調整K值或考慮其他改進措施，如使用不同的距離度量方法、維度減少（如PCA）、或采用KD樹等數據結構加速最近鄰搜索。

四、KNN與K-means的關系

（1）KNN與K-means的區別

• 應用場景不同：KNN用于有監督學習的分類和回歸問題，而K-means用于無監督學習的聚類任務。
• 對初始條件敏感性不同：K-means算法對初始聚類中心的選擇非常敏感，不同的初始化可能導致完全不同的聚類結果。KNN算法則不受初始條件影響，因為它是基于查詢點周圍最近鄰的直接比較，沒有迭代優化聚類結構的過程。
• K的意義不同：在KNN中，K代表考慮的最近鄰居的數量，直接影響模型的復雜度和預測的穩定性。較大的K值可以減少噪聲的影響，但可能使邊界變得模糊；較小的K值則可能對噪聲敏感，但邊界更清晰。在K-means中，K代表期望形成的簇的數量，需要事先指定，且選擇合適的K值對聚類效果至關重要。錯誤的K值可能導致過分割或欠分割問題。

（2）KNN的優缺點

優點：簡單易懂，原理直觀，實現起來相對直接。無需訓練，沒有復雜的訓練過程，計算負擔主要在預測時。既能分類又能回歸。

缺點：計算成本高，特別是對于大規模數據集，需要計算測試樣本與所有訓練樣本之間的距離，非常耗時。存儲需求大，需要存儲整個訓練數據集。對異常值敏感，訓練數據中的異常點可能嚴重影響預測結果。特征尺度影響大，不同特征的尺度差異可能導致距離度量失真，通常需要進行特征縮放。