---

1.最長遞增子序列

1.題目鏈接

• 最長遞增子序列

---

2.算法原理詳解

• 題目解析：從每個位置，依次計算其最長遞增子序列
  

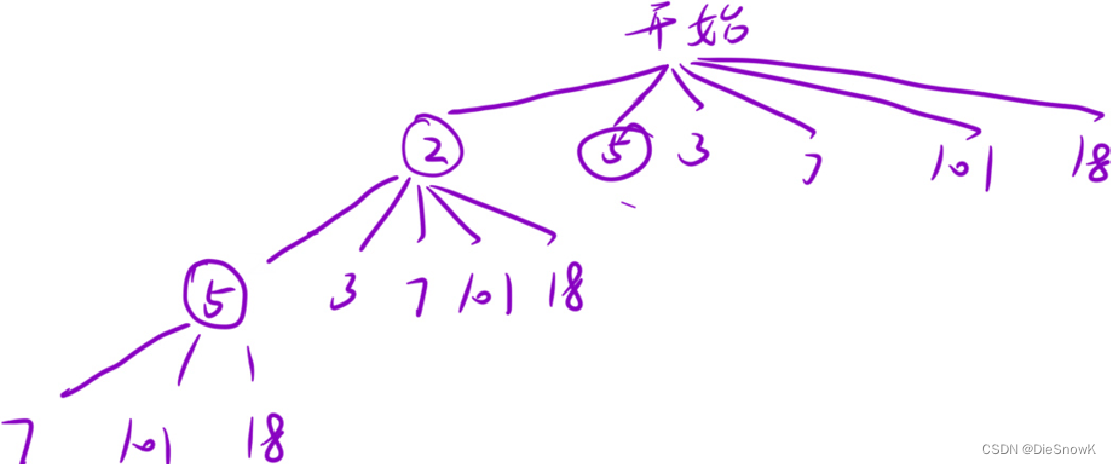
• 思路選擇：

  • 暴搜(遞歸) -> 本題會超時:P
  • 記憶化搜索
  • 動態規劃

• 嘗試：暴搜 -> 記憶化搜索 -> 動態規劃

• 暴搜：

  • DFS()設計：int DFS(nums, pos) -> 每次從pos位置找最長遞增子序列
  • 函數體：依次從pos位置往后枚舉，更新本次最長遞增子序列

• 本題有大量重復要計算的值，故可以用記憶化搜索

• 記憶化搜索：

  • 備忘錄：vector<int> mem
  • 返回之前，把結果存在備忘錄中
  • 遞歸之前，查找一下備忘錄是否有要找的值

• 動態規劃

  • 注意：本題是前面的值依賴后面的值，所以**填表順序要從后往前填**

---

3.代碼實現

// v1.0 暴搜
class Solution 
{
public:int lengthOfLIS(vector<int>& nums) {int ret = 0;for(int i = 0; i < nums.size(); i++){ret = max(ret, DFS(nums, i));}return ret;}int DFS(vector<int>& nums, int pos){int ret = 1; // 細節：初值為1for(int i = pos + 1; i < nums.size(); i++){if(nums[i] > nums[pos]){ret = max(ret, DFS(nums, i) + 1);    }}return ret;}
};
-------------------------------------------------------------------------------
// v2.0 記憶化搜索
class Solution 
{vector<int> mem;
public:int lengthOfLIS(vector<int>& nums) {mem.resize(nums.size());int ret = 0;for(int i = 0; i < nums.size(); i++){ret = max(ret, DFS(nums, i));}return ret;}int DFS(vector<int>& nums, int pos){if(mem[pos] != 0){return mem[pos];}int ret = 1; // 細節：初值為1for(int i = pos + 1; i < nums.size(); i++){if(nums[i] > nums[pos]){ret = max(ret, DFS(nums, i) + 1);    }}mem[pos] = ret;return ret;}
};
-------------------------------------------------------------------------------
// v3.0 動態規劃
int lengthOfLIS(vector<int>& nums) 
{int n = nums.size();vector<int> dp(n, 1);int ret = 0;for(int i = n - 1; i >= 0; i--) // 枚舉每個位置{for(int j = i + 1; j < n; j++) // 依次枚舉后面的值的最長子序列{if(nums[j] > nums[i]){dp[i] = max(dp[i], dp[j] + 1);}}ret = max(ret, dp[i]);}return ret;
}

---

2.猜數字大小 II

1.題目鏈接

• 猜數字大小 II

---

2.算法原理詳解

• 題目思路解析：

  • 每次給出一個數據范圍，從中找出花費最少的一次
  • 但是當一個結點的左右子樹返回時，要取最大的，因為要確保"能獲勝的最小金額"，就要讓左右子樹的兩種情況都能實現
  • 最優解：取最小是在該范圍內，每個數對應的最終結果取最小
    

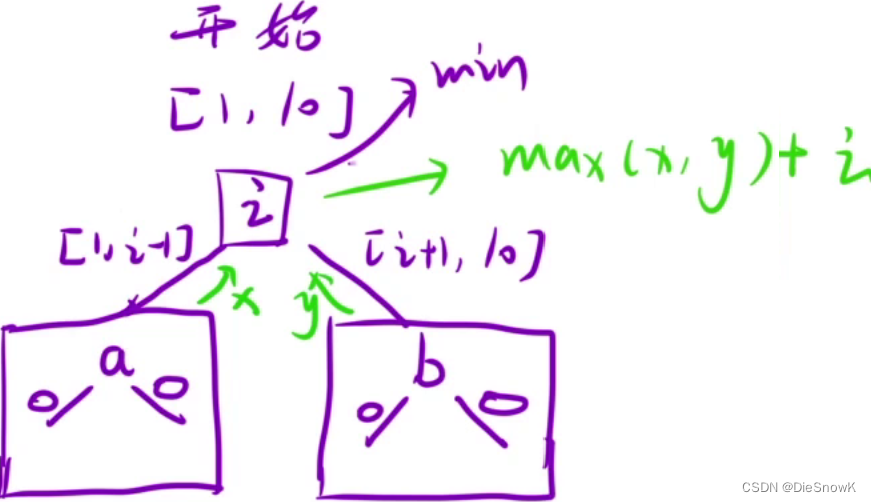
• 思路選擇：

  • 暴搜(遞歸) -> 本題會超時:P
  • 記憶化搜索

• 暴搜：

  • DFS()設計：int DFS(int left, int right) -> 每次從[left, right]區間內找出最小的
  • 函數體：依次遍歷[left, right]中的各個數，遞歸分析左右?樹，求出所有情況下的最?值
  • 遞歸出口：
    • left > right：區間不存在，返回0
    • left == right：就是最后的一個結果，此時無需花錢，返回0

• 本題有大量重復要計算的值，故可以用記憶化搜索
  

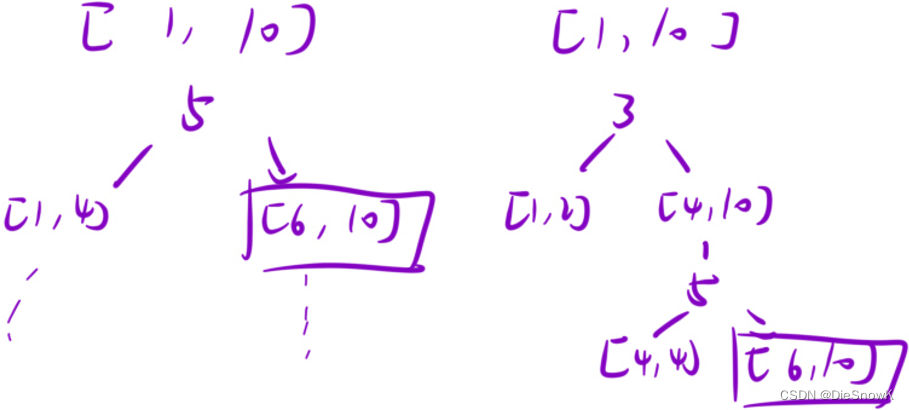
• 記憶化搜索：

  • 備忘錄：vector<int> mem
  • 返回之前，把結果存在備忘錄中
  • 遞歸之前，查找一下備忘錄是否有要找的值

---

3.代碼實現

// v1.0 暴搜
class Solution 
{
public:int getMoneyAmount(int n) {return DFS(1, n);}int DFS(int left, int right){if(left >= right){return 0;}int ret = INT_MAX;for(int i = left; i <= right; i++) // 選擇頭結點{int x = DFS(left, i - 1);int y = DFS(i + 1, right);ret = min(ret, max(x, y) + i);}return ret;}
};
------------------------------------------------------------------------
// v2.0 記憶化搜索
class Solution 
{vector<vector<int>> mem;
public:int getMoneyAmount(int n) {mem.resize(n + 1, vector(n + 1, 0));return DFS(1, n);}int DFS(int left, int right){if(left >= right){return 0;}if(mem[left][right] != 0){return mem[left][right];}int ret = INT_MAX;for(int i = left; i <= right; i++) // 選擇頭結點{int x = DFS(left, i - 1);int y = DFS(i + 1, right);ret = min(ret, max(x, y) + i);}mem[left][right] = ret;return ret;}
};

---

3.矩陣中的最長遞增路徑

1.題目鏈接

• 矩陣中的最長遞增路徑

---

2.算法原理詳解

• 題目解析：遍歷數組，對每個位置來一次DFS即可
• 思路選擇：
  • 暴搜(遞歸) -> 本題會超時:P
  • 記憶化搜索
• 本題有大量重復要計算的值，故可以用記憶化搜索
  

---

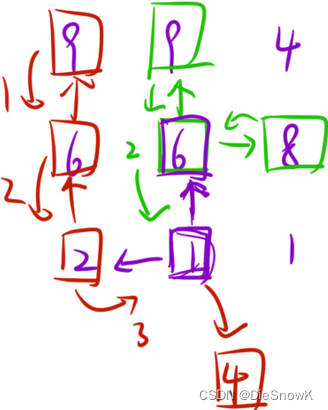
3.代碼實現

// v1.0 暴搜
class Solution 
{int n, m;// "方向"向量數組int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};
public:int longestIncreasingPath(vector<vector<int>>& matrix) {n = matrix.size(), m = matrix[0].size();int ret = 0;for(int i = 0; i < n; i++){for(int j = 0; j < m; j++){ret = max(ret, DFS(matrix, i, j));}}return ret;}int DFS(vector<vector<int>>& matrix, int i, int j){int ret = 1;for(int k = 0; k < 4; k++){int x = i + dx[k], y = j + dy[k];if(x >= 0 && x < n && y >= 0 && y < m && matrix[x][y] > matrix[i][j]){ret = max(ret, DFS(matrix, x, y) + 1);}}return ret;}
};
---------------------------------------------------------------------------
// v2.0 記憶化搜索
class Solution 
{int n, m;vector<vector<int>> mem;// "方向"向量數組int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};
public:int longestIncreasingPath(vector<vector<int>>& matrix) {n = matrix.size(), m = matrix[0].size();mem.resize(n, vector<int>(m, 0));int ret = 0;for(int i = 0; i < n; i++){for(int j = 0; j < m; j++){ret = max(ret, DFS(matrix, i, j));}}return ret;}int DFS(vector<vector<int>>& matrix, int i, int j){if(mem[i][j] != 0){return mem[i][j];}int ret = 1;for(int k = 0; k < 4; k++){int x = i + dx[k], y = j + dy[k];if(x >= 0 && x < n && y >= 0 && y < m && matrix[x][y] > matrix[i][j]){ret = max(ret, DFS(matrix, x, y) + 1);}}return mem[i][j] = ret;}
};