一、GBDT (Gradient Boosting Decision Tree) 梯度提升決策樹

GBDT是一種迭代的決策樹算法，是一種基于boosting增強策略的加法模型,由多棵決策樹組成。每次迭代都學習一棵CART樹來擬合之前 $t?1$ 棵樹的預測結果與訓練樣本真實值的殘差，最終所有樹的結論累加起來做最終答案。GBDT在被提出之初就和SVM一起被認為是泛化能力較強的算法。

XGBoost對GBDT進行了一系列優化，比如損失函數進行了二階泰勒展開、目標函數加入正則項、支持并行和默認缺失值處理等，在可擴展性和訓練速度上有了巨大的提升，但其核心思想沒有大的變化。

GBDT主要由三個概念組成：

• Regression Decision Tree（即DT)
• Gradient Boosting（即GB)
• Shrinkage（縮減）

1.1 回歸樹

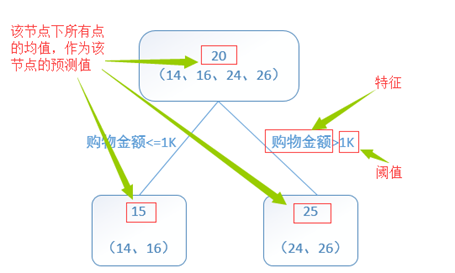
回歸樹總體流程類似于分類樹，區別在于，回歸樹的每一個節點都會得到一個預測值。以年齡為例，該預測值等于屬于這個節點的所有人年齡的平均值。分枝時窮舉每一個feature的每個閾值找最好的分割點，但衡量最好的標準不再是最大熵，而是最小化平方誤差，來找到最可靠的分枝依據。

關于回歸樹，具體可參考CART中對回歸樹的介紹：決策樹之CART（分類回歸樹）詳解

1.2 梯度提升樹

提升樹是迭代多棵回歸樹來共同決策。當采用平方誤差損失函數時，每一棵回歸樹學習的是之前所有樹的結論和殘差，擬合得到一個當前的殘差回歸樹。殘差的意義如公式：殘差 = 真實值 - 預測值。
GBDT的核心就在于，每一棵樹學的是之前所有樹結論和的殘差，這個殘差就是一個加預測值后能得真實值的累加量。比如A的真實年齡是18歲，但第一棵樹的預測年齡是12歲，差了6歲，即殘差為6歲。那么在第二棵樹里我們把A的年齡設為6歲去學習，如果第二棵樹真的能把A分到6歲的葉子節點，那累加兩棵樹的結論就是A的真實年齡；如果第二棵樹的結論是5歲，則A仍然存在1歲的殘差，第三棵樹里A的年齡就變成1歲，繼續學。
??舉個例子：訓練一個提升樹模型來預測年齡。簡單起見訓練集只有4個人，A,B,C,D，他們的年齡分別是14,16,24,26。其中A、B分別是高一和高三學生；C,D分別是應屆畢業生和工作兩年的員工。如果是用一棵傳統的回歸決策樹來訓練，會得到如下圖1所示結果：

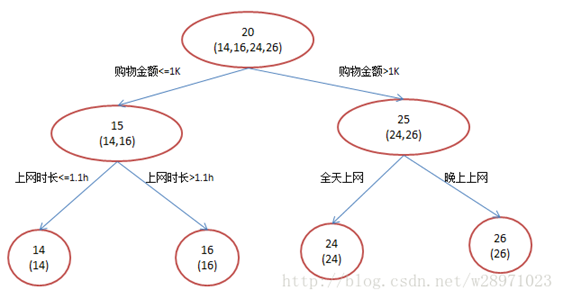
現在我們使用GBDT來訓練，由于數據太少，我們限定葉子節點最多有兩個，即每棵樹都只有一個分枝，并且限定只學兩棵樹。我們會得到如下圖2所示結果：

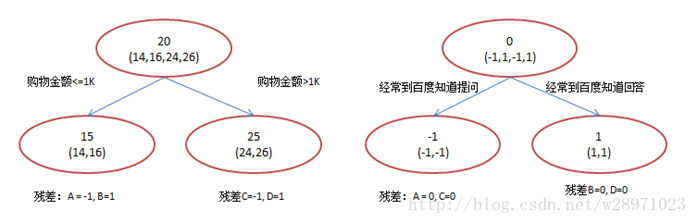
在第一棵樹分枝和圖1一樣，由于A,B年齡較為相近，C,D年齡較為相近，他們被分為兩撥，每撥用平均年齡作為預測值。A,B,C,D的殘差分別為-1,1，-1,1。然后我們拿殘差替代A,B,C,D的原值，到第二棵樹去學習，如果我們的預測值和它們的殘差相等，則只需把第二棵樹的結論累加到第一棵樹上就能得到真實年齡了。第二棵樹只有兩個值1和-1，直接分成兩個節點。此時所有人的殘差都是0，即每個人都得到了真實的預測值。

A: 14歲高一學生，購物較少，經常提問題；預測年齡A = 15 – 1 = 14
B: 16歲高三學生；購物較少，經常回答問題；預測年齡B = 15 + 1 = 16
C: 24歲應屆畢業生；購物較多，經常提問題；預測年齡C = 25 – 1 = 24
D: 26歲工作兩年員工；購物較多，經常回答問題；預測年齡D = 25 + 1 = 26

為什么要用梯度提升決策樹？
我們發現圖1為了達到100%精度使用了3個feature（上網時長、時段、網購金額），其中分枝“上網時長>1.1h” 很顯然已經過擬合了。用上網時間是不是>1.1小時來判斷所有人的年齡很顯然是有悖常識的；相對來說圖2的boosting雖然用了兩棵樹，但其實只用了2個feature就搞定了，后一個feature是問答比例，顯然圖2的依據更靠譜

Boosting的最大好處在于，每一步的殘差計算其實變相地增大了分錯instance的權重，而已經分對的instance則都趨向于0。這樣后面的樹就能越來越專注那些前面被分錯的instance。
那么哪里體現了Gradient呢？其實回到第一棵樹結束時，無論此時的cost function是什么，是均方差還是均差，只要它以誤差作為衡量標準，殘差向量(-1, 1, -1, 1)都是它的全局最優方向，這就是Gradient。

1.3 Shrinkage

Shrinkage(縮減)認為，每次走一小步逐步逼近的結果要比每次邁一大步逼近結果更加容易避免過擬合。即它不完全信任每一個棵殘差樹，它認為每棵樹只學到了真理的一小部分，累加的時候只累加一小部分，通過多學幾棵樹彌補不足。即

• 沒用Shrinkage時：（yi表示第i棵樹上y的預測值， y(1~i)表示前i棵樹y的綜合預測值）

y(i+1) = 殘差(y1~yi)， 其中： 殘差(y1~yi) =  y真實值 - y(1 ~ i)
y(1 ~ i) = SUM(y1, ..., yi)

• Shrinkage不改變第一個方程，只把第二個方程改為：

y(1 ~ i) = y(1 ~ i-1) + step * yi

即Shrinkage仍然以殘差作為學習目標，但對于殘差學習出來的結果，只累加一小部分（step*殘差）逐步逼近目標。step一般都比較小，如0.01~0.001（注意該step非gradient的step），導致各個樹的殘差是漸變的而不是陡變的。直覺上這也很好理解，不像直接用殘差一步修復誤差，而是只修復一點點，其實就是把大步切成了很多小步。

本質上，Shrinkage為每棵樹設置了一個weight，累加時要乘以這個weight，但和Gradient并沒有關系。這個weight就是step。就像Adaboost一樣，Shrinkage能減少過擬合發生也是經驗證明的，目前還沒有看到從理論的證明。

1.4 調參

• 樹的個數 100~10000
• 葉子的深度 3~8
• 學習速率 0.01~1
• 葉子上最大節點樹 20
• 訓練采樣比例 0.5~1
• 訓練特征采樣比例 sqrt(num)

1.5 GBDT的適用范圍

該版本GBDT幾乎可用于所有回歸問題（線性/非線性），相對logistic regression僅能用于線性回歸，GBDT的適用面非常廣。亦可用于二分類問題（設定閾值，大于閾值為正例，反之為負例）。

1.6 優缺點

(1) 優點：

• 精度高
• 能處理非線性數據
• 能處理多特征類型
• 適合低維稠密數據

(2) 缺點：

• 并行麻煩（因為上下兩顆樹有聯系）
• 多分類的時候 復雜度很大

二、XGBoost (eXtreme Gradient Boosting)

2.1 損失函數

XGBOOST預測函數可表示為：

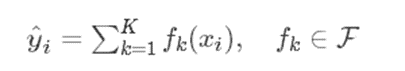
我們使用分部加法，可將此式變換為：

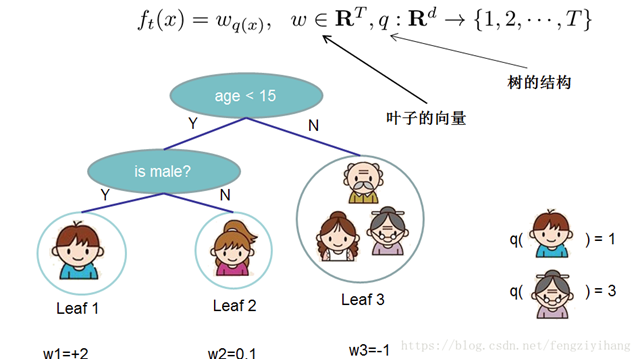
其中K代表迭代K輪，方程左側為預測值。映射fk如下(其中w為葉子節點的得分，q(xi)代表樣本值xi 通過函數q(xi)映射到某個葉子節點)：

目標函數：誤差函數+正則化

所以目標函數就可變化為：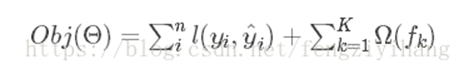
由前面的公式，我們知道：

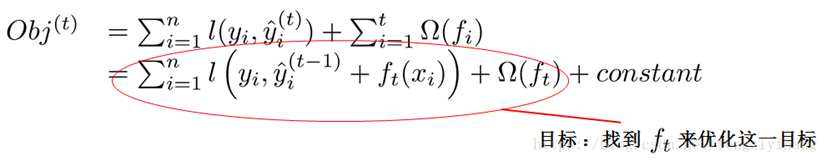
我們可以使用泰勒二階展開：

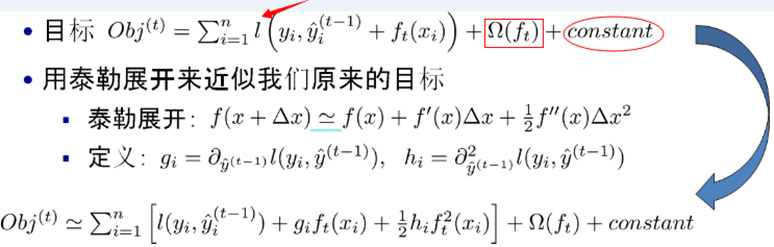
注：紅色箭頭指向的l為損失函數；紅色方框為正則項，包括L1、L2；紅色圓圈為常數項。xgboost利用泰勒展開做一個近似。最終的目標函數只依賴于每個數據點的在誤差函數上的一階導數和二階導數。

2.2 正則項

接下來我們使用L2構建正則化函數：

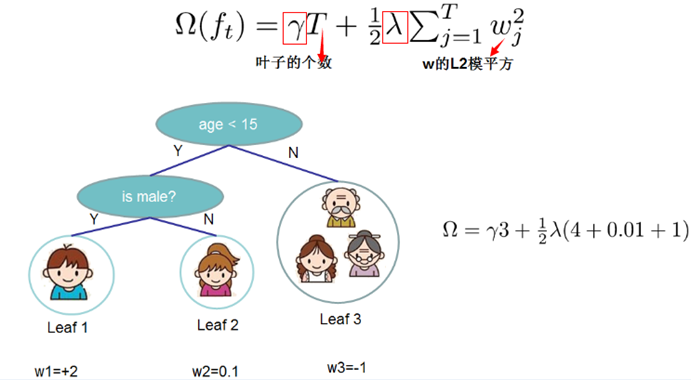
xgboost樹的復雜度包含了兩個部分：
(1) 葉子節點的個數T
(2) 葉子節點的得分w的L2正則（相當于針對每個葉結點的得分增加L2平滑，目的是為了避免過擬合）

考慮到正則項表達式為：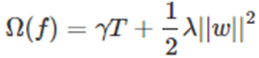

我們可以把之前的目標函數進行如下變形：

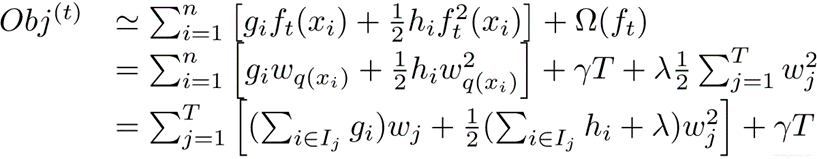
其中g是一階導數，h是二階導數。 $I_j$被定義為每個葉節點j上面樣本下標的集合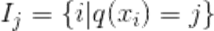 ，q(xi)要表達的是：每個樣本值xi 都能通過函數q(xi)映射到樹上的某個葉子節點，從而通過這個定義把兩種累加統一到了一起。

接著，我們可以定義：

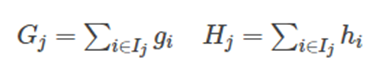
最終公式可以化簡為：

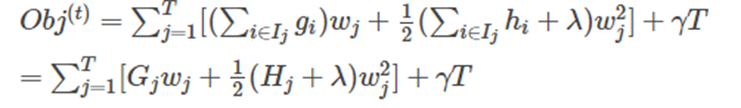
通過對 $w_j$ 求導等于0，可以得到：

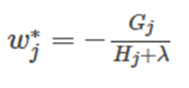
然后把 $w_j$ 最優解代入得到：

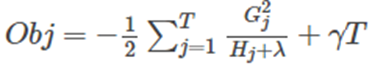
2.3 打分函數計算

Obj代表了當我們指定一個樹的結構的時候，我們在目標上面最多減少多少。我們可以把它叫做 結構分數(structure score)。結構分數值越小，代表這個樹的結構越好。

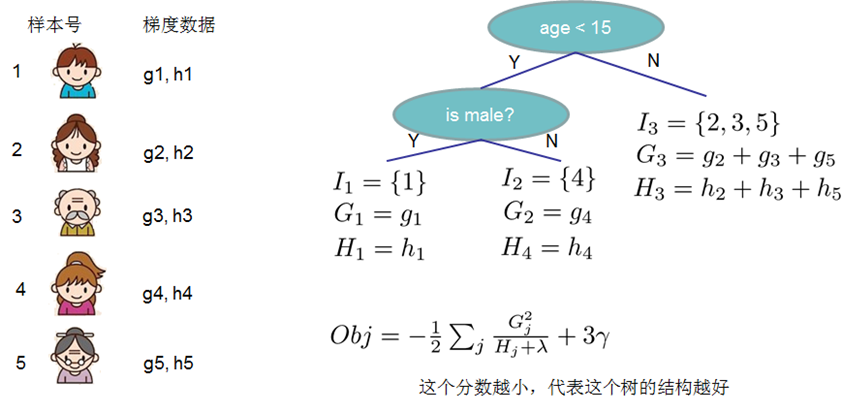
2.4 分裂節點

對于一個葉子節點如何進行分裂，xgboost作者在其原始論文中給出了兩種分裂節點的方法
（1） 枚舉所有不同樹結構的貪心法
不斷地枚舉不同樹的結構，然后利用打分函數來尋找出一個最優結構的樹，接著加入到模型中，不斷重復這樣的操作。利用枚舉法來得到最優樹結構集合，其結構很復雜，所以通常選擇貪心法。從樹深度0開始，每一節點都遍歷所有的特征，比如年齡、性別等等，然后對于某個特征，先按照該特征里的值進行排序，然后線性掃描該特征進而確定最好的分割點，最后對所有特征進行分割后，我們選擇所謂的增益Gain最高的那個特征。

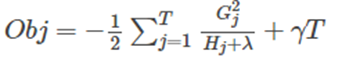
在之前求出的目標函數表達式中，G/(H+λ) 表示著每一個葉子節點對當前模型損失的貢獻程度，融合一下，得到Gain的計算表達式，如下所示：

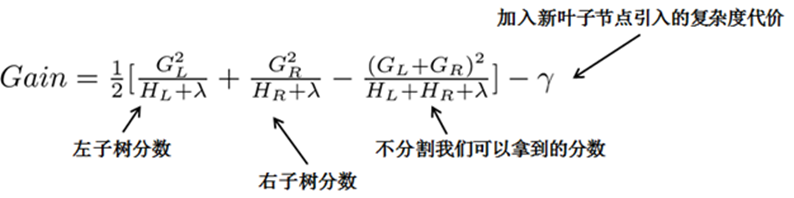
其中GL為原葉節點左兒子的誤差函數一階導數之和；GL為原葉節點右兒子的誤差函數一階導數之和。
例如分裂點a：

但由于又引進了一個新的量復雜度代價，所以增益衡量是否引進行的分裂還有一些問題，我們可以設置一個閥值，小于于閥值不引入新的分裂，大于閥值引入新的分裂。

2.5 算法過程

1. 不斷地進行特征分裂來生成一棵樹。每次添加一棵樹，其實是學習一個新函數，去擬合上次預測的殘差。
   

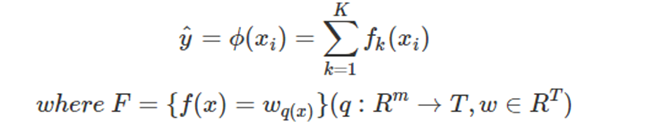
注：$W_{q(x)}$為葉子節點q的分數，對應了所有K棵回歸樹的集合，而f(x)為其中一棵回歸樹。

2. 當我們訓練完成得到k棵樹，我們要預測一個樣本的分數，其實就是根據這個樣本的特征，在每棵樹中會落到對應的一個葉子節點，每個葉子節點就對應一個分數。

3. 最后只需要將每棵樹對應的分數加起來就是該樣本的預測值。

2.6 參數詳解

(1) General Parameters（常規參數）

• booster [default=gbtree]：基分類器。gbtree: tree-based models; gblinear: linear models
• silent [default=0]:設置成1則沒有運行信息輸出，最好是設置為0.
• nthread [default to maximum number of threads available if not set]：線程數

(2) Booster Parameters（模型參數）

• eta [default=0.3]: shrinkage參數，用于更新葉子節點權重時，乘以該系數，避免步長過大。參數值越大，越可能無法收斂。把學習率eta設置得小一些，小學習率可以使得后面的學習更加仔細。
• min_child_weight [default=1]:這個參數默認是 1，是每個葉子里面h的和至少是多少，對正負樣本不均衡時的0-1分類而言，假設h 在0.01附近，min_child_weight為1 意味著葉子節點中最少需要包含100個樣本。這個參數非常影響結果，控制葉子節點中二階導的和的最小值，該參數值越小，越容易overfitting。
• max_depth [default=6]: 每顆樹的最大深度，樹高越深，越容易過擬合。
• max_leaf_nodes: 最大葉結點數，與max_depth作用有點重合。
• gamma [default=0]：后剪枝時，用于控制是否后剪枝的參數。
• max_delta_step [default=0]：這個參數在更新步驟中起作用，如果取0表示沒有約束，如果取正值則使得更新步驟更加保守。可以防止做太大的更新步子，使更新更加平緩。
• subsample [default=1]：樣本隨機采樣，較低的值使得算法更加保守，防止過擬合，但是太小的值也會造成欠擬合。
• colsample_bytree [default=1]：列采樣，對每棵樹的生成用的特征進行列采樣。一般設置為：0.5-1
• lambda [default=1]：控制模型復雜度的權重值的L2正則化項參數，參數越大，模型越不容易過擬合。
• alpha [default=0]:控制模型復雜程度的權重值的 L1 正則項參數，參數值越大，模型越不容易過擬合。
• scale_pos_weight [default=1]：如果取值大于0的話，在類別樣本不平衡的情況下有助于快速收斂。

(3) Learning Task Parameters（學習任務參數）

• objective [default=reg:linear]：定義最小化損失函數類型，常用參數：

  • binary: logistic – logistic regression for binary classification, returns predicted probability (not class)
  • multi: softmax – multiclass classification using the softmax objective, returns predicted class (not probabilities) . You also need to set an additional num_class (number of classes) parameter defining the number of unique classes
  • multi: softprob – same as softmax, but returns predicted probability of each data point belonging to each class.

• eval_metric [default according to objective]：The metric to be used for validation data.
  The default values are rmse for regression and error for classification. Typical values are:

  • rmse – root mean square error
  • mae – mean absolute error
  • logloss – negative log-likelihood
  • error – Binary classification error rate (0.5 threshold)
  • merror – Multiclass classification error rate
  • mlogloss – Multiclass logloss
  • auc: Area under the curve

• seed [default=0]：

  • The random number seed. 隨機種子，用于產生可復現的結果

2.7 XGBoost VS GBDT

(1) 傳統GBDT以CART作為基分類器，xgboost還支持線性分類器，這個時候xgboost相當于帶L1和L2正則化項的logistic回歸（分類問題）或者線性回歸（回歸問題）。

(2) 傳統GBDT在優化時只用到一階導數信息，xgboost則對代價函數進行了二階泰勒展開，同時用到了一階和二階導數。順便提一下，xgboost工具支持自定義代價函數，只要函數可一階和二階求導。

(3) xgboost在代價函數里加入了正則項，用于控制模型的復雜度。正則項里包含了樹的葉子節點個數、每個葉子節點上輸出的score的L2模的平方和。從Bias-variance tradeoff角度來講，正則項降低了模型的variance，使學習出來的模型更加簡單，防止過擬合，這也是xgboost優于傳統GBDT的一個特性。

(4) Shrinkage（縮減），相當于學習速率（xgboost中的eta）。xgboost在進行完一次迭代后，會將葉子節點的權重乘上該系數，主要是為了削弱每棵樹的影響，讓后面有更大的學習空間。實際應用中，一般把eta設置得小一點，然后迭代次數設置得大一點。（補充：傳統GBDT的實現也有學習速率）

(5) 列抽樣（column subsampling）。xgboost借鑒了隨機森林的做法，支持列抽樣，不僅能降低過擬合，還能減少計算，這也是xgboost異于傳統gbdt的一個特性。

(6) 對缺失值的處理。對于特征的值有缺失的樣本，xgboost可以自動學習出它的分裂方向。

(7) xgboost工具支持并行。boosting不是一種串行的結構嗎?怎么并行的？注意xgboost的并行不是tree粒度的并行，xgboost也是一次迭代完才能進行下一次迭代的（第t次迭代的代價函數里包含了前面t-1次迭代的預測值）。xgboost的并行是在特征粒度上的。我們知道，決策樹的學習最耗時的一個步驟就是對特征的值進行排序（因為要確定最佳分割點）。xgboost在訓練之前，預先對數據進行了排序，然后保存為block結構，后面的迭代中重復地使用這個結構，大大減小計算量。這個block結構也使得并行成為了可能。在進行節點的分裂時，需要計算每個特征的增益，最終選增益最大的那個特征去做分裂，那么各個特征的增益計算就可以開多線程進行。

(8) 可并行的近似直方圖算法。樹節點在進行分裂時，我們需要計算每個特征的每個分割點對應的增益，即用貪心法枚舉所有可能的分割點。當數據無法一次載入內存或者在分布式情況下，貪心算法效率就會變得很低，所以xgboost還提出了一種可并行的近似直方圖算法，用于高效地生成候選的分割點。

三、LightGBM

3.1 LightGBM原理

傳統的boosting算法（如GBDT和XGBoost）已經有相當好的效率，但在效率和可擴展性上不能滿足現在的需求，主要的原因就是傳統的boosting算法需要對每一個特征都要掃描所有的樣本點來選擇最好的切分點，這是非常的耗時。

為了解決這種在大樣本高維度數據的環境下耗時的問題，Lightgbm使用了如下兩種解決辦法：

• GOSS（Gradient-based One-Side Sampling, 基于梯度的單邊采樣）。不是使用所用的樣本點來計算梯度，而是對樣本進行采樣來計算梯度。
• EFB（Exclusive Feature Bundling， 互斥特征捆綁）。不是使用所有的特征來進行掃描獲得最佳的切分點，而是將某些特征進行捆綁在一起來降低特征的維度，使得尋找最佳切分點的消耗減少。
  這樣大大的降低的處理樣本的時間復雜度，但在精度上，通過大量的實驗證明，在某些數據集上使用Lightgbm并不損失精度，甚至有時還會提升精度。

3.2 Lightgbm的一些其它特性

(1) Leaf-wise的決策樹生長策略
大部分決策樹的學習算法通過 level-wise 策略生長樹，即一次分裂同一層的葉子，不加區分的對待同一層的葉子。而實際上很多葉子的分裂增益較低沒必要進行分裂，帶來了沒必要的開銷。如下圖：

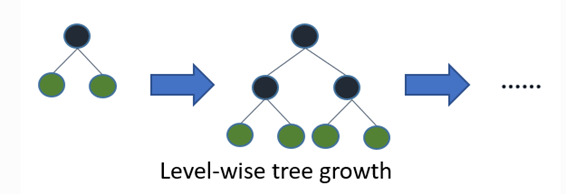
LightGBM 通過 leaf-wise 策略來生長樹。每次從當前所有葉子中，找到分裂增益最大的一個葉子，然后分裂，如此循環。因此同Level-wise相比，在分裂次數相同的情況下，Leaf-wise可以降低更多的誤差，得到更好的精度。但是，當樣本量較小的時候，leaf-wise 可能會造成過擬合。所以，LightGBM 可以利用額外的參數max_depth來限制樹的深度并避免過擬合。

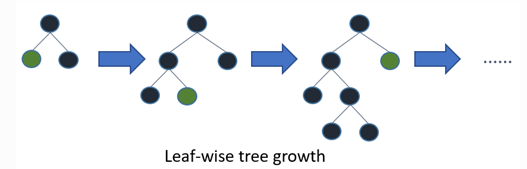
(2) 類別特征值的最優分割
對于類別型的數據，我們通常將類別特征轉化為one-hot編碼。 然而，對于學習樹來說這不是個好的解決方案。原因是，對于一個基數較大的類別特征，學習樹會生長的非常不平衡，并且需要非常深的深度才能來達到較好的準確率。

(3)Lightgbm中的并行學習

(3.1) 特征并行

傳統的特征并行算法: 旨在于在并行化決策樹中的尋找最佳切分點，主要流程如下：

• 垂直切分數據（不同的Worker有不同的特征集）；
• 在本地特征集尋找最佳切分點 {特征，閾值}；
• 在各個機器之間進行通信，拿出自己的最佳切分點，然后從所有的最佳切分點中推舉出一個最好的切分點，作為全局的切分點；
• 以最佳劃分方法對數據進行劃分，并將數據劃分結果傳遞給其他Worker；
• 其他Worker對接受到的數據進一步劃分。
  傳統的特征并行方法主要不足:
• 存在計算上的局限，傳統特征并行無法加速特征切分（時間復雜度為 ）。 因此，當數據量很大的時候，難以加速。
• 需要對劃分的結果進行通信整合，其額外的時間復雜度約為。（一個數據一個字節）

LightGBM中的特征并行: 不再垂直劃分數據，即每個Worker都持有全部數據。 因此，LighetGBM中沒有數據劃分結果之間通信的開銷，各個Worker都知道如何劃分數據。 而且，樣本量也不會變得更大，所以，使每個機器都持有全部數據是合理的。

LightGBM 中特征并行的流程如下：

• 每個Worker都在本地特征集上尋找最佳劃分點｛特征，閾值｝；
• 本地進行各個劃分的通信整合并得到最佳劃分；
• 執行最佳劃分。

然而，該特征并行算法在數據量很大時仍然存在計算上的局限。因此，建議在數據量很大時使用數據并行。

(3.2) 數據并行
傳統的數據并行算法：

• 水平劃分數據；
• Worker以本地數據構建本地直方圖；
• 將所有Worker的本地直方圖整合成全局整合圖；
• 在全局直方圖中尋找最佳切分，然后執行此切分。

傳統數據并行的不足：高通訊開銷。

LightGBM中的數據并行： 通過減少數據并行過程中的通訊開銷，來減少數據并行的開銷：

• 不同于傳統數據并行算法中的，整合所有本地直方圖以形成全局直方圖的方式，LightGBM 使用Reduce scatter的方式對不同Worker的不同特征（不重疊的）進行整合。 然后Worker從本地整合直方圖中尋找最佳劃分并同步到全局的最佳劃分中。
• 如上面提到的，LightGBM 通過直方圖做差法加速訓練。 基于此，我們可以進行單葉子的直方圖通訊，并且在相鄰直方圖上使用做差法。