代碼隨想錄算法訓練營第二十五天:樹的最后學習
如果不對遞歸有深刻的理解,本題有點難 單純移除一個節點那還不夠,要修剪!
#669. 修剪二叉搜索樹
力扣題目鏈接(opens new window)
給定一個二叉搜索樹,同時給定最小邊界L 和最大邊界 R。通過修剪二叉搜索樹,使得所有節點的值在[L, R]中 (R>=L) 。你可能需要改變樹的根節點,所以結果應當返回修剪好的二叉搜索樹的新的根節點。
? ?
?
? ?
?
#算法公開課
《代碼隨想錄》算法視頻公開課 ****(opens new window)****? :?你修剪的方式不對,我來給你糾正一下!| LeetCode:669. 修剪二叉搜索樹 ****(opens new window)****? ,相信結合視頻在看本篇題解,更有助于大家對本題的理解。
#思路
相信看到這道題目大家都感覺是一道簡單題(事實上leetcode上也標明是簡單)。
但還真的不簡單!
#遞歸法
直接想法就是:遞歸處理,然后遇到 root->val < low || root->val > high? 的時候直接return NULL,一波修改,趕緊利落。
不難寫出如下代碼:
class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
if (root == nullptr || root->val < low || root->val > high) return nullptr;
root->left = trimBST(root->left, low, high);
root->right = trimBST(root->right, low, high);
return root;
}
};
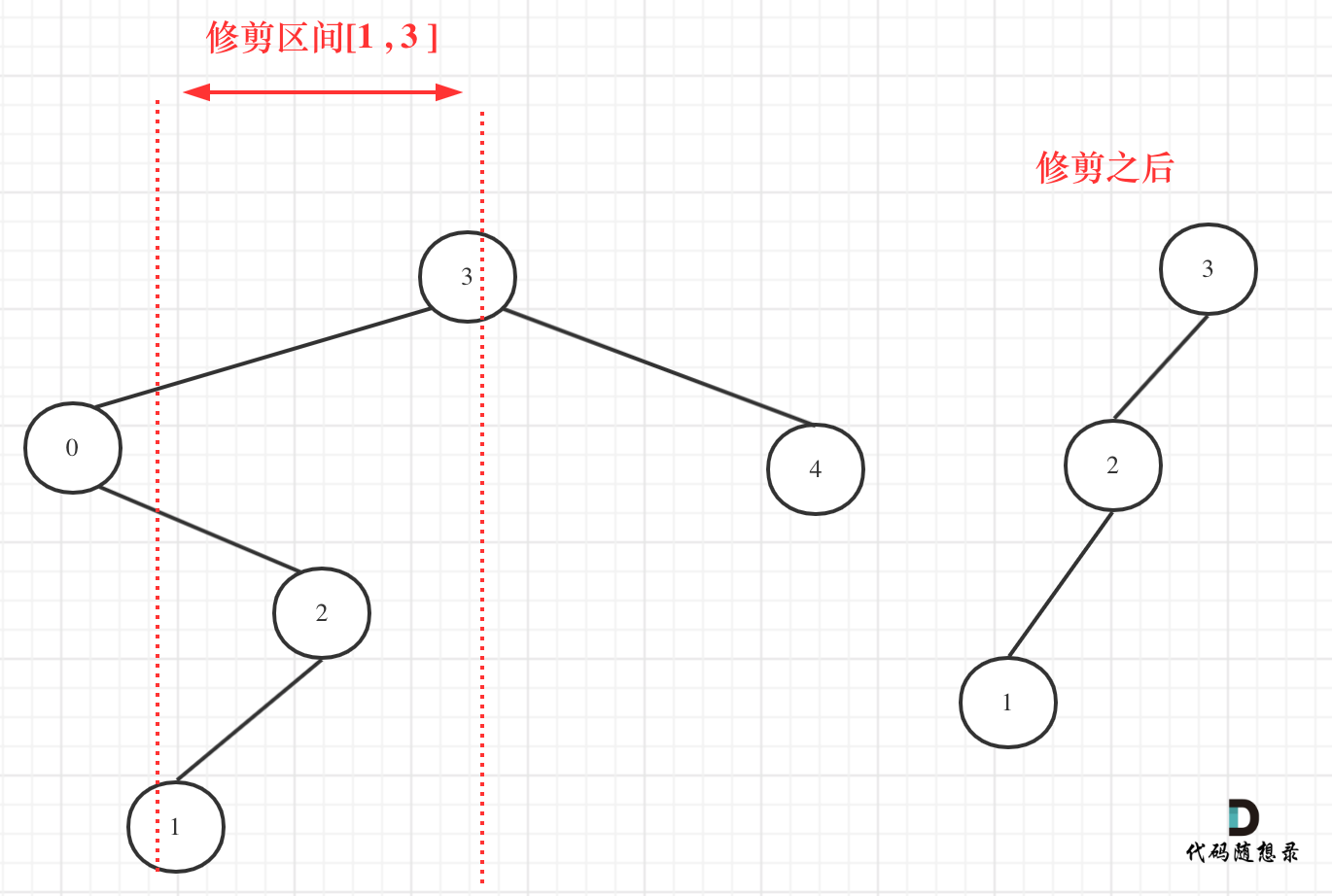
然而[1, 3]區間在二叉搜索樹的中可不是單純的節點3和左孩子節點0就決定的,還要考慮節點0的右子樹。
我們在重新關注一下第二個示例,如圖:
? ?
?
所以以上的代碼是不可行的!
從圖中可以看出需要重構二叉樹,想想是不是本題就有點復雜了。
其實不用重構那么復雜。
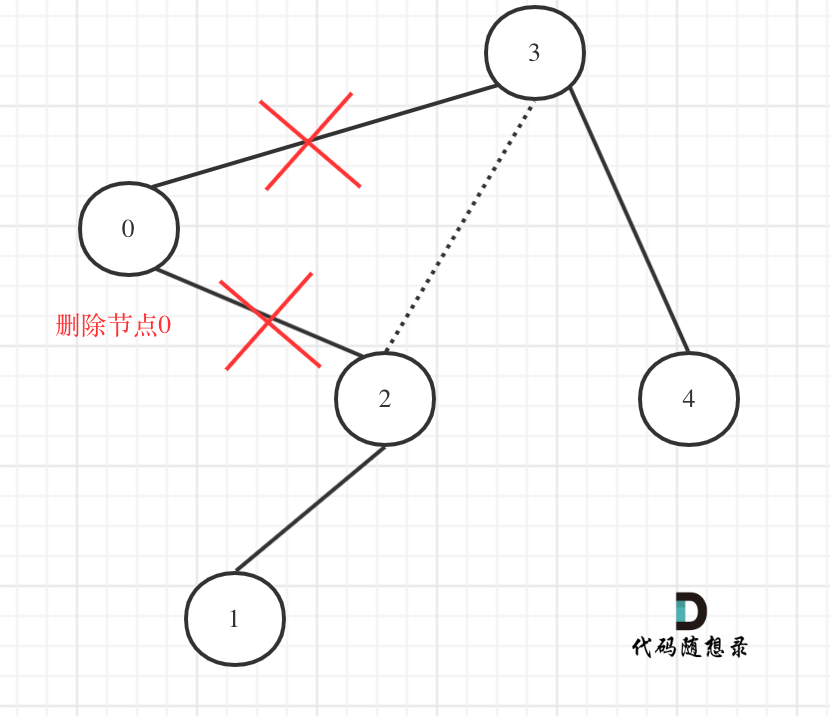
在上圖中我們發現節點0并不符合區間要求,那么將節點0的右孩子 節點2 直接賦給 節點3的左孩子就可以了(就是把節點0從二叉樹中移除),如圖:
? ?
?
理解了最關鍵部分了我們再遞歸三部曲:
- 確定遞歸函數的參數以及返回值
這里我們為什么需要返回值呢?
因為是要遍歷整棵樹,做修改,其實不需要返回值也可以,我們也可以完成修剪(其實就是從二叉樹中移除節點)的操作。
但是有返回值,更方便,可以通過遞歸函數的返回值來移除節點。
這樣的做法在二叉樹:搜索樹中的插入操作 ?**(opens new window)** 和二叉樹:搜索樹中的刪除操作 ?**(opens new window)** 中大家已經了解過了。
代碼如下:
TreeNode* trimBST(TreeNode* root, int low, int high)
- 確定終止條件
修剪的操作并不是在終止條件上進行的,所以就是遇到空節點返回就可以了。
if (root == nullptr ) return nullptr;
- 確定單層遞歸的邏輯
如果root(當前節點)的元素小于low的數值,那么應該遞歸右子樹,并返回右子樹符合條件的頭結點。
代碼如下:
if (root->val < low) {
TreeNode* right = trimBST(root->right, low, high); // 尋找符合區間[low, high]的節點
return right;
}
如果root(當前節點)的元素大于high的,那么應該遞歸左子樹,并返回左子樹符合條件的頭結點。
代碼如下:
if (root->val > high) {
TreeNode* left = trimBST(root->left, low, high); // 尋找符合區間[low, high]的節點
return left;
}
接下來要將下一層處理完左子樹的結果賦給root->left,處理完右子樹的結果賦給root->right。
最后返回root節點,代碼如下:
root->left = trimBST(root->left, low, high); // root->left接入符合條件的左孩子
root->right = trimBST(root->right, low, high); // root->right接入符合條件的右孩子
return root;
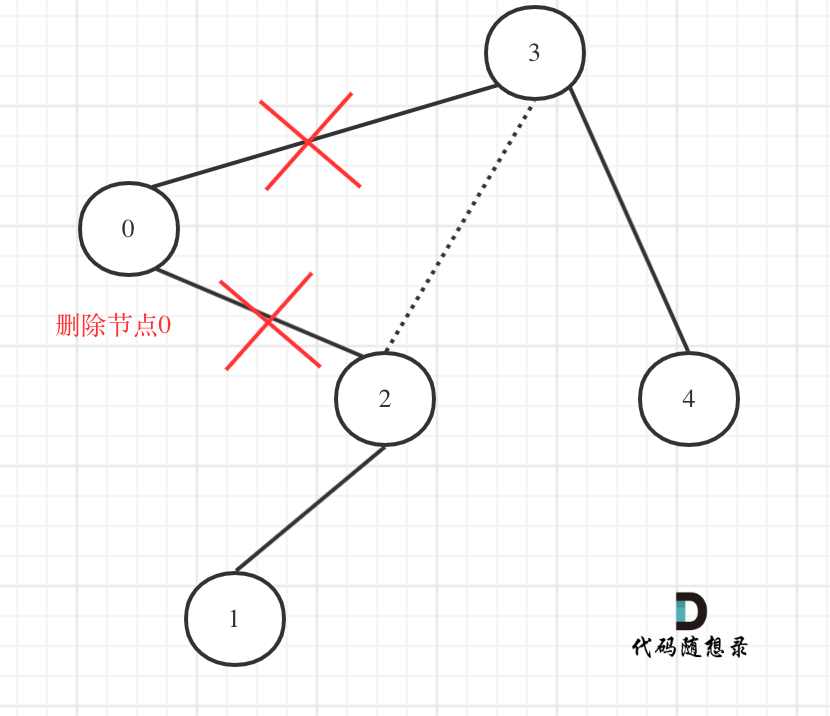
此時大家是不是還沒發現這多余的節點究竟是如何從二叉樹中移除的呢?
在回顧一下上面的代碼,針對下圖中二叉樹的情況:
? ?
?
如下代碼相當于把節點0的右孩子(節點2)返回給上一層,
if (root->val < low) {
TreeNode* right = trimBST(root->right, low, high); // 尋找符合區間[low, high]的節點
return right;
}
然后如下代碼相當于用節點3的左孩子 把下一層返回的 節點0的右孩子(節點2) 接住。
root->left = trimBST(root->left, low, high);
此時節點3的左孩子就變成了節點2,將節點0從二叉樹中移除了。
最后整體代碼如下:
class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
if (root == nullptr ) return nullptr;
if (root->val < low) {
TreeNode* right = trimBST(root->right, low, high); // 尋找符合區間[low, high]的節點
return right;
}
if (root->val > high) {
TreeNode* left = trimBST(root->left, low, high); // 尋找符合區間[low, high]的節點
return left;
}
root->left = trimBST(root->left, low, high); // root->left接入符合條件的左孩子
root->right = trimBST(root->right, low, high); // root->right接入符合條件的右孩子
return root;
}
};
精簡之后代碼如下:
class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
if (root == nullptr) return nullptr;
if (root->val < low) return trimBST(root->right, low, high);
if (root->val > high) return trimBST(root->left, low, high);
root->left = trimBST(root->left, low, high);
root->right = trimBST(root->right, low, high);
return root;
}
};
只看代碼,其實不太好理解節點是如何移除的,這一塊大家可以自己再模擬模擬!
#迭代法
因為二叉搜索樹的有序性,不需要使用棧模擬遞歸的過程。
在剪枝的時候,可以分為三步:
- 將root移動到[L, R] 范圍內,注意是左閉右閉區間
- 剪枝左子樹
- 剪枝右子樹
代碼如下:
class Solution {
public:
TreeNode* trimBST(TreeNode* root, int L, int R) {
if (!root) return nullptr;// 處理頭結點,讓root移動到[L, R] 范圍內,注意是左閉右閉
while (root != nullptr && (root->val < L || root->val > R)) {
if (root->val < L) root = root->right; // 小于L往右走
else root = root->left; // 大于R往左走
}
TreeNode *cur = root;
// 此時root已經在[L, R] 范圍內,處理左孩子元素小于L的情況
while (cur != nullptr) {
while (cur->left && cur->left->val < L) {
cur->left = cur->left->right;
}
cur = cur->left;
}
cur = root;// 此時root已經在[L, R] 范圍內,處理右孩子大于R的情況
while (cur != nullptr) {
while (cur->right && cur->right->val > R) {
cur->right = cur->right->left;
}
cur = cur->right;
}
return root;
}
};
#總結
修剪二叉搜索樹其實并不難,但在遞歸法中大家可看出我費了很大的功夫來講解如何刪除節點的,這個思路其實是比較繞的。
最終的代碼倒是很簡潔。
如果不對遞歸有深刻的理解,這道題目還是有難度的!
本題我依然給出遞歸法和迭代法,初學者掌握遞歸就可以了,如果想進一步學習,就把迭代法也寫一寫。
構造二叉搜索樹,一不小心就平衡了
#108.將有序數組轉換為二叉搜索樹
力扣題目鏈接(opens new window)
將一個按照升序排列的有序數組,轉換為一棵高度平衡二叉搜索樹。
本題中,一個高度平衡二叉樹是指一個二叉樹每個節點 的左右兩個子樹的高度差的絕對值不超過 1。
示例:
? ?
?
#算法公開課
《代碼隨想錄》算法視頻公開課 ****(opens new window)****? :?構造平衡二叉搜索樹!| LeetCode:108.將有序數組轉換為二叉搜索樹 ****(opens new window)****? ,相信結合視頻在看本篇題解,更有助于大家對本題的理解。
#思路
做這道題目之前大家可以了解一下這幾道:
- 106.從中序與后序遍歷序列構造二叉樹(opens new window)
- 654.最大二叉樹 ?**(opens new window)** 中其實已經講過了,如果根據數組構造一棵二叉樹。
- 701.二叉搜索樹中的插入操作(opens new window)
- 450.刪除二叉搜索樹中的節點(opens new window)
進入正題:
題目中說要轉換為一棵高度平衡二叉搜索樹。為什么強調要平衡呢?
因為只要給我們一個有序數組,如果不強調平衡,都可以以線性結構來構造二叉搜索樹。
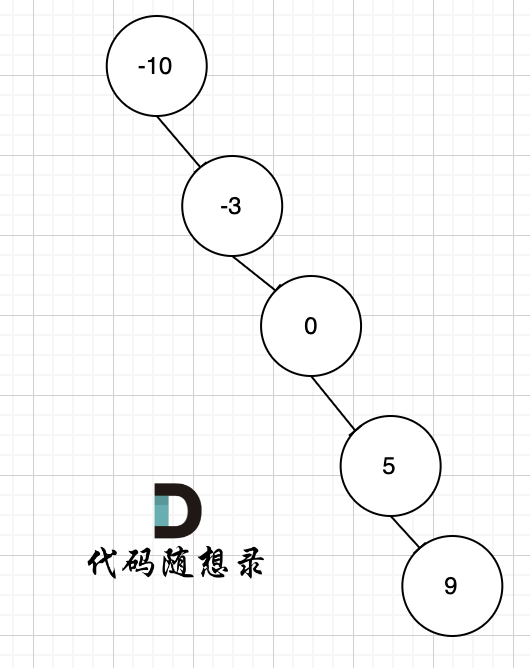
例如 有序數組[-10,-3,0,5,9] 就可以構造成這樣的二叉搜索樹,如圖。
? ?
?
上圖中,是符合二叉搜索樹的特性吧,如果要這么做的話,是不是本題意義就不大了,所以才強調是平衡二叉搜索樹。
其實數組構造二叉樹,構成平衡樹是自然而然的事情,因為大家默認都是從數組中間位置取值作為節點元素,一般不會隨機取。所以想構成不平衡的二叉樹是自找麻煩。
在二叉樹:構造二叉樹登場! ?**(opens new window)** 和二叉樹:構造一棵最大的二叉樹 ?**(opens new window)** 中其實已經講過了,如果根據數組構造一棵二叉樹。
本質就是尋找分割點,分割點作為當前節點,然后遞歸左區間和右區間。
本題其實要比二叉樹:構造二叉樹登場! ?**(opens new window)** 和 二叉樹:構造一棵最大的二叉樹 ?**(opens new window)** 簡單一些,因為有序數組構造二叉搜索樹,尋找分割點就比較容易了。
分割點就是數組中間位置的節點。
那么為問題來了,如果數組長度為偶數,中間節點有兩個,取哪一個?
取哪一個都可以,只不過構成了不同的平衡二叉搜索樹。
例如:輸入:[-10,-3,0,5,9]
如下兩棵樹,都是這個數組的平衡二叉搜索樹:
?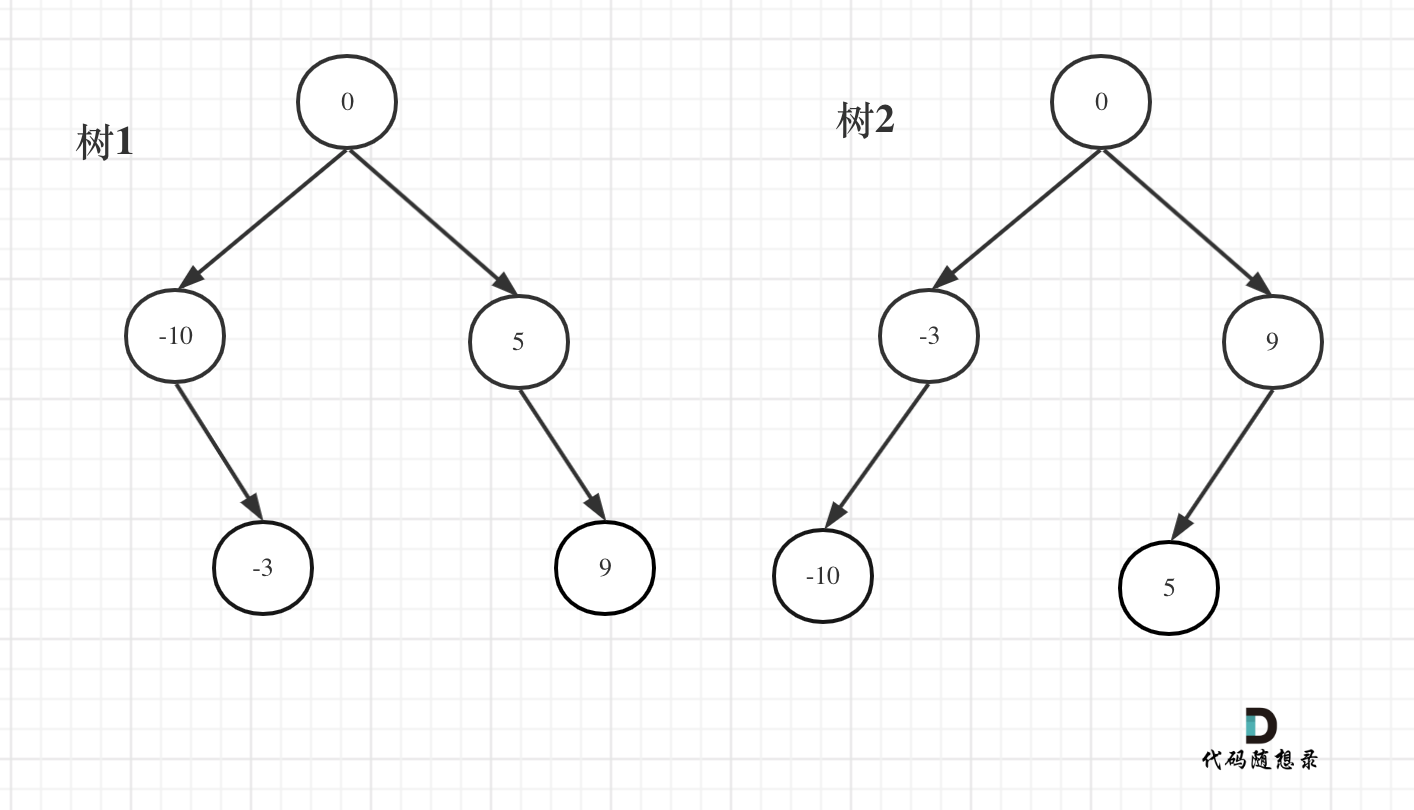 ?
?
如果要分割的數組長度為偶數的時候,中間元素為兩個,是取左邊元素 就是樹1,取右邊元素就是樹2。
這也是題目中強調答案不是唯一的原因。 理解這一點,這道題目算是理解到位了。
#遞歸
遞歸三部曲:
- 確定遞歸函數返回值及其參數
刪除二叉樹節點,增加二叉樹節點,都是用遞歸函數的返回值來完成,這樣是比較方便的。
相信大家如果仔細看了二叉樹:搜索樹中的插入操作 ?**(opens new window)** 和二叉樹:搜索樹中的刪除操作 ?**(opens new window)** ,一定會對遞歸函數返回值的作用深有感觸。
那么本題要構造二叉樹,依然用遞歸函數的返回值來構造中節點的左右孩子。
再來看參數,首先是傳入數組,然后就是左下標left和右下標right,我們在二叉樹:構造二叉樹登場! ?**(opens new window)** 中提過,在構造二叉樹的時候盡量不要重新定義左右區間數組,而是用下標來操作原數組。
所以代碼如下:
// 左閉右閉區間[left, right]
TreeNode* traversal(vector<int>& nums, int left, int right)
這里注意,我這里定義的是左閉右閉區間,在不斷分割的過程中,也會堅持左閉右閉的區間,這又涉及到我們講過的循環不變量。
在二叉樹:構造二叉樹登場! ?**(opens new window)** ,35.搜索插入位置 ?**(opens new window)** 和59.螺旋矩陣II ?**(opens new window)** 都詳細講過循環不變量。
- 確定遞歸終止條件
這里定義的是左閉右閉的區間,所以當區間 left > right的時候,就是空節點了。
代碼如下:
if (left > right) return nullptr;
- 確定單層遞歸的邏輯
首先取數組中間元素的位置,不難寫出int mid = (left + right) / 2;?,這么寫其實有一個問題,就是數值越界,例如left和right都是最大int,這么操作就越界了,在?**二分法** ****(opens new window)****?中尤其需要注意!
所以可以這么寫:int mid = left + ((right - left) / 2);?
但本題leetcode的測試數據并不會越界,所以怎么寫都可以。但需要有這個意識!
取了中間位置,就開始以中間位置的元素構造節點,代碼:TreeNode* root = new TreeNode(nums[mid]);?。
接著劃分區間,root的左孩子接住下一層左區間的構造節點,右孩子接住下一層右區間構造的節點。
最后返回root節點,單層遞歸整體代碼如下:
int mid = left + ((right - left) / 2);
TreeNode* root = new TreeNode(nums[mid]);
root->left = traversal(nums, left, mid - 1);
root->right = traversal(nums, mid + 1, right);
return root;
這里int mid = left + ((right - left) / 2);?的寫法相當于是如果數組長度為偶數,中間位置有兩個元素,取靠左邊的。
- 遞歸整體代碼如下:
class Solution {
private:
TreeNode* traversal(vector<int>& nums, int left, int right) {
if (left > right) return nullptr;
int mid = left + ((right - left) / 2);
TreeNode* root = new TreeNode(nums[mid]);
root->left = traversal(nums, left, mid - 1);
root->right = traversal(nums, mid + 1, right);
return root;
}
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
TreeNode* root = traversal(nums, 0, nums.size() - 1);
return root;
}
};
注意:在調用traversal的時候傳入的left和right為什么是0和nums.size() - 1,因為定義的區間為左閉右閉。
#迭代法
迭代法可以通過三個隊列來模擬,一個隊列放遍歷的節點,一個隊列放左區間下標,一個隊列放右區間下標。
模擬的就是不斷分割的過程,C++代碼如下:(我已經詳細注釋)
class Solution {
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
if (nums.size() == 0) return nullptr;TreeNode* root = new TreeNode(0); // 初始根節點
queue<TreeNode*> nodeQue; // 放遍歷的節點
queue<int> leftQue; // 保存左區間下標
queue<int> rightQue; // 保存右區間下標
nodeQue.push(root); // 根節點入隊列
leftQue.push(0); // 0為左區間下標初始位置
rightQue.push(nums.size() - 1); // nums.size() - 1為右區間下標初始位置while (!nodeQue.empty()) {
TreeNode* curNode = nodeQue.front();
nodeQue.pop();
int left = leftQue.front(); leftQue.pop();
int right = rightQue.front(); rightQue.pop();
int mid = left + ((right - left) / 2);curNode->val = nums[mid]; // 將mid對應的元素給中間節點if (left <= mid - 1) { // 處理左區間
curNode->left = new TreeNode(0);
nodeQue.push(curNode->left);
leftQue.push(left);
rightQue.push(mid - 1);
}if (right >= mid + 1) { // 處理右區間
curNode->right = new TreeNode(0);
nodeQue.push(curNode->right);
leftQue.push(mid + 1);
rightQue.push(right);
}
}
return root;
}
};
#總結
在?**二叉樹:構造二叉樹登場!** ****(opens new window)****?和 二叉樹:構造一棵最大的二叉樹 ****(opens new window)****?之后,我們順理成章的應該構造一下二叉搜索樹了,一不小心還是一棵平衡二叉搜索樹。
其實思路也是一樣的,不斷中間分割,然后遞歸處理左區間,右區間,也可以說是分治。
此時相信大家應該對通過遞歸函數的返回值來增刪二叉樹很熟悉了,這也是常規操作。
在定義區間的過程中我們又一次強調了循環不變量的重要性。
最后依然給出迭代的方法,其實就是模擬取中間元素,然后不斷分割去構造二叉樹的過程。
538.把二叉搜索樹轉換為累加樹
力扣題目鏈接(opens new window)
給出二叉 搜索 樹的根節點,該樹的節點值各不相同,請你將其轉換為累加樹(Greater Sum Tree),使每個節點 node 的新值等于原樹中大于或等于 node.val 的值之和。
提醒一下,二叉搜索樹滿足下列約束條件:
節點的左子樹僅包含鍵 小于 節點鍵的節點。 節點的右子樹僅包含鍵 大于 節點鍵的節點。 左右子樹也必須是二叉搜索樹。
示例 1:
?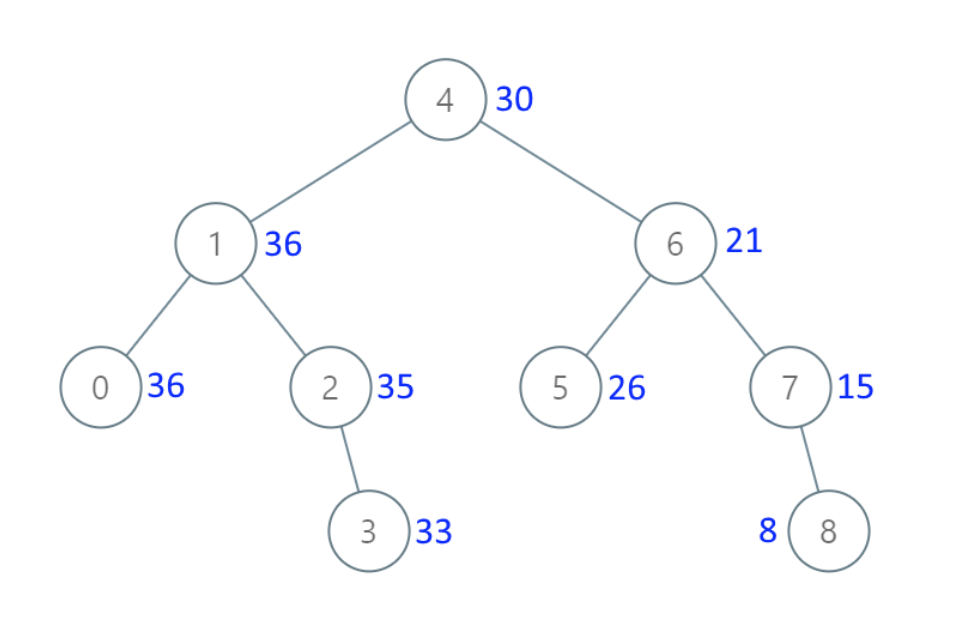 ?
?
- 輸入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
- 輸出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
- 輸入:root = [0,null,1]
- 輸出:[1,null,1]
示例 3:
- 輸入:root = [1,0,2]
- 輸出:[3,3,2]
示例 4:
- 輸入:root = [3,2,4,1]
- 輸出:[7,9,4,10]
提示:
- 樹中的節點數介于 0 和 104 之間。
- 每個節點的值介于 -104 和 104 之間。
- 樹中的所有值 互不相同 。
- 給定的樹為二叉搜索樹。
#算法公開課
《代碼隨想錄》算法視頻公開課 ****(opens new window)****? :?普大喜奔!二叉樹章節已全部更完啦!| LeetCode:538.把二叉搜索樹轉換為累加樹 ****(opens new window)****? ,相信結合視頻在看本篇題解,更有助于大家對本題的理解。
#思路
一看到累加樹,相信很多小伙伴都會疑惑:如何累加?遇到一個節點,然后再遍歷其他節點累加?怎么一想這么麻煩呢。
然后再發現這是一棵二叉搜索樹,二叉搜索樹啊,這是有序的啊。
那么有序的元素如何求累加呢?
其實這就是一棵樹,大家可能看起來有點別扭,換一個角度來看,這就是一個有序數組[2, 5, 13],求從后到前的累加數組,也就是[20, 18, 13],是不是感覺這就簡單了。
為什么變成數組就是感覺簡單了呢?
因為數組大家都知道怎么遍歷啊,從后向前,挨個累加就完事了,這換成了二叉搜索樹,看起來就別扭了一些是不是。
那么知道如何遍歷這個二叉樹,也就迎刃而解了,從樹中可以看出累加的順序是右中左,所以我們需要反中序遍歷這個二叉樹,然后順序累加就可以了。
#遞歸
遍歷順序如圖所示:
?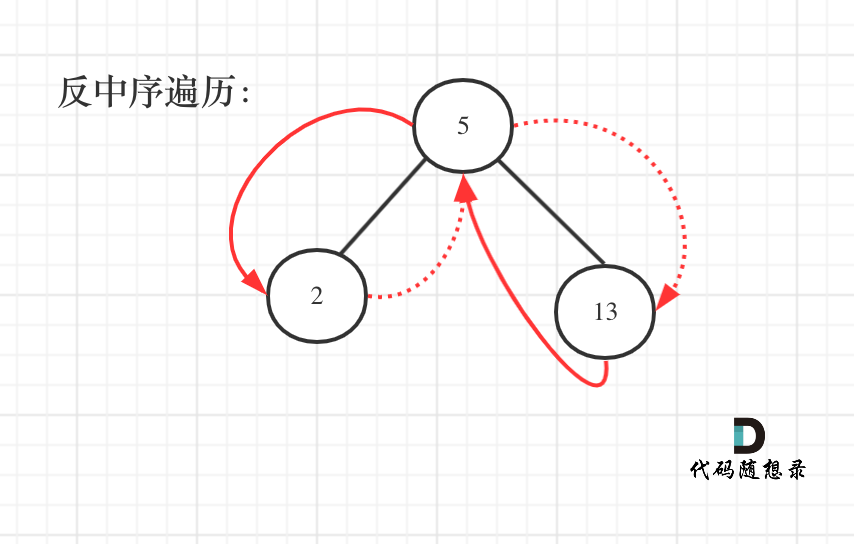 ?
?
本題依然需要一個pre指針記錄當前遍歷節點cur的前一個節點,這樣才方便做累加。
pre指針的使用技巧,我們在二叉樹:搜索樹的最小絕對差 ?**(opens new window)** 和二叉樹:我的眾數是多少? ?**(opens new window)** 都提到了,這是常用的操作手段。
- 遞歸函數參數以及返回值
這里很明確了,不需要遞歸函數的返回值做什么操作了,要遍歷整棵樹。
同時需要定義一個全局變量pre,用來保存cur節點的前一個節點的數值,定義為int型就可以了。
代碼如下:
int pre = 0; // 記錄前一個節點的數值
void traversal(TreeNode* cur)
- 確定終止條件
遇空就終止。
if (cur == NULL) return;
- 確定單層遞歸的邏輯
注意要右中左來遍歷二叉樹, 中節點的處理邏輯就是讓cur的數值加上前一個節點的數值。
代碼如下:
traversal(cur->right); // 右
cur->val += pre; // 中
pre = cur->val;
traversal(cur->left); // 左
遞歸法整體代碼如下:
class Solution {
private:
int pre = 0; // 記錄前一個節點的數值
void traversal(TreeNode* cur) { // 右中左遍歷
if (cur == NULL) return;
traversal(cur->right);
cur->val += pre;
pre = cur->val;
traversal(cur->left);
}
public:
TreeNode* convertBST(TreeNode* root) {
pre = 0;
traversal(root);
return root;
}
};
#迭代法
迭代法其實就是中序模板題了,在二叉樹:前中后序迭代法 ?**(opens new window)** 和二叉樹:前中后序統一方式迭代法 ?**(opens new window)** 可以選一種自己習慣的寫法。
這里我給出其中的一種,代碼如下:
class Solution {
private:
int pre; // 記錄前一個節點的數值
void traversal(TreeNode* root) {
stack<TreeNode*> st;
TreeNode* cur = root;
while (cur != NULL || !st.empty()) {
if (cur != NULL) {
st.push(cur);
cur = cur->right; // 右
} else {
cur = st.top(); // 中
st.pop();
cur->val += pre;
pre = cur->val;
cur = cur->left; // 左
}
}
}
public:
TreeNode* convertBST(TreeNode* root) {
pre = 0;
traversal(root);
return root;
}
};
Morris 遍歷
思路及算法
有一種巧妙的方法可以在線性時間內,只占用常數空間來實現中序遍歷。這種方法由 J. H. Morris 在 1979 年的論文「Traversing Binary Trees Simply and Cheaply」中首次提出,因此被稱為 Morris 遍歷。
Morris 遍歷的核心思想是利用樹的大量空閑指針,實現空間開銷的極限縮減。其反序中序遍歷規則總結如下:
如果當前節點的右子節點為空,處理當前節點,并遍歷當前節點的左子節點;
如果當前節點的右子節點不為空,找到當前節點右子樹的最左節點(該節點為當前節點中序遍歷的前驅節點);
如果最左節點的左指針為空,將最左節點的左指針指向當前節點,遍歷當前節點的右子節點;
如果最左節點的左指針不為空,將最左節點的左指針重新置為空(恢復樹的原狀),處理當前節點,并將當前節點置為其左節點;
重復步驟 1 和步驟 2,直到遍歷結束。
這樣我們利用 Morris 遍歷的方法,反序中序遍歷該二叉搜索樹,即可實現線性時間與常數空間的遍歷。
代碼
C++
class Solution {
public:TreeNode* getSuccessor(TreeNode* node) {TreeNode* succ = node->right;while (succ->left != nullptr && succ->left != node) {succ = succ->left;}return succ;}TreeNode* convertBST(TreeNode* root) {int sum = 0;TreeNode* node = root;while (node != nullptr) {if (node->right == nullptr) {sum += node->val;node->val = sum;node = node->left;} else {TreeNode* succ = getSuccessor(node);if (succ->left == nullptr) {succ->left = node;node = node->right;} else {succ->left = nullptr;sum += node->val;node->val = sum;node = node->left;}}}return root;}
};
·· TreeNode* convertBST(TreeNode* root) {
int sum = 0;
TreeNode* node = root;
二叉樹:總結篇!(需要掌握的二叉樹技能都在這里了)
力扣二叉樹大總結!
不知不覺二叉樹已經和我們度過了三十三天,「代碼隨想錄」 ?**(opens new window)** 里已經發了三十三篇二叉樹的文章,詳細講解了30+二叉樹經典題目,一直堅持下來的錄友們一定會二叉樹有深刻理解了。
在每一道二叉樹的題目中,我都使用了遞歸三部曲來分析題目,相信大家以后看到二叉樹,看到遞歸,都會想:返回值、參數是什么?終止條件是什么?單層邏輯是什么?
而且幾乎每一道題目我都給出對應的迭代法,可以用來進一步提高自己。
下面Carl把分析過的題目分門別類,可以幫助新錄友循序漸進學習二叉樹,也方便老錄友面試前快速復習,看到一個標題,就回想一下對應的解題思路,這樣很快就可以系統性的復習一遍二叉樹了。
公眾號的發文順序,就是循序漸進的,所以如下分類基本就是按照文章發文順序來的,我再做一個系統性的分類。
#二叉樹的理論基礎
- 關于二叉樹,你該了解這些! ?**(opens new window)** :二叉樹的種類、存儲方式、遍歷方式、定義方式
#二叉樹的遍歷方式
-
深度優先遍歷
- 二叉樹:前中后序遞歸法 ?**(opens new window)** :遞歸三部曲初次亮相
- 二叉樹:前中后序迭代法(一) ?**(opens new window)** :通過棧模擬遞歸
- 二叉樹:前中后序迭代法(二)統一風格(opens new window)
-
廣度優先遍歷
- 二叉樹的層序遍歷 ?**(opens new window)** :通過隊列模擬
#求二叉樹的屬性
-
二叉樹:是否對稱(opens new window)
- 遞歸:后序,比較的是根節點的左子樹與右子樹是不是相互翻轉
- 迭代:使用隊列/棧將兩個節點順序放入容器中進行比較
-
二叉樹:求最大深度(opens new window)
- 遞歸:后序,求根節點最大高度就是最大深度,通過遞歸函數的返回值做計算樹的高度
- 迭代:層序遍歷
-
二叉樹:求最小深度(opens new window)
- 遞歸:后序,求根節點最小高度就是最小深度,注意最小深度的定義
- 迭代:層序遍歷
-
二叉樹:求有多少個節點(opens new window)
- 遞歸:后序,通過遞歸函數的返回值計算節點數量
- 迭代:層序遍歷
-
二叉樹:是否平衡(opens new window)
- 遞歸:后序,注意后序求高度和前序求深度,遞歸過程判斷高度差
- 迭代:效率很低,不推薦
-
二叉樹:找所有路徑(opens new window)
- 遞歸:前序,方便讓父節點指向子節點,涉及回溯處理根節點到葉子的所有路徑
- 迭代:一個棧模擬遞歸,一個棧來存放對應的遍歷路徑
-
二叉樹:遞歸中如何隱藏著回溯(opens new window)
- 詳解二叉樹:找所有路徑 ?**(opens new window)** 中遞歸如何隱藏著回溯
-
二叉樹:求左葉子之和(opens new window)
- 遞歸:后序,必須三層約束條件,才能判斷是否是左葉子。
- 迭代:直接模擬后序遍歷
-
二叉樹:求左下角的值(opens new window)
- 遞歸:順序無所謂,優先左孩子搜索,同時找深度最大的葉子節點。
- 迭代:層序遍歷找最后一行最左邊
-
二叉樹:求路徑總和(opens new window)
- 遞歸:順序無所謂,遞歸函數返回值為bool類型是為了搜索一條邊,沒有返回值是搜索整棵樹。
- 迭代:棧里元素不僅要記錄節點指針,還要記錄從頭結點到該節點的路徑數值總和
#二叉樹的修改與構造
-
翻轉二叉樹(opens new window)
- 遞歸:前序,交換左右孩子
- 迭代:直接模擬前序遍歷
-
構造二叉樹(opens new window)
- 遞歸:前序,重點在于找分割點,分左右區間構造
- 迭代:比較復雜,意義不大
-
構造最大的二叉樹(opens new window)
- 遞歸:前序,分割點為數組最大值,分左右區間構造
- 迭代:比較復雜,意義不大
-
合并兩個二叉樹(opens new window)
- 遞歸:前序,同時操作兩個樹的節點,注意合并的規則
- 迭代:使用隊列,類似層序遍歷
#求二叉搜索樹的屬性
-
二叉搜索樹中的搜索(opens new window)
- 遞歸:二叉搜索樹的遞歸是有方向的
- 迭代:因為有方向,所以迭代法很簡單
-
是不是二叉搜索樹(opens new window)
- 遞歸:中序,相當于變成了判斷一個序列是不是遞增的
- 迭代:模擬中序,邏輯相同
-
求二叉搜索樹的最小絕對差(opens new window)
- 遞歸:中序,雙指針操作
- 迭代:模擬中序,邏輯相同
-
求二叉搜索樹的眾數(opens new window)
- 遞歸:中序,清空結果集的技巧,遍歷一遍便可求眾數集合
- 二叉搜索樹轉成累加樹(opens new window)
- 遞歸:中序,雙指針操作累加
- 迭代:模擬中序,邏輯相同
#二叉樹公共祖先問題
-
二叉樹的公共祖先問題(opens new window)
- 遞歸:后序,回溯,找到左子樹出現目標值,右子樹節點目標值的節點。
- 迭代:不適合模擬回溯
-
二叉搜索樹的公共祖先問題(opens new window)
- 遞歸:順序無所謂,如果節點的數值在目標區間就是最近公共祖先
- 迭代:按序遍歷
#二叉搜索樹的修改與構造
-
二叉搜索樹中的插入操作(opens new window)
- 遞歸:順序無所謂,通過遞歸函數返回值添加節點
- 迭代:按序遍歷,需要記錄插入父節點,這樣才能做插入操作
-
二叉搜索樹中的刪除操作(opens new window)
- 遞歸:前序,想清楚刪除非葉子節點的情況
- 迭代:有序遍歷,較復雜
-
修剪二叉搜索樹(opens new window)
- 遞歸:前序,通過遞歸函數返回值刪除節點
- 迭代:有序遍歷,較復雜
-
構造二叉搜索樹(opens new window)
- 遞歸:前序,數組中間節點分割
- 迭代:較復雜,通過三個隊列來模擬
#階段總結
大家以上題目都做過了,也一定要看如下階段小結。
每周小結都會對大家的疑問做統一解答,并且對每周的內容進行拓展和補充,所以一定要看,將細碎知識點一網打盡!
- 本周小結!(二叉樹系列一)(opens new window)
- 本周小結!(二叉樹系列二)(opens new window)
- 本周小結!(二叉樹系列三)(opens new window)
- 本周小結!(二叉樹系列四)(opens new window)
#最后總結
在二叉樹題目選擇什么遍歷順序是不少同學頭疼的事情,我們做了這么多二叉樹的題目了,Carl給大家大體分分類。
- 涉及到二叉樹的構造,無論普通二叉樹還是二叉搜索樹一定前序,都是先構造中節點。
- 求普通二叉樹的屬性,一般是后序,一般要通過遞歸函數的返回值做計算。
- 求二叉搜索樹的屬性,一定是中序了,要不白瞎了有序性了。
注意在普通二叉樹的屬性中,我用的是一般為后序,例如單純求深度就用前序,二叉樹:找所有路徑 ?**(opens new window)** 也用了前序,這是為了方便讓父節點指向子節點。
所以求普通二叉樹的屬性還是要具體問題具體分析。
二叉樹專題匯聚為一張圖:
?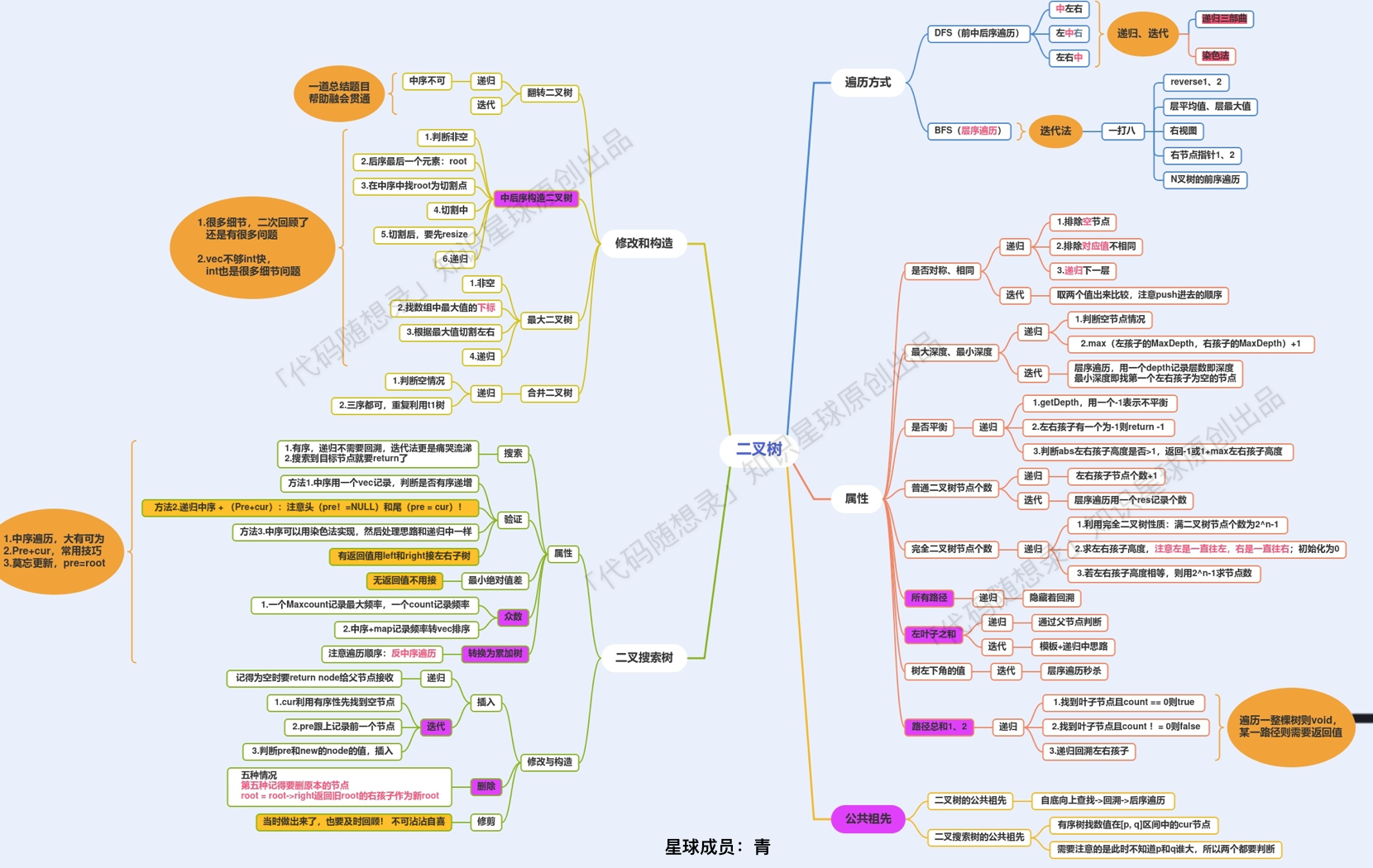 ?
?
這個圖是 代碼隨想錄知識星球 ?**(opens new window)** 成員:青 ?**(opens new window)** ,所畫,總結的非常好,分享給大家。
最后,二叉樹系列就這么完美結束了,估計這應該是最長的系列了,感謝大家33天的堅持與陪伴,接下來我們又要開始新的系列了「回溯算法」!









 方法)
![[vue] nvm](http://pic.xiahunao.cn/[vue] nvm)








