引言:本篇博客將詳細介紹到數據結構中的又一位大將——二叉樹。它也是我們目前學到的第一個非線性的數據結構。并且本章將學到的概念居多,希望大家可以理解并牢記。
更多有關C語言和數據結構知識詳解可前往個人主頁:計信貓
目錄
一,樹
1,樹的概念
2,樹的定義
二,二叉樹
1,二叉樹的概念
2,特殊的二叉樹
Ⅰ ,滿二叉樹
Ⅱ,完全二叉樹
3,二叉樹的儲存
三,結語
一,樹
1,樹的概念
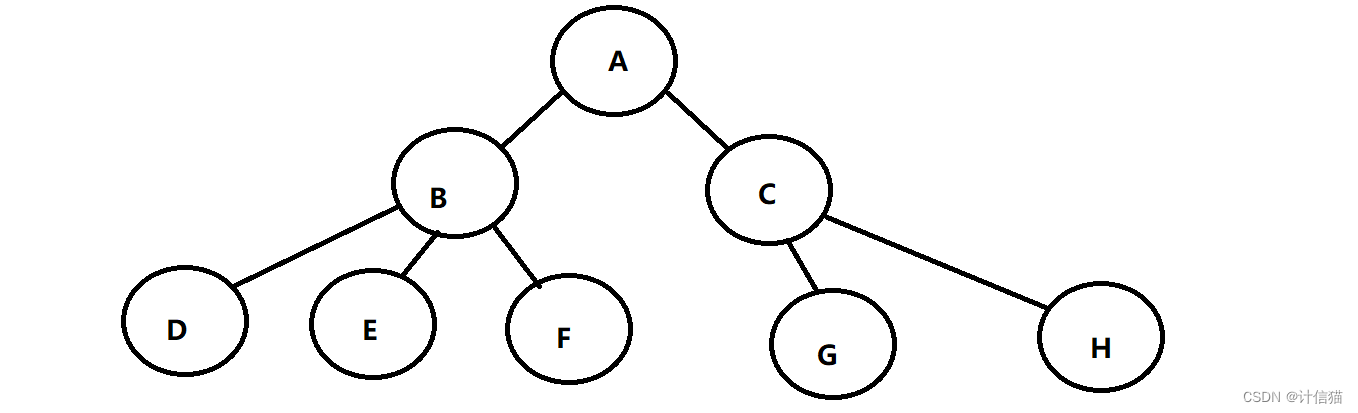
? ? ? ? 樹是一種非線性的數據結構,它由n(n>=0)個有限節點組成一個具有層次關系的集合。而在形式上就像一個倒掛的樹,根在上,葉在下。如下圖,就是一棵樹:
? ? ? ? 想要真正的了解一棵樹,那我們還應該繼續掌握關于樹的細枝末節的概念知識。?
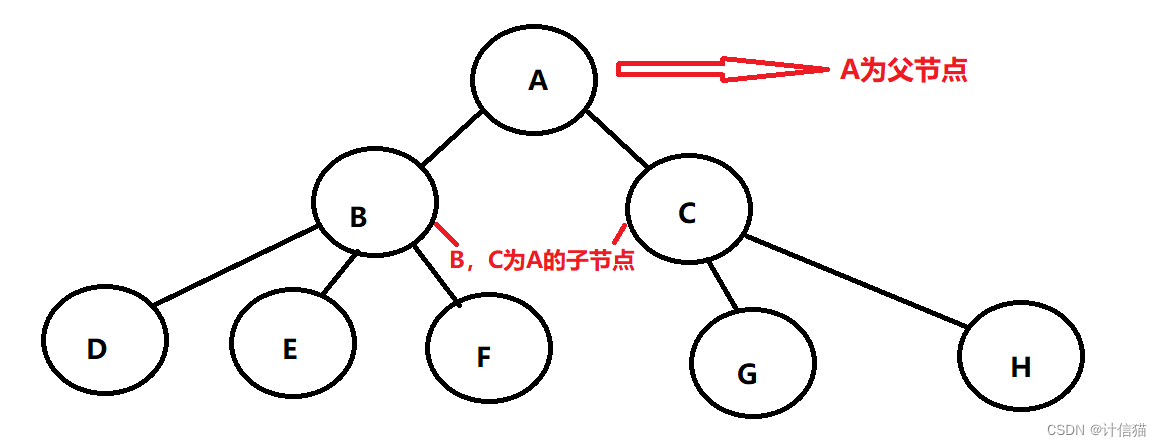
父節點/雙親節點? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?子節點/孩子節點
節點的度:某節點所含有的子節點的個數。例如A的度就為2
兄弟節點:具有相同父節點的節點。如B,C就為兄弟節點
葉節點/終端節點:無子節點,度為0的節點。如D,E,F,G,H
堂兄弟節點:父節點處于同一層上的節點。
樹的度:樹所包含的節點中的度的最大值。例如這棵樹的度就為3
樹的高度:樹的最大層次(深度)。例如這棵樹的高度就為3
森林:互不相交的樹的集合。
? ? ? ? 當然,我們也會遇到兩棵比較特殊的樹,如下:
?此時空樹的度和高度就為0,只有根節點的樹的度和高度就為1。
? ? ? ? 想要成為一棵樹,也需要同時遵守以下規則:
1,子樹之間便可以有相連或者相交的情況出現。
2,除了根節點以外,每一個節點有且僅有一個父節點。
2,樹的定義
? ? ? ??對于樹的定義,則存在一個難點,那就是一個節點的子節點的個數不確定性,導致我們不知道該定義多少個指針變量合適。
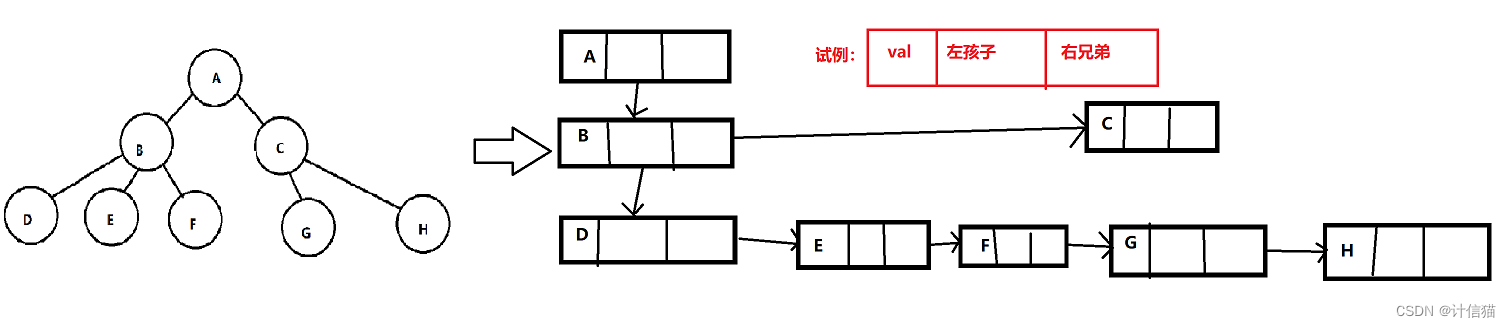
? ? ? ? 但是,我們可以使用一個方法,叫做左孩子右兄弟定義法來完美地解決這個問題。于是我們如下代碼定義一個樹:
struct TreeNode
{int val;struct TreeNode* LeftChild;//左孩子struct TreeNode* RightBrother;//右兄弟
};? ? ? ? 所以有了這個方法,我們就可以很輕松地將如下的樹使用代碼進行表示了。
? ? ? ? 而在使用此方法時,我們必須確保左孩子一定是每一層最左邊的那一個。于是我們便可以使用如下代碼來遍歷一棵樹的某一層。
struct TreeNode*cur=parent->LeftChild;//parent表示根節點
while(cur)
{//……cur=cur->RightBrother;
}二,二叉樹
1,二叉樹的概念
? ? ? ? 二叉樹無非本質上就首先是一棵樹,所以它擁有樹的全部概念。其次二叉樹的特殊之處就是二叉樹的度為2,也就是說一個節點的子節點數不可以超過2。
那么如下,就是一棵二叉樹:
? ? ???
2,特殊的二叉樹
Ⅰ ,滿二叉樹
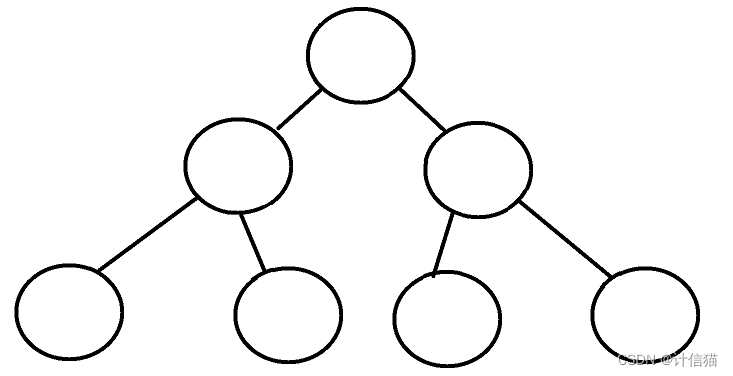
? ? ? ? 滿二叉樹的定義就是除了葉節點之外,每一個節點都達到含有了兩個子節點的二叉樹。如下圖所示:
? ? ? ? 倘若滿二叉樹的高度為H,那么我們便可以計算出它的節點個數:
Ⅱ,完全二叉樹
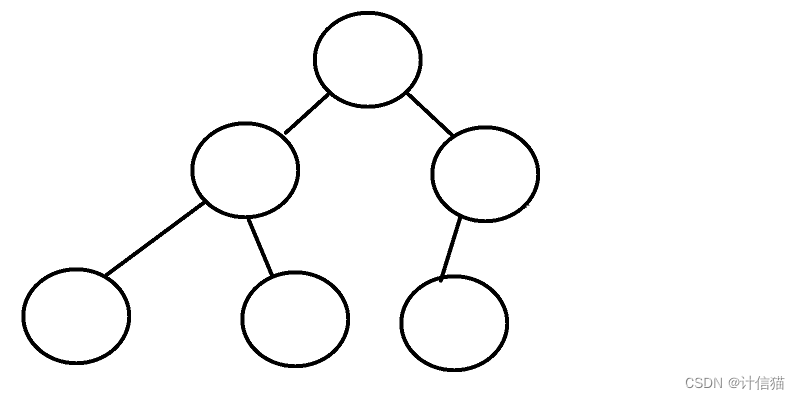
? ? ? ? 完全二叉樹則要求,前H-1層為滿二叉樹,最后一層的葉節點從左向右連續。如下圖所示:
? ? ? ? 而所要求的”連續“的意思其實就是從左到右必須葉節點緊挨著葉節點,不可以有空出來的位置。
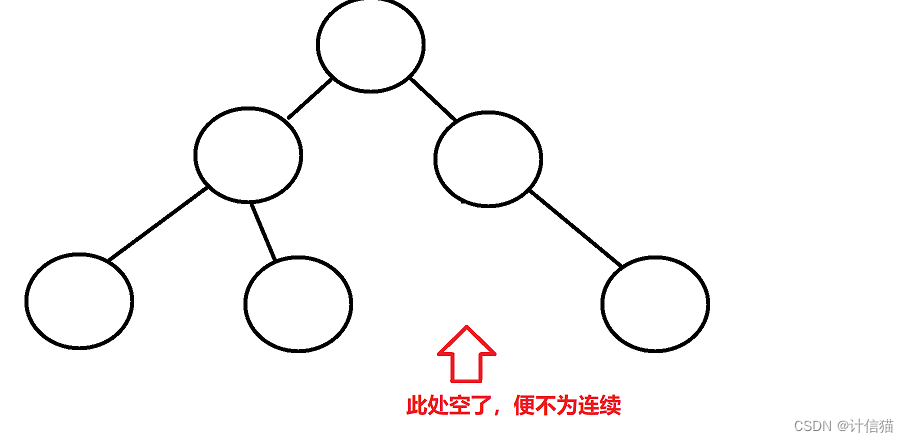
那我們舉出如下反例,便不是完全二叉樹:
3,二叉樹的儲存
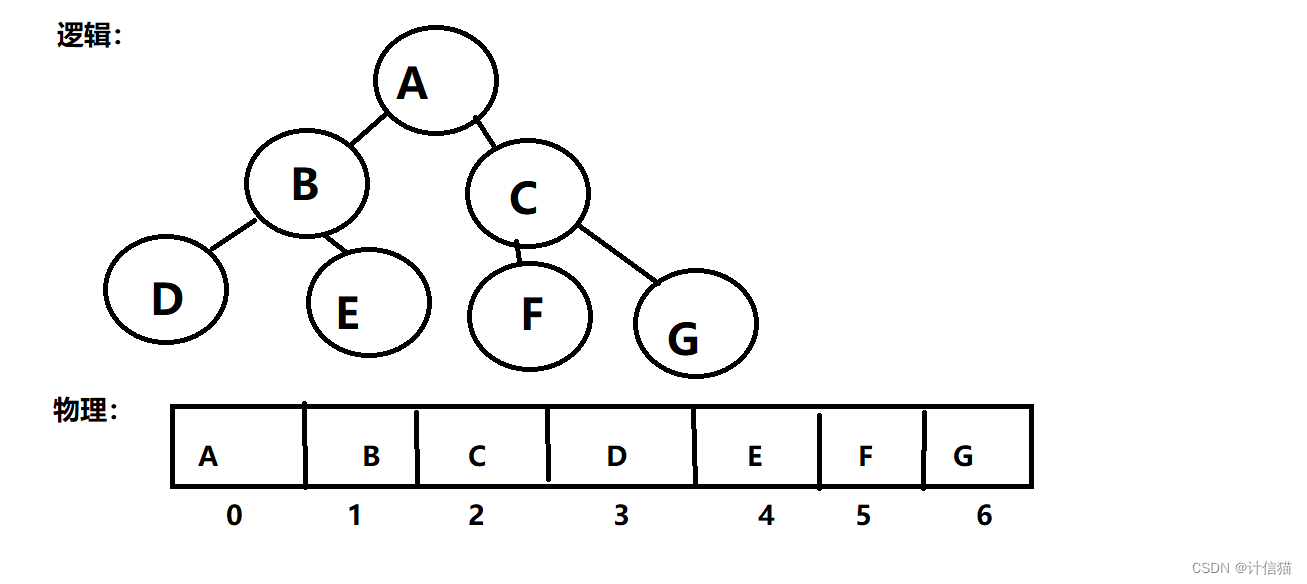
? ? ? ? 對于二叉樹的儲存,我們便是將邏輯結構與物理結構進行分離儲存。
邏輯結構:樹狀結構? ? ? ? ? ? ??
物理結構:數組結構
? ? ? ? 利用數組儲存二叉樹數據的好處就是我們可以使用下標找到某個節點的父節點或者子節點。?
通過下標尋找父/子節點
假設父節點的下標為i:左孩子節點的下標為2*i+1,右孩子節點下標為2*i+2。
假設子節點的下標為j:不管j為奇數或者偶數,其父節點的下標都為(j-2)/2——因為會涉及到int類型取整操作。
注意:若為非完全二叉樹,則不存在的節點一定要在數組中空出來,不然會導致使用下標尋找父子節點的方法失效。
三,結語
? ? ? ? 這一篇文章也僅僅只是講到了二叉樹的概念而已,接下來我會盡快更新出二叉樹數據結構的應用——堆。
? ? ? ? 而堆相較于我們以前學到的數據結構就更加的復雜難懂了,如果想要看懂堆,那么將這篇博客所講到的知識點,尤其是父子節點下標的尋找爛熟于心就是非常重要的了。希望我們可以一起克服我們所遇到的困難,一起加油!











)









