在上一節中，使用了靜態模型，我們推導出了卡爾曼濾波的狀態更新方程，但是在實際情況下，系統都是動態，預測階段，前后時刻的狀態是改變的，此時我們引入預測方程，也叫狀態外推方程；

同樣的我們通過一個例子來分析，在開始為什么要選擇卡爾曼濾波時，提出了一個例子；

在一維空間內使用雷達來追蹤勻速飛行的飛行器，此時系統狀態為飛行器的航程，速度是相對于時間的變化率，也就是距離的導數；

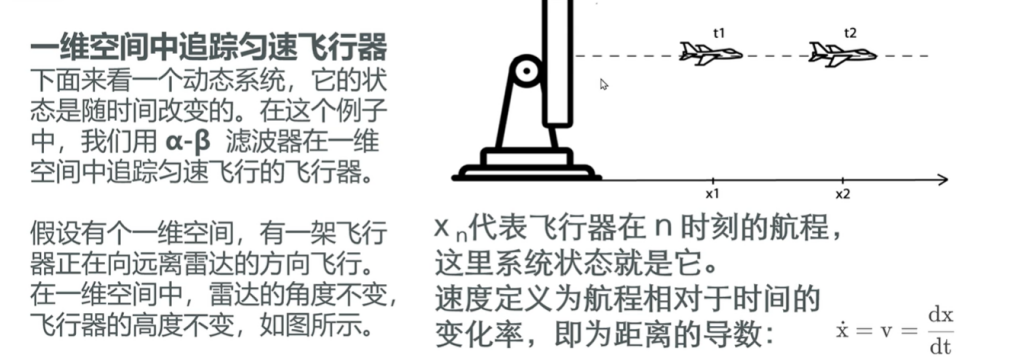
通過分析飛行器的一維物理模型，可以得到，速度恒定時，航程等于當前時刻的的航程加上時間變化*速度（距離的導數） ；

?得到的動態模型，我們稱為狀態外推方程或者預測方程；

具體化這個例子：

對于存在問題，我們分析得到兩種情況：一個是雷達的誤差，另外就是飛行器速度改變了；假設雷達的精度是20m，此時的誤差更可能是由于飛行器速度發生了改變，那么此時我們更信任雷達的測試結果，所以我們將系數調高（當系數β=1時，估計值結果=測量值）；

?假設雷達的精度是150m，此時的誤差更可能是由于雷達誤差結果，那么此時我們更信任飛機速度變化，所以我們將系數調低（當系數β=0時，估計值結果=先驗估計值）；

?具體流程：根據分析，我們設置權重因子，開始第0次迭代，首先依然是初始化，輸入估計值，與上一個例子不同是，此時我們是動態模型，預測后，先驗估計值與輸入值是不同的；

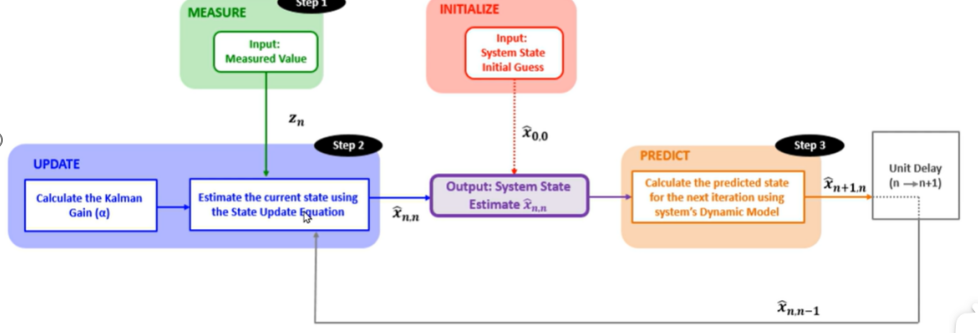
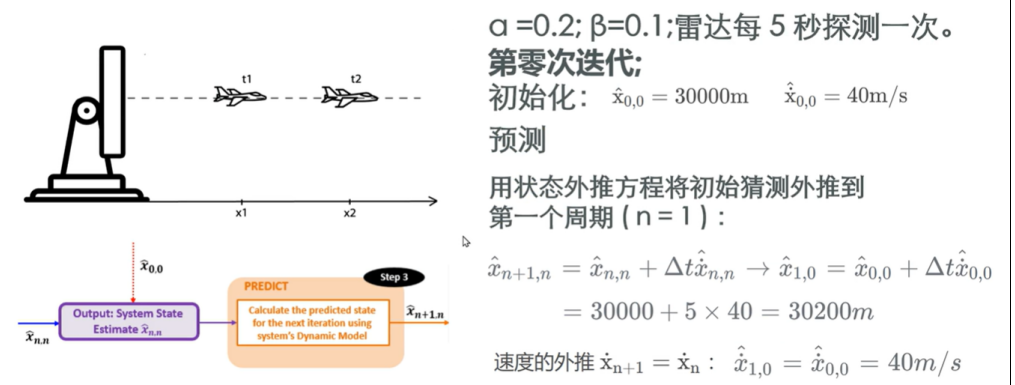
將預測的結果作為輸入給到狀態更新方程，同時輸入測量值，通過狀態更新方程計算當前估計值；

?

繼續預測下一刻的先驗估計值；?

?

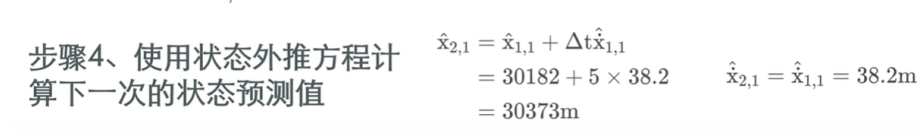不斷迭代:最終我們得到結果

?

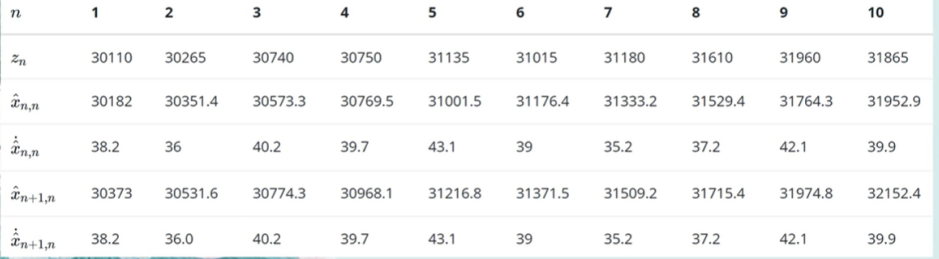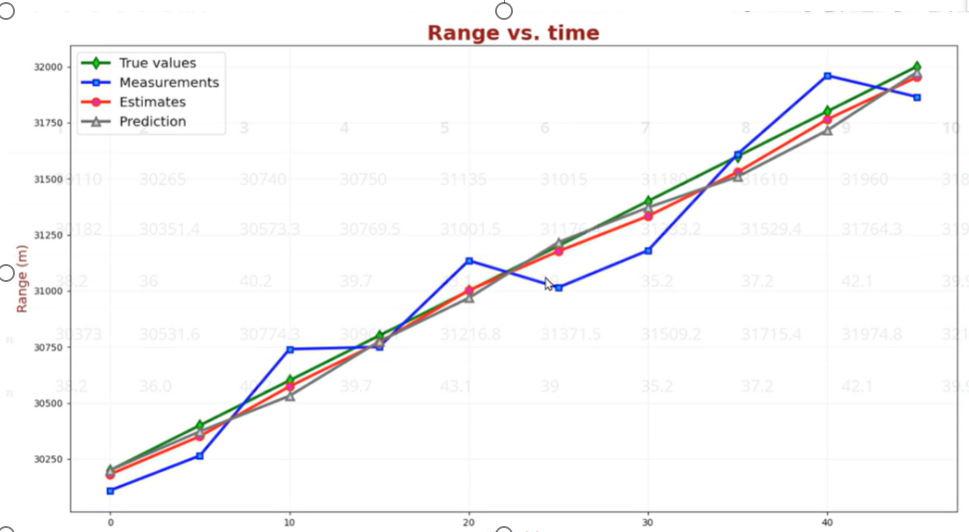
?我們可以看出，可以看到估計算法對估計結果有平滑作用，并且估計結果趨近真實值。

嘗試改變權重因子：

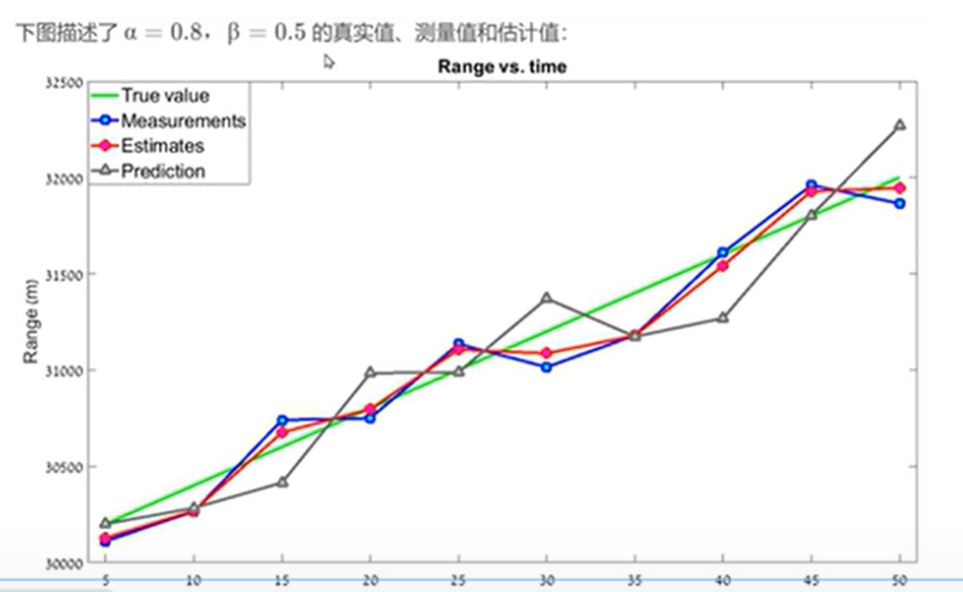
結果并不理，所以濾波器系數的選擇是至關重要的；

濾波器系數的選擇：

對于這個案例，系統狀態為航程情況下，動態改變的除了速度還可能有加速度，例如現在來一架戰斗機，它先以50m/s 的恒定速度飛行 15 秒然后以 8 m/s2 的加速度勻加速飛行 35秒。入圖顯示了目標航程、速度、加速度隨時間的變化。此時α-β兩個系數將不能滿足我們的需求，依然使用該濾波器，分析：

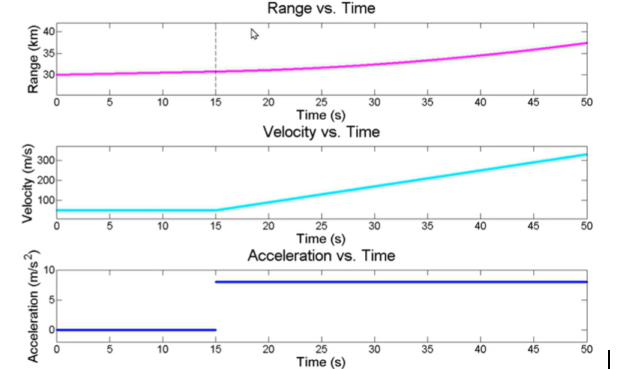
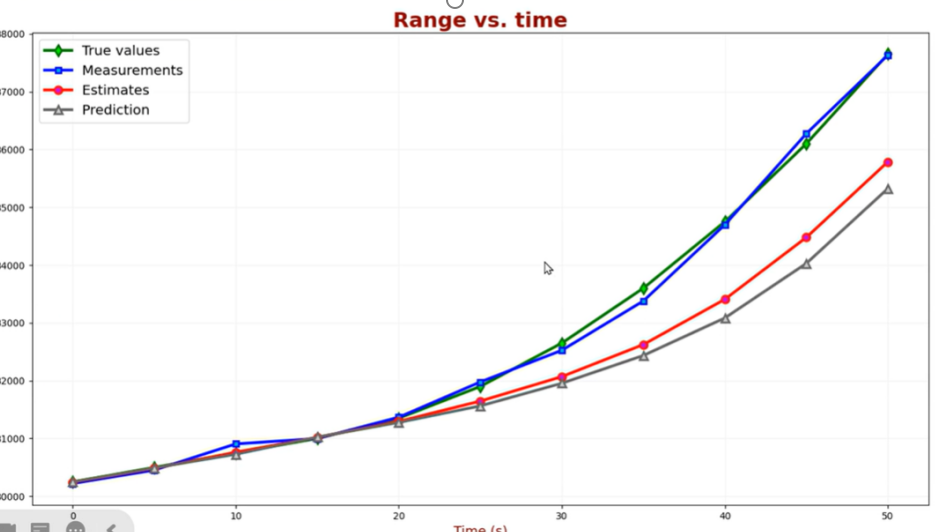
會發現，誤差非常大：

?現在使用α-β-Γ濾波器來追蹤：

根據動力學分析，此時的系統狀態外推方程：

?

?

最終得到結果：航程的擬合還是不錯的；

?

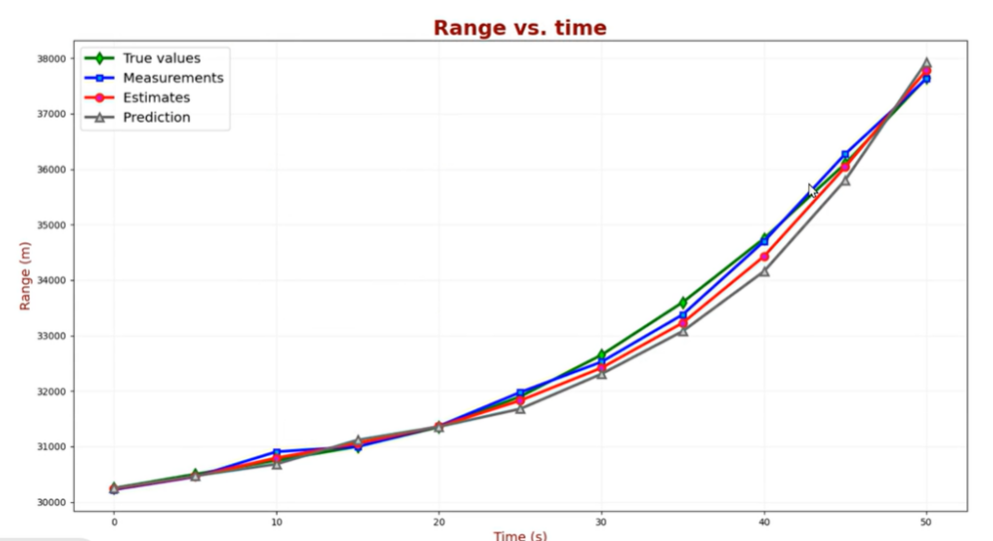?但是速度和加速度的擬合效果并不好：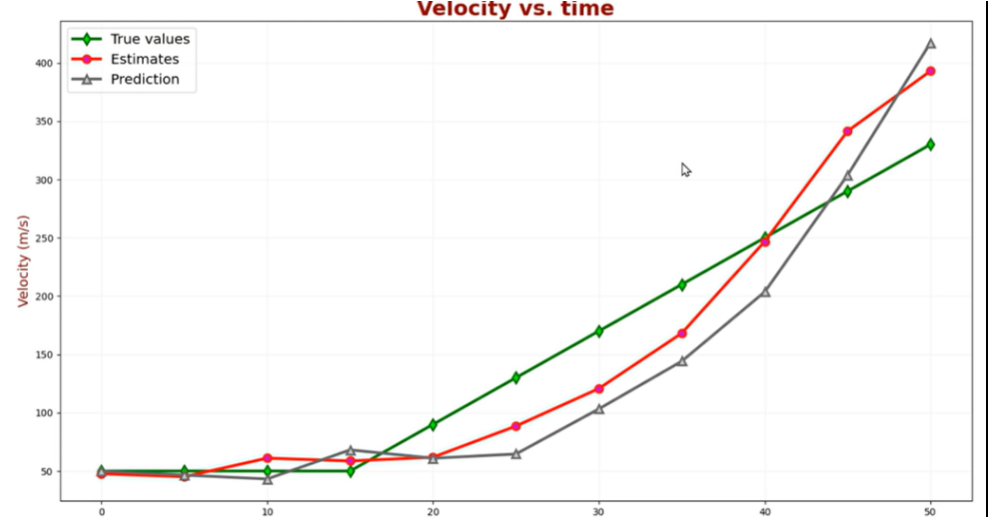

?

?

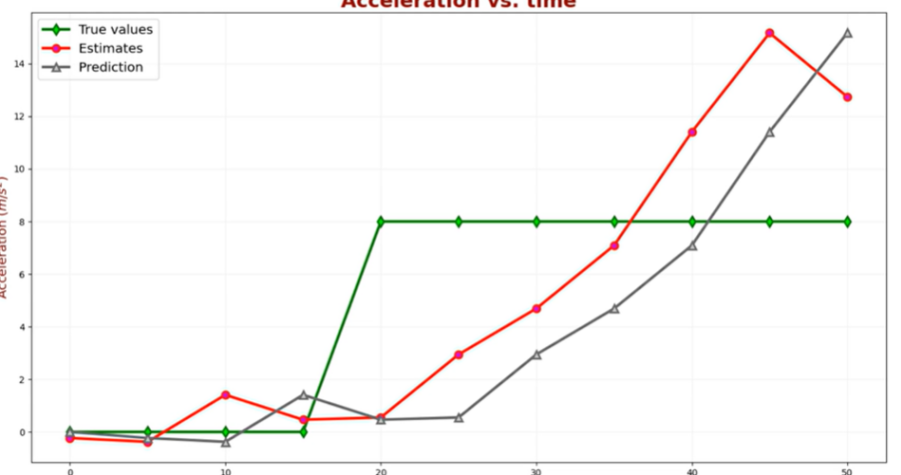?卡爾曼濾波器就可以處理動態情況下的問題；

總結:

卡爾曼濾波的第一個方程：通過先驗估計值和對殘差的權重求和得到當前估計值；

卡爾曼濾波的第二個方程：通過動態模型，得到狀態外推方程，去求得先驗估計值；